汽車爆胎對運動狀態的影響研究

周 鵬，王旭飛，劉怡帆，王鵬輝

汽車爆胎對運動狀態的影響研究

周 鵬，王旭飛*，劉怡帆，王鵬輝

（陜西理工大學 機械工程學院，陜西 漢中 723000）

汽車爆胎是一種極其危險的工況，通過數學公式難以準確表達爆胎輪胎的力學特性，試驗研究難度較大。文章以Carsim軟件中的205/45 R17型輪胎為載體，通過對爆胎輪胎參數進行修正，建立了Carsim內置輪胎爆胎模型。通過仿真計算，車輛發生爆胎會導致汽車偏離預期道路，車身向爆胎輪胎側偏轉，爆胎輪胎縱向力及側偏力劇烈變化，導致受爆胎影響最大的輪胎縱向力變大3.5倍，側偏力變大10.5倍，仿真結果為爆胎車輛穩定性控制研究提供了基礎。

Carsim；爆胎模型；運動狀態

前言

汽車爆胎的主要原因有胎壓異常、輪胎磨損等，也有行駛環境等外部原因。由于進行實車爆胎實驗的成本大且危險系數高，所以國內外學者通過對已經進行的爆胎實驗展開分析，對爆胎車輛進行計算機建模以研究汽車爆胎后的輪胎特性的變化和整車的運動軌跡。

2016年吉林大學的高元偉等人采用基于Pacej- ka89魔術公式的輪胎模型，對模型剛度進行修正得出爆胎模型，并進行了仿真實驗[1]。2019年桂林電子科技大學的劉維等人利用 UniTire 理論建立爆胎輪胎模型，并針對爆胎工況對整車影響進行了仿真實驗[2]。2020年Sathishkumar等人對卡車進行爆胎工況的仿真試驗，分析了爆胎車輛的獨立被動懸架、帶ARB （防側傾桿）的被動懸架、滾動互聯和獨立主動懸架等系統對整車運動狀態的影響[3]。

類似魔術公式輪胎模型及UniTire輪胎模型等經驗或半經驗輪胎模型，實際是對輪胎力學特性進行大量的數據分析，再通過含參數擬合的公式進行表達。在汽車正常行駛時可以較好地表達輪胎的狀態，但針對車輛爆胎工況這種緊急狀態無法進行非常準確的表述。

本文采用對Carsim 仿真軟件中的輪胎模型進行參數修正的方法，使修改過后的爆胎輪胎模型達到貼合真實的爆胎工況下的輪胎力學特性。

1 爆胎工況的簡化

車輛發生爆胎工況時，持續時間非常短暫，輪胎的力學參數與胎壓的關系難以確定，為簡化研究，假設輪胎力學參數在爆胎的過程中隨時間呈線性變化。

爆胎工況涉及到前輪后輪以及是否轉向的工況，也有單車輪或多車輪爆胎的情況，但多車輪同時爆胎的現象很少，并且多車輪一起爆胎時，輪胎爆胎的過程及參數變化范圍也都是不同的，如果討論多車輪同時爆胎只會把研究的內容復雜化且意義不大[4]。因此在本文中，爆胎工況只考慮某一車輪發生爆胎的情況。

2 內置輪胎爆胎模型

在Carsim中選擇C-Class，Hatchback 2012進行研究，四條輪胎均選擇205/45 R17型輪胎。

圖1 Carsim中205/45 R17型輪胎模型

車輛發生爆胎工況后，爆胎輪胎的力學特性會發生很大的變化，產生變化的參數主要包括：側偏剛度、外傾剛度、徑向剛度、縱滑剛度、滾動阻力系數、回正力矩、有效滾動半徑等[5]。將爆胎后輪胎參數變化的規律進行整理，見表1。

表1 爆胎輪胎參數變化

參數變化程度經歷時間/s 輪胎滾動阻力系數增大30倍0.1 輪胎有效滾動半徑70% 輪胎徑向剛度6.7% 輪胎縱滑剛度28% 輪胎側偏剛度25% 輪胎側傾剛度66% 回正力矩增大10 倍

2.1 輪胎滾動阻力的變化

輪胎在汽車行駛時做滾動運動，受壓產生形變后又恢復原狀，但由于輪胎內部存在摩擦會產生彈性遲滯損失，進而產生阻礙車輪滾動的阻力矩[6]。

爆胎后，輪胎滾動阻力系數增大到原來的30倍；正常輪胎滾動阻力常數R_C、R_V分別為0.004 和0.000 025 h/km；爆胎R_C、R_V的參數變為0.12 和0.00 075 h/km。

2.2 輪胎有效滾動半徑的變化

在CarSim中直接設置爆胎前后車輪的有效滾動半徑，輪胎發生爆胎后其有效滾動半徑降為原來的70%；正常輪胎有效滾動半徑為298 mm，爆胎后其有效輪胎滾動半徑R變為208.6 mm。

2.3 輪胎徑向剛度的變化

爆胎輪胎的徑向變形由輪胎的徑向剛度決定。爆胎后，輪胎徑向剛度變為正常值的6.7%。205/45 R17型輪胎的徑向剛度為242 N/mm，爆胎后徑向剛度變為16.214 N/mm。

2.4 輪胎縱滑剛度的變化

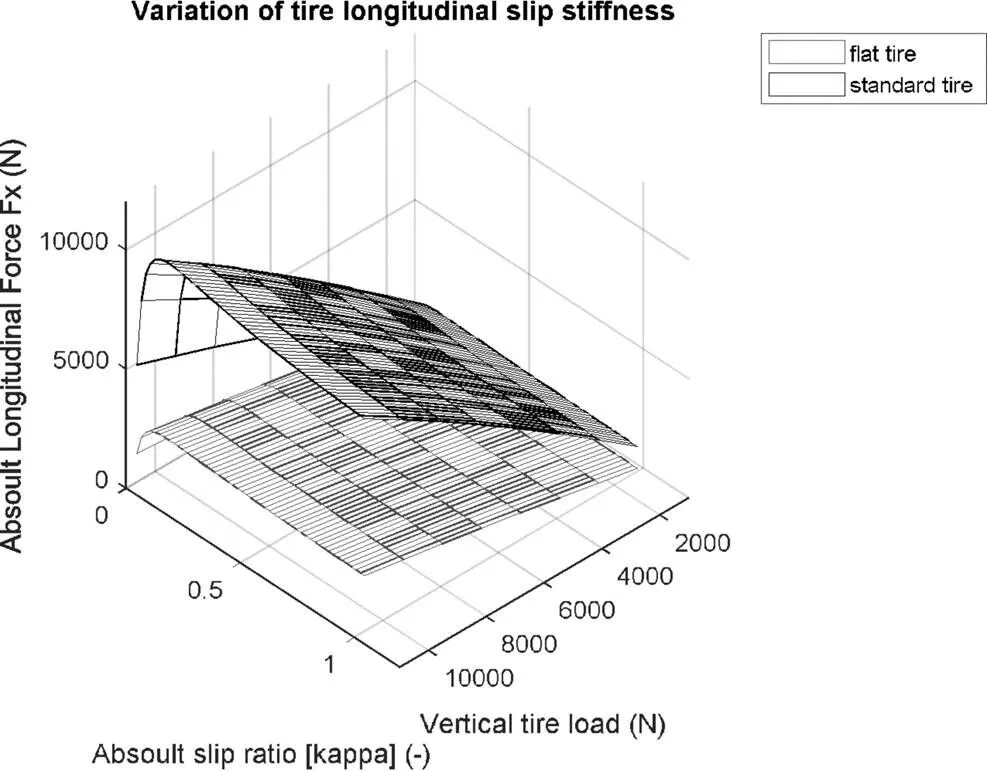
圖2 爆胎輪胎與正常輪胎縱滑剛度 Map 圖對比

爆胎后，爆胎輪胎的縱滑剛度減小為正常值的28%。如圖2所示，紅色為爆胎輪胎縱滑剛度的Map圖，黑色為正常輪胎縱滑剛度的Map圖。

2.5 輪胎側偏剛度的變化

爆胎后，輪胎的偏側剛度減小為正常值的25%。如圖3所示，紅色為爆胎輪胎偏側剛度的Map圖，黑色為正常輪胎偏側剛度的Map圖。

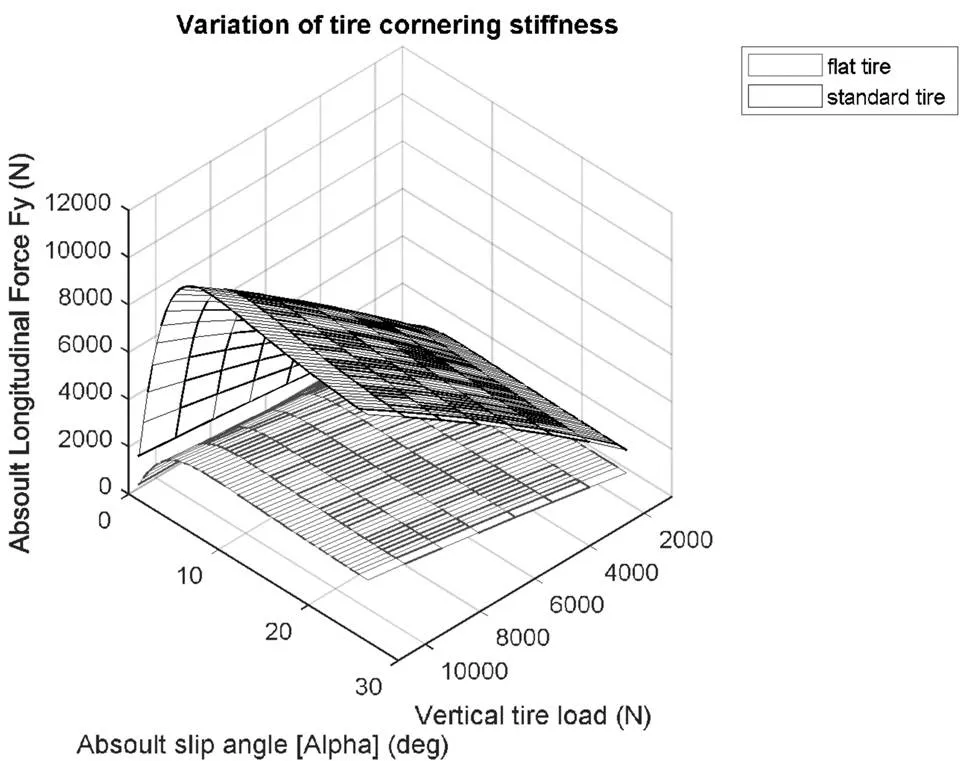
圖3 爆胎輪胎與正常輪胎側偏剛度Map圖對比

2.6 輪胎側傾剛度的變化

爆胎后，側傾剛度減小為正常值的66%。如圖4所示，黑色曲線為正常輪胎的側傾剛度系數隨垂直載荷變化的曲線，紅色曲線為爆胎輪胎的側傾剛度系數隨垂直載荷變化的曲線。

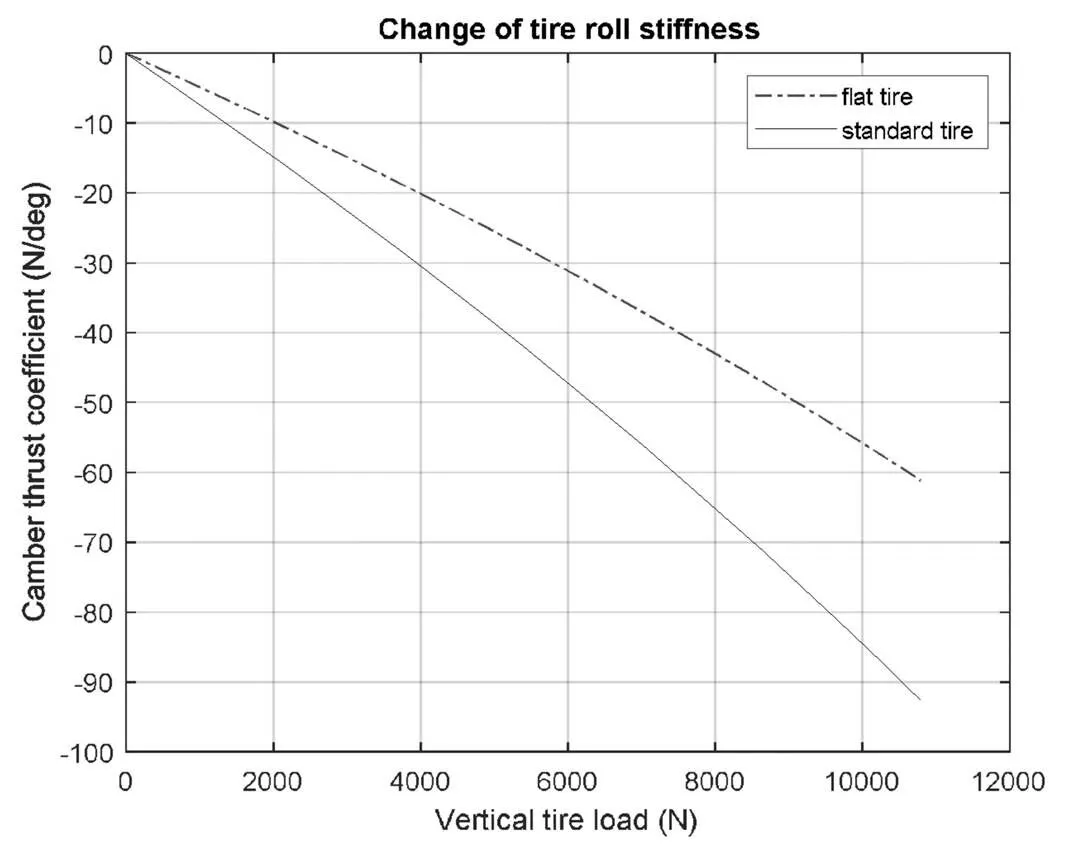
圖4 爆胎輪胎與正常輪胎側傾剛度對比

2.7 輪胎回正力矩的變化

爆胎后，回正力矩增大為正常值的10倍。如圖5所示，紅色為爆胎輪胎回正力矩的Map圖，黑色為正常輪胎回正力矩的Map圖。

圖5 爆胎輪胎與正常輪胎回正力矩 Map 圖對比

3 仿真結果分析

車輛爆胎仿真模型設置為左前輪發生爆胎，車速為120 km/h，地面附著系數為0.85，仿真時間為10 s。仿真結果如圖6—圖13所示：

圖6 車輛側向位移

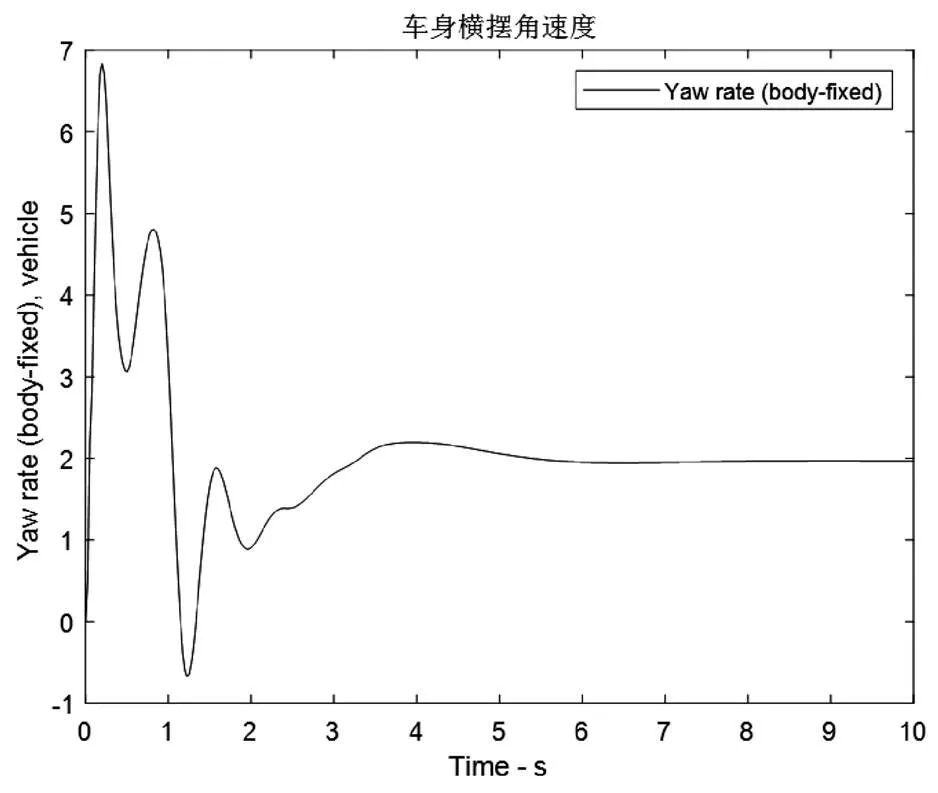
圖7 車身橫擺角速度

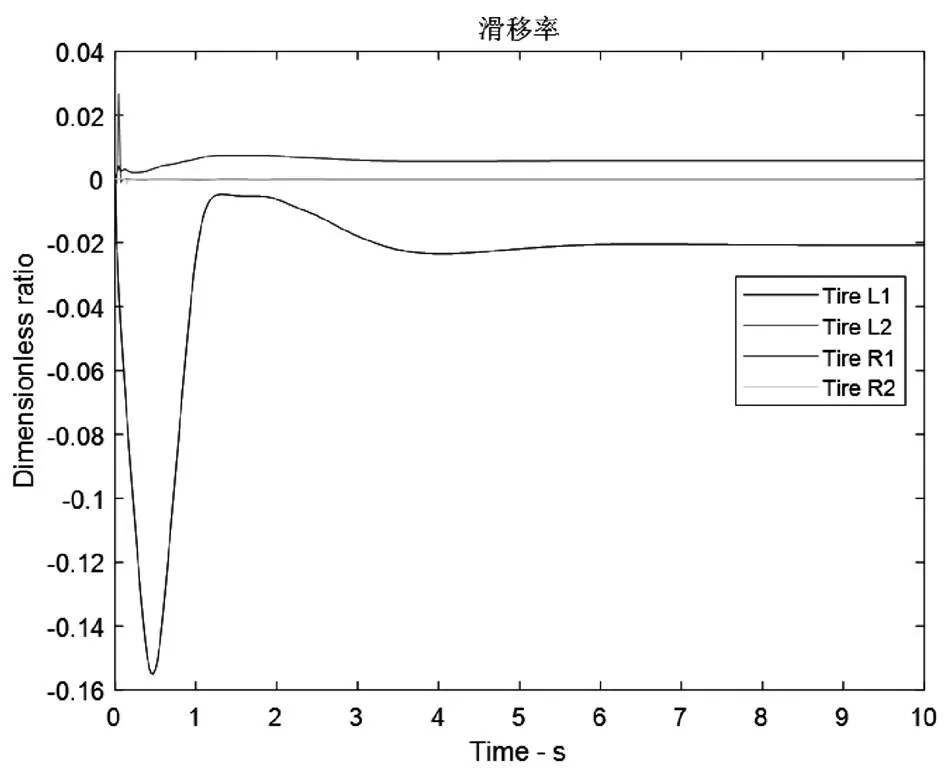
圖8 滑移率

圖9 輪胎縱向力

圖10 側偏角

由圖6可知，車輛在爆胎后，且在不施加控制的情況下，輪胎的有效滾動半徑會迅速減小到正常值的70%，導致側偏位移相當大，10 s內偏離車道約60 m。在爆胎工況發生后約2 s就能沖出本車道，甚至能撞到道路旁的護欄或者樹木。

由圖7可知，在汽車發生爆胎瞬間，車身橫擺角速度劇烈增大，1 s內峰值能達到6.8 rad/s，說明車輛處于嚴重失控狀態，甚至發生測滑或者甩尾等危險工況；由于慣性作用，在1.25 s時，車身橫擺角速度達到最低值－0.7 rad/s；在發生震蕩后，于5.5 s時，橫擺角速度達到2.0 rad/s這一穩定值，說明汽車還在繞垂直軸發生偏轉，相當于汽車以一個固定角度進行轉彎，但依舊處于不穩定狀態。

由圖8可知，在汽車發生爆胎瞬間, 爆胎輪胎的滑移率劇烈增大，在1 s內峰值達到－0.155即15.5%，說明此時爆胎輪抗側滑能力迅速下降，極易失控；由于慣性作用，在發生震蕩后，于5.5 s時趨向穩定，達到－0.021即2.1%。

由圖9可知，在汽車發生爆胎瞬間，爆胎輪胎的縱向力急劇增大，在0.1 s時達到峰值－800N，隨后由于慣性作用產生振蕩，在1.25 s時達到最大值約－118 N，并于5.5 s時趨于穩定，達到－405 N。同時爆胎后，左前爆胎輪會對右前輪的縱向力產生較大影響，使右前輪的縱向力于1.25 s時達到峰值約為1 075 N，在震蕩后于5.5 s時趨于一個穩定值885 N，比正常行駛時的縱向力（250 N）大了3.5倍。

由圖10可知，在汽車發生爆胎后，四個輪胎的側偏角都發生較大的變化，說明此時車輛產生了側偏。爆胎輪的輪胎側偏角變化最大，于0.5 s時達到峰值－1.2 deg，于5.5 s時趨于－0.55 deg。其余輪胎都隨著爆胎輪發生變化，幅度較小。

圖11 輪胎側偏力

由圖11可知，在汽車發生爆胎后，四個輪胎的側偏力產生了不同的變化。爆胎輪由于與地面接觸增加，導致側偏力變化不明顯，于0.95 s時達到峰值265 N，并于6 s時趨于穩定達到208 N。右前輪受爆胎輪的影響變化巨大，于0.5 s達到峰值1 845 N，隨后受慣性作用達到最小值140 N，最終于6 s時趨于穩定值630 N，比正常行駛時的側偏力（60 N）大了10.5倍。左后輪受爆胎輪的影響變化較大，于0.5 s達到峰值1 010 N，隨后受慣性作用達到最小值160 N，最終于6 s時趨于穩定值540 N，符合爆胎車輛的偏側特性。

圖12 外傾角

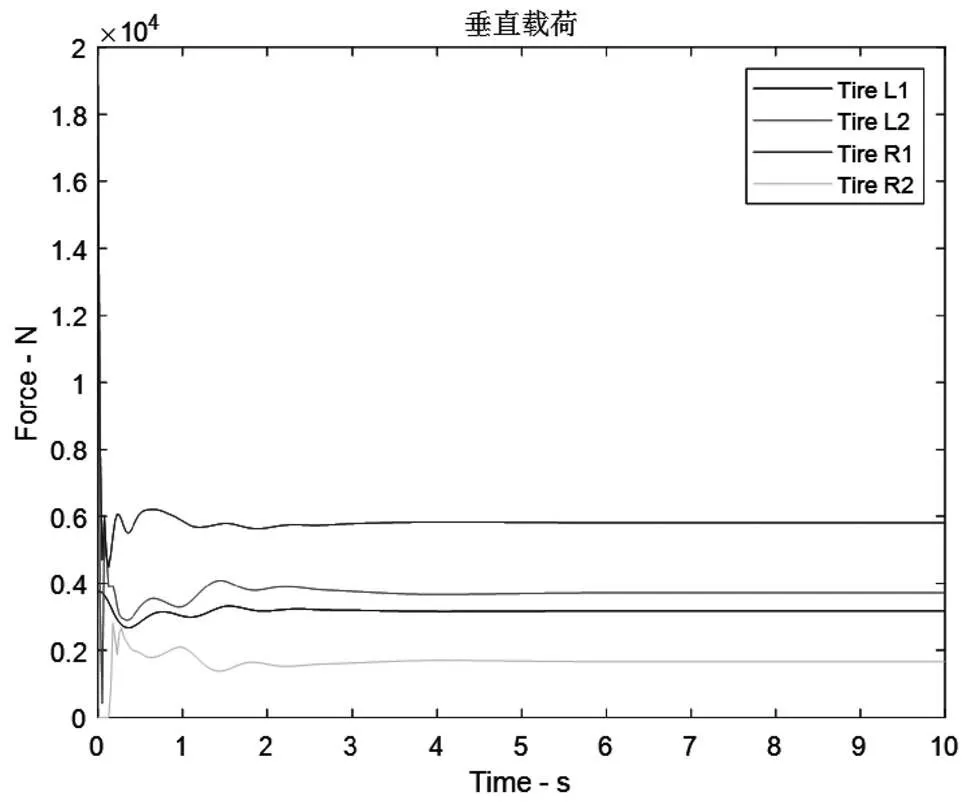
圖13 垂直載荷

由圖12可知，在汽車發生爆胎后，輪胎外傾角變化幅度較大。爆胎輪及右前輪的外傾角穩定后分別達到－3.0 deg和－2.7 deg，證明此時輪胎內側產生單邊磨損，懸掛系統零件磨損加速，車輛正朝左一側跑偏。

由圖13可知，在汽車發生爆胎后，輪胎垂直載荷變化巨大。爆胎輪的垂直載荷減小，穩定后達到3 180 N；右前輪及左后輪的垂直載荷增大，在爆胎的一瞬間，右前輪的垂直載荷達到峰值18 850 N，有可能引起新的爆胎工況發生，在2 s后右前輪及左后輪的垂直載荷趨于穩定，分別達到5 800 N和3 700 N；右后輪受爆胎輪影響，在2 s后達到穩定值1 700 N。符合爆胎車輛的垂直載荷變化特征，即車輛發生爆胎工況后，爆胎輪以及對角車輪的垂直載荷將會減小，而另一對角線的兩個車輪的垂直載荷將會增大。

對比文獻[2]、[4]，選用的輪胎型號和建模方式略有不同，仿真結果也存在一些偏差，主要集中在橫擺角速度、車輛側向位移、輪胎縱向力及滑移率等方面。本文橫擺角速度變化處于－0.7 rad/s～7 rad/s之間，對比文獻[4]所述橫擺角速度變化處于－0.02 rad/s～0.02 rad /s之間（汽車行駛方向發生的偏轉量極小），從爆胎后整車的運動狀態會發生很大變化來看比較符合實際情況。車輛發生爆胎后，當車速達到120 km/h時，左前轉向輪爆胎后在不施加控制的情況下，由于輪胎半徑發生巨大變化，在慣性作用下，車輛在5 s內的側向位移應發生很大的變化，文獻[2]的車輛側向位移在爆胎發生后5 s時處于20 m內。對比文獻[4]，在爆胎后的輪胎縱向力及滑移率的仿真結果表明四條輪胎之間的變化關系明顯區分且變化范圍也比較合理。

4 結語

通過對爆胎輪胎的建模仿真，可以得到符合實際的爆胎車輛行駛狀態和力學特性的變化。爆胎會導致汽車偏離預期道路，車身向爆胎車輪側偏轉，爆胎輪胎的滑移率、側偏角劇烈增大，縱向力劇烈波動，四條輪胎的側偏角都會產生較大波動，但爆胎輪的側偏力沒有太大波動，外傾角變化較小，垂直載荷相應減小。同時左前輪胎爆胎會影響右前輪胎的縱向力、側偏力、垂直載荷發生劇烈變化。所以本研究，對避免爆胎造成新的危險發生具有一定的實際意義，也為后續的爆胎車輛穩定性控制研究奠定了一定的基礎。

[1] 高元偉.駕駛員干預下的爆胎動力學建模及仿真分析[D].長春:吉林大學,2016.

[2] 劉維,張向文.爆胎汽車穩定性控制的模糊滑模控制算法研究[J].機械科學與技術,2019,38(12):1944-1953.

[3] Sathishkumar P, Wang R, Yang L, et al. Trajectory control for tire burst vehicle using the standalone and roll interconnec- ted active suspensions with safety-comfort control strategy [J].Mechanical Systems and Signal Processing,2020,142: 106776.

[4] 史昀珂.分布式驅動汽車的爆胎穩定性控制研究[D].南京:東南大學,2018.

[5] 王英麟.基于CarSim與UniTire的爆胎汽車動力學響應研究[D].長春:吉林大學,2007.

[6] 余志生.汽車理論[M].北京:清華大學出版社,2011.

Study on the Influence of Car Flat Tire on Motion State

ZHOU Peng, WANG Xufei, LIU Yifan, WANG Penghui

( School of Mechanical Engineering, Shaanxi University of Science and Technology, Shaanxi Hanzhong 723000 )

Flat tire is an extremely dangerous condition, and it is difficult to accurately express the mecha- nical properties of tire with tire explosion through mathematical formula, so it is difficult to conduct experimental research. In this paper, the 205/45 R17 tire in Carsim software is taken as the carrier, and the flat tire model is established by modifying the tire parameters. Through the simulation calculation, the car body will deviate from the expected road when the tire blows out, and the longitudinal force and lateral force of the tire change dramatically. The longitudinal force of the tire most affected by the falt tire will increase 3.5 times, and the lateral force will increase 10.5 times, the simulation results provide a basis for the stability control of the vehicle with flat tire.

Carsim; Flat tire model; Motion state

U467

B

1671-7988(2022)02-82-05

U467

B

1671-7988(2022)02-82-05

10.16638/j.cnki.1671-7988.2022.002.019

周鵬，碩士研究生，就讀于陜西理工大學機械工程學院，主要研究方向：汽車動力學及控制研究。

王旭飛，副教授，碩士生導師，就職于陜西理工大學機械工程學院，主要研究方向：汽車動力學及控制研究。

陜西省重點實驗室項目（18JS020）。