機載往復密封二元時變相關退化建模與可靠度評估

柏文峰， 洪 黎， 張 超， 錢于杰

(1.中國航發控制系統研究所， 江蘇 無錫 214100； 2.北京航空航天大學 自動化科學與電氣工程學院， 北京 100191)

引言

航空工業是一個國家科技水平、工業能力和綜合國力的集中體現，液壓技術因其驅動功率密度大、快速性好、剛性大等優點，已經在航空領域得到廣泛的應用[1]。往復密封件作為機載液壓系統作動器的重要組成部分，其性能和可靠性會直接影響飛機的整體性能與安全。液壓往復密封件主要受密封耦合面的潤滑、摩擦、磨損、材料性質以及結構設計原理的影響，其中密封耦合面間的摩擦將導致密封件表面材料的喪失和遷移，導致密封件的磨損，影響其使用壽命[2]。航空液壓作動器工況復雜，壓力、溫度、作動速度、頻繁的振動、多變的載荷狀態等嚴酷的機載環境對往復密封件的性能都具有較高的要求。

國內外對于往復密封的失效機理進行了大量的理論和試驗研究。針對往復密封的理論研究，主要采用彈性方程和流體雷諾方程。SALANT R F等[3]利用正向求解雷諾方程的方法建立活塞桿往復密封的數值模型。歐陽小平等[4]通過求解考慮空化及流動因子的雷諾方程，建立了基于混合潤滑理論的往復密封多場耦合模型。國內對于往復密封的研究對密封件建立數值模型并進行有限元分析[5-6]，同時也進行了往復密封的試驗研究[7-9]。對于機載高壓、寬溫、強振動、變載荷等惡劣工況，單純依靠失效物理、數值迭代或工程經驗建模分析已經無法準確地描述往復密封件的實際工作情況。

近年來，基于隨機過程的退化過程建模逐漸成為了研究熱點，維納過程[10-11]、伽馬過程[12-13]和逆高斯過程[14-15]都是主流的隨機退化過程。維納過程可以靈活地描述各種系統的退化指標，且結果令人滿意，因此維納過程最近受到較多的關注。國內外大量的關于電子元件、機械元件的性能退化建模基于隨機過程方法進行研究，這對往復密封件的性能退化分析及可靠性建模提供了理論支撐。

工程實際中，機電產品不止1個性能退化指標。若僅考慮1個性能指標，退化過程建模不準確或者不精確。Copula函數因其優良的特性，已經被廣泛應用于金融、風險管理等領域。近些年來，Copula函數逐漸被學者引入可靠性評估與壽命預測領域，用于描述多個部件之間失效模式的相關性或者多個物理量之間的相關性等。ARMA表達是時間序列分析常用的模型。WANG等[16]采用ARMA(1,10)模型表征Copula函數的時變相關性系數，解決多個相關退化量之間的時變相關性問題。PAN J等[17]針對密封件貯存時2個退化量相關性分析，使用ARMA模型考慮其相關性系數隨時間變化的規律，并得到相關的可靠性信息。

綜上，為了解決高壓、寬溫、強振動、變載荷等惡劣工況條件下機載往復密封的可靠性評估難題，本研究建立基于ARMA模型的機載往復密封二元時變相關退化模型，基于維納過程分別建立往復密封的摩擦力和泄漏量的退化模型，采用Copula函數解決2個性能退化指標之間的相關性問題，采用ARMA模型表征相關性系數隨時間的變化。在模型求解時，采用2段貝葉斯參數估計的方法進行參數估計，基于馬爾可夫鏈蒙特卡洛循環(MCMC)的方法對往復密封的可靠性進行評估。

1 基于維納過程的往復密封退化模型

1.1 往復密封原理

圖1為往復密封的原理圖，密封件被安裝在特定的密封腔中，起到阻止油液泄漏的作用，在外側還安裝有防塵圈，起到輔助密封和防止外界雜質進入的作用。當活塞桿向液壓缸外側伸出(外行程)時，液壓油會被活塞桿拖拽至外部環境，造成油液泄漏及環境污染；當活塞桿向液壓缸內側收回(內行程)時，一些油液會被帶回液壓缸內，同時外部的粉塵微粒、空氣等雜質被帶入液壓缸，導致密封件的磨損以及油膜的破裂。活塞桿往返的2次軸向運動，形成1個工作循環，活塞桿表面的潤滑油膜會隨往復運動而不斷變化。

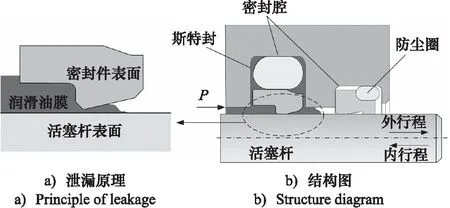
圖1 往復密封原理圖Fig.1 Principle diagram of reciprocating seal

機載往復密封件工況復雜，摩擦力、泄漏量、接觸區域溫度、磨損量等都是其性能退化指標，皆可反映往復密封件的性能退化，且互相耦合。相關研究表明，摩擦力和泄漏量是反映往復密封件狀態的最重要的2個性能退化指標。往復運動過程中，潤滑油膜不僅起到密封作用，同時也會對密封件所受摩擦力和泄漏量產生一定影響。摩擦生熱會使油膜溫度升高，油液黏度降低，泄漏量會增加，油膜承載力降低，反過來也會影響摩擦力大小。同時，摩擦力的增加也會導致密封件磨損量的增加，進而導致泄漏量的增加。由此可知，往復密封件所受摩擦力和泄漏量之間相互關聯，相互耦合，相互影響，因此考慮摩擦力與泄漏量這2個性能退化指標。

1.2 基于維納過程的往復密封退化建模

維納過程適用于因微小修復、自我修復或降低使用強度而導致的非單調退化過程。因此，基于維納過程的退化建模已經廣泛應用于機械部件、電子產品等領域的可靠性評估與壽命預測中，且取得了較為豐富的研究成果。本研究假定往復密封件的退化過程服從維納過程。

令{Xk(t)，t≥0}，表示密封件第k個性能退化指標在t時刻的退化量，其中k取1或2。假定這2個性能退化指標的退化過程服從非線性維納過程，可表示為：

{Xk(t)=μkΛk(t)+σkW(Λk(t))，t>0}

(1)

式中，μk為第k個性能退化量的漂移參數，用于描述退化速率；σk為第k個性能退化量的擴散系數，用于描述退化過程的隨機性；W(·)為標準布朗運動；Λk(t)是時間尺度變換函數，用于描述第k個性能退化量的退化軌跡。

機載工況下，往復密封件的退化過程受作動器作動距離、速度、頻率等影響。本研究進行的試驗主要針對恒定應力，因此基于維納過程建立退化模型時，退化速率μk、擴散系數σk在整個退化過程中保持不變，假設漂移參數和擴散參數的時間尺度變換函數滿足時間的冪指數關系，即Λk(t)=tqk。

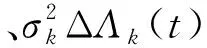
(2)

式中, ΔΛk(t)=Λk(t+Δt)-Λk(t)。

第k個性能退化指標在t時刻的退化量ΔXk(t)的分布函數Fk(ΔXk(t))滿足：

(3)

式中，Φ(·)為標準正態分布。

設Dk為密封件的第k個性能退化指標對應的失效閾值，即若Xk(t)≥Dk，則認為密封件失效，密封件壽命Tk可表示為：

Tk=inf{t,Xk(t)≥Dk}

(4)

其中，Tk的失效概率密度函數為：

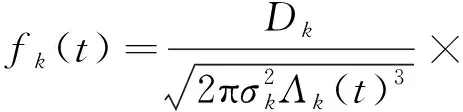
(5)

其累積分布函數為：

(6)

式中，fk(u)為Tk失效概率密度函數。

綜上可得產品的可靠度函數Rk(t)為：

Rk(t)=1-Fk(t)

(7)

若共有N個密封件進行退化試驗，Xk(tij)表示第i個密封件的第k個性能退化指標在tj時刻的退化量，退化增量為ΔXk(tij)=Xk(tij)-Xk(ti(j-1))。對于任意的第i個密封件，在互不重疊的時間區間內，2個性能退化指標的退化增量之間互相獨立；僅當在相同的時間區間內，2個性能退化指標的退化增量具有相關性，可用Copula函數來表征這種相關性。

2 往復密封二元時變相關退化模型

2.1 基于Copula函數的相關退化建模

Copula函數連接起2個邊緣分布函數，更加靈活，因此近年在可靠性領域得到了廣泛的應用。為了解決往復密封件的多個性能退化指標之間的相關性問題，采用Copula函數表示多個性能退化指標之間的相關性。

利用二元Copula函數研究摩擦力和泄漏量的相關性可分為2個階段，第一階段先分別計算摩擦力和泄漏量各自的邊緣分布函數，第二階段將摩擦力和泄漏量的邊緣分布函數作為Copula函數的輸入，由此可簡化計算。采用Frank Copula函數來表征往復密封摩擦力與泄漏量之間的相關性關系，Frank Copula函數的分布函數為：

(8)

概率密度函數為：

(9)

用Copula函數來分析第i個密封件的摩擦力和泄漏量之間的相關性，其具體形式由式(10)給出：

H(ΔX1(tij),ΔX2(tij))

=C(F1(ΔX1(tij)),F2(ΔX2(tij));θi)

(10)

式中，θi為Copula函數在描述第i個密封件的摩擦力和泄漏量之間相關性系數。考慮到不同密封件個體間的差異，每個密封件對應的相關性系數θi不同。若共有N個密封件進行退化試驗，則可得到N個Copula函數的相關性系數(θ1,θ2…,θN)[18]。

假設D1，D2分別為2個性能退化指標的閾值，任意一個退化量X1(t)或X2(t)超過各自對應的閾值時即認為失效，基于此假設往復密封件的可靠度函數R(t) 可以表示為：

R(t)=P{X1(t)≤D1,X2(t)≤D2}

(11)

2.2 基于ARMA模型的時變相關性系數建模

傳統的基于Copula函數的二元相關退化過程模型中，用以描述2個性能退化指標的相關性關系的Copula函數參數θ一般被視為常數，其表示的物理意義是該系統的2個性能退化指標之間的相關性關系不隨時間改變。在工程實際中，隨著環境與自身條件不斷改變，2個變量之間的相關性關系往往隨時間不斷變化。往復密封件在往復運動過程中，外界工況不斷變化，且密封件自身狀態也隨時間變化，因此考慮2個性能退化指標之間的時變相關性。

針對這一問題，將Copula函數的時變相關性系數用ARMA模型表達，并用常數作為對比，建立基于Copula函數的往復密封二元時變相關退化模型。假設相關性系數θ滿足ARMA(1,10)模型，其數學表達式如下：

(12)

式中,uij=F1(ΔX1(tij))，vij=F2(ΔX2(tij)),Γ(·)為轉換函數，保證參數在定義域內。

綜上所述，由式(2)、式(10)和式(12)得到基于ARMA的機載往復密封二元時變相關退化模型：

(13)

3 參數估計與可靠度評估

3.1 基于貝葉斯方法的參數估計

由Copula函數的特點可將基于ARMA的機載往復密封二元時變相關退化模型求解分為2個獨立的階段：第一階段分別求解往復密封件摩擦力、泄漏量各自的一元退化過程，對應的2個維納過程參數為α=(μ1,σ1,q1,μ2,σ2,q2)；第二階段求解往復密封件的摩擦力和泄漏量之間的時變相關性關系，對應的ARMA模型參數為θ=(ωθ,βθ,αθ)。本研究采用貝葉斯參數估計的方法進行參數估計。

上述基于ARMA模型的機載往復密封二元時變相關退化模型的對數似然函數表示為：

(14)

式(14)給出的數似然函數L(α,θ)可視為2個似然函數的相加，兩部分分別對應于模型求解的2個階段。摩擦力和泄漏量退化過程的對數似然函數和具有時變相關性系數的Copula函數的對數似然函數分別表示為：

(15)

通過式(15)，結合貝葉斯參數估計的方法可分別估計出退化過程參數α和隨機相關參數θ。

第一階段估計2個維納過程的參數α，其數學表達式如下：

P(α|ΔXk(tij))∝π(α)×L(ΔXk(tij)|α)

(16)

式中,P(α|ΔXk(tij))為后驗分布，π(α)為先驗分布，取無信息先驗分布。在得到參數α的估計值以后，結合式(3)計算摩擦力和泄漏量各自的邊緣分布函數F1(ΔX1(tij))和F2(ΔX2(tij))的值。

第二階段估計先將第一階段求得的摩擦力和泄漏量的邊緣分布函數F1(ΔX1(tij))和F2(ΔX2(tij))作為Copula函數的輸入量uij和vij，然后估計滿足ARMA模型的Copula函數時變相關性系數的參數θ，其數學表達式見式(17)：

P(θ|(uij,vij))∝π(θ)×L((uij,vij)|θ) (17)

式中,P(θ|(uij,vij))為后驗分布；π(θ)為先驗分布，取無信息先驗分布。

OpenBUGS是英國劍橋大學研究的一款貝葉斯統計分析的軟件，本研究有關貝葉斯參數估計部分將由OpenBUGS軟件計算。

3.2 可靠度評估

根據維納過程、Copula函數、ARMA模型建立的基于ARMA的機載往復密封二元時變相關退化模型，其根本目的是通過該模型計算往復密封件的可靠度，以指導實際工程應用。僅考慮1個性能退化指標時，可靠度計算較為簡單，例如對于服從維納過程的退化模型，由式(7)可得其可靠度。當有多個性能退化指標時，若多個退化量之間互相獨立，可分別計算每個退化量的可靠度；若多個退化量之間相關，則不能直接單獨計算，其可靠度計算也較為復雜。由二元相關退化模型可靠度計算的基本原理出發，采用基于馬爾可夫鏈蒙特卡洛循環的可靠度計算方法。

考慮摩擦力與泄漏量，這2個退化指標中任意1個超過其失效閾值，則判定往復密封件失效。往復密封件可靠度R(t)的物理意義是：t時刻密封件能夠正常工作的概率，即t時刻之前摩擦力與泄漏量的最大值均小于其失效閾值D1和D2的概率。

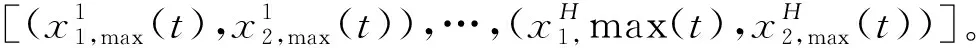
4 機載往復密封試驗裝置與模型驗證

4.1 機載往復密封試驗裝置

往復密封多場耦合動態演化試驗裝置通過模擬實際機載工況，對往復密封件進行應力加載，對其所受的摩擦力以及泄漏量在線監測，以驗證上述所提出的模型并對往復密封的可靠性進行評估，往復密封試驗裝置的結構如圖2所示。在本研究中，摩擦力和泄漏量的數據將被采集，用來驗證所提出的模型，并對往復密封件的可靠性進行評估。

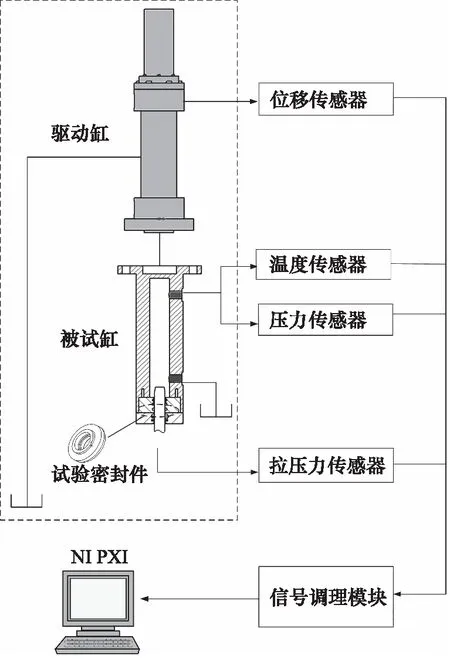
圖2 往復密封試驗裝置結構圖Fig.2 Structure diagram of reciprocating seal test device

往復密封試驗裝置的三維圖如圖3所示，試驗裝置整體采用立式結構布局。相對于臥式結構，立式結構處可以避免由活塞桿重力導致的密封件兩側受力不相等的情況，減小附加摩擦。往復密封試驗裝置的主要部件從上到下依次為驅動缸、被試缸、活塞桿和拉壓力傳感器，其中驅動缸固定在主體臺架上，其余機構通過連接板安裝于滑動導軌上，可上下移動，拉壓力傳感器用于測量往復密封件所受到的摩擦力。

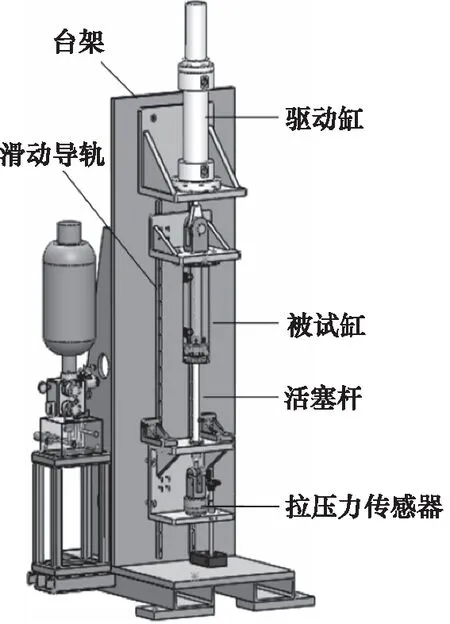
圖3 往復密封試驗裝置三維圖Fig.3 Three-dimensional diagram of reciprocating seal test rig

被試密封件安裝于被試缸下端，為了便于對密封件進行更換，設計了如圖4所示的密封件更換裝置。密封件工裝模塊內部有3個密封件安裝槽，可單個安裝不同樣式的密封件，也可進行組合密封試驗。防塵圈工裝模塊內安裝防塵圈，防止雜質進入試驗缸；側壁開孔作為泄漏油液的流出通道，用以測量往復密封的泄漏量。針對不同直徑的密封件，可采用不同內徑的密封件工裝模塊與防塵圈工裝模塊，提高往復密封試驗裝置的通用性。

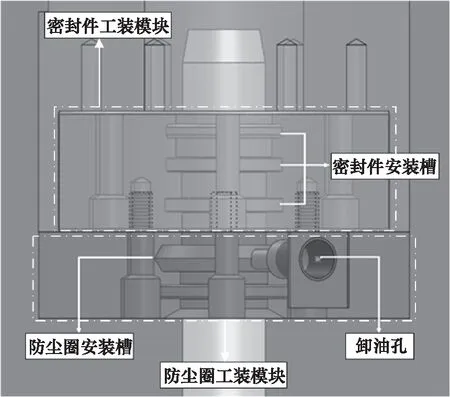
圖4 密封件更換裝置Fig.4 Seal replacement device

在被試密封件安裝好以后，調整活塞桿的位置，使得活塞桿與被試密封件之間保持同軸度且與滑動導軌平行，以避免因偏心產生的附加摩擦，最后通過螺栓將下方連接板固定臺架上。驅動缸帶動被試缸沿著滑動導軌往復運動，滑動導軌的存在，保證了往復運動過程中活塞桿與被試密封件之間的同軸度。

4.2 參數估計與可靠度評估驗證

本研究共對8個密封件進行了長達500 h的試驗，其中4組樣本的摩擦力與泄漏量退化軌跡如圖5所示。

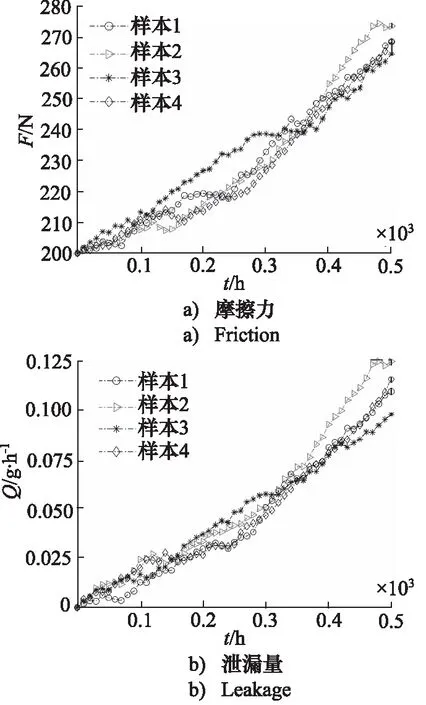
圖5 摩擦力與泄漏量退化軌跡Fig.5 Degradation of friction and leakage

根據3.1節提出的模型解算方法，可先進行第一段貝葉斯參數估計，確定密封件摩擦力和泄漏量各自的一元退化過程，即2個維納過程的參數α=(μ1,σ1,q1,μ2,σ2,q2)。由OpenBUGS軟件估算可得各參數的分布如圖6所示，其估計值在表1中列出。將維納過程參數的估計值與退化增量帶入式(3)，求得2個退化增量的分布函數，并作為二元Copula函數的輸入。

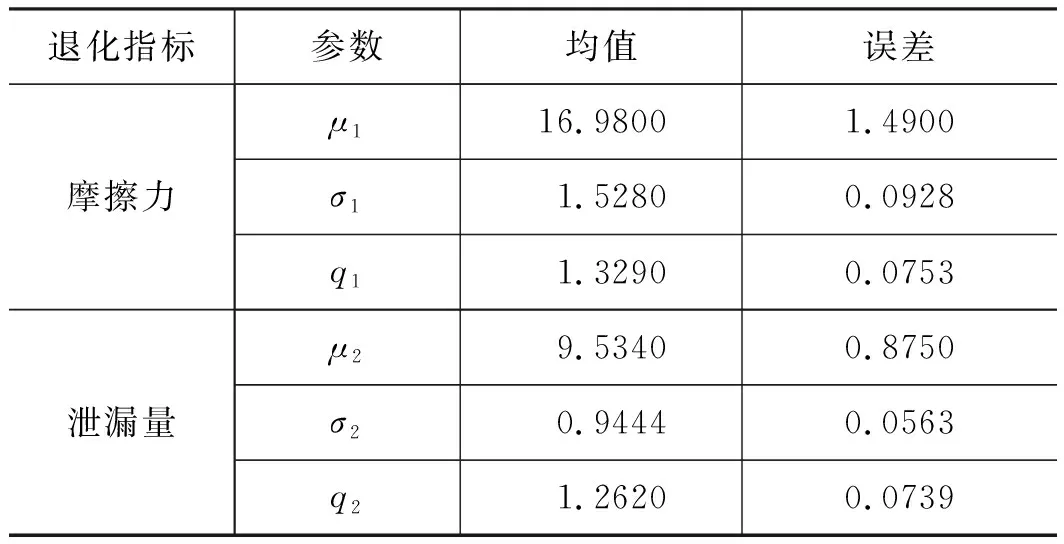
表1 維納過程各參數估計值

第二段貝葉斯參數估計，用以確定Frank Copula函數相關性系數的ARMA表達式參數，即θ=(ωθ,βθ,αθ)。由OpenBUGS軟件估算可得各參數的分布如圖7所示，其估計值在表2中列出。

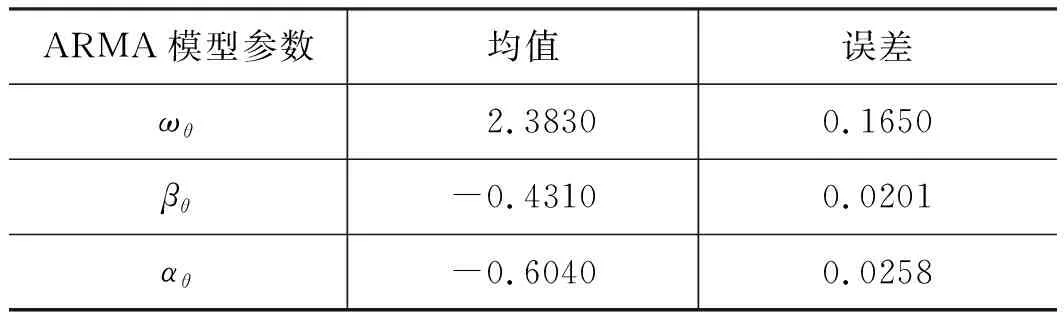
表2 ARMA模型各參數估計值Tab.2 Estimated values of parameters in ARMA model

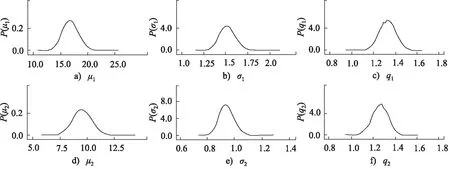
圖6 維納過程參數分布Fig.6 Distributions of parameters in Wiener process

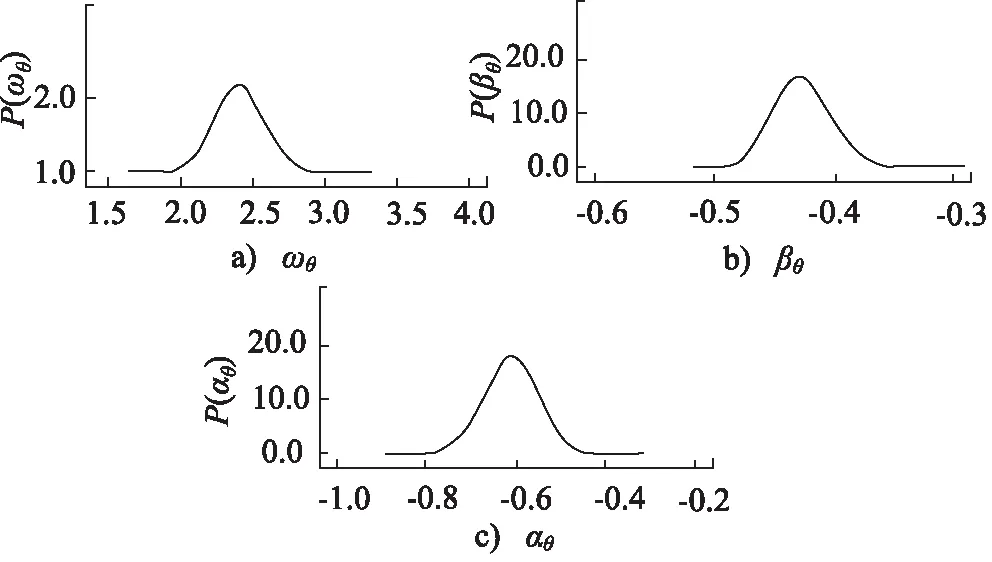
圖7 ARMA模型中各參數的分布Fig.7 Parameter distribution in ARMA model

根據表1和表2中對于模型參數的估計結果，結合式(7)和式(11)，對往復密封件的可靠性進行評估。分別對僅考慮泄漏量指標、僅考慮摩擦力指標、考慮摩擦力與泄漏量之間的相關系數為常數和摩擦力與泄漏量之間滿足ARMA時變相關這4種情況的往復密封件進行可靠性評估，結果如圖8所示。

從圖8中可以看出， 在僅考慮泄漏量或摩擦力的情況下，往復密封件的可靠度會高于綜合考慮兩者具有相關性時的可靠度，其原因是，存在某一個性能退化

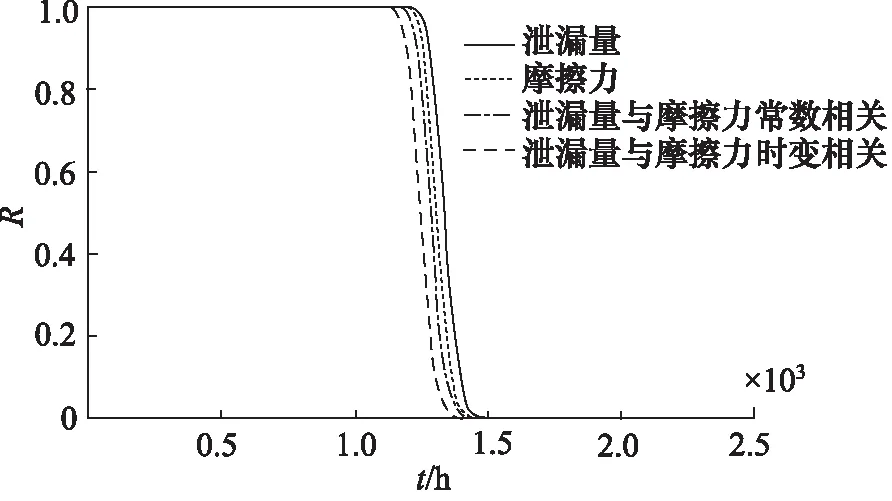
圖8 可靠度曲線Fig.8 Reliability curve

指標達到閾值時，另一性能退化指標可能早已達到失效閾值。在摩擦力和泄漏量2個性能退化指標中，摩擦力更能反映往復密封件的失效。

5 結論

提出了一種基于ARMA模型的機載往復密封二元時變相關退化模型，往復密封摩擦力和泄漏量退化軌跡用維納過程描述，采用Copula函數表示2個性能退化指標之間的相關性，并用ARMA模型表征相關性系數的時變性。采用兩段貝葉斯估計的方法對模型中的參數進行估計。最后介紹了往復密封試驗裝置，并基于此裝置的試驗數據驗證了提出的退化模型，試驗結果驗證了所提出的往復密封退化模型的準確性。