調節閥附加耦合負載的形成機制

潘子晗， 謝玉東， 韓家楨， 王 勇

(1.山東大學 機械工程學院， 山東 濟南 250061；2.山東大學 高效潔凈機械制造教育部重點實驗室， 山東 濟南 250061)

引言

艦船調節閥是指在艦船的核動力裝置的核島、常規動力裝置及其輔助控制系統的蒸汽等流體輸送中起調節作用的閥門。艦船調節閥控制著動力系統的啟動、停止和功率輸出，其結構如圖1所示。執行機構根據控制器的信號，通過閥桿帶動閥芯，改變閥芯和閥座間的通流面積，從而控制調節閥的流量或壓力。調節閥動態特性高度非線性，在一定條件下，閥內流體的動能和壓力能發生轉換，造成流量和壓力波動。在艦船實施復雜的動作時，調節閥處于啟動、關閉、調整的動態過程中，流體的振蕩與閥內構件形成非定常的流固耦合效應，振蕩的流體載荷給執行機構造成附加耦合負載。附加耦合負載與調節閥原有的負載疊加后，有可能使閥門所需的驅動力矩大于執行機構輸出的最大力矩，導致執行機構不能動作或動作異常，使調節閥失去調節能力。如果載荷繼續增大，則有可能造成閥門部件受損，進而影響艦船的航行。

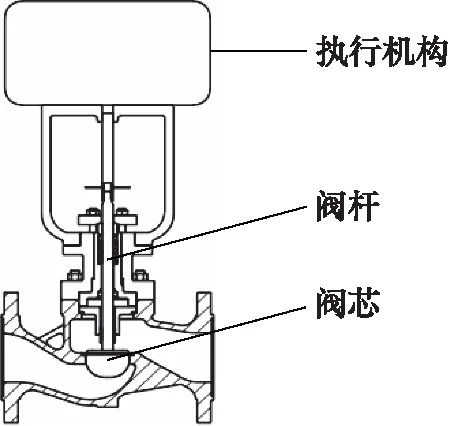
圖1 調節閥結構示意Fig.1 Diagram of control valve

近年來，一些研究者對有關調節閥流體負載開展了研究。廖瑤瑤等[1-3]采用CFD仿真模擬的方法，研究了不同閥口形態下閥芯所受液動力及動態特性。彭健等[4-7]建立了調節閥內部流場的計算模型，用流固耦合仿真分析和探討不同條件下各級壓降特性以及空化對閥門的影響。陳雨洋等[8]建立了水擊卸壓閥運動時的數學模型，在AMESim軟件中模擬實際水擊現象，分析動態特性。AHUJA V等[9-10]對閥門進行了非定常流動仿真并計算動態負載。HAN等[11]用AMESim-Fluent聯合仿真模擬調節閥運動，對其流體振蕩進行數值分析。湯志勇等[12-13]推導得出了錐閥動態液動力的計算公式，研究了液動力在低頻和高頻下的頻率響應，并進行實驗驗證。SORENSEN等[14]對不同閥座液壓閥的液動力進行了數值分析。鄭淑娟等[15]對運動狀態的液壓錐閥流場作了仿真分析。

目前，對于艦船用調節閥等非液壓系統調節閥以及其附加耦合負載的國內外相關研究較少。為了使艦船在執行任務時其動力系統不會因調節閥而發生故障，本研究通過對調節閥的有限元建模，設置調節閥閥芯移動方向、不同的突變壓力值及閥芯運動速度，分析每組仿真的閥芯軸向受力及壓力情況，討論調節閥在不同外界突變壓力、不同閥芯調節速度下的附加耦合負載狀況；以探究調節閥在動態調節中附加耦合負載規律，為動態負載的補償提供基礎規律，并為艦船調節閥的安全穩定運行提供參考。

1 仿真方法

1.1 仿真模型的建立及網格劃分

本研究選用一種線性流量特性的調節閥建立仿真流道模型，其閥腔及周圍縱剖示意如圖2所示，其具體參數見表1。本研究建立了2個調節閥流道模型進行流體仿真，閥芯分別處于起始開度40%與起始開度100%的2個位置，模擬艦船調節閥在不同行程下控制流體的過程。起始開度40%，閥芯從下向上移動，開度增大，以研究在調節閥調節至50%左右調節閥內部的負載變化；閥芯的起始開度100%，閥芯從上向下移動，開度減小，以研究閥門在大開度向下調節時調節閥內部的負載變化，網格模型如圖3～圖4所示。

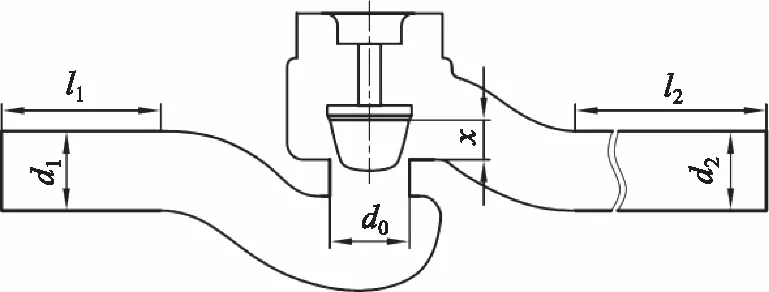
圖2 調節閥流道模型部分縱剖示意

圖3 調節閥流道網格模型Fig.3 Grid model of flow passage in control valve

圖4 調節閥閥芯周圍縱剖網格模型Fig.4 Longitudinal grid model around control valve spool

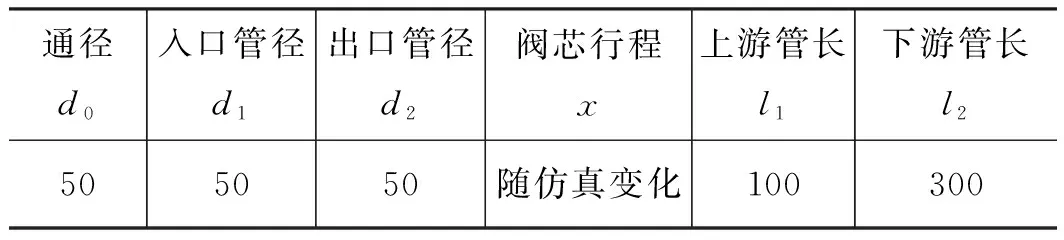
表1 調節閥模型參數Tab.1 Parameters of control valve model mm

1.2 仿真參數的設置

為了分析流體和閥芯運動等不同條件的變化對閥門所受負載的影響，仿真設定閥芯運動速度變化和突變壓力變化兩類工況，分別進行具體的自定義函數設置。

仿真通過使管路內的壓力突變來模擬艦船在運行時戰術動作的突然轉換，主要設置網格模型中入口壓力這一邊界條件的變化規律。本研究設置的壓力變化規律如圖5所示，壓力最大值pmax取5，13，17，21 MPa 4種情況，在仿真開始0.06 s后施加突變壓力并瞬間達到最大值pmax，持續0.04 s后瞬間恢復至原來的壓力。

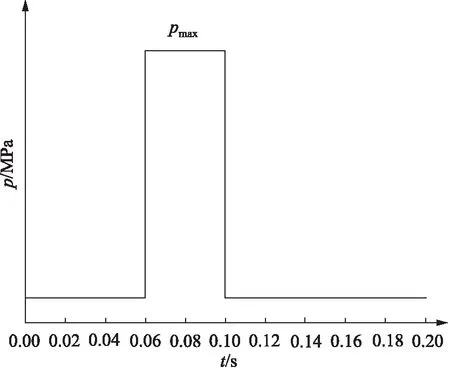
圖5 調節閥仿真壓力變化規律Fig.5 Pressure change in control valve

閥芯運動速度變化工況通過控制網格模型中的閥芯部分沿軸線方向進行直線運動，以模擬閥門在不同的指令速度要求下的調節過程。起始開度40%的網格模型，設置閥芯分別以40， 60， 80， 100 mm/s的速度向上移動；起始開度100%的模型，設置閥芯以同樣大小的4組速度向下移動；相對位移8 mm，在相對位移xr=3 mm處施加艦船管路突變壓力，xr=4.8 mm處撤去壓力。

仿真需分析閥門的附加耦合負載，包括閥芯的軸向受力、閥芯穩態壓力和閥芯動態壓力。其中閥芯軸向受力直觀地體現閥芯的軸向負載變化情況，而穩態壓力和動態壓力則參與計算閥芯的液動力，其計算公式如式(1)所示：

Ff=Fs-Fd

(1)

式中，Ff—— 液動力

Fs—— 穩態壓力引起的負載

Fd—— 動態壓力引起的負載

其中,Fs和Fd的計算方法如式(2)、式(3)[16]所示：

(2)

(3)

式中，ps—— 穩態壓力

pd—— 動態壓力

Sc—— 閥芯在軸向的投影面積

在Fluent中，閥芯的穩態壓力表示閥芯表面的流體靜壓，反映流體的壓力能對閥芯的影響；而動態壓力表示閥芯表面流體的動壓，反映流體的動能對閥芯的影響，在仿真中，二者的大小均隨著模擬艦船工況的改變而不斷變化。由于選用調節閥的閥芯表面不是錐面，較難直接計算整個閥芯受的液動力。因此，選擇直接對比分析其穩態與動態壓力，間接分析閥芯受到的液動力的變化，從而推斷附加耦合負載。

2 仿真結果與討論

2.1 艦船壓力突變工況

固定閥芯的移動速度，改變最大突變壓力，模擬不同劇烈程度下的艦船管路壓力突變，分別得到起始開度40%與100%的仿真結果。

1) 起始開度40%

閥芯從起始位置以40 mm/s的速度向上運動，在第0.06秒時施加突變壓力，第0.1秒時撤去壓力，分別導出仿真的軸向力Fa、穩態壓力ps和動態壓力pd，如圖6～圖8所示。

圖6 不同突變壓力下閥芯軸向力變化(起始開度40%)Fig.6 Axial force change of spool with different mutation pressures (initial opening 40%)

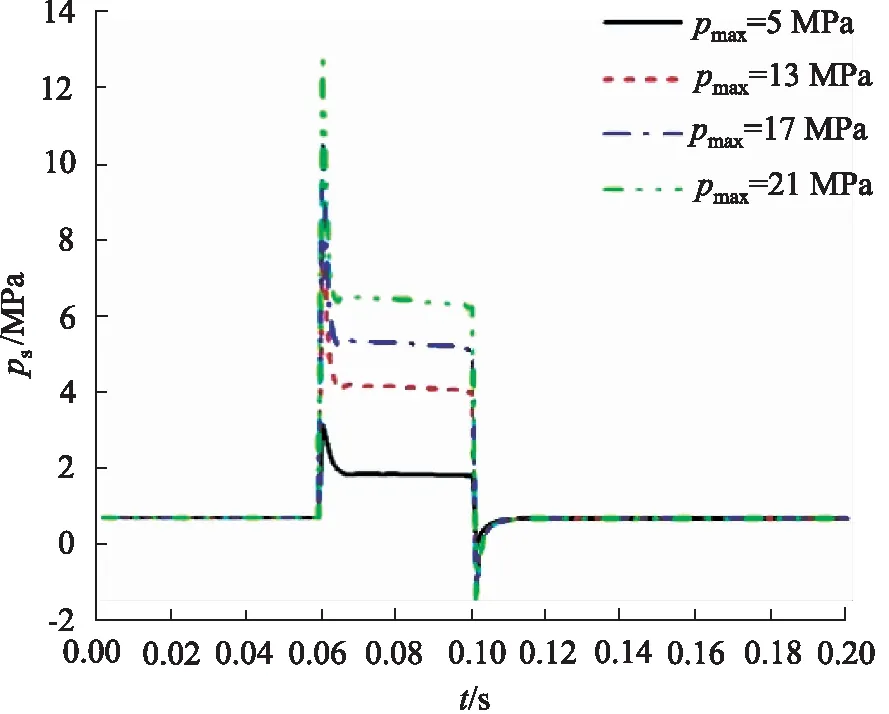
圖7 不同突變壓力下閥芯穩態壓力變化(起始開度40%)Fig.7 Static pressure change of spool with different mutation pressures (initial opening 40%)

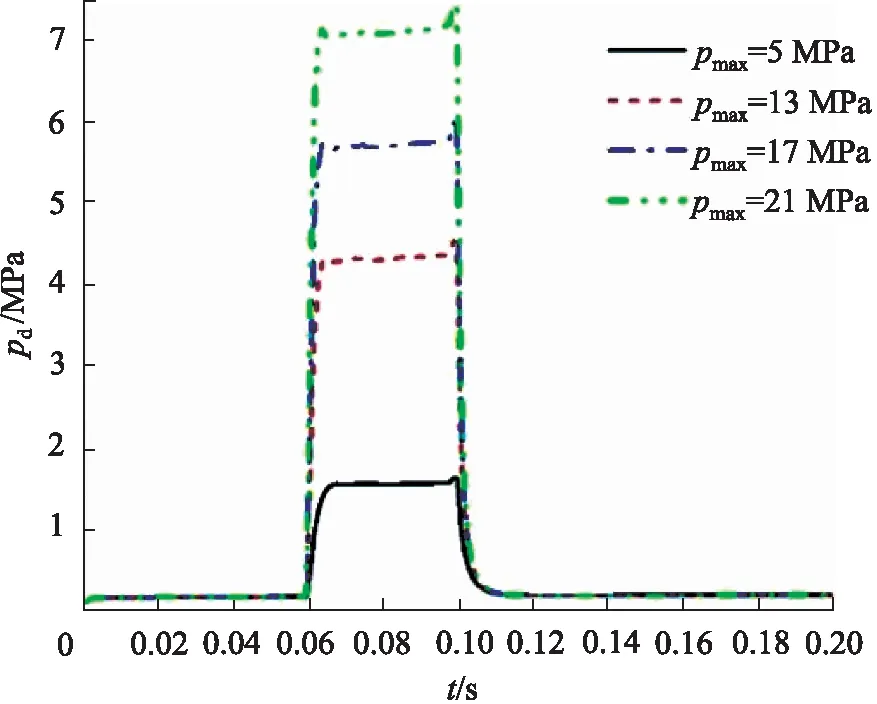
圖8 不同突變壓力下閥芯動態壓力變化(起始開度40%)Fig.8 Dynamic pressure change of spool with different mutation pressures (initial opening 40%)

由圖6可知，pmax為5 MPa時的曲線沒有明顯的尖峰和波動，其他3種情況下的曲線作放大處理可以看出，突變壓力施加后，調節閥的閥芯受力在0.005 s內迅速上升并出現峰值，最大受力接近22 kN，上升時間隨pmax的增大而減小；在突變壓力即將撤去前， 閥芯受力上升約0.2 kN。由圖7得，在突變壓力施加時，穩態壓力最大值約為pmax的60%，經過最大值后，pmax越大，穩態壓力下降斜率越大；突變壓力撤去時，出現了負壓， 在0.02 s內恢復到正常壓力值。 圖8可知， 閥芯所受的動態壓力最大值出現在突變壓力即將撤去前，仿真過程的最大動態壓力接近7.5 MPa。結合圖7與圖8分析，突變壓力施加的時間段之外，閥芯的穩態壓力大于0.5 MPa，而動態壓力小于0.5 MPa，說明在這段時間內穩態壓力對閥芯附加耦合負載的影響較大；pmax為5 MPa時，穩、動態壓力差約為0.1 MPa，pmax為21 MPa時，穩、動態壓力差約為-0.7 MPa，說明隨著閥門內部突變壓力的升高，動態壓力對閥芯負載的影響逐漸起到主導作用。

閥芯周圍的流場壓力及速度云圖，如圖9、圖10所示。由圖9a可得，在突變壓力(pmax=13 MPa)施加時，閥芯下部壓力接近13 MPa，閥芯上部壓力約為2 MPa，且在閥芯的上部邊緣處出現負壓區。由圖10a得，pmax為21 MPa時閥芯周圍負壓區的面積擴大。對比圖9b和圖10b，pmax為13 MPa的突變壓力施加時，最大流速達到140 m/s，pmax為21 MPa時，最大流速達到170 m/s；當突變壓力撤去后，二者閥芯周圍最大速度為約58 m/s；閥芯左側存在有2個旋渦，閥芯左下方有1個較小的旋渦，緊貼在側壁上，在突變壓力撤去時，pmax為13 MPa時閥芯右上方有旋渦出現，而pmax為21 MPa時對應位置無旋渦生成。

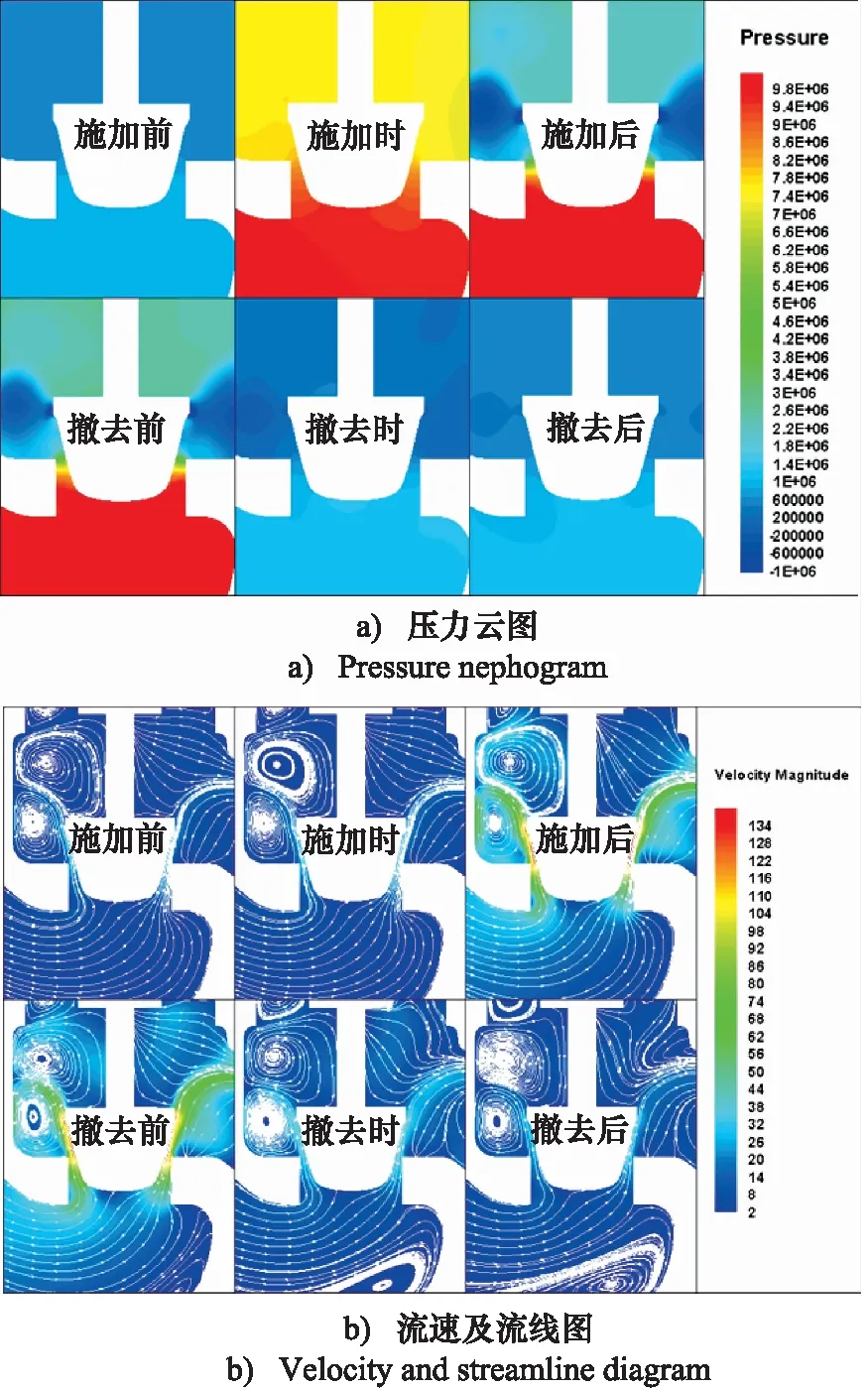
圖9 閥芯周圍流場情況(pmax=13 MPa，起始開度100%)Fig.9 Flow field around spool (pmax =13 MPa, initial opening 40%)

圖10 閥芯周圍流場情況(pmax=21 MPa，起始開度100%)Fig.10 Flow field around spool (pmax =21 MPa， initial opening 40%)

2) 起始開度100%

起始開度100%時調節閥模型的軸向力與壓力隨時間的變化規律，如圖11～圖13所示。

由圖11得，當突變壓力為21 MPa時軸向力最大，為11 kN。在壓力突變段內，4條曲線的壓力增加率均高于其他時間段。圖11b局部放大圖得，在壓力突變時，當pmax分別為13，17， 21 MPa時的3條曲線在經過0.003 s后達到一個峰值，隨后呈波動上升趨勢。如圖12所示，閥芯所受穩態壓力在入口壓力發生突變時出現明顯的尖峰， 后迅速下降，達到相對穩定的壓力，每條曲線的穩定壓力值接近pmax的30%，而峰值大小約為pmax的60%。當入口壓力突然減小到正常壓力值時，閥芯出現了負壓。圖13顯示閥芯所受動態壓力最大值出現在pmax為21 MPa條件下，約為8.8 MPa。峰值之后穩定在最大突變壓力的40%左右。結合圖12與圖13，在突變壓力施加時，穩態動態壓力差隨pmax的增加而增大，pmax為21 MPa時，達到-2.5 MPa左右。

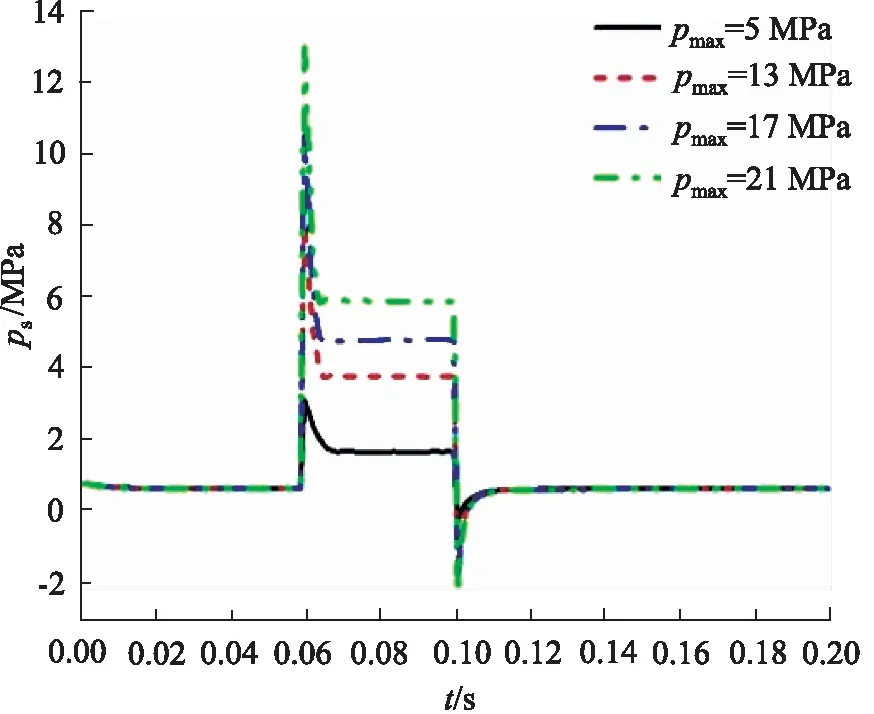
圖12 不同突變壓力下閥芯穩態壓力變化(起始開度100%)Fig.12 Static pressure change of spool with different mutation pressures (initial opening 100%)

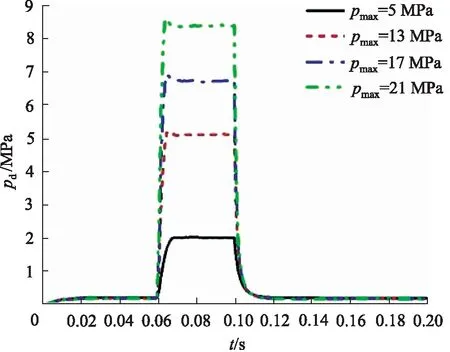
圖13 不同突變壓力下閥芯動態壓力變化(起始開度100%)Fig.13 Dynamic pressure change of spool with different mutation pressures (initial opening 100%)

起始開度100%，pmax分別為13，21 MPa時閥芯周圍流速及流線圖，如圖14、圖15所示。pmax為13 MPa時，最大流速達到140 m/s；pmax為21 MPa的突變壓力施加時，最大流速達到178 m/s。從流線觀察，pmax為13 MPa時，突變壓力施加后瞬間，其在閥芯右上方出現了1個較小的旋渦；pmax為21 MPa時，在此位置沒有明顯的旋渦生成。而在突變壓力撤去時，兩圖的閥芯右上方的出現旋渦，當流場相對穩定后，此旋渦移動至閥腔邊緣，閥芯右下方流道內部的旋渦也隨之出現。

圖14 閥芯周圍流速及流線圖(pmax=13 MPa，起始開度100%)Fig.14 Velocity and streamline around spool (pmax=13 MPa, initial opening 100%)

圖15 閥芯周圍流速及流線圖(pmax=21 MPa，起始開度100%)Fig.15 Velocity and streamline around spool (pmax=21 MPa, initial opening 100%)

2.2 閥芯速度變化工況

固定艦船的管路突變壓力，改變艦船調節閥閥芯移動速度，分別得到起始開度40%與100%的仿真結果。

1) 起始開度40%

閥芯從起始位置分別以40，60，80，100 mm/s的速度向上運動，在相對位移xr為3 mm處施加艦船管路13 MPa突變壓力，xr為4.8 mm處撤去壓力，得到閥芯軸向受力、穩態壓力和動態壓力，如圖16～圖18所示。

由圖16a可得，閥芯所受軸向力在突變壓力施加的時間段內呈現波動下降；最大軸向力約12.18 kN，此時閥芯速度40 mm/s，軸向力的峰值隨閥芯速度的增加而減小，各移動速度下的閥芯受力均呈現較為明顯的波動。其中閥芯速度60 mm/s時受力在峰值之后是最小的。如圖16b所示， 峰值時間最短為閥芯速度100 mm/s時，約為0.0047 s。閥芯移動速度增加，其軸向力波動的頻率逐漸增加。

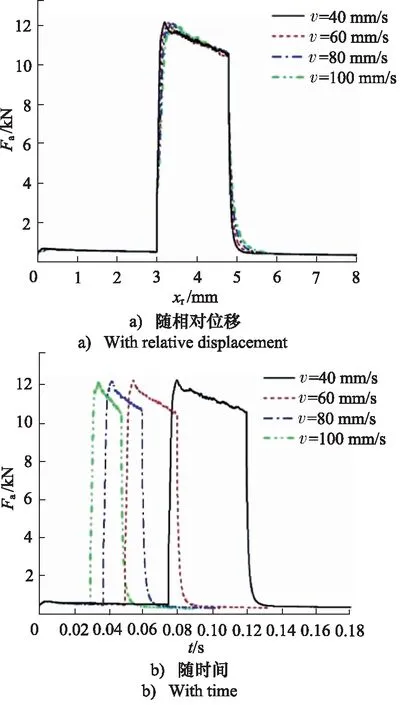
圖16 不同閥芯速度下閥芯軸向力變化曲線(起始開度40%)Fig.16 Axial force change of spool with different speeds (initial opening 40%)

由圖17得，經過峰值后，閥芯的穩態壓力沿斜率較小的直線下降，4條曲線在此段幾乎重合。圖18可知，閥芯所受的動態壓力在突變壓力施加時迅速上升并出現波動，最大值出現在閥芯速度為40 mm/s時，約為4.8 MPa。結合圖17與圖18，在突變壓力施加時，靜、動態壓力差達到-0.6 MPa。圖16～圖18說明，隨著突變壓力施加，閥芯受到的附加耦合負載隨著閥芯的移動而不斷波動，閥芯的運動速度越大，附加耦合負載的波動頻率越大，閥芯受力就越不穩定。

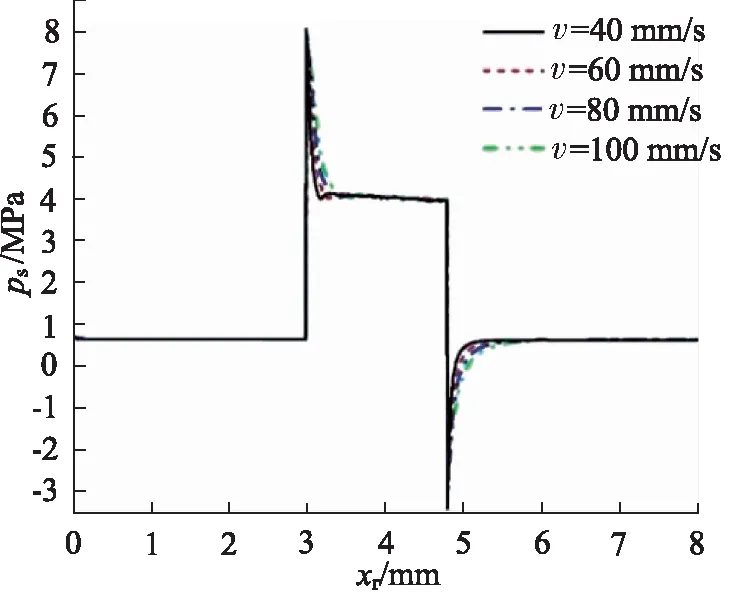
圖17 不同閥芯速度下閥芯穩態壓力變化(起始開度40%)Fig.17 Static pressure change of spool with different speeds (initial opening 40%)

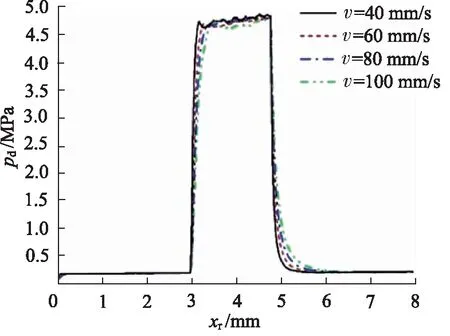
圖18 不同閥芯速度下閥芯動態壓力變化(起始開度40%)Fig.18 Dynamic pressure change of spool with different speeds (initial opening 40%)

2) 起始開度100%

閥芯從起始位置分別以v為40，60，80，100 mm/s的速度向下運動。

從圖19a可得，閥芯所受軸向力在突變壓力施加的時間段內呈現波動上升；突變壓力施加時，調節閥的閥芯受力出現峰值，約5480 N，此時閥芯速度100 mm/s；仿真過程的最大值出現在速度60 mm/s突變壓力即將撤去時，為6900 N。閥芯受力的峰值時間如圖19b所示，每條曲線的峰值時間均接近0.005 s。

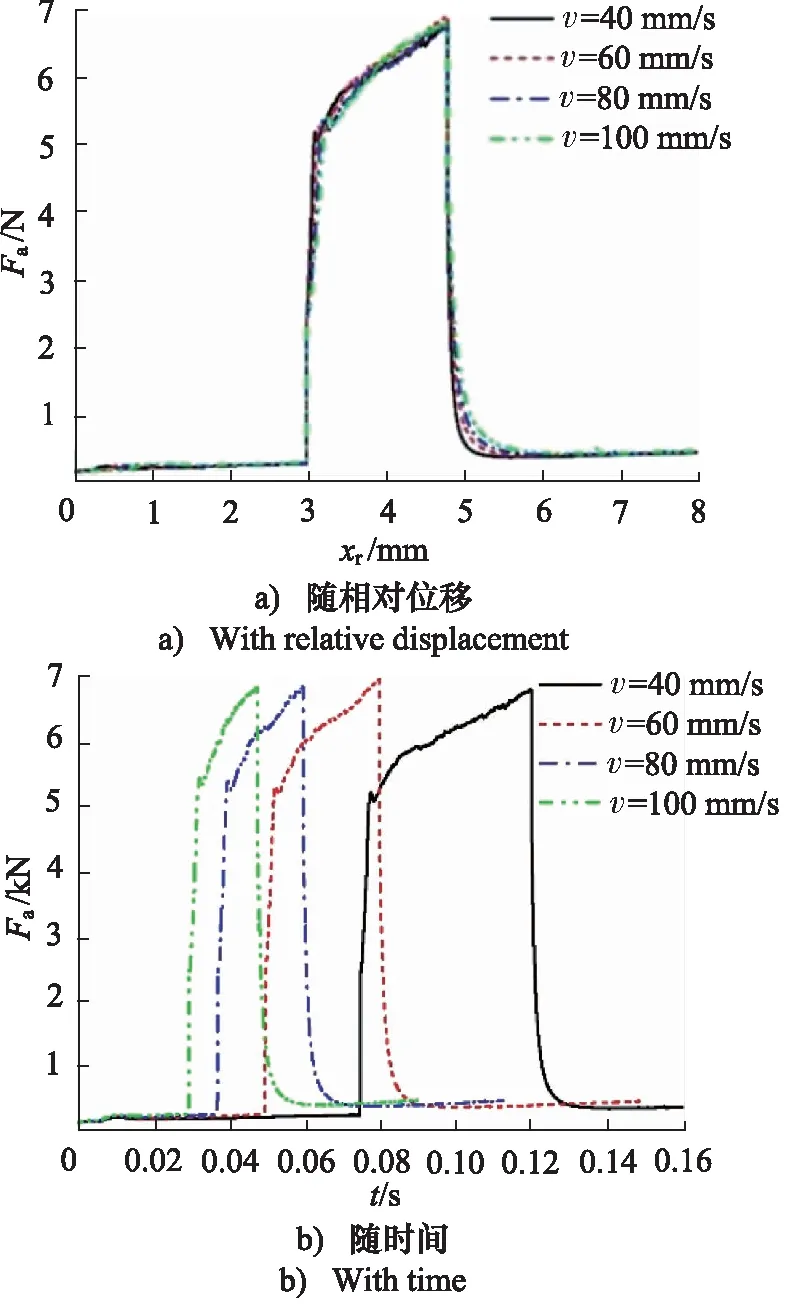
圖19 不同閥芯速度下閥芯軸向力變化(起始開度100%) Fig.19 Axial force change of spool with different speeds (initial opening 100%)

由圖20得，在突變壓力施加時，閥芯所受穩態壓力出現明顯的尖峰，約為pmax的60%。經過峰值后，穩態壓力穩定在3.8 MPa左右。突變壓力撤去時出現了負壓，約為-3.4 MPa。由圖21可知，閥芯所受的動態壓力最大值出現在閥芯速度80 mm/s時，約為5.3 MPa。結合圖20與圖21，突變壓力施加時，靜、動態壓力差達到-1.6 MPa左右，說明閥芯運動速度的大小對壓力差的影響很小。

圖20 不同閥芯速度下閥芯穩態壓力變化(起始開度100%)Fig.20 Static pressure change of spool with different speeds (initial opening 100%)

圖21 不同閥芯速度下閥芯動態壓力變化(起始開度100%)Fig.21 Dynamic pressure change of spool with different speeds (initial opening 100%)

3 結論

(1) 艦船管路內的壓力和調節閥閥芯的移動速度產生較大改變時， 調節閥受到的附加耦合負載也會產生相應變化。閥芯從下向上移動調節時，其附加耦合負載逐漸減小；閥芯從上向下移動，附加耦合負載逐漸增大。流體輸入調節閥的壓力變化對附加耦合負載的影響較大，而閥芯本身在調節過程中，因為閥芯的移動而受到的附加耦合負載變化較小；

(2) 隨著艦船管路壓力的增大，閥芯受到動態壓力逐漸超過穩態壓力，附加耦合負載隨著動態壓力而不斷波動。同時閥芯的運動速度越大，軸向受力波動頻率越大。閥芯仿真過程中，閥芯受到的最大軸向受力已經超過20 kN，受到的最大穩態壓力接近13 MPa，若此受力超過執行機構的最大輸出力，調節閥將失去調節能力，影響艦船航行安全；

(3) 附加耦合負載會使閥門內部產生負壓，閥腔內部的流體在閥芯周圍出現空化現象，隨著附加耦合負載的增大，負壓區增大。不僅會影響調節閥的調節，而且會造成閥芯損傷，縮短調節閥相關零部件的使用壽命。在這種情況下，以上結果可對艦船調節閥的控制及設計進行參考，下一步可對附加耦合負載的補償方法進行探討。