有限時間不確定性估計的電液伺服跟蹤控制技術
李 帥, 郭 慶, 蔣 丹
(1.電子科技大學 航空航天學院, 四川 成都 611731; 2.電子科技大學 機械與電氣工程學院, 四川 成都 611731)
引言
作為一類典型的機電系統,電液伺服系統憑借其超大的能量密度以及超高的調節精度,被廣泛應用于工業工程應用中,如風力機、機器人以及熱壓成型機等[1-3]。作為電液伺服系統研究的一個重要方向,控制算法的研究一直以來都備受學者們的關注, 多種控制器的設計方法都被應用到了電液伺服系統中,比如滑模控制器[4]、神經網絡控制器[5]和魯棒積分控制器[6]等。但這幾類控制器都有著十分明顯的優缺點:滑模控制器的構造方式更為簡單并且相應性能更加出色, 但在控制過程中極易出現振顫現象,進而影響控制效果;神經網絡控制器具備很好的魯棒性以及學習能力,但容易陷入局部最優解中;魯棒積分控制器在穩態區間內具有極佳的控制性能,但在瞬態區間內的控制效果欠佳。本研究采用了反步控制方法來對電液伺服系統進行控制器設計。相較于之前列舉的幾類控制器,反步控制器的魯棒性優秀,全局求解能力卓越并且在瞬態和穩態都有不錯的控制能力。雖然反步控制器的設計步驟較為復雜,但鑒于可參考的成果較多[7-9],可為本研究的研究提供足夠的幫助。
除了控制器的設計之外,由于參數不確定性的存在,如何對電液伺服系統的這類擾動進行補償就成為十分迫切的問題。事實上,很多種觀測器已經應用于電液伺服系統的控制當中,比如自適應觀測器[10-11]、高增益觀測器[12]以及擴展狀態觀測器[13]等。自適應觀測器憑借其較簡單的結構,廣泛應用于對系統全狀態的估計當中。高增益觀測器具有更好的控制精度,但同時所需的控制帶寬也更大;擴展狀態觀測器可以在模型信息未知的前提下對系統的狀態和模型進行估計。通過以上介紹可知,參數不確定性的估計精度已經得到極大的提高,但另一方面,參數不確定性估計速度一直沒有被重視,是一個可以研究的發展方向。
作為一種可以對參數不確定性進行快速估計的觀測器,終端滑模觀測器自2009年問世以來便得到了大量學者們的關注,并廣泛應用于各類機電系統中,比如永磁同步電機[14]、Buck變換器[15]、風力機組[16]等,這類觀測器對不確定性的估計速度更快,進而使得被研究系統的輸出響應效果更好。事實上在現階段的電液伺服系統控制研究中,各類觀測器對系統參數不確定性的估計精度已經達到了十分理想的水平,基于此,如何更加快速地估計參數不確定性成為了一個十分有意義的研究方向。
本研究的主要貢獻是將反步控制器的控制方法同終端滑模觀測器的設計相結合,得到了一種新的電液伺服控制系統的控制算法,通過工程平臺的實驗驗證,結果表明,新的控制算法確實能夠得到更好的控制效果,使得電液伺服系統的輸出響應結果更加出色。
1 電液伺服系統數學建模
電液伺服系統一般包括泵站、伺服閥、液壓缸以及負載對象,如圖1所示[17-18]。
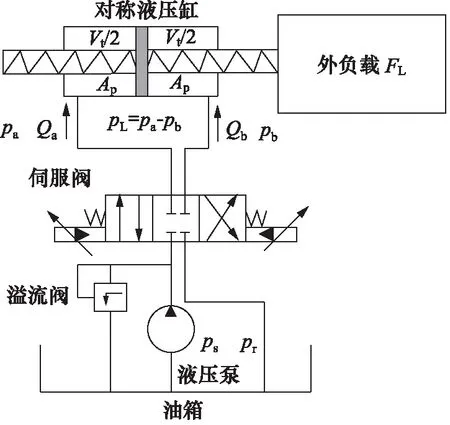
圖1 電液伺服系統示意圖Fig.1 Diagram of electrohydraulic servo systems
(1)
式中,
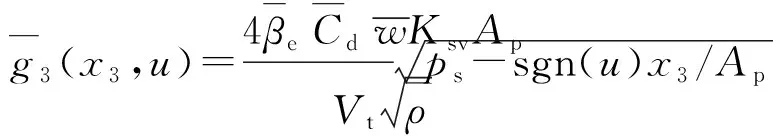
(2)
sgn函數定義為:
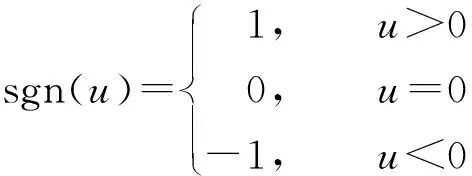
(3)
假設1:兩個集總不確定性Δ2和Δ3是有界的,滿足|Δi|≤Di,i∈{2,3},其中Di為已知的正常數。
2 終端滑模觀測器設計
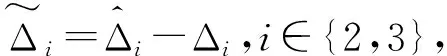
定義終端滑模面為:
(4)
其中,輔助變量v2和v3被定義為:
(5)
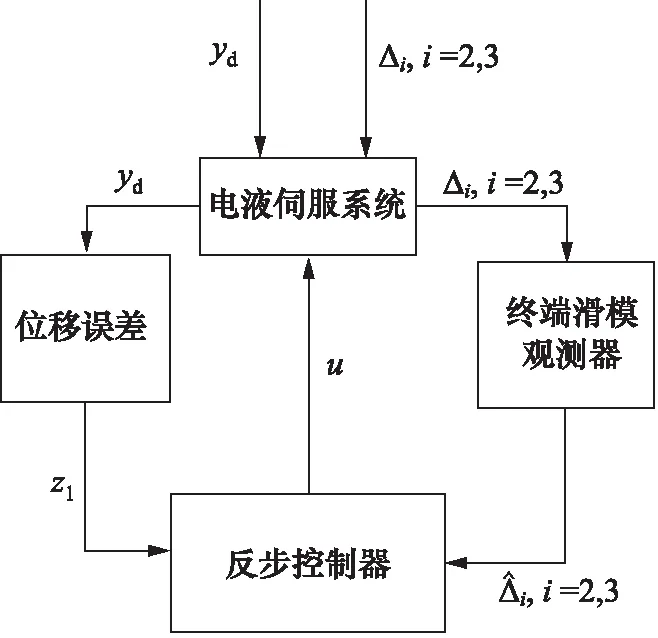
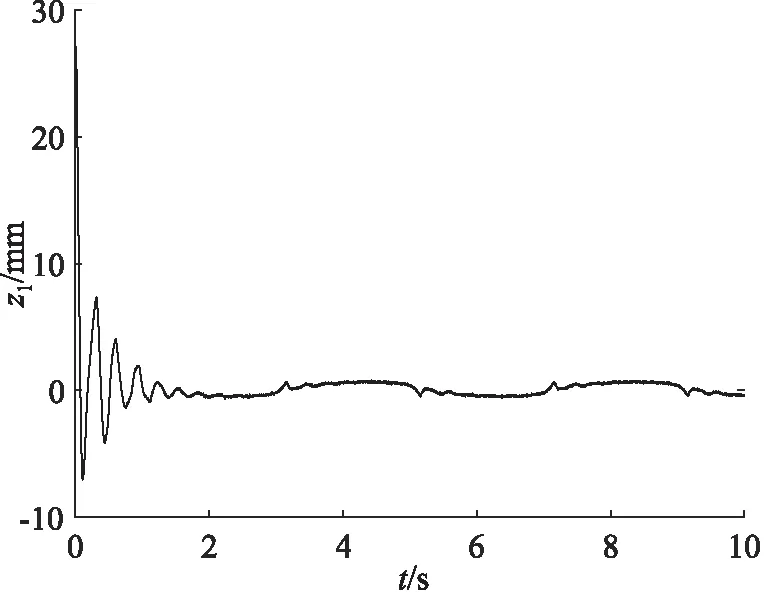
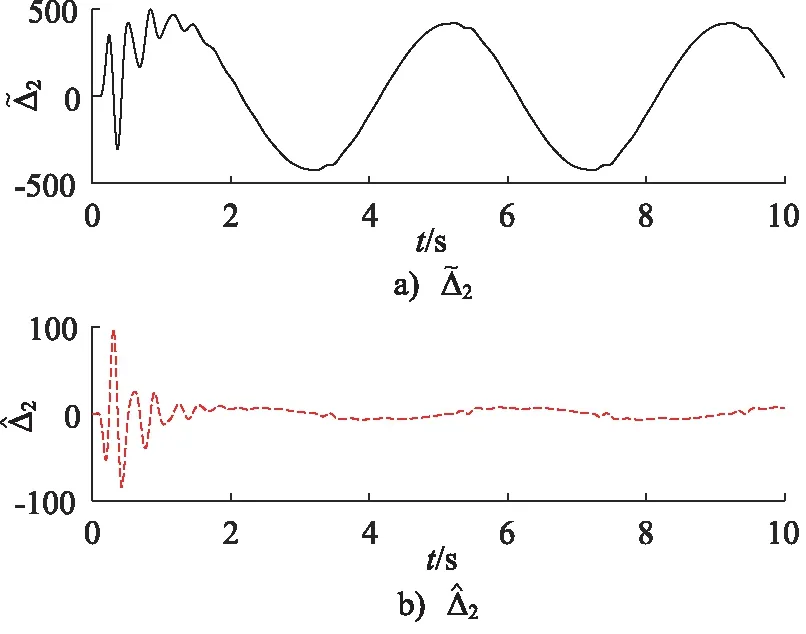
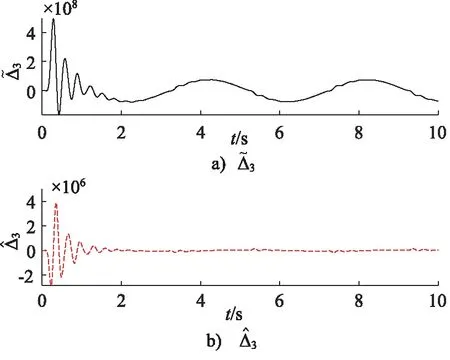
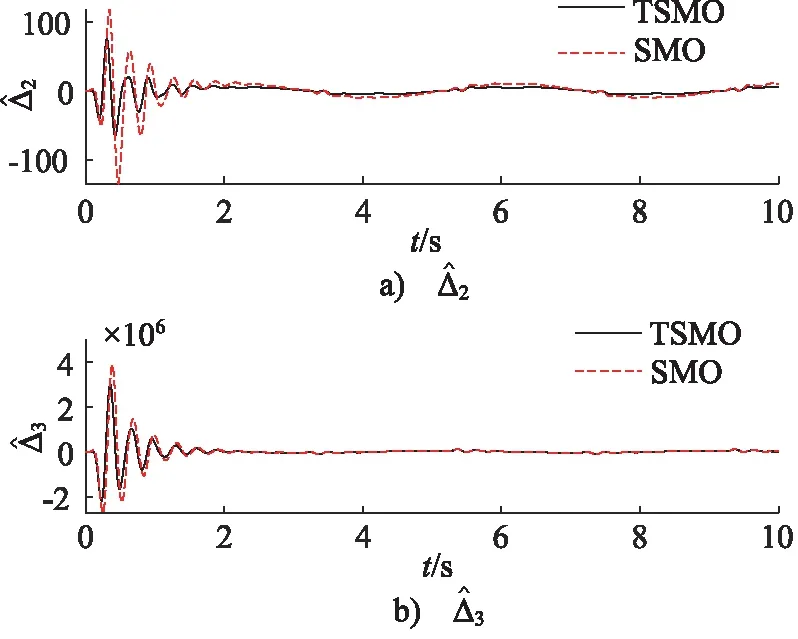
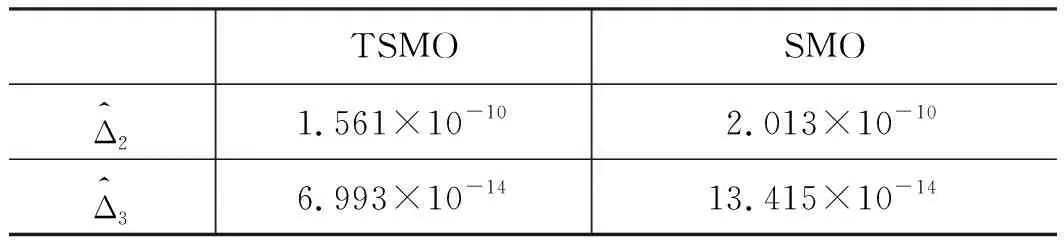
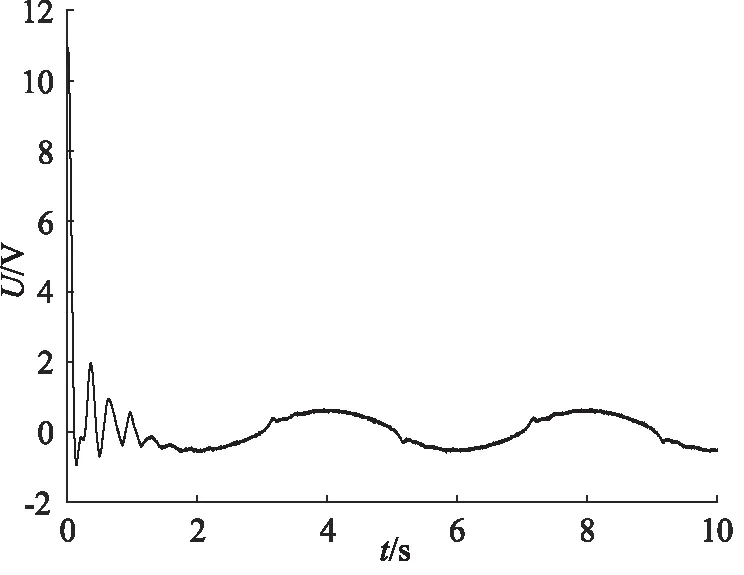
式中,kdi,di和εi為正常數,pi和qi均為正奇數,且pi 那么終端滑模觀測器估計值表示為: (6) 引理1[19]:如果存在一個正定的李亞普夫函數V(t) 滿足: (7) 式中,a,b>0,0 (8) 證明:針對集總式不確定項Δ2,選擇李雅普諾夫函數如下: (9) 則Vs2的導數為: |s2||Δ2| (10) 基于假設1,進而得出: (11) 而估計誤差為: (12) 同理,針對集總式不確定項Δ3,選擇李雅普諾夫函數如下: (13) 則Vs3的導數為: |s3||Δ3| (14) 又基于假設1,可進而得出: (15) 而估計誤差為: (16) 此部分將會提出一個基于終端滑模觀測器的反步控制器的設計算法,首先,給定一組誤差方程如下: (17) 并將此誤差方程進行求導,得出: (18) 為了實現電液伺服系統的位移跟蹤控制,2個虛擬控制變量α1,α2以及1個控制輸入u將被定義為: (19) 式中,k1,k2和k3是3個可調節的控制增益,均是大于0的常數。 定理2:對于電液伺服系統式(1),若考慮終端滑模觀測器式(4)~式(6)以及遞歸反步控制器式(17),那么,此系統將會漸進跟蹤期望軌跡yd,從而實現了所需的控制效果。 證明:首先,構造李雅普諾夫函數如下: (20) 并根據此李雅普諾夫函數構造一系列的級聯項如下: (21) 由于控制器是基于反步法進行設計的,所以本研究將會把接下來的穩定性證明分為3個步驟進行分析。 第一步:結合式(17)~式(19),可以得出: (22) 第二步:根據式(12)、式(17)~式(19)、式(22),可以得出: (23) 第三步:根據式(16)、式(19)、式(23),可以得出: ≤0 (24) 由于V3=V,所以不等式(24)也說明狀態變量x1,x2,x3將會漸進地收斂到平衡點,這也說明了本研究所設計的控制器實現了電液伺服系統的漸進追蹤控制。 證明完畢。 本研究所提出的控制策略的流程圖如圖2所示。 圖2 控制流程圖Fig.2 Control flow diagram 為了驗證本研究所提出的控制策略,搭建了一個實驗平臺,組成部分如下:泵站(HY-36CC-01/11 kW),噴嘴擋板伺服閥(D633-R04K01M0NSM2),液壓缸(UG1511R25/16-100),如圖3所示。 圖3 電液伺服系統實驗平臺Fig.3 Experimental platform of electro-hydraulic servo systems 在實驗過程中,液壓缸的位移數據通過位移轉換器(BD-sensors-DMP-331)進行傳輸,并且同液壓缸負載壓力一起被NI卡(PCI-6237/21 DA1)進行采集。基于采集的數據,本研究所提出的控制算法便可以由上位機的MATLAB軟件進行構造,并通過NI卡傳遞至伺服閥,進而實現控制目的。由于考慮了氣缸位置的機械約束和伺服閥的控制飽和,本研究設定期望軌跡是一個頻率和幅度都不高的正弦曲線。 由于所提出的控制算法是針對單個電液伺服系統的控制算法,所以圖3中只有一個執行器被控制。為了說明結論的可行性,本研究設計終端滑模觀測器參數kd2=66,kd3=1.5,D2=2,D3=2,ε2=88,ε3=3,以及分數項p2/q2=p3/q3=5/7,并給定控制器參數k1=370,k2=300,k3=600。基于以上參數,電液伺服系統實驗平臺可實現追蹤控制。 圖4展示了實驗當中的實際位移y與期望軌跡yd。經過前期的一段振顫后,實際位移y逐漸趨近于期望軌跡yd。兩條軌跡的誤差如圖5所示,經過前期的一段振顫后,實際位移y與期望軌跡yd的位移誤差收斂于0。 圖4 實驗中的實際位移與期望位移Fig.4 Actual and expected positions in experiment 圖5 實際位移與期望位移間的位移誤差Fig.5 Position error between actual and expected position 圖6和圖7分別為參數不確定性項Δ2和Δ3的估計值與估計誤差,經過前期的一段振顫后,估計誤差逐漸收斂到0。圖8為終端滑模觀測器(TSMO)與常規滑模觀測器(SMO)的估計誤差數據。終端滑模觀測器的估計誤差在前期振顫階段相較于常規滑模觀測器具備更小的振幅,體現出了終端滑模觀測器的優越性。表1對2種觀測器的估計誤差進行了量化,對比表中數據,依然可得出終端滑模觀測器具備更好的擾動估計性能的結論。 圖6 Δ2的估計值及估計誤差Fig.6 Estimation value and estimation error of Δ2 圖7 Δ3的估計值及估計誤差Fig.7 Estimation value and estimation error of Δ3 圖8 終端滑模觀測器與滑模觀測器對比Fig.8 Contrast between TSMO and SMO 表1 終端滑模觀測器與滑模觀測器的估計誤差Tab.1 Estimation errors of TSMO and SMO 圖9為實驗中的控制輸入電壓,由于本研究給定的期望軌跡是正弦信號,所以控制輸入也近似于正弦波。 圖9 實驗中的控制輸入Fig.9 Control input in experiment 本研究提出了一種全新的電液伺服控制算法。首先,為電液伺服系統設計了終端滑模觀測器,對電液伺服系統所存在的參數不確定性進行估計和補償;在此基礎上,本研究設計并提出了反步控制算法,來實現電液伺服系統的跟蹤控制;最后,通過平臺實驗,驗證了算法的可行性。通過以上的研究發現,終端滑模觀測器相較于常規的滑模觀測器,可以對電液伺服系統的參數不確定性進行更為快速地估計,進而提升電液伺服系統的跟蹤控制性能。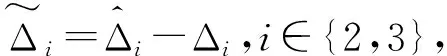
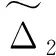
3 反步控制器設計
4 實驗驗證


5 結論

