邊緣計算中多設備多任務的能耗均衡優化算法

龐 源，武繼剛，陳 龍，姚棉陽

廣東工業大學 計算機學院，廣州510006

近年來，隨著科學技術水平的提高，增強現實、虛擬現實、實時游戲等時延敏感型應用迅速發展。此類應用的發展通常需要高性能機器支持。然而，隨著移動設備的普及，用戶傾向于在移動設備上完成各項任務。當用戶希望在移動設備上完成各項任務，包括時延敏感型應用，就需要移動設備擁有足夠強大的計算能力和續航能力。但是，由于移動設備的便攜性，其體積通常不會很大，其計算能力和續航能力無法得到保證。為此，歐洲電信標準協會引入了移動邊緣計算（mobile edge computing，MEC）來解決這個問題。近幾年來，MEC 發展迅速，在視頻內容傳輸、無人駕駛汽車等領域都有著重要的應用。隨著物聯網和第五代通信技術發展迅速，互聯網中數據交換量不斷增大。據思科白皮書估計，到2022 年，移動設備的人均擁有數量將達到1.5 臺，移動設備將占全球IP 總流量的20%。當這些移動設備產生的數據都傳輸到核心云服務器并由其完成時，勢必導致網絡的擁塞。但MEC 的應用解決了這些問題。

MEC 通過協助完成移動設備的任務，可以減少移動設備完成這些任務的能耗和時延。然而，由于移動設備的功率有限，在節約能耗的同時提高其計算能力成為了一項挑戰。現今的研究通常關注利用邊緣服務器或遠程云，以提高移動設備的計算能力，比如利用邊緣服務器和云服務器來最小化總能耗或最小化任務完成時間。但是目前的這些研究大都沒有涉及多移動設備共存計算任務卸載場景下，移動設備能耗均衡保障問題。

多設備多任務的能耗均衡問題是最小化多個設備的最大能耗問題。假設有一個名為的邊緣服務器和兩個分別名為、的移動設備。為了簡化，假設移動設備、均存在兩個任務，這兩個任務均需要在兩個時間周期內完成。為簡化描述，假設邊緣服務器和移動設備在每個時間周期只能運行一個任務。此外，任務交付到邊緣服務器執行時，所產生的能耗代價更低。如果將中的兩個子任務都交付給，則無法再使用邊緣服務器，這導致設備的能耗顯著高于設備，顯然這是不均衡的。因此，為了達到能耗均衡，需要重新設計任務調度策略。

據了解，與本文研究最相似的文獻為文獻[12]和文獻[13]。其中文獻[12]的結構也是三層結構，同時考慮了任務的依賴關系，但其目標是最小化總能耗，沒有考慮移動設備能耗的均衡問題。并且該文章的結構由端邊云三者組成，也沒有考慮到使用中繼設備來優化系統。而文獻[13]的結構為多個原設備和一個由邊緣服務器集成的無線訪問接入點（wireless access point，AP）組成，研究的是兩個用戶下最小化加權能耗和。但該文獻也并沒有使用中繼設備，且該文獻中的任務是可以被隨意劃分的，任務之間不考慮依賴關系。

因此為了改進現有的工作，綜合上述文章，本文在原有的結構中去除了傳輸能耗更大的云服務器，加入了中繼設備節點作為任務的中轉節點，構成了一個由移動設備、中繼設備和邊緣服務器組成的三層結構。本文的貢獻點如下：

（1）基于上述結構設計了一種滿足任務依賴的多設備多任務能耗均衡貪心算法MMG（min-max greedy algorithm）。較之現存的最小能耗算法，MMG 算法在具有任務依賴關系的多設備多任務能耗均衡問題上具有更有效的表現。

（2）將能耗均衡問題轉化為最小化最大能耗問題，并且設計了總能耗優化算法以及隨機算法來與MMG 算法進行對比。

（3）為了驗證MMG 算法的優越性，進行了大量的對比實驗。實驗結果證明，MMG 算法的平均性能在能耗均衡方面可進一步提升66.59%。

1 相關工作

在MEC 的研究上，大部分的團隊集中于研究如何充分地利用服務器的資源以提高移動設備的性能。其目標一般分為兩種：節約能耗成本和減少任務完成時間。

在節約能耗成本上，文獻[14]設計了一個動態計算卸載算法和一個對應的在線卸載算法來解決動態計算卸載問題和節省移動設備能耗。文獻[15]提出了一種調度算法來分配無線帶寬，使所有用戶的總成本最小化。文獻[16]提出了兩種卸載策略，以最小化延遲約束下的能耗。文獻[17]提出了一種邊緣云架構，并設計了貪心算法來最小化移動設備的總能耗。文獻[18]設計了一種結合“0-1”編程和聯盟博弈并通過在移動用戶之間共享計算結果的分布式算法來最小化移動設備的總能耗。文獻[19]研究的是在一個由遠程云和異構本地處理器組成的體系結構中，在時間約束下最小化應用程序總執行成本問題。文獻[20]提出了一種分布式線性松弛啟發式算法和貪婪啟發式算法來最小化移動用戶的總能耗。文獻[21]考慮的是能耗問題和敏感型任務的調度策略問題，并設計了一種分布式動態卸載和資源調度策略，目標是最小化移動設備能耗，但沒有考慮設備間的能耗均衡問題。上述的這些文章都沒有充分考慮任務完成時間的問題，也沒有考慮利用中繼設備的協作作用來更好地優化移動設備的能耗。

在降低任務完成時間上，文獻[22]通過利用馬爾可夫決策方法，提出了一種高效的一維搜索算法，使每個計算任務的平均延遲最小化。在多用戶多任務問題上，文獻[23]設計了集中式分布式貪心最大調度算法，解決了多用戶多任務計算卸載問題，但文章沒有考慮任務依賴關系。文獻[24]提出了一種“邊緣-云”協作的“依賴-感知”卸載方案，并設計了兩種算法，解決的是在任務依賴約束和給定預算的情況下最小化設備任務完成時間。文獻[25]假設邊緣服務器的資源無限大，研究不同移動用戶隨機到達的異構延遲敏感計算任務環境下，使移動用戶在任何給定的計算卸載策略下的總時延最小問題，并將該問題建模成一個動態優先隊列，同時設計了一種優先傳輸調度策略來解決。然而上述文章也都沒有考慮使用中繼設備。

除能耗和任務完成時間外，也有一些研究致力于解決邊緣計算所遇到的其他難解問題。文獻[26]利用博弈論設計了一種分布式計算卸載算法，研究了多信道無線干擾環境下的多用戶卸載問題。文獻[27]利用進化博弈策略來研究動態環境下的多用戶計算卸載問題。文獻[28]利用無人機的移動性來解決邊緣服務器的低移動性問題。

2 模型

本章將會先介紹本文系統的模型。本文所使用到的符號及其含義如表1 所示。

表1 本文所用符號Table 1 Notations of this paper

2.1 系統模型

如圖1 所示，系統是一個具有三層架構的移動邊緣計算模型。系統的頂層位于一個具有計算能力的邊緣服務器上，而這個服務器一般位于基站或遠程訪問點。系統的中間層為中繼設備，它們只負責任務傳輸但不負責任務的執行。系統底層是移動設備，每個移動設備都有一個正在運行的應用程序，每個應用程序由多個具有任務依賴關系的子任務組成。

圖1 系統模型Fig.1 System model

移動設備通過無線連接的方式與中繼設備進行通信，如Wi-Fi 等。中繼設備也通過無線連接與邊緣服務器通信。模型中存在多個移動設備，用集合M={,,…,m}表示，其中是移動設備的數量。此外，模型中的中繼設備用集合H={,,…,h}表示，其中是中繼設備的數量。對于每一個移動設備,都包含個有依賴關系的子任務，用N={,,…, n}表示。

以下，將詳細介紹本文的通信模型和計算模型。

2.2 無線通信模型

無線通信存在于移動設備和中繼設備以及中繼設備和邊緣服務器之間。根據香農公式，從第個移動設備到第個中繼設備之間的上行數據速率可以表示為：

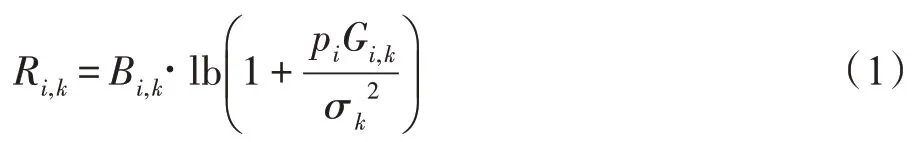
類似地，第個中繼設備與邊緣服務器之間的上行數據速率為：

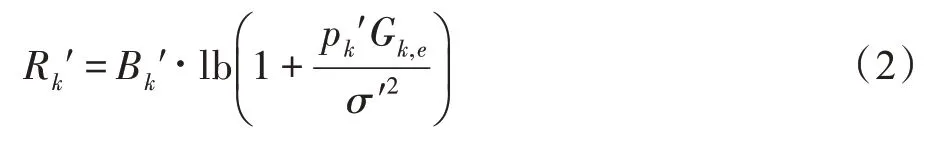
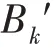
其中，d為節點與之間的歐式距離，為路徑損失分量，且,∈{M ?H?{}}。

2.3 計算模型

當中的在移動設備本地執行時，其執行時間可以表示為：

其中，W是完成第個移動設備中的第個子任務所需要的工作量大小，f是第個移動設備的CPU 時鐘周期頻率，單位為cycle/s，對應的能耗可以表示為：

其中，ρ為取決于移動設備架構的一個正常數。如果第個移動設備中的第個子任務被卸載到第個中繼設備時，此階段的傳輸時間可以表示為：

其中，D為第個移動設備的第個子任務的數據量大小。這個過程的能耗可以表示為：

如果第個移動設備中的第個子任務從第個中繼設備被卸載到邊緣服務器，此過程的傳輸時間可以表示為：

對應的能耗為：

在邊緣服務器上完成第個移動設備的第個子任務的計算時間為：

其中，f為的CPU 時鐘周期頻率，單位為cycle/s。

因此，完成第個移動設備的第個子任務的能耗為：

2.4 任務依賴性

本節定義了子任務之間的依賴關系。子任務的完成時間分為以下幾部分。

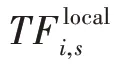
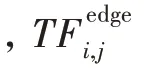
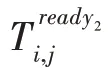
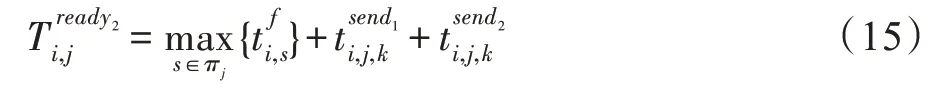
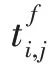
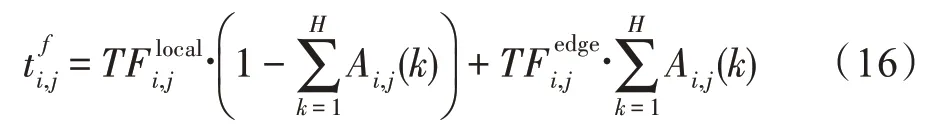
因此，第個移動設備完成所有子任務所需要的時間為：

綜上所述，第個移動設備的總能量消耗可以表示為：

2.5 問題定義

本節將給出最小化最大能耗問題的公式化定義。最小化最大能耗問題描述如下：

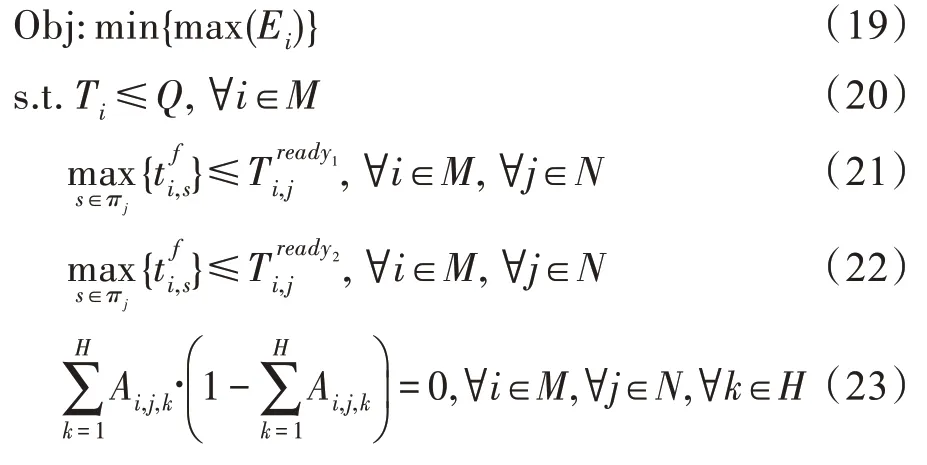
其中，為給定的第個移動設備完成所有子任務的預算時間。式（20）是對第個移動設備的完成時間的約束。式（21）和式（22）是子任務的依賴性約束，確保第個移動設備的第個子任務只能在其所有前驅子任務完成后才能開始執行。式（23）表示第個移動設備的第個子任務只能在本地執行或者在邊緣服務器執行。

據現有的研究可知，最小化最大能耗問題是一個找尋調度策略的優化問題，可以規約為文獻[29]中的最小化最大時間問題，而該文獻將最小化最大時間問題規約為NP-hard 整數規劃問題。因此，最小化最大能耗問題為NP-hard。

3 算法設計與分析

本章對提出的MMG 算法進行詳細描述。

本文根據子任務的數量將劃分為幾個部分，并且每一層的每個子任務都應該在劃分完成之后的區間結束。對于每個子任務，根據時間和能耗條件確定計算模式。然后，對于每個子任務，通過最小-最大算法來獲得分配方案。此外，再判斷分配方案是否滿足時間限制。

在以上分析的基礎上，首先，通過計算獲得不同子任務在本地計算、遷移到邊緣服務器計算的能耗，并形成一個能耗矩陣。對于每一個移動設備源節點，都隨機分配一個中繼設備節點。假設是源節點到中繼的最大能耗，找到并將所有中繼設置為“unused”，當中繼設備被占用時設置為“used”。獲取分配策略。逐個判斷最大能耗所分配的中繼設備節點之外是否有其他中繼設備節點可用。若可用，則更換中繼設備節點，確定新的（調整能耗使得分配策略所得的總能耗在盡量小的情況下能耗差更小）。若未找到其他可用中繼設備節點，則開始判斷分配策略是否滿足時間約束，若不滿足，則重新分配策略；若滿足，則獲得可行分配策略。

設定移動設備的數量為，每個移動設備的子任務數量為，中繼設備的數量為。算法的總時間復雜度為(+)。

首先，本文提出的算法分三層嵌套循環來計算時間消耗和能量消耗，其時間復雜度為()。然后，分析了最小-最大函數的時間復雜度。每次迭代的復雜度為()，每次迭代最多有對，因此最小-最大的總時間復雜度為()。在時間檢查方面，這是一個只有一層循環的sum 函數，包括兩層嵌套的While 循環，每個While 循環不超過次，因此其時間復雜度為()。此外，第二步是在不同的子任務層下執行的，因此第二步的總時間復雜度為()。該算法的總時間復雜度為(+)。

任意移動邊緣計算結構的二部圖都可以轉化為能量消耗矩陣。將和分別表示為一個任意小的正常數和子任務數，則該貪心算法的近似比可以達到(1+)。

在定理1 中，分析得到算法的時間復雜度為(+)，其最大的迭代次數為。對于一個子任務而言，根據式（7）、式（9），分別令其傳輸能量比為和；根據式（5），令其計算能量比為。每個“設備-中繼”對的能耗可以表示為E=min(σ+γ, ψ)。“源-中繼”的最大和有效最小能耗分別設為和。則有：

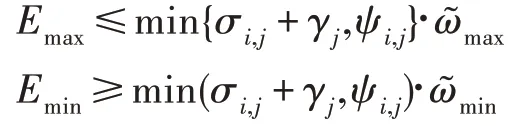
其中

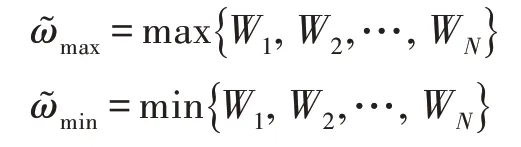
因此，每個“設備-中繼”對的能量消耗上界為。設=/，其中為每個“設備-中繼”對最大能耗平均調整的步長，是迭代的最大次數，則有=/。設()為最小化每個“設備-中繼”對的最大能耗的最優解，其中對應的最優策略。設′為貪心算法中每個“設備-中繼”對的最大能耗，則有()≤(′)。又=/，則有=。因此，是其中一個移動設備能耗調整的上界。據此，則有：根據式（24）和0 ＜＜()，有：

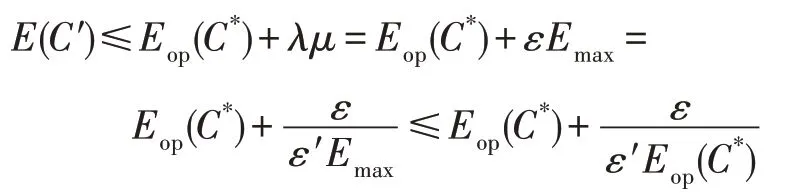
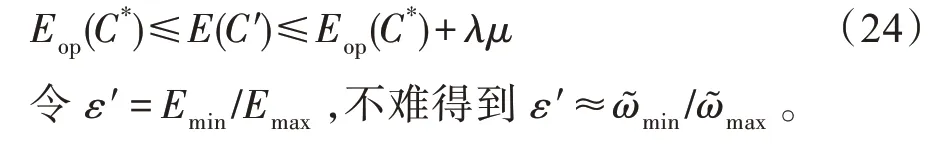
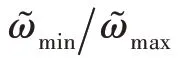
本文所提出的貪心算法偽代碼如下所示：

Min-max greedy algorithm(MMG)

輸入：工作量大小，數據量大小，時間約束。

輸出：分配策略。

Min-max algorithm

輸入：子任務數量的級別，能量消耗矩陣。

輸出：分配策略。

1.for(,) in listdo

2.檢查中繼節點的可用性

3.if(,) is availability then

4.將源節點的對移除

5.將(,)對分配給源節點

6.回到第二行來確定一個新的

7.if no pair availability then

8.算法結束

4 性能評估

本章設計了實驗來研究所提出的算法的性能。本文利用Matlab r2016a 進行了大量的實驗，并得到了實驗結果。

文中將覆蓋范圍設定為50 m×50 m。默認情況下，子任務、移動設備和中繼設備的數量分別設置為4、3和3，實驗中的其他參數如表2所示。在整個實驗過程中，文章假設計算任務的數據大小、工作量大小在[25 Kbit,1 024 Kbit]范圍內遵循正態分布，平均值為512，標準差為256。此外，本文還設計了一個總能耗優化算法（total energy consumption minimization algorithm，TECM）的實驗對比算法。

表2 實驗參數Table 2 Experimental parameters

在實驗1 中，文章研究了路徑損耗分量與子任務最大能量消耗之間關系的變化。圖2（a）描述了子任務的最大能量消耗隨著路徑損耗分量的增加而增加。從式（1）、（2）、（3）、（6）、（8）中得出，子任務的最大能量消耗與路徑損耗分量成正比，這解釋了實驗圖2 中的曲線形狀。實驗表明，當移動設備的傳輸功率分別為5 dBm 和6 dBm 時，MMG 算法在最小化子任務的最大能耗方面的性能平均比隨機算法提升66.59%和61.87%，接近蠻力算法得到的最優解。圖2（b）基于圖2（a）的結果，結果表明，當移動設備的最小傳輸功率分別為5 dBm 和6 dBm 時，MMG 算法的近似比分別為1.096 9 和1.098 4。

圖2 實驗1Fig.2 The first experiment

實驗2 研究了子任務在時間約束變化下的最大能量消耗。在圖3（a）和圖3（b）中，移動設備的最小傳輸功率為5 dBm。結果表明，貪心算法的性能優于總能耗優化算法和隨機算法。

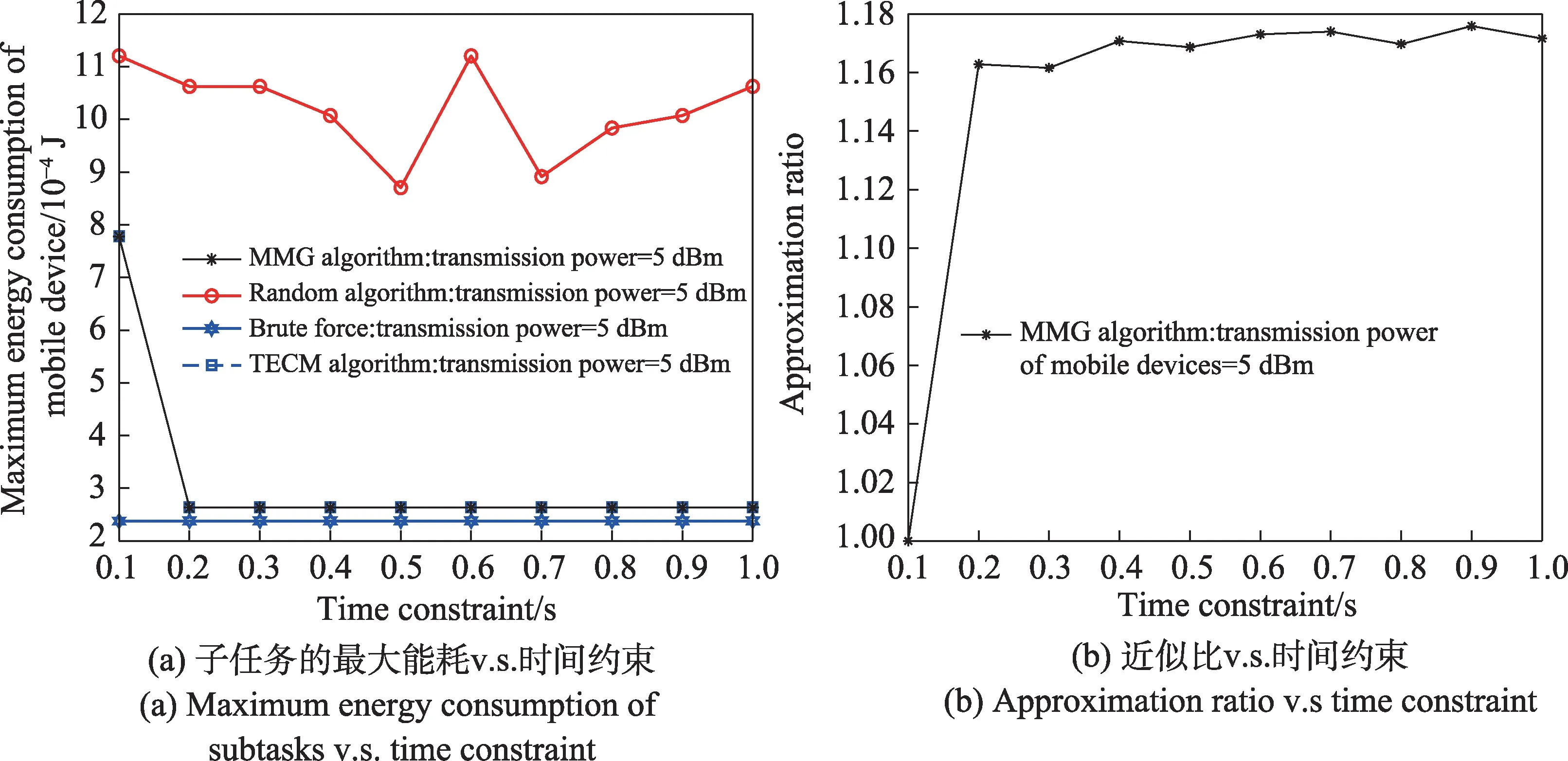
圖3 實驗2Fig.3 The second experiment

最后，在路徑損耗分量為0.1 的情況下，文章觀察了子任務的最大能量消耗隨任務層數的變化。如圖4（a）所示，隨著任務數量的增加，每個子任務的完成時間相應地減少，從而導致任務需要在更短的時間內執行。這導致完成任務所需的能量消耗增加。但是MMG 算法在最小子任務的最大能耗的性能上明顯優于TECM 算法和隨機算法。如圖4（b）所示，隨著子任務數的增加，子任務的最大能量消耗增加，當移動設備的傳輸功率分別為5 dBm 和6 dBm 時，MMG 的近似比分別為1.353 7、1.353 8。

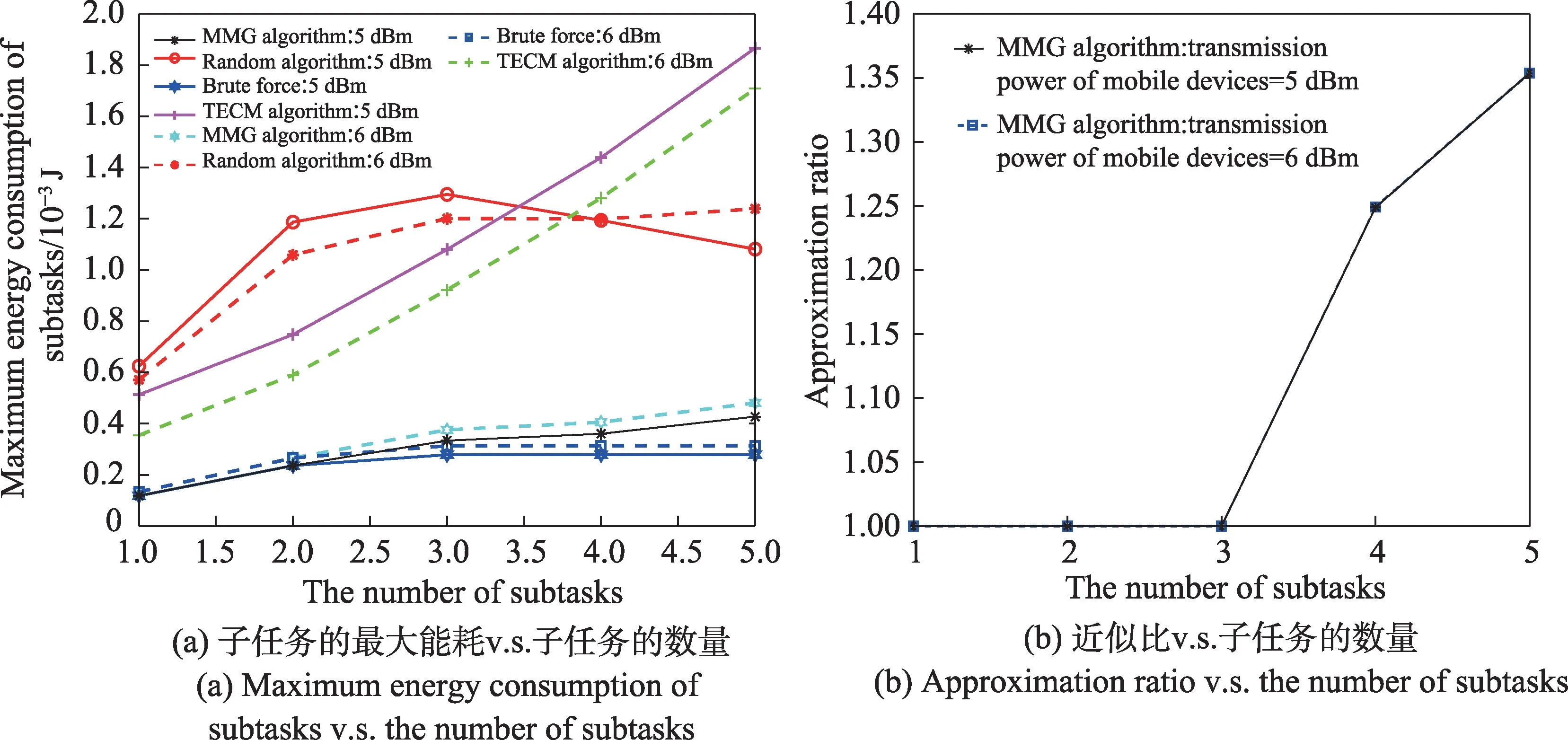
圖4 實驗3Fig.4 The third experiment

5 結束語

本文研究了多移動設備多任務中的能耗均衡問題，這個問題是NP-hard。文章在原有的結構中去除了傳輸能耗更大的云服務器，加入了中繼設備節點作為任務的中轉節點，構成了一個由移動設備、中繼設備和邊緣服務器組成的三層結構。同時本文設計了MMG 算法來求解能耗均衡問題，并通過大量的對比實驗證明了MMG 算法的有效性。