基于生成對抗網絡的塔里木深層超深層疊前地震子波提取

韓浩宇，戴永壽*，宋建國，萬勇，孫偉峰，李泓浩

1 中國石油大學(華東)海洋與空間信息學院，青島 266580 2 中國石油大學(華東)地球科學與技術學院，青島 266580

0 引言

在地球物理勘探領域中，全波形反演技術與疊前偏移成像等技術對儲層分布、地層巖性構造有著重要意義，而這些技術的準確度離不開疊前地震子波的準確提取.傳統地震子波的提取主要依靠頻譜分解方法，Rosa和Ulrych(1991)提出一種譜模擬反褶積的方法，該方法從地震記錄振幅譜中得到地震子波振幅譜，通過壓縮地震子波提高地震資料的分辨率.Wang等(2015)提出了基于蟻群算法的子波相位估計方法，通過對子波振幅譜進行希爾伯特變換得到最小相位子波并將最小相位子波Z域的零點關于單位圓進行對稱變換，建立候選子波庫，最后利用蟻群算法實現子波相位的準確尋優.我國西部的塔里木盆地具有豐富的石油資源，也是我國油氣勘探的重要戰略地區.塔里木盆地含有巨厚膏巖體以及熔斷體等復雜地質結構；儲層位于地下深層超深層；地震資料信噪比低，有效信號微弱.因此，塔里木地區疊前地震子波提取難度更高，同時也具有重要的研究價值.傳統地震子波提取方法無法快速準確地完成塔里木地區疊前地震子波提取的工作，更快速高效的子波提取方法研究及其應用迫在眉睫.

生成對抗網絡(GAN，Generative Adversarial Nets)是由Goodfellow等(2014)提出的一種神經網絡模型，在自然圖像、語音、文本等方面取得廣泛應用.生成對抗網絡相較于傳統卷積神經網絡(CNN，Convolutional Neural Network)具有以下改進：(1)在處理一維地震數據的情況下，GAN算法可以不受CNN的分類標簽限制；(2)GAN網絡結構由雙CNN嵌套構成，網絡結構更加復雜，交叉訓練更加準確；(3)在算法邏輯上，GAN只采用反向傳播算法而不采用馬爾科夫鏈，不需要對數據隱變量進行推斷.由于GAN的結構優勢，近年來該算法被逐步應用于地震數據處理領域中.Li和Luo(2019)利用GAN數據增強的特性對原始地震剖面圖進行訓練，獲得更高分辨率的地震剖面圖以實現高分辨率地震反演.Kaur等(2019)通過CycleGAN對地震數據的原始分布進行訓練，完成了對缺失地震道記錄的插值工作.Mao等(2019)利用GAN實現了滾動軸承不平衡性的故障診斷，首先利用GAN的鑒別器判斷滾動軸承參數序列的準確性，然后生成器擬合無故障情況下的軸承參數序列，驗證了生成對抗網絡處理一維序列的有效性.這些GAN算法的應用為本文實現疊前地震子波的提取提供了可能.

本文通過采用生成對抗網絡來實現疊前地震子波的提取.針對塔里木地區的深層低信噪比疊前地震資料，通過去噪等方式實現數據預處理，利用傳統地震子波提取方法提取部分地震資料中的疊前地震子波，再與合成疊前地震記錄共同組成訓練集；采用生成對抗網絡訓練數據集，最后利用地震子波與地震記錄的概率分布特征不同實現疊前地震子波的處理，從而降低運算復雜度.

1 基于生成對抗網絡的疊前地震子波提取方法

生成對抗網絡中的生成器與鑒別器的輸入分別為疊前地震記錄與疊前地震子波，用于訓練的數據集則是由針對塔里木地區的合成數據所建立.本節從生成對抗網絡提取地震子波的原理流程及疊前地震子波樣本集兩個方面進行詳細描述.

本節內容從生成對抗網絡算法原理和疊前地震記錄及對應用于合成的地震子波的樣本集建立兩個方面進行詳細描述.

1.1 生成對抗網絡地震子波提取基本原理和流程

依據地震褶積模型的理論，地震記錄可以被表示為地震子波與反射系數的褶積：

x(t)=w(t,τ)*r(t)+n(t)，

(1)

其中x(t)代表地震記錄，w(t,τ)代表地震子波，r(t)代表反射系數，n(t)代表噪聲，*代表卷積運算.在噪聲及反射系數未知的情況下，地震子波的求解過程可以被視為非線性最優化求解問題，可由公式(2)表達：

(2)

其中Xn(t)代表地震記錄，wΔ(t)代表估計地震子波.對于式(2)而言，由于反射系數與地震子波都是未知量，所以直接求解無疑是非常復雜的.為優化求解過程，從疊前地震記錄中準確提取地震子波，本文提出了一種基于數據驅動的生成對抗網絡的方法實現地震子波的提取.

生成對抗網絡是近年來興起的一種深度學習算法，其應用場合十分廣泛.本文中對生成對抗網絡進行了適用性改進，使其能夠更準確的完成子波提取工作.該網絡主要由兩部分構成：生成器和鑒別器，其中，生成器主要作用是：從地震記錄中估計地震子波.鑒別器主要作用為：判斷估計子波的準確性.利用生成器與鑒別器之間地相互博弈，實現疊前地震子波的準確提取及準確性評價.基于生成對抗網絡的子波提取處理過程如圖1所示.

本文以1×n的合成疊前地震記錄作為生成器的輸入，以用于合成相應記錄的疊前地震子波作為鑒別器輸入樣本.鑒別器與生成器包含了卷積層(CONV)、下采樣層(Sub-Sampling)、反卷積層(CONV_tran)與全連接層(Fully-Connect).網絡搭建完成后，初始模型通過不斷的迭代訓練直至獲得預期模型.

1.2 生成對抗網絡結構與網絡訓練過程

生成對抗網絡中的生成器與鑒別器都由卷積神經網絡構成，網絡首先進行鑒別器訓練.鑒別器主要任務是學習疊前地震子波的數據特征，其本質是二分類器.我們將輸入的地震子波訓練樣本標記為1，即真實子波，將初始生成器的輸出值標記為0，即偽子波.而生成器則是一個僅包含前向傳播算法的卷積神經網絡，其網絡參數更新則由鑒別器傳遞更新.網絡具體結構如圖2所示.

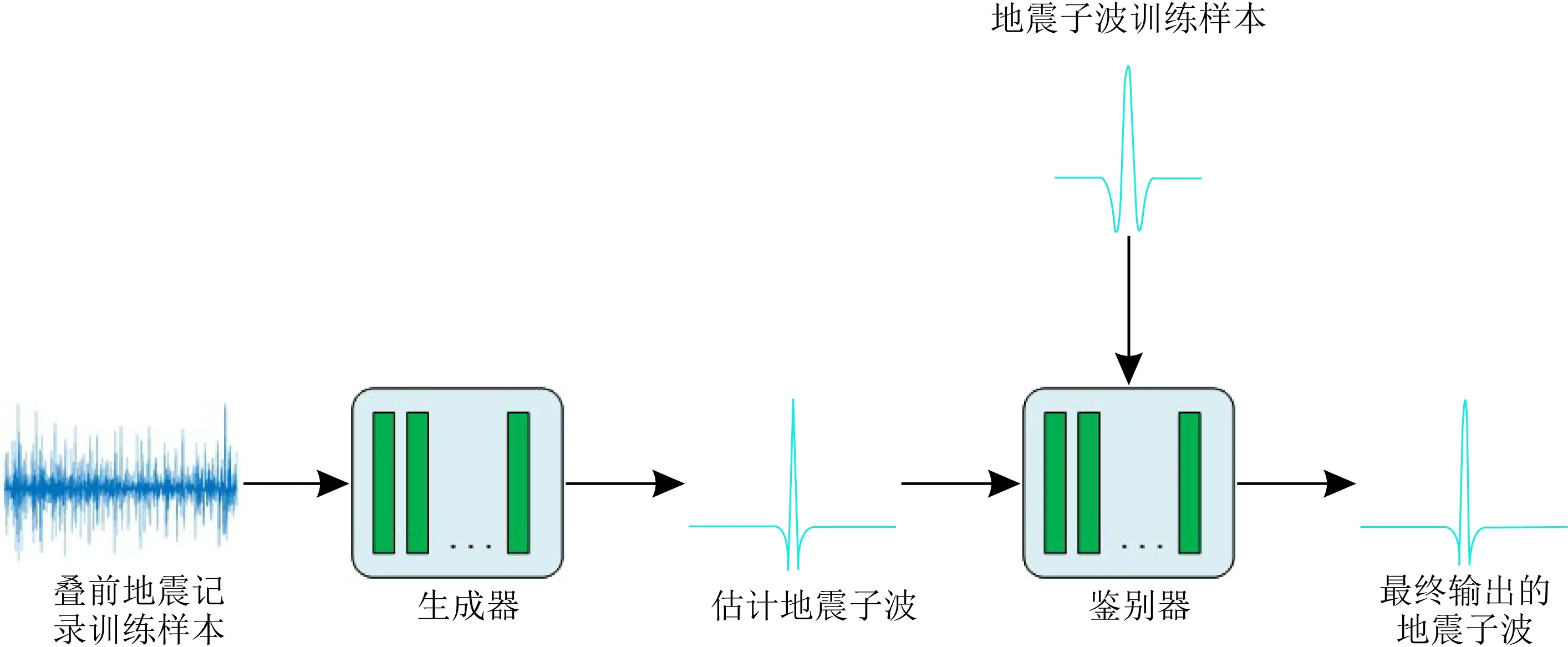
圖1 基于GAN算法的子波提取處理流程圖Fig.1 Wavelet extraction processing flow chart based on GAN

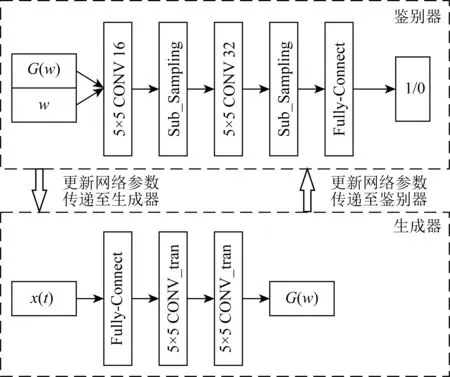
圖2 生成對抗網絡結構圖Fig.2 Generative Adversarial Networks structure diagram

圖2中G(w)代表生成器生成的估計子波，w代表真實地震子波，x(t)代表疊前地震記錄.本文所采用的生成對抗網絡中生成器共由五層網絡構成，包含兩層卷積層、兩層下采樣層和一層全連接層，鑒別器則由三層網絡構成，包含一層全連接層及兩層反卷積層.

GAN每次訓練都會將訓練集當中的疊前地震子波與生成器生成的估計子波交替輸入至鑒別器網絡，通過卷積層提取數據特征，再通過下采樣層對特征數據進行降維，防止過擬合情況出現，最終輸出32個特征圖集.以特征圖集為鑒別條件，疊前地震子波特征標記為1(真實子波)，而生成子波則通過損失函數誤差判別為0(偽子波)與1(真實子波)的中間值.若判定結果大于0.5則認為生成子波即為疊前地震記錄所對應的真實地震子波.

考慮到地震數據的特殊性以方便神經網絡處理，首先需要先對地震數據進行預處理.在實驗過程中發現，由于地震記錄與地震子波振幅數據中含有大量負值，而網絡卷積訓練過程中受卷積核運算及激活函數影響，負參數可能導致節點死亡，訓練結果不準確.參考深度學習在圖像處理中的應用特點，我們對地震數據歸一化至[0,1]區間內.歸一化公式為：

(3)

其中Xnorm代表歸一化后的地震數據.該方法可將原始數據等比例縮放.

將預處理后1×500的地震子波數據通過卷積層與下采樣層提取特征數據，該過程主要通過卷積核運算獲得高維度數據特征.卷積層計算過程為：

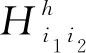
(4)

其中?是二維卷積算子，σ是激活函數，Wh是網絡權重參數，初始化為較小的隨機數，bh是網絡偏置值，初始化為0.

激活函數可提高模型的非線性擬合能力.標準GAN中常采用sigmoid或tanh函數作為激活函數，通過對地震數據的特性分析及實驗結果驗證，將激活函數替換為帶泄露修正單元leaky ReLUs.Leaky ReLUs函數改進自ReLUs函數(Nair and Hinton，2010)，屬于神經網絡當中常用激活函數之一，其優勢在于可以使網絡的收斂速度更快，且避免輸入特征數據存在負值時網絡偏置無法更新.激活函數公式為：

(5)

其中xi為輸入特征值，ai是常數參數.在網絡的不斷訓練過程中網絡權重參數與偏置值也會不斷更新.

卷積層輸出的高維度數據特征不僅會使得數據冗余，網絡訓練速度緩慢，且網絡學習過多特征會導致訓練結果不準確.而下采樣層的主要作用即對特征數據進行降維，保留攜帶位置信息且相關性強的特征數據，舍去多余特征數據，其主要原理借鑒了圖像的下采樣過程.

最后通過卷積層與下采樣層的特征數據通過全連接層后，輸入至損失函數進行誤差判別，這一步驟決定著鑒別器的鑒別結果.生成對抗網絡與傳統卷積神經網絡所不同的是利用了JS散度作為損失函數進行誤差判別.損失函數公式為：

(6)

(7)

其中Pg(w)代表生成器生成的估計子波的概率分布，Pr(w)代表真實子波的概率分布，KL則代表KL散度，其表達式如公式(6)所示.鑒別器依據損失函數更新網絡參數，當生成樣本與真實樣本具有較大偏差時，損失函數能夠提供較大梯度，網絡沿梯度下降方向更新網絡參數同時將更新后的參數傳遞至鑒別器與生成器中.需要我們注意的是，隨著不斷訓練，鑒別器對子波真實性的鑒別能力不斷增強，最終達到最優鑒別器.

在鑒別器不斷訓練的過程中，生成器也在不斷進行訓練與優化.生成對抗網絡的訓練過程是交叉訓練的.生成器不包含反向傳播算法，其網絡參數更新依賴于鑒別器的誤差反向傳播算法.生成器每次參數更新后，都會從新一組的疊前地震記錄中生成估計子波.生成器類似于逆向的卷積神經網絡，疊前地震子波輸入至生成器后通過全連接層后轉化為網絡數據特征，具體形式可類比鑒別器中子波數據通過卷積層后所得到的數據特征.此時將生成器從疊前地震記錄中所獲得的數據特征通過反卷積層進行數據重構，同樣經過兩層反卷積層后獲得重構的估計子波G(w).反卷積層的具體公式為：

w=(d-1)×s+k，

(8)

其中w代表生成子波，d代表全連接層轉化后的特征值，s則代表滑動步長，本文步長設置為2，k代表卷積核大小，本文設置為5.

在網絡框架搭建完成后，為實現深層疊前地震子波的準確提取，我們期望通過生成器生成的地震子波能夠不斷的逼近疊前地震記錄中的真實子波：

J=min(G(w)-w)2，

(9)

其中G(w)代表生成器生成的估計子波.為了使式(9)中J取值盡可能逼近0，將生成網絡的目標函數設置為：

minGmaxDV[D,G]=Ew[lgD(w)]

+E′w[lg(1-D(G(w′)))]，

(10)

其中，D(w)代表最優鑒別器，D(G(w′)代表最優鑒別器對生成器生成的估計子波的鑒別結果.生成對抗網絡主要學習數據的概率分布特征，該目標函數用于衡量生成子波與真實子波之間分布相同程度.從目標函數中可以看出，對于一個固定的生成器G而言，鑒別器D需要不斷提高鑒別能力，即最大化兩者之間的交叉熵，從而準確區分生成樣本與真實樣本的區別，對于一個固定的鑒別器D而言，則需要不斷提升生成器G所生成樣本的準確性，使得D難以區分兩者區別.兩者之間的在學習過程中是不斷對抗與博弈的，其學習過程(Goodfellow et al.，2014)如圖3所示.

圖3中Z到X的映射過程代表了生成樣本向真實樣本的映射過程.圖3a代表網絡初始訓練階段，鑒別器性能不足，生成數據與真實數據偏差較大；圖3b代表鑒別器再經過一定訓練后已獲得較強的鑒別能力，能夠初步區分生成樣本與真實數據之間的差異；圖3c代表鑒別器不斷引導生成器生成數據向真實樣本的概率分布移動；圖3d代表訓練完成階段，鑒別器已無法區分生成數據與真實數據之間差異的階段.從圖3a—d代表著生成對抗網絡不斷迭代學習直至達到預期結果的過程.

對于鑒別器而言，鑒別函數越大則能更準確地給出輸入樣本中真實樣本的比例，也意味著提取得到的結果地震子波更加接近真實子波，最優鑒別器D(w)通過公式(11)和(12)迭代獲得：

互聯網時代為人類提供了許多的可能，企業也可以搭上這趟便車(順勢利用互聯網的及時性)為會計職業風險的防范提供良好的保障，即利用互聯網對企業財務工作進行實時監督。

(11)

(12)

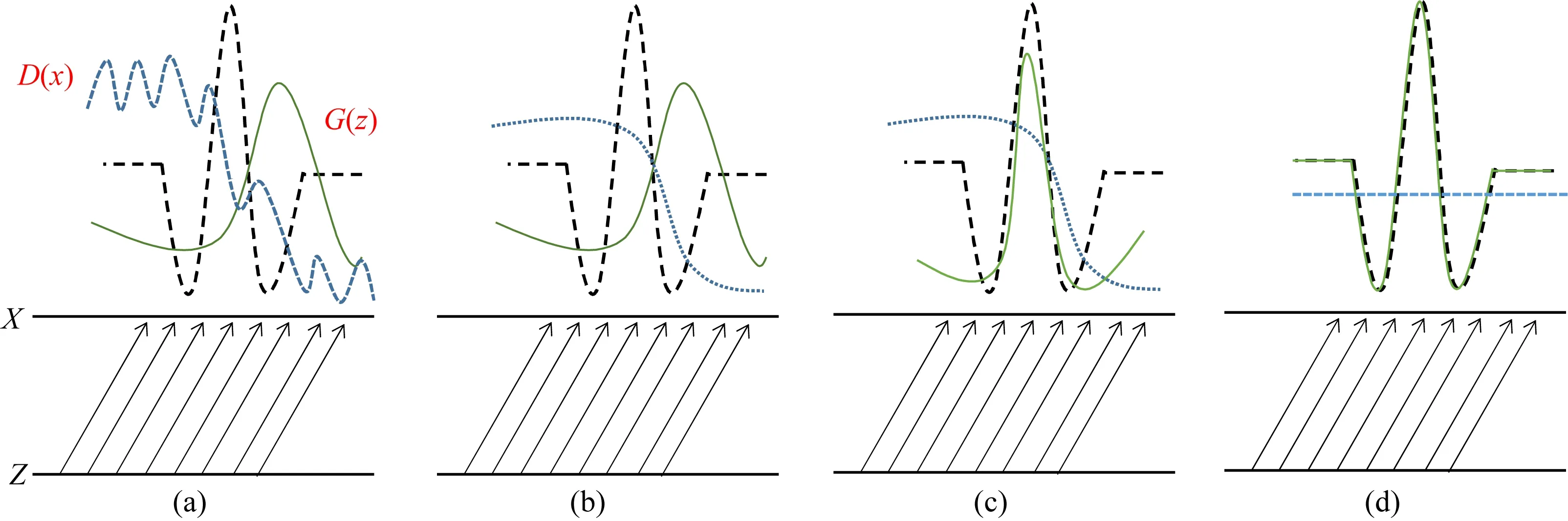
圖3 生成對抗網絡的學習過程圖(a) 網絡初始學習階段示意圖； (b) 鑒別器學習示意圖； (c) 生成器學習示意圖； (d) 網絡訓練完成階段示意圖.Fig.3 Diagram of the learning process of generating a confrontation network(a) Schematic diagram of the initial learning stage of the network; (b) Schematic diagram of the discriminator learning; (c) Schematic diagram of generator learning; (d) Schematic diagram of completion stage of network training.

其中D′(w)代表最優鑒別器的導數，Pr(w)代表真實地震子波樣本的概率分布，Pg(w)代表假樣本的概率分布.整個網絡的訓練過程中，生成器輸出的估計子波與真實子波在鑒別器中不斷地進行特征匹配，通過生成器與鑒別器之間的博弈，使估計子波不斷向真實子波收斂.當生成對抗網絡到達納什平衡(Goodfellow et al.，2014)時，即達到鑒別器無法區分估計子波與真實子波的時刻，認為最后一次迭代中生成器所生成的結果子波即為對應疊前地震記錄中的真實地震子波.

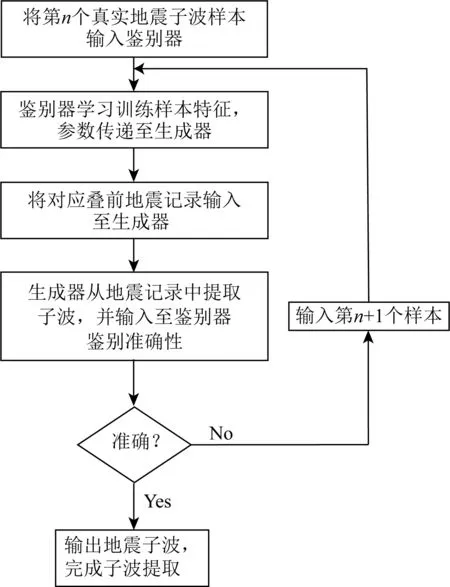
圖4 生成對抗網絡的訓練流程圖Fig.4 The training flowchart of the confrontation generation network

整個生成對抗網絡的訓練過程是生成器與鑒別器交替進行的，具體過程如圖4所示.在基于生成對抗網絡的地震子波提取方法中，最重要的步驟為疊前地震子波及其對應疊前地震記錄樣本集的建立，由于本文方法針對目標區域為塔里木柯東地區，所以樣本標簽集需針對目標靶區特性人工建立.

1.3 生成對抗網絡訓練集地構建

由于用作生成對抗網絡訓練樣本的疊前地震子波的完備性和疊前地震記錄的特征相似度決定了生成對抗網絡求解的疊前地震子波的準確性，因而本文有針對性地建立了柯東地區疊前地震記錄及對應的地震子波樣本集，用于生成對抗網絡進行訓練.

樣本集是一個帶標簽的數據集，包含了網絡的輸入與輸出數據，在生成對抗網絡中，利用疊前深層地震記錄取代隨機噪聲信號作為輸入，用于合成的對應疊前地震子波作為網絡輸出.本文所建立的柯東地區疊前地震記錄及對應地震子波樣本集由合成地震記錄組成，分別采用國際主流地震速度模型—Marmousi模型和鹽丘模型與不同主頻和幅度的雷克子波進行正演合成無噪的疊前地震記錄，并為地震記錄加入隨機噪聲，保證合成記錄的信噪比與實際地震資料一致性.合成疊前地震記錄流程如圖5所示.

圖5 疊前地震記錄合成流程圖Fig.5 Flow chart of pre-stack seismic record synthesis

地震記錄正演結果如圖6所示.此時獲得的疊前地震記錄并不含噪聲，為更好地模擬塔里木地區深層超深層疊前地震記錄，對柯東地區地質構造及噪聲類型進行了簡要分析.柯東地區構造帶總體表現為典型的三角帶構造(被動頂板雙重構造)(曾昌明等，2011)，此外還具有明顯的斷層高陡特點(杜治利等，2013)和野外勘探中存在的惡劣環境，疊前地震數據噪聲十分強烈.為更好地擬合柯東地區疊前地震噪聲，采用傳統BM3D去噪方法對實際柯東疊前地震記錄進行噪聲去除，并將獲取到的多道噪聲添加至合成地震記錄當中，使樣本訓練集更加符合實際地震資料.

為更好地模擬目標區域疊前地震記錄，采用了不同類型及不同主頻的地震子波作為初始子波合成疊前地震炮記錄，并在合成后隨機添加不同信噪比的噪聲，建立了總量為20000個的樣本集.完成初始樣本集建立后，利用該樣本集進行網絡訓練，仿真與實測數據實驗詳見第2節.

2 數值實驗

為驗證基于生成對抗網絡算法的疊前地震子波提取方法的有效性及準確性，本文分別利用合成數據與柯東地區實際地震資料進行數值實驗.

2.1 合成地震記錄仿真實驗及結果分析

圖6 正演合成疊前地震記錄結果圖(a) Marmousi速度模型； (b) 合成疊前炮記錄； (c) 用于合成疊前地震記錄的雷克子波； (d) 合成疊前地震記錄(第1道).Fig.6 The result of forward synthetic pre-stack seismic record(a) Marmousi velocity model； (b) Synthetic prestack shot record； (c) Rick wavelet used to synthesize pre-stack seismic records； (d) Synthetic pre-stack seismic records (Track 1).

本文選取零偏移距疊前地震記錄進行方法準確性對比實驗.從實驗結果中分析可發現，傳統譜模擬算法及變分模態分解法在疊前地震子波提取中都存在不可忽視的旁瓣，在多次實驗中都存在相應問題，且需要不斷人工修改參數，提取過程復雜.子波提取結果與提取誤差如圖7和圖8所示.

表1 傳統譜模擬算法與生成對抗網絡算法的疊前地震子波提取速度對比Table 1 Comparison of pre-stack seismic wavelet extraction speed between traditional spectrum simulation algorithm and GAN

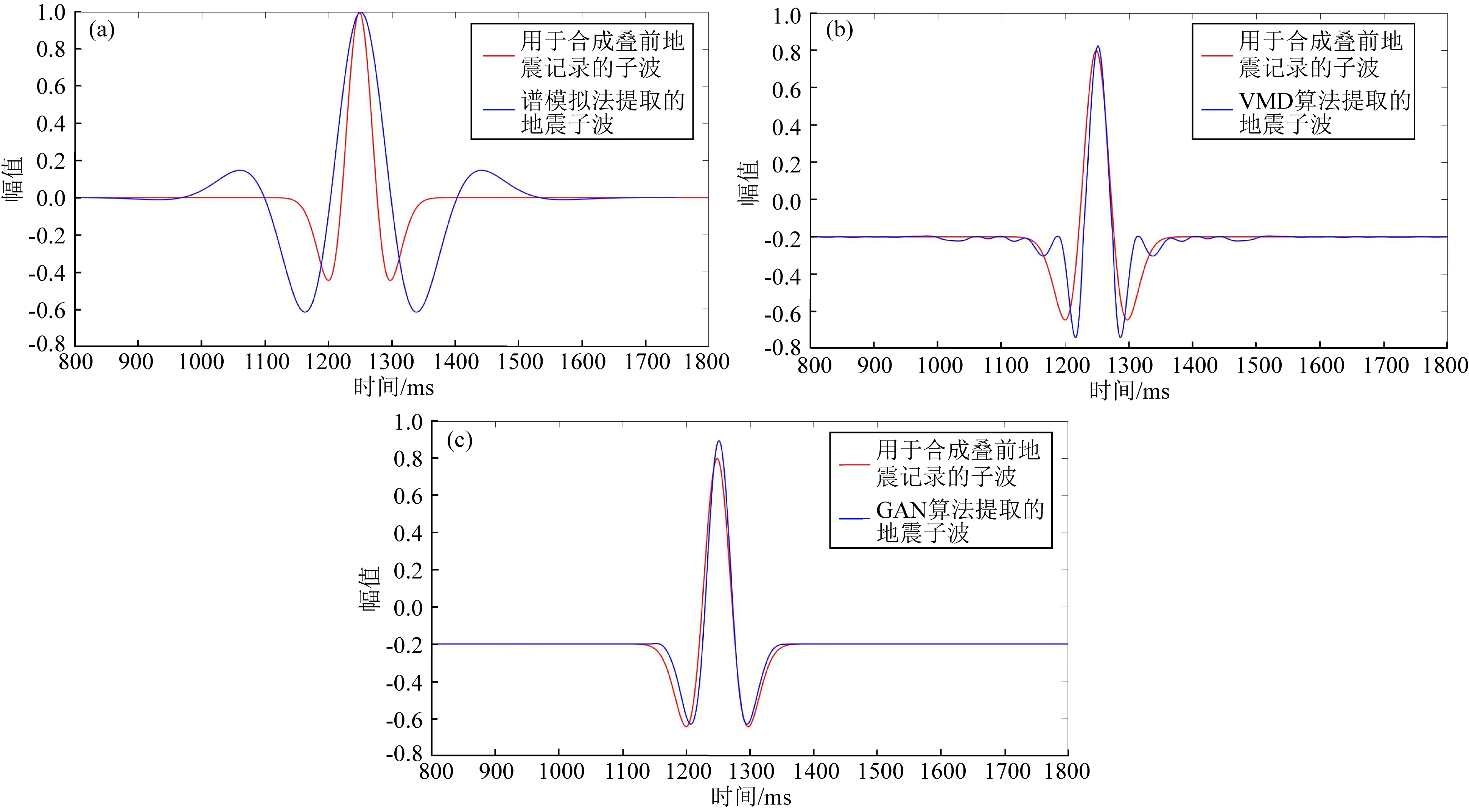
圖7 疊前地震子波提取結果對比(a) 譜模擬算法提取子波與合成子波對比； (b) VMD算法提取子波與合成子波對比； (c) 對抗生成算法提取子波與合成子波對比.紅色代表用于合成疊前記錄的雷克子波；藍色代表不同方法提取的疊前地震子波.Fig.7 Comparison of pre-stack seismic wavelet extraction results(a) Comparison between wavelet extracted by spectral simulation algorithm and synthesized wavelet； (b) Comparison between wavelet extracted by VMD algorithm and synthesized wavelet； (c) Comparison between wavelet extracted by GAN and synthesized wavelet. Red represents the Rick wavelet used to synthesize pre-stack records；Blue represents the pre-stack seismic wavelets extracted by different methods.

圖8 不同方法子波提取誤差對比(a) 傳統譜模擬算法的子波提取誤差； (b) 變分模態分解法的子波提取誤差； (c) 本文方法的子波提取誤差.Fig.8 Wavelet extraction errors comparison of different methods(a) Wavelet extraction error of traditional spectrum simulation algorithm; (b) Wavelet extraction error of variational modal decomposition method; (c) Wavelet extraction error of the method in this paper.

本文采用均方誤差對三種地震子波提取方法進行了誤差分析，其中傳統譜模擬算法的均方誤差MSE=0.0497，變分模態分解法的均方誤差MSE=0.0098，而本文中生成對抗網絡算法的均方誤差MSE=0.000571.實驗結果表明，本文所提出的基于生成對抗網絡的塔里木深層超深層疊前地震子波提取方法相比傳統算法更加準確.此外，通過針對不同目標區地層特性構建疊前地震子波訓練集，生成對抗網絡也可實現不同地區的疊前地震子波提取.

2.2 柯東地區實際地震資料處理及結果分析

為了驗證基于生成對抗網絡的疊前地震子波提取方法在實際地震資料子波提取中的有效性及優越性，采用了柯東地區疊前共中心點地震炮記錄進行子波提取實驗，并采用稀疏反褶積方法對疊前地震記錄進行了反褶積處理，從圖9中可以看出，基于生成對抗網絡的疊前地震子波提取方法反褶積結果與基于VMD的疊前地震子波提取方法的結果相比，地震記錄同相軸更加清晰，疊前地震剖面的分辨率更高.

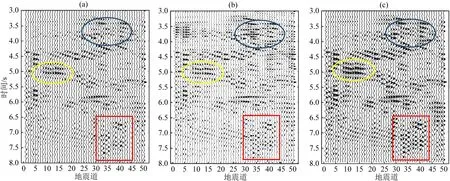
圖9 疊前地震記錄反褶積結果對比圖(a) 柯東地區疊前共中心點炮記錄(第1～50道); (b) 采用VMD算法提取地震子波后的反褶積結果； (c) 本文方法的反褶積結果.Fig.9 Comparison of deconvolution results of pre-stack seismic records(a) Pre-stack CMP record in Kedong area (track 1～50)； (b) Deconvolution results after seismic wavelet extracting by VMD algorithm； (c) Deconvolution results by the method in this paper.

3 結論

本文提出采用一種基于生成對抗網絡算法的疊前地震子波提取技術，針對塔里木柯東地區的地質構造及噪聲特性，利用基于有限差分的正演方法建立柯東地區合成疊前地震記錄樣本集利用生成對抗網絡對樣本集進行學習訓練，實現對塔里木柯東地區疊前地震子波的準確提取.相比于傳統地震子波提取方法，基于生成對抗網絡的疊前地震子波提取算法速度更快，合成數據和實際地震資料的數值實驗都表明了方法的有效性及準確性.本文在提取過程中尚未考慮子波的時空變特性，下一步將研究時空域疊前地震子波的準確提取.