基于應變率變化的爆破塊度預測模型及應用

翟小鵬，楊 軍，陳占揚，湯 宇，陳忠輝

(1.北京理工大學爆炸科學與技術國家重點實驗室，北京 100081； 2.北京奧信化工科技發展有限責任公司，北京 100040)

巖石在高速沖擊、爆炸等動態載荷的作用下會碎成很多小塊，該過程是一個復雜的物理過程，塊度尺寸不僅與巖石的性質有關，與載荷的加載方式也有很大關系。

在爆破實踐活動中，影響塊度的因素有很多，主要包括爆破參數和巖體性質兩方面。已有大量的學者對爆破破巖機理和工程應用開展了相關研究，提出了很多的塊度預測模型。根據模型的假設條件和理論基礎，可以分為應力波模型、經驗函數模型、能量模型、分形理論模型和神經網絡模型五類。應力波模型是根據應力波在巖體中的傳播規律，以不同的破巖理論為依據對爆破過程進行分析，計算單元應力狀態，并將其應用于爆破塊度預測。應力波模型主要包括：HARRIES模型[1]、BMMC模型[2]、BCM模型[3]、能流分布模型[4]，該類模型的特點是能夠對爆破過程進行定量的計算，但普遍將巖體假設為均質材料，不考慮巖體構造的影響，計算結果與實際爆破結果往往存在較大的差異。經驗函數模型是以函數形式表示爆破塊度的總體分布情況，可以全面了解產物的破碎程度。常見的分布函數模型有：KUZ-RAM模型[5]、BOND-RAM模型[6]、別茲馬特類赫模型[7]，該類模型建立了爆破參數與爆破塊度的關系，計算簡便、快捷，但計算精度普遍較低。能量理論模型以破碎功理論為基礎，提出爆破塊度預測的經驗公式。能量理論模型主要有： GAMA模型[8]、JUST模型[9]等，該類模型需要進行大量大爆破試驗來確定相關參數，而且計算精度較低。分形理論模型認為巖石內部的斷裂形狀具有自相似性，局部裂紋的擴展即可得到巖體整體的破碎形態，建立了分形維與爆破塊度的關系[10-11]，但該方法還不成熟，在爆破領域使用較少。神經網絡模型將影響塊度的因素進行整合簡化，通過機器學習來獲得塊度分布相關參數[12-13]，該類模型塊度預測準確，但由于神經元網絡基于風險最小化原則，所以容易出現訓練速度慢、過擬合等理論上難以解決的問題[14]。同時，神經網絡模型的應用需要大量的數據樣本作為支撐，也影響了它的使用和推廣。

在爆破塊度預測方面，已經有很多包含了臺階爆破參數的經驗和半經驗模型，但大多數參數均為爆破參數，即使考慮到巖體性質也只是給出巖石試件的力學參數，并不能全面反映巖體的性質。爆破塊度主要是由巖體內部的構造裂隙擴張產生的，巖體構造才是控制爆破塊度的主要因素[11]。因此，建立一種能夠反映巖體整體性質的塊度預測模型，對礦山生產有著重要意義。

1 理論計算

1.1 應變率-塊度分布模型

目前學界普遍認為，巖石的動態斷裂是材料內部微裂紋的擴張和傳播的造成的。Grady等[15-16]通過對巖石的動態破碎過程進行了研究，認為巖石破碎后的尺寸與應變率存在指數關系，并得出以下計算公式：

(1)

Grady等[15-16]給出的斷裂模型指示巖石的斷裂的塊度尺寸與應變率相關，且與應變率的-2/3次方成正比。即巖石在高應變率加載的情況下，碎裂的塊度與應變率存在指數關系。相關學者也進行了大量的研究，結果表明巖石的斷裂尺寸和應變率存在指數關系[17-18]。因此，巖石爆破破碎的塊度可以參考此結論建立模型。

在爆破作業中，爆區塊度由炮孔近區至遠區依次增大，而應變率是依次減小。因此，對于露天臺階爆破塊度分布規律，可以建立一種基于應變率變化的塊度分布的模型，函數表達式為

(2)

通過這種方式可以將塊度預測模型推廣到更廣泛的工況當中，來解決實際工程中的塊度預測問題。p、q為該塊度預測模型中的核心參數，在不同的工程條件下，這兩個參數只對特定的爆破對象具有一定的精度。因此，需要根據不同的工況來確定參數。

1.2 炮孔近區應變率變化規律

一般而言，炮孔近區指的是30～50倍孔徑范圍內的巖體[19]。由于爆炸作用高強度沖擊波及高溫、高壓氣體的作用，在炮孔近區很難測得應變率的變化規律。因此，利用柱面波協調方程，引入柱坐標下徑向應變率與振動速度參數的表達式[20]：

(3)

由式(3)可知，若已知爆炸作用下炮孔近區各點峰值速度的徑向衰減規律，便可求得該點應變率的值。依據波動理論，柱坐標系下應力波在介質中的傳播同時滿足質量及動量方程：

ρ0D=ρ1(D-v1)

(4)

P1=ρ0Dv1

(5)

式中：D為沖擊波波速，m/s；P1為擾動巖體內部的壓力值，kPa；ρ0、ρ1分別為擾動前后巖體密度，kg/m3；v1為擾動巖體的質點速度，m/s。

由Hugoniot方程可知，巖石中沖擊波傳播速度與質點的振動速度具有如下關系[21]：

D=a+bv

(6)

式中：a、b為與巖石力學性質有關的參數；a與聲波在巖石內傳播的速度基本相同，m/s；b的取值范圍為1.0～1.5。

由于露天臺階爆破一般情況下為耦合裝藥，因此，爆生氣體只有等熵膨脹狀態，炮孔壁的壓力值為[22]

(7)

式中：pr0為炮孔壁的壓力峰值；ρe為炸藥密度；D為炸藥爆速；k為絕熱指數，一般取k=3；n為沖擊波碰撞壓力增大倍數，n=8～11，取n=8。

聯立式(4)～式(7)可得炮孔壁初始質點最大振動速度：

(8)

式中：vr0為炮孔壁質點最大振動速度；ρ0為擾動前巖體密度；其余參數同前。

對于沖擊波及應力波的傳播與衰減問題，通常采用指數函數來表示[23]：

(9)

(10)

式中：σr為柱坐標系下距離炮孔中心r處的壓力峰值；νr為距離炮孔中心為r處的質點速度；α為沖擊波或應力波衰減指數，α的取值為1.5～3.0；r0為炮孔半徑；r為質點距離炮孔中心的距離。

由式(10)，質點振動速度隨徑向距離的增大呈指數型衰減，對式(10)求偏倒數近似求得柱坐標系下炮孔近區巖體應變率的計算公式：

(11)

由式(11)可以看出，炮孔近區的應變率隨距離的增加呈指數衰減，衰減速率不僅與炸藥的特性有關，與巖體性質也有很大的關系。臺階爆破過程中，近區巖體的徑向應變率值大于環向應變率，所以采用較大的徑向應變率表征質點的應變率。該公式能夠給出炮孔近區不同范圍內應變率的解析解，這對于解決炮孔附近塊體破碎的塊度預測問題有著重要意義。

1.3 爆孔近區塊度分布規律

在露天臺階爆破過程中，影響爆破塊度的因素有很多，其中最重要的就是臺階爆破參數與巖體性質。爆破設計的各項參數容易獲得，而礦山巖體的地質條件變化頗大，巖體內部存在大量性質不同、產狀各異的裂隙，不僅影響著巖體力學性質，也影響著巖體破壞形式。相關研究表明，對于節理發育的巖體，巖體構造才是影響爆破塊度的主控因素。即在合理的爆破參數下，巖體的性質對塊度的最終分布起著決定性的作用。

在工程實踐過程中，通常是爆破后通過篩分或圖像分析的方式對巖塊大小進行統計分析，得出塊度分布規律，進而評價爆破效果的優劣。在爆破施工前，一般是通過經驗公式對塊度進行預測，該方法簡潔高效，但存在很大誤差。相同的爆破參數，不同的巖石的爆破效果千差萬別。因此，建立一種與巖體性質相關的塊度預測模型，對于快速高效地對露天臺階爆破進行預測，指導礦山實際生產有著重要意義。

建立炮孔近區的塊度分布模型，實現對爆破近區的塊度預測。將式(11)代入式(1)得出炮孔近區塊度分布函數：

y=

(12)

式中：y為炮孔半徑r處塊度的大小；p、q為相關系數，其取值與巖體結構特性相關(包括各種結構面、弱面的分布情況及弱面的充填物性質)。其余參數同前。

式(12)中除p、q外，所有參數都容易獲得。而p、q的取值往往只對特定的對象具有較高的精度，并不具有廣泛的適用性，在不同的工程條件下需要單獨考慮。在爆破參數固定的情況下，影響p、q取值的最主要因素便是巖體組成、結構特性。因此，對于指定礦山，只要針對某種巖體提取爆后塊度信息，即可很方便地獲取p、q，從而對該種巖體的爆后塊度進行預測。

2 工程應用

湖山鈾礦位于納米比亞Erongo地區的納米布沙漠，西部毗鄰大西洋，礦區距離科普斯瓦蒙德鎮約60 km，與ROSSING鈾礦相鄰。湖山鈾礦是世界開采規模最大的鈾礦，年開采剝離量1.4億t，年處理礦石1 500萬t，設計年產量6 800 t U3O8，礦區總體儲量可以滿足20臺百萬千瓦級核電機組近40年的天然鈾需求，主要為中廣核集團在國內運營的核電站提供鈾原料。

地質工程師嘗試對當地已有的地層單元進行詳細劃分，建立以巖性為標識的細分地質模型，但由于巖性組合復雜多變，未能實現這一目標。現場的地質情況很復雜，每個地層都不同的層序，各地層之間接觸關系紛雜，部分地區褶皺發育，覆蓋層最大厚度大15 m。湖山鈾礦地層及巖性如表1所示。

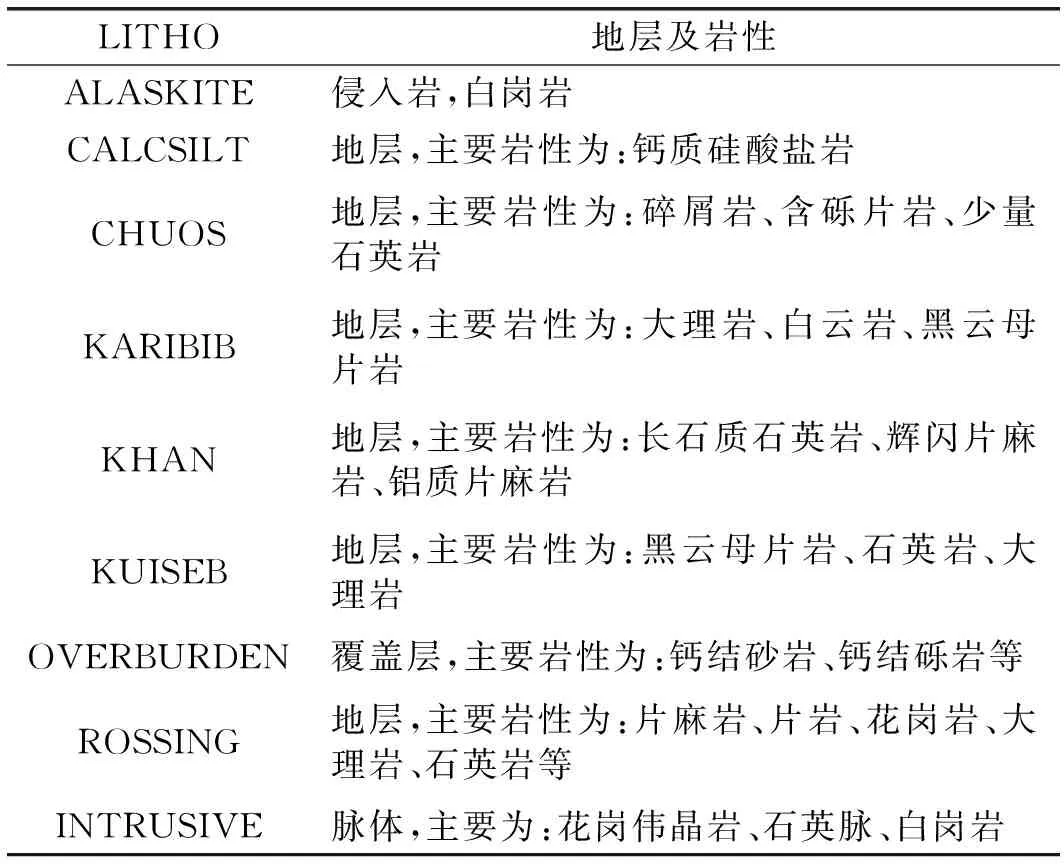
表1 湖山礦地層及巖性

湖山鈾礦共包含CALCSILT、CHUOS、KARIBIB、KHAN、KUISEB、ROSSING 6個地層，侵入巖為白崗巖，脈體為花崗偉晶巖、白崗巖和石英巖。

以2號坑1期的2B31D015臺階為例，對露天臺階爆破塊度預測方法進行驗證。臺階位2號坑1期，坡底標高為15 m，臺階長度83 m，寬度為35 m，共有炮孔126個。2B31D015臺階巖性主要為白崗巖。2B31D015臺階的爆破設計參數、白崗巖及炸藥參數分別如表2、表3所示。將相關參數代入式(12)，得：

(13)

式中：y為巖塊尺寸，m；r為距離炮孔中心距離，m；p、q為與巖體結構相關的參數。

表2 2B31D015爆破設計參數

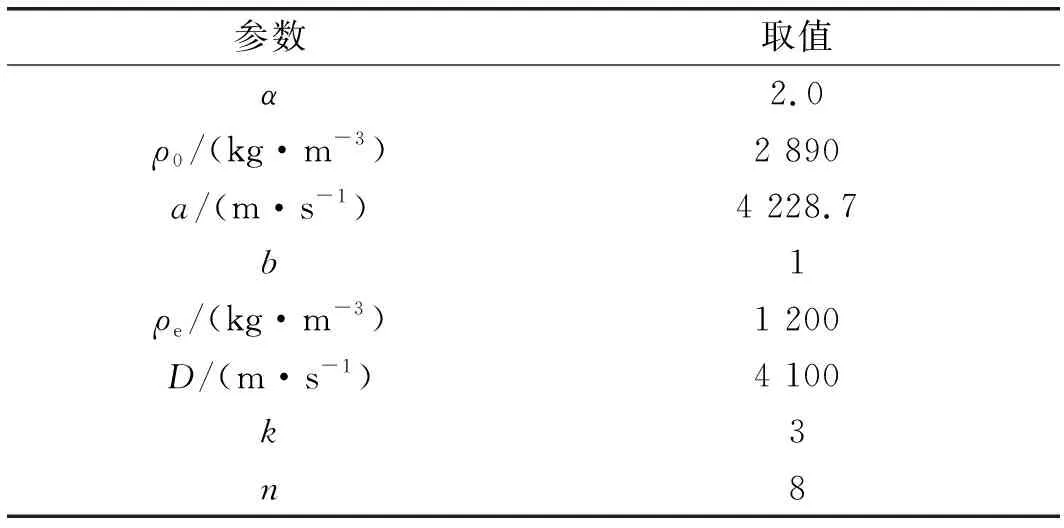
表3 白崗巖及炸藥參數

單孔負擔體積V=a(孔距)×b(排距)×H(臺階高度)，2B31D015臺階a=5.4，b=4.3；根據單孔負擔體積計算不同尺寸巖塊所占累積比例：

(14)

式中：F為塊度累積百分比，x為巖塊尺寸，m。

2號坑1期的2B31D009、2B31D010、2B31D012、2B31D013、2B31D014臺階均為白崗巖，而且爆破設計參數相同。對上述5個爆區的爆破后的不同階段的開挖面設置參照物，并進行圖像拍攝。最后利用Split-desktop 4.0軟件對爆破的塊度進行分析，得出各臺階的塊度分布曲線，利用數據回歸的方式得出式(14)中參數p=0.98，q=—1.334 8，將p、q代入式(14)得出在白崗巖的塊度分布特征函數：

F=1.025x0.499,x≤0.952 5

(15)

式(15)即為白崗巖在表2、表3的爆破參數下的塊度預測公式。當爆破參數發生改變時，將調整后的參數代入式(12)中重新計算公式，即可得出新的塊度預測公式。將p、q的值代入到式(12)中即可得到炮孔近區塊度分布的規律。即可得出在表2、表3的爆破參數下白崗巖炮孔近區的塊度分布公式：

y=0.172r4.004 4,x≤30r0

(16)

臺階實測孔位坐標如圖1所示，虛線標記處為一自由面，其他三面夾制。爆區采用乳化炸藥現場混裝車進行裝藥，孔內管、地表管均為ORICA公司生產，起爆彈為SASOL公司生產的Pentolite型起爆彈。地表管孔間延時42 ms，排間延時100 ms。起爆網路如圖2所示。

圖1 2B31D015臺階實測孔位坐標Fig.1 Hole coordinates ofbench 2B31D015

圖2 2B31D015臺階爆破網路Fig.2 Firing circuit of bench 2B31D015

2B31D015臺階爆破后，以直徑25 cm的籃球作為標記物，對不同時間的8個開挖面拍攝。利用Split-desktop 4.0對圖像進行塊度分析(見圖3)，其中藍色表示巖塊之間界線，紅色表示巖粉，淡綠色為不分析區域(巖墻、地面等)。

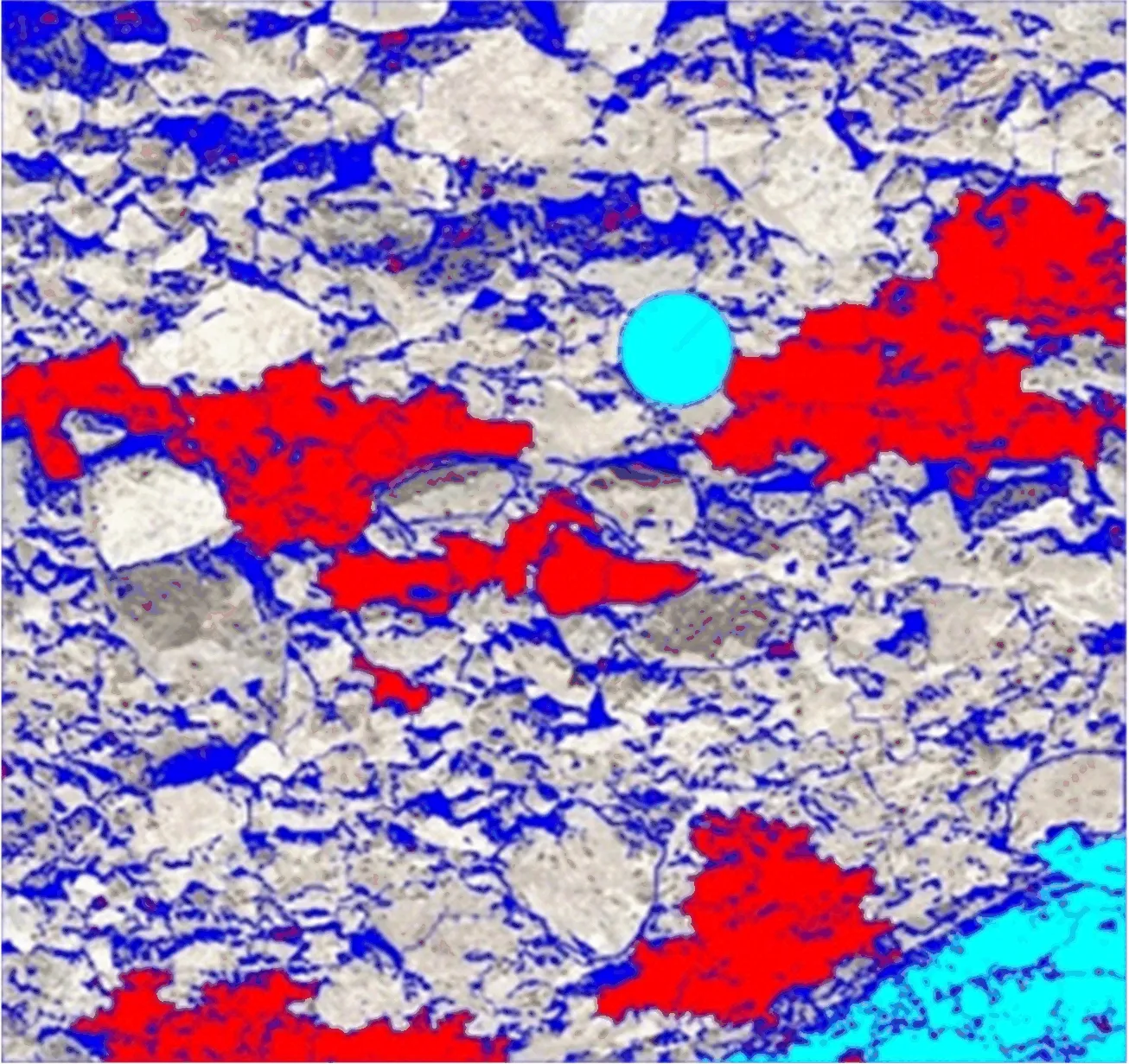
圖3 塊度分析Fig.3 Block analysis

對塊度分析結果進行統計分析，最終得出爆堆的塊度整體分布數據和曲線。2B31D015臺階的塊度分布如圖4所示。

圖4 2B31D015臺階的塊度分布Fig.4 Fragmentation distribution curve of bench 2B31D015

利用式(15)白崗巖的塊度預測公式繪制塊度分布曲線，與現場統計的塊度曲線進行對比，結果如圖5所示。

圖5 2B31D015臺階實測與預測塊度對比Fig.5 Comparison of measured and predicted Fragmentation size of bench 2B31D015

由圖5可以看出，預測塊度曲線與實測塊度曲線趨勢基本一致，能夠反映爆破塊度的分布特征。將塊度預測值與實測值進行對比，分析預測誤差(見表4)。結合圖5與表4可知，F30及以下預測誤差偏大；F40～F60有最高的預測精度，平均誤差為8.1%；F70～F100也有較高的精度，平均誤差為16.17%，預測結果與實測結果基本一致。總體而言，預測誤差在工程可接受的范圍內。

表4 塊度預測誤差分析

3 結論

1) 對現有的塊度預測方法，根據模型的理論基礎和假設條件，可以分為應力波模型、經驗函數模型、能量模型、分形理論模型和神經網絡模型。并對其優缺點進行了評述，認為巖體構造是控制爆破塊度的主要因素。

2) 從理論上分析了炮孔近區應變率的變化規律，結合炮孔近區塊度的分布函數，推導了應變率-塊度的分布模型。對不同巖性的爆區，通過數據回歸的方式獲得了塊度分布函數的相關參數。該函數考慮了巖體結構對爆破塊度的影響，不僅能夠對塊度的整體分布進行預測，同時也能夠定量計算炮孔近區不同范圍內巖塊的尺寸。

3) 針對現場爆破效果，采用對爆堆的不同開挖面進行拍照和圖像分析的手段，得到實際的塊度分布曲線。通過驗證分析得知，基于應變率變化的塊度預測模型的F50～F80的平均誤差為12.5%，能夠較為準確地預測爆破塊度。