求解絕對值方程的捕魚算法

陳建榮　陳建華

摘? 要： 提出一種求解絕對值方程的捕魚算法。算法首先將絕對值問題轉化為一個最小化問題，然后使用三種搜索模式對目標函數(shù)進行尋優(yōu)。數(shù)值實驗結果表明，與粒子群算法和人群搜索算法以及他們的改進算法相比，所提算法不僅獲得了穩(wěn)定的求解結果，而且在最小值、最大值、平均值和方差等指標上均明顯優(yōu)于其他對比算法。

關鍵詞： 絕對值方程; 群智能算法; 捕魚算法; 優(yōu)化

中圖分類號：TP183? ? ? ? ? 文獻標識碼：A 文章編號：1006-8228（2022）02-72-04

Fishing algorithm for solving absolute value equations

Chen Jianrong1， Chen Jianhua2

（1. School of Public Health and Management， Youjiang Medical University for Nationalities， Baise， Guangxi 533000， China;

2. You Jiang District medical security service center）

Abstract： A fishing algorithm for solving absolute value equations is proposed. The algorithm transforms the absolute value problem into a minimization problem， and then optimizes the objective function by using three search modes. Numerical experimental results show that compared with particle swarm optimization algorithm， crowd search algorithm and their improved algorithms， the proposed algorithm not only obtains stable solution results， but also is obviously superior to other comparison algorithms in minimum， maximum， average and variance.

Key words： absolute value equations; swarm intelligence algorithm; fishing algorithm; optimization

0 引言

絕對值方程等價于一個不可微的NP難問題，其最初研究主要來源于區(qū)間線性方程和線性互補問題[1-2]。目前，對絕對值方程的研究主要在理論、算法和應用幾個方面，取得了一定成果[3-9]。Rohn[3]和Mangasarian[4]首先對絕對值方程進行了引領性的研究，并給出了包括解的存在性與數(shù)量的相關理論。Yu[5]和Chen[6]分別通過改進的多元譜梯度算法和無逆動力系統(tǒng)對絕對值方程來求解。封[7-8]等人則通過使用粒子群和人群搜索算法來獲得絕對值方程問題的解。雍[9]則提出了一種五階牛頓迭代法求解絕對值方程。

群智能算法是一種通過模擬自然界中動物（或昆蟲等）的群體行為而提出的一類隨機搜索方法，屬于一種新興的演化計算技術，前文提及的粒子群和人群搜索算法都屬于這一類算法。由于群智能算法具有明顯的并行性特征，魯棒性也較好，因而得到了國內外學者的普遍關注和研究[10-13]。陳[13]等人通過觀察和模擬漁夫在江面上捕魚的行為習慣而提出了采用捕魚策略的優(yōu)化算法（Fishing Strategy Optimization Algorithm），即捕魚算法（Fishing Algorithm）。該算法在求解高爐料面?zhèn)鞲衅鞑贾肹14]、TSP問題[15]和約束優(yōu)化[16]等問題中表現(xiàn)出較好的性能。

1 問題描述與轉化

本文考慮的絕對值方程（Absolute Value Equation，AVE）具有如下的形式[3]：

Ax-|x|=b]?⑴

其中，A∈R，x，b∈R，|x|表示對x中的每一個分量取絕對值。其廣義形式是[4]?Ax+B |x|=b。

引理1[1] 如果[A]的所有奇異值均大于1，那么對于?b∈R，⑴的解存在且惟一;如果A滿足||A||≤1，那么對于?b∈R，⑴的解存在且惟一。

引理2[1] 如果b<0，且||A||<γ/2，γ=min|b|/max|b|），那么⑴有完全不同的2個解，且每個解都沒有零分量，符號也不同。

為求得絕對值方程⑴的解，首先將其轉化為如下的最小化問題[7]：

2 捕魚算法簡介[13]

作為一種群智能優(yōu)化算法，捕魚算法的基本假設包括如下七個方面：①漁夫的行為對水中魚的密度無影響;②漁夫不知道水中魚的分布情況;③漁夫往魚密度大的方向前進以便能捕到更多的魚;④漁夫會停留在魚的密度比四周高的位置捕魚;⑤漁夫使用網(wǎng)眼更小的漁網(wǎng)以便將魚一網(wǎng)打盡;⑥若當前位置沒有魚或者魚比較少，那么漁夫會嘗試到其他地方捕魚;⑦漁夫之間避免碰撞。

算法主要通過移動搜索、收縮搜索和隨機搜索三種搜索模式對漁夫的行為習慣進行模擬。在開始時，首先在定義域范圍內對漁夫個體的位置等參數(shù)進行初始化;然后各漁夫根據(jù)自己所處的狀態(tài)來選擇不同的搜索模式進行搜索和狀態(tài)更新;最后，在漁夫們的共同努力下找到問題的最優(yōu)解。

3 求解絕對值方程的捕魚算法

3.1 基本參數(shù)

算法設置有公告板，用于記錄迭代過程中漁夫找到的最優(yōu)值[F（xB）]及對應的最優(yōu)解[xB]。此外，需要設置的參數(shù)還包括最大迭代次數(shù)[φ]、漁夫規(guī)模m、步長[λ]、收縮系數(shù)[δ]和閾值[ε]。

3.2 漁夫個體

3.3 目標函數(shù)

結合⑵，得到求解絕對值方程的捕魚算法的目標函數(shù)如下：

⑶ 隨機搜索

對第i個漁夫的位置進行隨機初始化，并還原其步長和閾值，根據(jù)⑶重新構造撒網(wǎng)點集。

3.5 算法流程

算法流程如下。

步驟1：在定義域范圍內隨機初始化m個漁夫的位置;

步驟2：如果算法迭代次數(shù)達到[φ]，則程序停止并將公告板記錄值輸出;

步驟3：根據(jù)漁夫的狀態(tài)選擇執(zhí)行相應的搜索模式;

步驟4：如果找到更優(yōu)值則更新公告板，否則轉步驟2。

4 數(shù)值實驗及分析

4.1 實驗環(huán)境及參數(shù)

實驗使用的計算機軟硬件配置：Intel（R） Core（TM） i7-4790K CPU @ 4.00GHz（睿頻4.8GHz），32GB雙通道DDR3 2400MHz內存，64位Windows 10專業(yè)版操作系統(tǒng)，MATLAB版本為R2020a。

為消除算法參數(shù)、初始值等因素對本文算法的影響，在數(shù)值實驗中采取如下方法：①每次運行時，使用MATLAB中的隨機函數(shù)對漁夫位置進行初始化;②對于每一個算例，本文算法均獨立運行20次;③對于所有的算例，將本文算法的參數(shù)統(tǒng)一設置為：漁夫規(guī)模[m=50]、最大迭代次數(shù)[φ=100]、步長[λ=0.6]、收縮系數(shù)[δ=0.5]和閾值[ε=10]。

4.2 實驗算例及結果

數(shù)值實驗中使用的四個算例[7-8]如下。

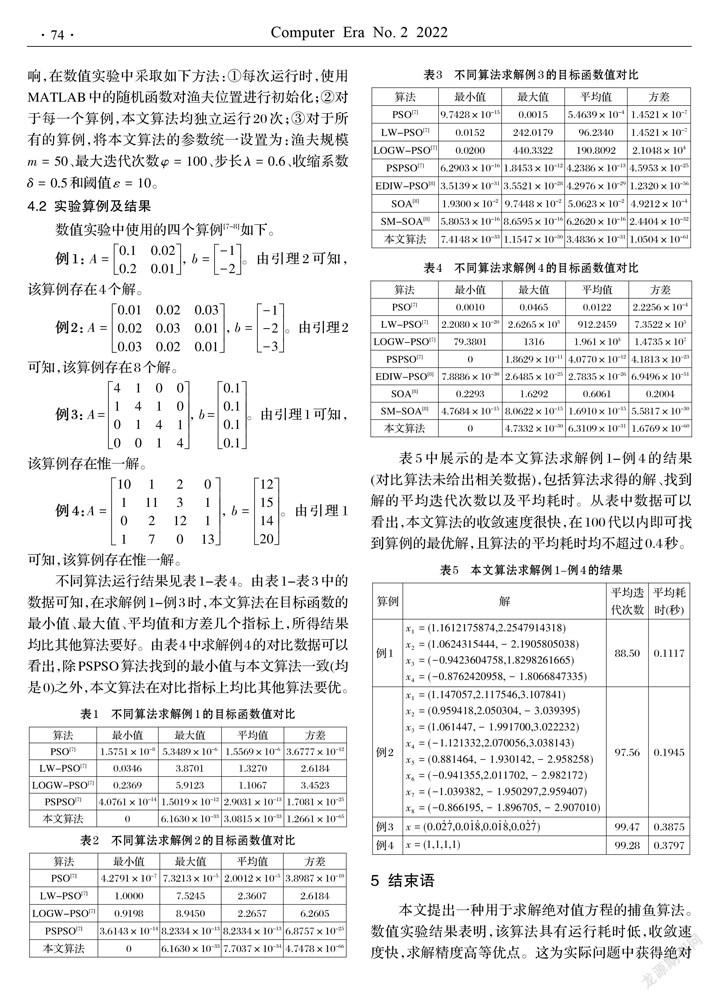
不同算法運行結果見表1-表4。由表1-表3中的數(shù)據(jù)可知，在求解例1-例3時，本文算法在目標函數(shù)的最小值、最大值、平均值和方差幾個指標上，所得結果均比其他算法要好。由表4中求解例4的對比數(shù)據(jù)可以看出，除PSPSO算法找到的最小值與本文算法一致（均是0）之外，本文算法在對比指標上均比其他算法要優(yōu)。

表5中展示的是本文算法求解例1-例4的結果（對比算法未給出相關數(shù)據(jù)），包括算法求得的解、找到解的平均迭代次數(shù)以及平均耗時。從表中數(shù)據(jù)可以看出，本文算法的收斂速度很快，在100代以內即可找到算例的最優(yōu)解，且算法的平均耗時均不超過0.4秒。

5 結束語

本文提出一種用于求解絕對值方程的捕魚算法。數(shù)值實驗結果表明，該算法具有運行耗時低，收斂速度快，求解精度高等優(yōu)點。這為實際問題中獲得絕對值方程的解提供了一種有效的算法。下一步將嘗試對高維的絕對值問題求解，并對算法的性能做更深入的研究與測試，以進一步拓寬其應用范圍。

參考文獻（References）：

[1] Rohn J. Systems of linear interval equtions[J].LinearAlgebra and its Applications，1989，126：39-78

[2] 韓繼業(yè)，修乃華，戚厚鐸.非線性互補理論與算法[M].上海：上海科學技術出版社，2006

[3] Rohn J. A theorem of the alternatives for the equation Ax+B|x|=b[J]. Linear and Multilinear Algebra，2004，52（6）：421-426

[4] Mangasarian O L， Meyer R R. Absolute value equations[J].Linear Algebra and its Applications，2006，419：359-367

[5] Yu Z S， Li L， Yuan Y. A modified multivariate spectral?gradient algorithm for solving absolute value equations[J].Applied Mathematics Letters，2021，121：107461

[6] Chen C R， Yang Y， Yu D M， Han D R. An inverse-free?dynamical system for solving the absolute value equations[J]. Applied Numerical Mathematics，2021，168：170-181

[7] 封京梅，劉三陽.基于模式搜索的粒子群算法求解絕對值方程[J].蘭州大學學報（自然科學版），2017，53（5）：701-705

[8] 封京梅，劉三陽.基于單純形法進行局部優(yōu)化的人群搜索算法求解絕對值方程[J].吉林大學學報（理學版），2019，57（5）：1075-1080

[9] 雍龍泉.一種五階牛頓迭代法求解絕對值方程[J].數(shù)學的實踐與認識，2021，51（7）：261-267

[10] Ntakolia C; Iakovidis D K. A swarm intelligence graph-based pathfinding algorithm （SIGPA） for multi-objective route planning[J]. Computers & Operations Research，2021，133：105358

[11] 陳曉全.基于改進粒子群算法的解耦控制研究與仿真[J].計算機時代，2021（5）：68-72

[12] 張健，范曉武.基于改進蟻群算法的高速公路協(xié)同救援路徑規(guī)劃[J].計算機時代，2021（3）：1-6

[13] 陳建榮，王勇.采用捕魚策略的優(yōu)化方法[J].計算機工程與應用，2009，45（9）：53-56

[14] 苗亮亮，陳先中，侯慶文，等.高爐料面?zhèn)鞲衅鞑贾玫幕煦绮遏~策略[J].儀器儀表學報，2014，35（1）：132-139

[15] 陳建榮，陳建華.求解TSP問題的離散捕魚策略優(yōu)化算法[J].計算機科學，2017，44（S1）：139-140，160

[16] 陳建榮，陳建華.求解約束優(yōu)化問題的自適應精英捕魚算法[J].信息技術，2019，43（4）：91-95