離散雙切換線性正系統的L1增益性能分析

席 敏，龍 飛

(1.貴州大學大數據與信息工程學院，貴州 貴陽 550025；2.貴州理工學院人工智能與電氣工程系，貴州 貴陽 550003)

0 引言

離散時間切換正系統是一類特殊的混雜系統，由多個正子系統和控制子系統間切換次序的切換信號構成。切換信號可分為確定性切換信號和隨機切換信號。正系統是初始條件和輸入非負時，狀態和輸出也為非負的系統。正系統變量非負這一特性，廣泛運用在生物學、經濟學、網絡通信、人口統計學、實際生產活動等系統建模中。例如，計算機網絡協議傳輸控制系統、自動化切換電路系統[1-2]等。

對切換正系統進行穩定性分析時，不僅要保證整個系統穩定，還需考慮系統的正性。這增加了研究切換正系統的復雜度和難度。關于切換系統的穩定性的理論研究，形成了以Lyapunov函數、駐留時間(dwell-time,DT)、平均駐留時間(average dwell-time,ADT)、持續駐留時間(persistent dwell-time,PDT)和Co-positive Lyapunov函數等為主的分析方法。現有研究結果表明，相比傳統線性Lapunov函數法，Co-positive Lyapunov函數法存在更低的保守性[3]。

切換正系統在運行時，不可避免地含有隨機故障或不可控因素引起的系統動態參數變化。隨機切換系統——馬爾可夫跳變線性系統(Markov jump linear system,MJLS)常用來描述此類系統。MJLS是由隨機切換信號(即Markov鏈)協調系統模態間切換的隨機切換系統。對于MJLS的穩定性研究結論有均方穩定(mean-square,MS)、幾乎處處穩定(exponential almost-sure stability,EAS)等。

由于混雜系統的復雜性，通過對切換系統的結構作變化，可將切換系統分為不同類型。本文中的切換正系統結構是受到確定性切換信號和隨機切換信號的影響的離散時間雙切換線性正系統(discrete-time dual-switched linear positive systems，DDSLPS)。

在DDSLPS中，子系統由多個不同的MJLS構成。每個MJLS子系統服從不同的Markov鏈。第一層切換由確定性切換信號γk控制MJLS子系統間的切換。第二層切換由各MJLS的Markov鏈σk控制系統模態間的切換。在Markov子系統間發生切換時，各Markov系統模態也在同時發生切換。相比一般切換正系統只有一個切換信號來控制系統運行，例如MJLS由Markov鏈控制系統模態間的切換，DDSLPS必須考慮確定性切換信號與隨機切換信號對整個系統的影響，以及系統的正性。因此，DDSLPS的穩定性分析和鎮定分析比普通切換系統更加復雜。

對于離散時間切換系統而言，其采樣周期受到時滯的影響。時滯可以是系統中控制器的計算延遲，也可以是控制器和監控器的通信延遲等。這些未知的、時變的、有界的時滯，稱為系統中存在的指數參數不確定性。有學者在文獻[4]中提出了含有指數不確定性的連續時間線性系統的魯棒鎮定問題,將指數不確定性轉換為一個服從加性模有界不確定性的混雜多面體模型。受到此方法的影響，本文將含有指數不確定的DDSLPS轉換為模有界不確定性的系統進行研究。

系統性能不僅受到內部參數改變和時滯帶來的影響，也容易受到外部擾動的影響。為了衡量切換正系統的抗干擾能力，通常用L1增益性能來評估系統干擾抑制水平性能。L1增益系數越小,系統的干擾抑制水平越高。所以對切換正系統的抗干擾性能分析引起了廣泛的關注。文獻[5]研究了切換正系統L1增益性能分析對實際生產系統中的應用，利用Co-positive Lyapunov函數方法,研究了在駐留時間限制下存在時延的離散時間切換正系統的指數穩定性以及L1增益性能，并得到時延對系統L1增益性能的影響。文獻[6]利用線性編程(linear programming,LP)對離散時間正MJLS進行L1增益分析并進行正濾波器設計。利用線性Lyapunov函數構建一個“等價”的確定離散時間線性系統，給出的充分條件能保證系統隨機穩定并有L1增益性能。

本文在以上研究的基礎上，將切換正系統以及離散時間正MJLS對L1增益性能的研究方法應用到DDSLPS中。針對存在指數不確定性的DDSLPS,通過結合Co-positive Lyapunov能量衰減函數、MJLS的暫態分析、PDT等主要理論方法,證明DDSLPS在擾動為零時魯棒-幾乎處處穩定(Ronust-exponential almost-sure stability,Ronust-EAS),并將此證明方法推廣應用于系統L1增益性能分析中。仿真分析充分驗證了結論的正確性。

1 問題描述

本文考慮如下的DDSLPS：

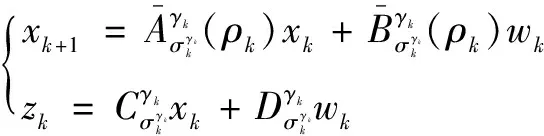
(1)

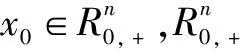
定義1 系統(1)對于所有的x0≥0、wk≥0;對于k∈N,都有x0≥0、zk≥0。

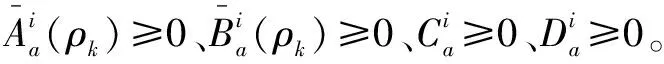
注1 為了便于穩定性分析,將利用指數不確定性的相關引理，把具有指數不確定性的雙切換離散時間線性系統表示為具有附加范數有界不確定性的雙切換離散時間線性多面體系統。

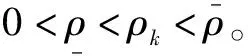
L(ρ)=L0+L1ρ+L2ρ2+…+Lhρh

(2)

所以能找到一個具有(h+1)個頂點的凸組合L(ρ),使得：

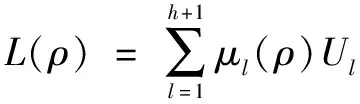
(3)

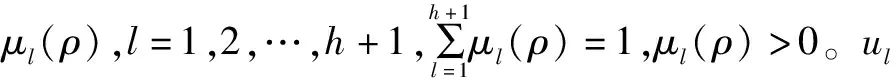
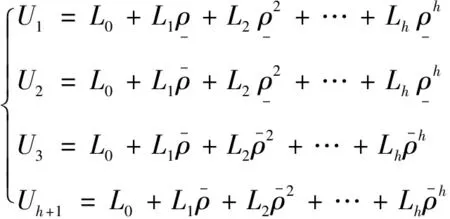
(4)

不確定參數ρ和μl(ρ)的關系如下：

(5)

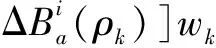
(6)

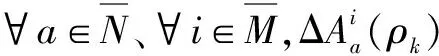
式中：sup表示最小上確界。

注2 綜上可知,具有指數不確定性的雙切換離散時間線性系統已經表示為具有附加范數有界不確定性的雙切換離散時間線性多面體系統,如式(6)所示。系統模型(1)中同時包括了具有多項式的不確定性的雙切換離散時間線性系統和具有范數有界不確定性的雙切換離散時間線性系統。因此,系統(1)可以用于對具有復雜切換特性的系統建模。

注3 為了研究確定性切換系統的穩定性，接下來將闡述持續駐留時間PDT 方法。

定義2[9]考慮切換時刻k0,k1,...,kn。其中,k0=0。假如存在無數個長度大于τ的不相交區間,且具有該性質的連續區間被一個不大于T的時間間隔分割,則常數τ被稱為PDT、T被稱為持續周期。

注4 PDT由切換規則相同的階段構成。每個階段均包括τ和T這兩部分。在τ部分中,只有一個任意的子系統激活并且作用時間至少為τ。在T部分中,有多個子系統激活。每個子系統的作用時間小于τ且所有子系統的激活總時間小于T。

DDSLPS結構如圖1所示。

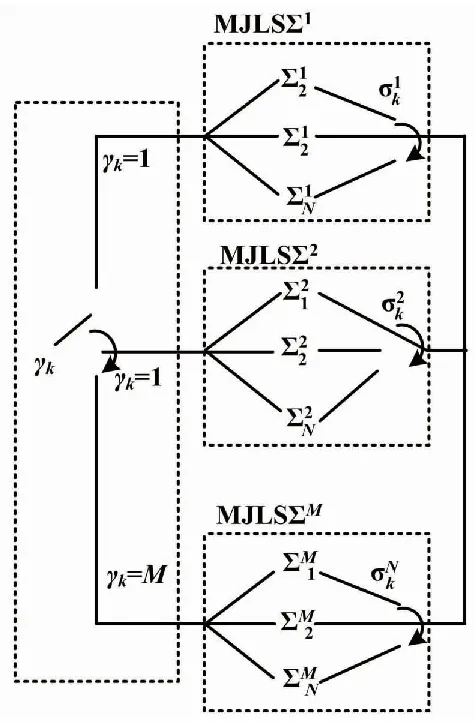
圖1 DDSLPS結構圖

DDSLPS的切換序列如圖2所示。

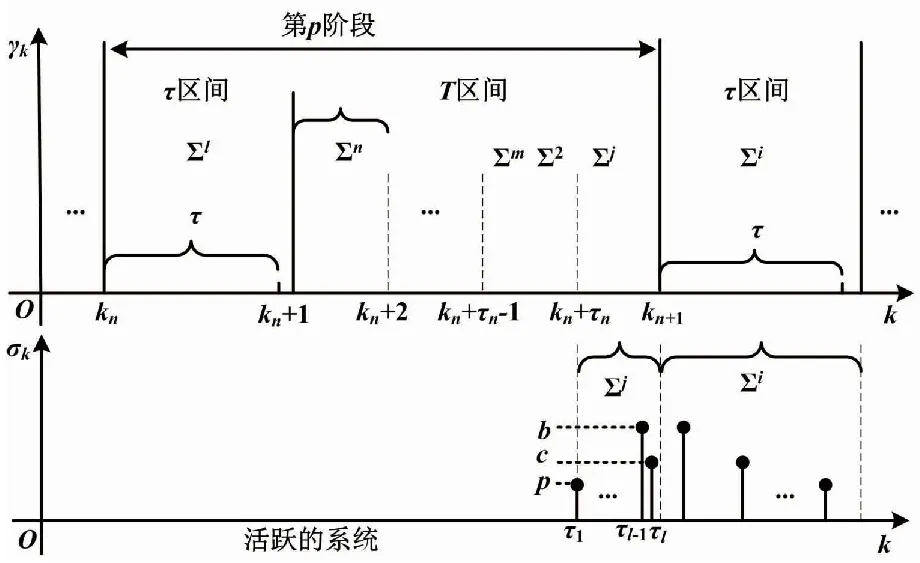
圖2 DDSLPS PDT切換序列

{kn,kn+1,…,kn+τn-1}表示確定性切換信號γk在區間[kn,kn+1)的切換時刻。{τ1,τ2,…,τl}表示隨機切換信號σk在[τ1,τl)的切換時刻。(kn+1)表示第p個階段中時刻kn的下一個切換時刻。kn+1表示第(p+1)個階段的切入時刻。

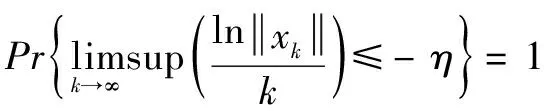
(7)

等價于：

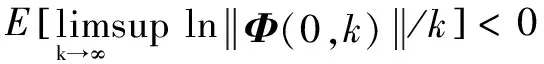
(8)

式中：Φ(0,k)為系統(1)的隨機轉移矩陣。

則在初始概率分布F=[f1,f2…fN]已知時，有以下等式成立：

(9)

(10)

定義4 當常數x>0, 若系統(1)滿足以下兩個條件。

①任意初始條件下,當沒有外部擾動的時候,系統是魯棒EAS穩定的。

②在零初始條件下,對于所有非零干擾wk都滿足所有的可容許不確定性下,有：

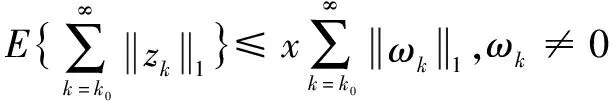
(11)

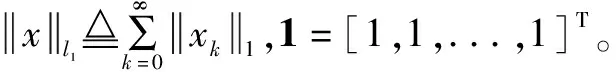
注5 對于DDSLPS而言，由于數量之和對于正系統更可取,使用向量的1范數定義的L1增益更適合于評估性能。x為外部擾動抑制度。x越小，表明系統抵御外界干擾的能力越強。

2 主要結果

2.1 Robust-EAS穩定性

當系統中擾動輸入為零時，系統(1)可以表示為:

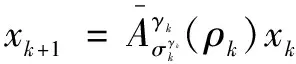
(12)

接下來，給出系統(12)Robust-EAS穩定的充分條件。

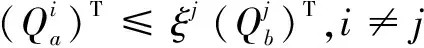
(13)

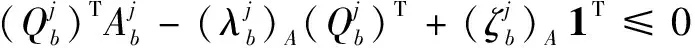
(14)

(15)

(16)

此處：

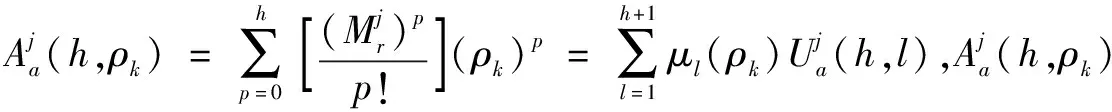
(17)

(18)

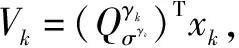
(19)

(20)

在區間[τl,kn+1)上，只有隨機切換系統b模態在作用。由條件式(14)、條件(15)以及重復步驟(17)、步驟(18)，可以得到:

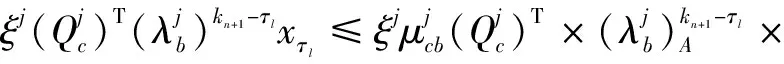
(21)

從條件(9)、條件(10)可以得到:

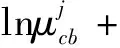
由αj、βj的等式可以得到：

E{lnVkn+1}=βj+αjΔk+E{lnVτ1}

(22)

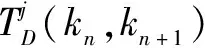
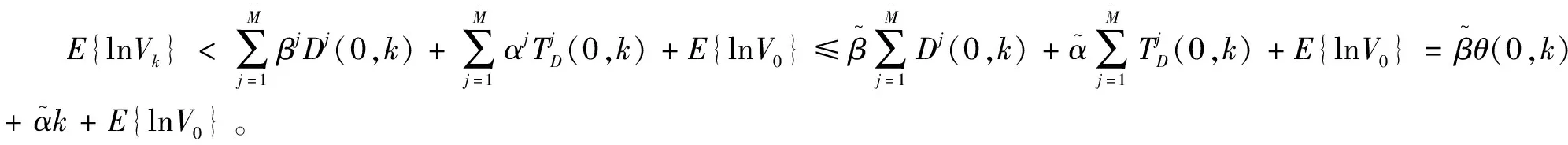
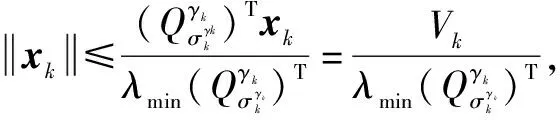
由此，即可證明系統(1)在wk=0 是魯棒EAS穩定的。

2.2 L1增益性能

(23)

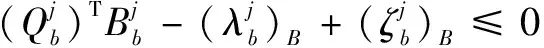
(24)

(25)

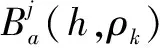
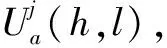
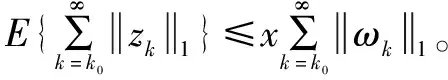
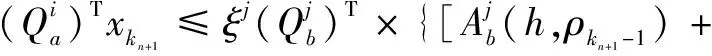
(26)

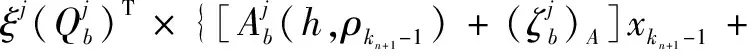
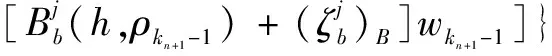
(27)

由條件(14)、條件(15)、條件(24)，得出:

(28)

由式(28)可以得到：

(29)

接下來，按照之前證明wk=0 的步驟，可以得到系統在wk≠0 系統(1)E{Vk}<0。令：

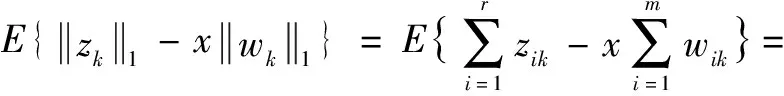
(30)

由式(30)以及條件(23)、條件(25)，可得：

(31)

證明出DDSLPS具有L1增益性能。

3 數值仿真

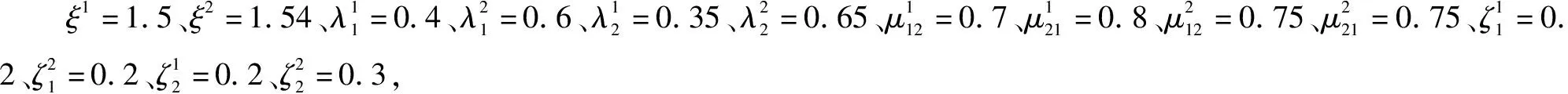
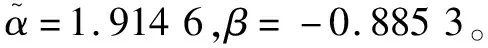
根據條件(18)，系統(1)要保證魯棒EAS穩定，那么PDT的限制為T<0.860 1τ-1.86。選取T=12、τ=22，并選擇以下的PDT限制的周期確定切換信號γk。

式中：n=0,1,2,…；M為確定性切換信號的周期，M=35。

確定性切換信號γk如圖3所示。圖3中：1階段的M為0；2階段的M為1。

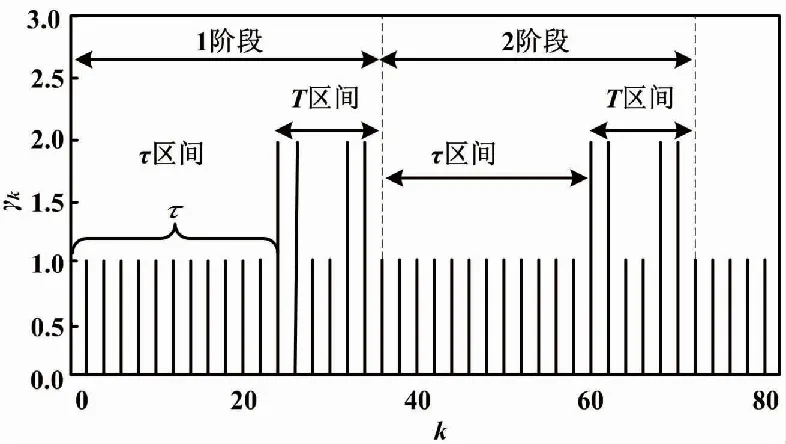
圖3 γk信號示意圖

圖4為系統(1)在w=0、初始條件為x0=[0.6 1]T時的 7次樣本實現。顯然，系統(1)是魯棒EAS穩定的。

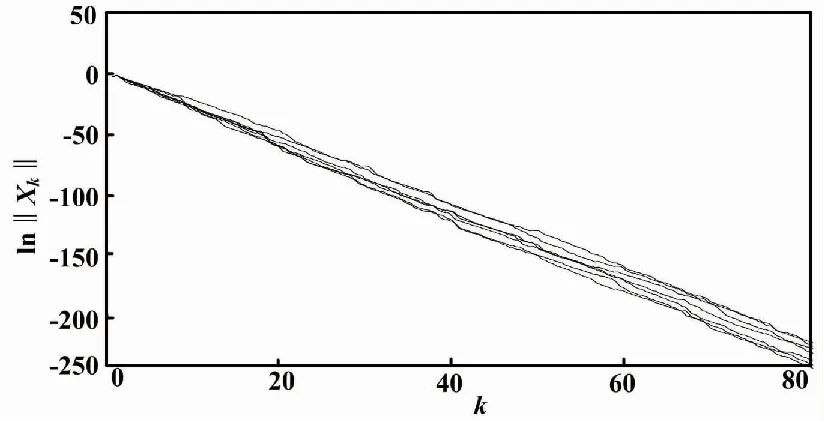
圖的7次樣本實現(w =0)

為考慮擾動抑制性能，外部擾動wk設置為方波信號：

方波信號如圖5所示。

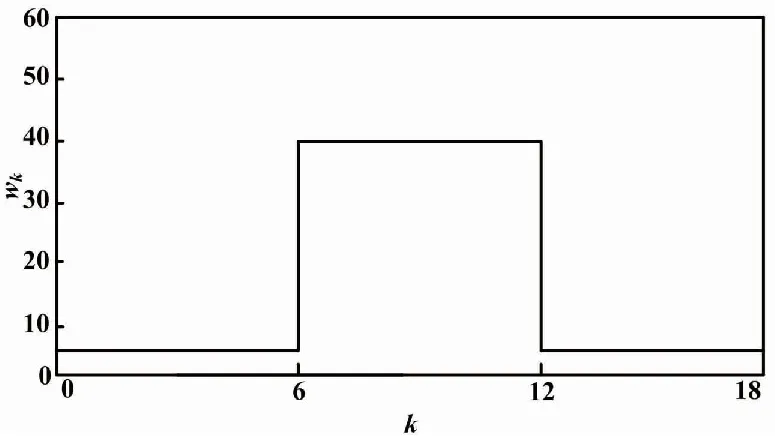
Fig.5 wk信號示意圖

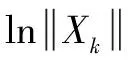
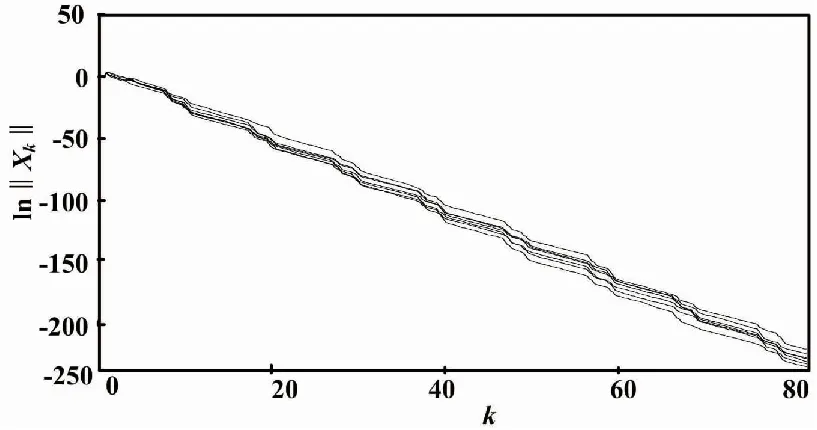
的7次樣本實現(wk ≠0)

4 結論

魯棒穩定以及擾動抑制問題是研究混雜系統穩定性的重要問題。本文對含有指數不確定性的DDSLPS的L1增益性能進行了研究。首先，將指數不確定性轉換為附加范數有界不確定性。然后，利用PDT方法限制確定性切換信號，并基于正系統的理論中的Co-positive Lyapunov能量衰減函數法以及MJLS暫態分析理論，給出了保證DDSLPS Robust-EAS穩定的充分條件，并將此方法推廣得到DDSLPS滿足L1增益性能指標x的充分條件中。最后，得到DDSLPS不僅滿足Robust-EAS且系統具有L1增益性能的充分條件。該條件利用Matlab的LP得出,減少了計算復雜度。仿真算例充分證明了結論的正確性。