元學(xué)習(xí)的不確定性特征構(gòu)建及初步分析

李 艷，郭 劼，范 斌

（1.河北大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，河北保定 071002；2.河北省機(jī)器學(xué)習(xí)與計(jì)算智能重點(diǎn)實(shí)驗(yàn)室（河北大學(xué)），河北保定 071002；3.北京師范大學(xué)珠海校區(qū)應(yīng)用數(shù)學(xué)與交叉科學(xué)研究中心，廣東珠海 519087）

0 引言

特征提取一直是機(jī)器學(xué)習(xí)的重要研究內(nèi)容之一，而元學(xué)習(xí)正是一種充分利用數(shù)據(jù)本身特性的學(xué)習(xí)機(jī)制。元學(xué)習(xí)可被定義為一種應(yīng)用機(jī)器學(xué)習(xí)的方法（元算法）尋求問題的特征（元特征）與算法相對性能測度間的映射，從而形成元知識的學(xué)習(xí)過程。在此學(xué)習(xí)過程中，首先要收集先前學(xué)習(xí)任務(wù)和模型的元數(shù)據(jù)，包括訓(xùn)練模型的精確算法配置、結(jié)果模型評估（例如準(zhǔn)確性和訓(xùn)練時(shí)間）、學(xué)習(xí)的模型參數(shù)（例如神經(jīng)網(wǎng)絡(luò)的訓(xùn)練權(quán)重）以及任務(wù)本身的可測量屬性（也稱為元特征）；然后從這些先前的元數(shù)據(jù)中學(xué)習(xí)、提取和傳遞知識，指導(dǎo)為新任務(wù)尋找最佳模型［1］。

1992 年Aha［2］在算法選擇中引入元學(xué)習(xí)的概念，發(fā)現(xiàn)了問題本身的特征（即元特征）與算法的性能測度之間的關(guān)系。近年來有關(guān)數(shù)據(jù)特征提取的研究［3-4］有了很大進(jìn)展。元學(xué)習(xí)的核心問題之一是元特征的構(gòu)建。2003 年文獻(xiàn)［5］對元特征的提取進(jìn)行了初步的探討，定義了多種數(shù)據(jù)的復(fù)雜度度量，并分析了它們對算法性能的影響；2006 年文獻(xiàn)［6］分別從幾何角度和拓?fù)浣嵌妊芯苛烁呔S空間中點(diǎn)集的特征屬性，得到了不同特征的數(shù)據(jù)集上分類算法的優(yōu)劣；文獻(xiàn)［7］將數(shù)據(jù)復(fù)雜度與學(xué)習(xí)器的表現(xiàn)整合生成綜合數(shù)據(jù)集來判斷學(xué)習(xí)器的學(xué)習(xí)能力。標(biāo)記式學(xué)習(xí)［8-11］試圖通過直接測量一些簡單有效的學(xué)習(xí)算法本身的性能作為模型相關(guān)的元特征來確定特定學(xué)習(xí)問題在所有學(xué)習(xí)問題空間中的位置；文獻(xiàn)［12-15］用數(shù)據(jù)集中的類重疊程度刻畫分類問題的難度。文獻(xiàn)［16-21］的工作通過在人工生成數(shù)據(jù)上進(jìn)行實(shí)驗(yàn)，探討了可能與分類問題復(fù)雜性相關(guān)的數(shù)據(jù)特征，之后有研究分析了數(shù)據(jù)復(fù)雜度對特定分類算法的影響，討論類重疊、特征空間維數(shù)和類密度等一些數(shù)據(jù)特征對不同分類器的影響［22-25］。以上研究中所定義的元特征大部分是數(shù)據(jù)的統(tǒng)計(jì)特征，沒有針對數(shù)據(jù)和模型中的不確定性建立相應(yīng)的元特征。

不確定性建模相關(guān)研究［26-28］表明，數(shù)據(jù)和模型的不確定性對學(xué)習(xí)系統(tǒng)有著顯著影響。文獻(xiàn)［29］研究了根據(jù)問題復(fù)雜度調(diào)整不確定性對分類泛化的影響；文獻(xiàn)［30］研究了不確定性度量對早期時(shí)間序列分類的影響；文獻(xiàn)［31］提出了一種基于鄰域粗糙集的特征選擇方法，使用基于鄰域熵的不確定性度量從基因表達(dá)數(shù)據(jù)進(jìn)行癌癥分類；文獻(xiàn)［32］提出了一種新的基于Jensen-Shannon 散度的直覺模糊集距離度量方法來表示信息的不確定性；文獻(xiàn)［33］對分類任務(wù)的神經(jīng)網(wǎng)絡(luò)預(yù)測中的不確定性進(jìn)行了測量。

本文從不同角度考慮數(shù)據(jù)和模型可能存在的不確定性，提取多種不確定性指標(biāo)作為數(shù)據(jù)的元特征，給出了具體的計(jì)算方法，并在大量的人工數(shù)據(jù)集、真實(shí)數(shù)據(jù)集上利用多個(gè)分類算法的測試結(jié)果分析了這些元特征之間的相關(guān)性，以及它們對學(xué)習(xí)性能的影響。

1 數(shù)據(jù)集中不確定性的表示方法

不確定性包括數(shù)據(jù)本身的不確定性、近似模型構(gòu)建過程的不確定性，以及系統(tǒng)輸出的不確定性和特征空間的不確定性。其中，數(shù)據(jù)的不確定性主要指屬性的模糊性、屬性值的隨機(jī)性、概念邊界的不分明，具體可表現(xiàn)為語言值數(shù)據(jù)、不一致、缺失和噪聲分布等。本文中模型學(xué)習(xí)過程的不確定性主要是指系統(tǒng)輸出的不確定性，此時(shí)模型學(xué)習(xí)的結(jié)果往往是以概率分布或可能性分布的形式呈現(xiàn)。

以下定義了幾種數(shù)據(jù)的不確定性度量，并說明了計(jì)算方法。為降低計(jì)算耗費(fèi)，均采用盡可能簡單直接的計(jì)算方式。其中數(shù)據(jù)為人工或真實(shí)的待分類數(shù)據(jù)集。決策屬性為樣本的類別標(biāo)號。條件屬性或?qū)傩源頂?shù)據(jù)中樣本的特征。

1.1 不一致性

不一致性指條件屬性相同但決策屬性不同的現(xiàn)象，導(dǎo)致不一致性的原因可能有隨機(jī)性、噪聲等因素。一般地，不一致性的標(biāo)準(zhǔn)為判別屬性相同但決策屬性不同的樣本的個(gè)數(shù)。但由于存在連續(xù)值屬性無法僅通過屬性值的異同來進(jìn)行度量，本文使用基于距離的計(jì)算方法。距離d小于某一閾值ε但決策類不同的樣本定義為不一致樣本，數(shù)據(jù)集中不一致樣本所占總樣本數(shù)的比例為不一致度。其中閾值定義如下：

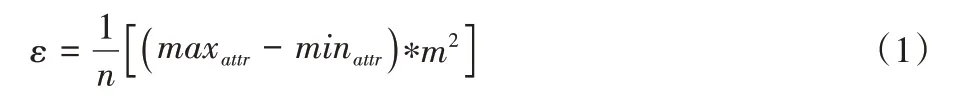
其中：maxattr、minattr為屬性值的最大值和最小值；m為屬性個(gè)數(shù)；n為樣本數(shù)。樣本數(shù)的多少決定數(shù)據(jù)集的密度大小，樣本數(shù)越多則密度越大，閾值應(yīng)越小；屬性維數(shù)越多則樣本間距離增大，閾值相應(yīng)變大。

1.2 邊界復(fù)雜度

邊界復(fù)雜度即為數(shù)據(jù)集中類別之間邊界的復(fù)雜程度，不確定性越大可能邊界越復(fù)雜，體現(xiàn)問題本身的難度。邊界點(diǎn)定義為不能由其周圍的點(diǎn)正確分類的樣本點(diǎn)。本文使用K最近鄰（K-Nearest Neighbor，KNN）方法，查看數(shù)據(jù)集中不能被其K近鄰正確分類的樣本點(diǎn)的個(gè)數(shù)，得到數(shù)據(jù)集中邊界樣本點(diǎn)占總樣本數(shù)的比例即為邊界復(fù)雜度。K近鄰算法使用歐氏距離公式計(jì)算距離最近的K個(gè)樣本。

1.3 模型輸出的不確定性

模型輸出的不確定性即為分類算法對數(shù)據(jù)集進(jìn)行分類后輸出分類類別的不確定性度量。輸出的不確定性反映了數(shù)據(jù)集分類的難度，具體為其中每一個(gè)樣本分類熵的均值。本文使用模糊K近鄰算法對數(shù)據(jù)集進(jìn)行處理得到所有樣本點(diǎn)的針對不同類別標(biāo)簽的權(quán)值，得到權(quán)值矩陣后根據(jù)式（3）計(jì)算得到數(shù)據(jù)集的輸出不確定性：

其中：xij為第i個(gè)樣本點(diǎn)被分到j(luò)類的權(quán)值；m為屬性維數(shù)；n為樣本點(diǎn)總數(shù)。

1.4 線性可分度

目前還沒有單一的方法可以得到一個(gè)數(shù)據(jù)集的線性可分程度，大部分的做法是通過多個(gè)指標(biāo)來進(jìn)行度量。本文通過使用線性分類器對數(shù)據(jù)集進(jìn)行劃分，查看劃分的準(zhǔn)確率作為數(shù)據(jù)集的線性可分度量，即通過使用線性分類器對數(shù)據(jù)分類的效果來衡量問題的線性可分性。線性分類算法優(yōu)化問題公式如下：

1.5 屬性的重疊度

屬性的重疊度指屬性取值的不可區(qū)分度。在分類任務(wù)中，一般認(rèn)為屬性值決定了一個(gè)樣本點(diǎn)被分到哪一類當(dāng)中。若不同類之間的屬性值之間有著比較明顯差異，分類算法就能較好地把不同類區(qū)分開來，而如果不同類間的屬性重疊在一起則會使分類算法的準(zhǔn)確率下降。在相關(guān)工作中類間重疊度的計(jì)算方法是查看待測樣本點(diǎn)與周圍樣本點(diǎn)類別的差異。本文中通過計(jì)算每一個(gè)獨(dú)立屬性的重疊度，將特征空間近似為高維立方體，具體計(jì)算連續(xù)值屬性重疊度的方法如式（5）所示：

其中：m為屬性維數(shù)；lap(attri)為屬性i上取值的重疊范圍，即在屬性i中包含多個(gè)決策類的屬性值范圍；是屬性i的最大值和最小值。

1.6 特征空間的不確定性

前面幾種不確定性度量都是在有監(jiān)督的情況下對分類結(jié)果進(jìn)行的不確定性度量，都需要考慮數(shù)據(jù)集決策類的分布情況。特征空間不確定性則是考察無監(jiān)督的情況下對原數(shù)據(jù)集進(jìn)行聚類得到的結(jié)果，反映了數(shù)據(jù)的特征空間對可能的分類結(jié)果所產(chǎn)生的影響。使用模糊k均值（fuzzyk-means）算法對數(shù)據(jù)集進(jìn)行聚類，得到每一個(gè)樣本點(diǎn)的聚類權(quán)值xi，xi是樣本點(diǎn)i對k個(gè)聚類的權(quán)值向量。再用式（6）計(jì)算數(shù)據(jù)集的聚類不確定性：

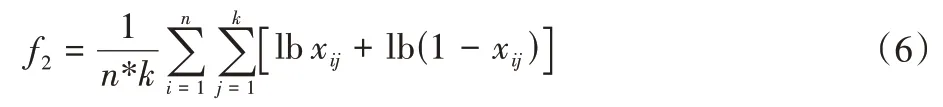
其中：xij為第i個(gè)樣本點(diǎn)對第j個(gè)聚類中心的權(quán)值；k為聚類個(gè)數(shù)；n為樣本點(diǎn)總數(shù)。

2 實(shí)驗(yàn)和結(jié)果

本文在290 個(gè)人工生成的和17 個(gè)真實(shí)數(shù)據(jù)集上，計(jì)算第1 章提出的各種不確定性度量，研究它們和分類性能之間的關(guān)系，以及各指標(biāo)之間的相關(guān)性；發(fā)現(xiàn)不確定性作為數(shù)據(jù)的元特征的重要依據(jù)，以及它們之間的相互關(guān)系。

2.1 人工數(shù)據(jù)集上的相關(guān)性分析

首先在人工生成的數(shù)據(jù)集上對之前提到的幾種不確定性度量進(jìn)行計(jì)算。使用sklearn 庫中的生成數(shù)據(jù)函數(shù)make_circles、make_blobs、make_classification 和make_moons函數(shù)來生成數(shù)據(jù)集，每個(gè)數(shù)據(jù)集包含500 個(gè)隨機(jī)樣本點(diǎn)，屬性維數(shù)為2。通過改變噪聲、類間距離、數(shù)據(jù)團(tuán)大小和屬性范圍等參數(shù)得到不同的數(shù)據(jù)集。

圖1 中是兩組不同參數(shù)所生成的數(shù)據(jù)集，都含有三個(gè)決策類、兩個(gè)屬性。它們的類間距不相同，圖1（a）類間區(qū)別明顯，分類算法很容易可以將不同類別的樣本分辨開來；而圖1（b）中類間距很小甚至為負(fù)，類別之間糾纏在一起，使得分類算法較難以分辨開不同的類別。通過改變函數(shù)中噪聲、聚類大小、密度等參數(shù)可以生成多樣的數(shù)據(jù)集，它們能夠具有明顯不同的不確定性大小。可以在這些數(shù)據(jù)集上計(jì)算第2 章中提出的幾種度量作為數(shù)據(jù)的特性，分析這些特征與分類結(jié)果之間的關(guān)聯(lián)。以圖1 中兩個(gè)數(shù)據(jù)集為例，計(jì)算得到不同特征的度量以及分類準(zhǔn)確率如表1 所示。

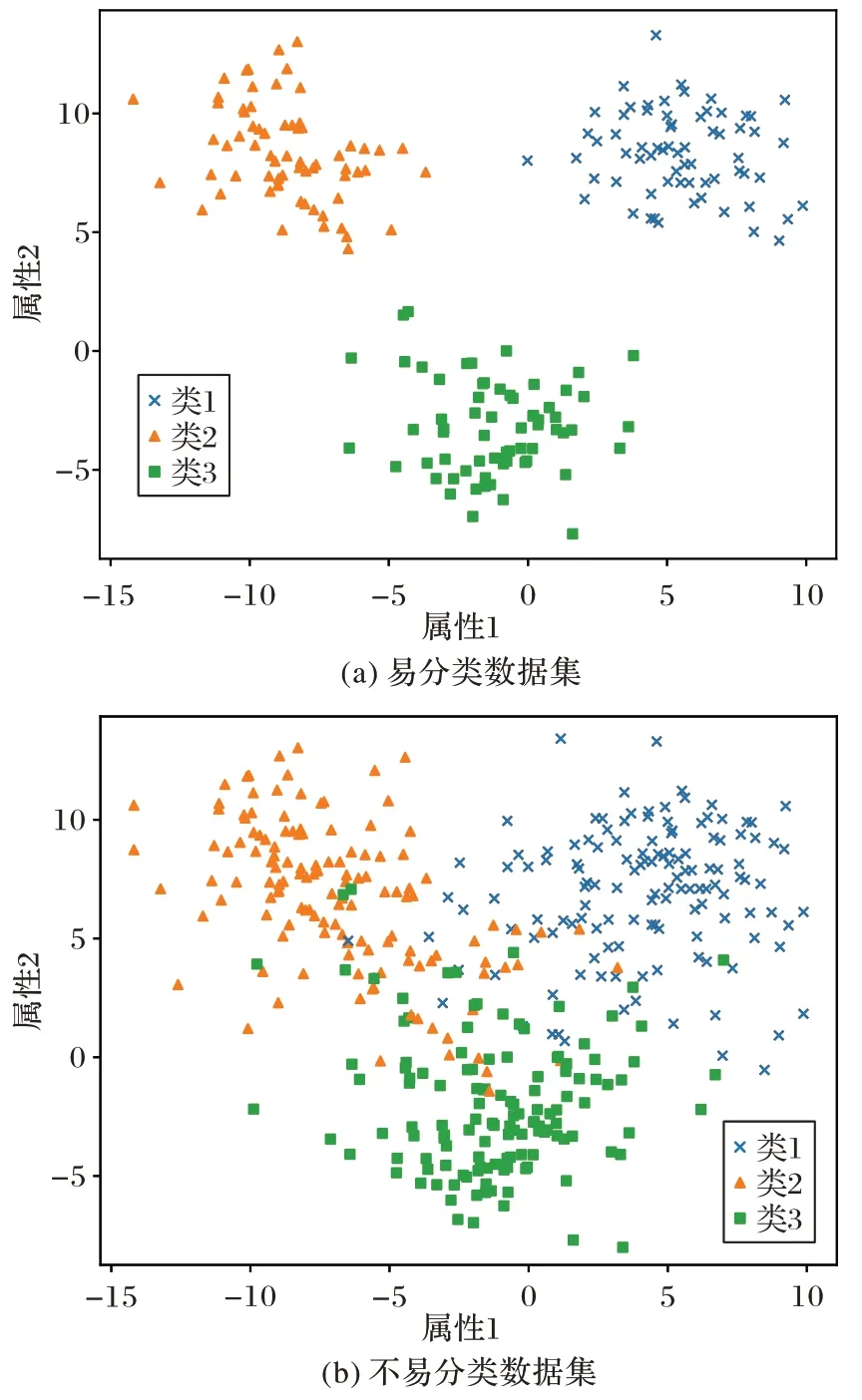
圖1 不同參數(shù)生成的數(shù)據(jù)集Fig.1 Generated datasets with different parameters

表1 圖1中兩數(shù)據(jù)集的不確定性度量Tab.1 Uncertainty measures of easily and difficultly classified datasets

可以看到兩個(gè)數(shù)據(jù)集的特征值具有明顯的差異：易分類數(shù)據(jù)集的多數(shù)特征值明顯大于不易分類數(shù)據(jù)集，線性可分度也高于不易分類數(shù)據(jù)集，分類準(zhǔn)確率也顯示了同樣的結(jié)果。

這樣，通過改變參數(shù)生成不同數(shù)據(jù)。將參數(shù)變化范圍設(shè)為0.2，從小到大每一次改變一個(gè)參數(shù)隨機(jī)生成10 個(gè)數(shù)據(jù)集，共生成290 個(gè)。在這290 個(gè)數(shù)據(jù)上對之前提出的6 種不確定性進(jìn)行度量。同時(shí)對每一個(gè)數(shù)據(jù)集用多個(gè)經(jīng)典分類算法進(jìn)行分類，包括K近鄰算法、神經(jīng)網(wǎng)絡(luò)、支持向量機(jī)和決策樹算法。對每一個(gè)數(shù)據(jù)集輸出這4 分類算法的分類準(zhǔn)確率，之后計(jì)算上述不確定性度量與分類算法準(zhǔn)確率之間的相關(guān)性，查看不確定性與平均分類結(jié)果之間的相關(guān)關(guān)系。計(jì)算相關(guān)性使用皮爾森相關(guān)系數(shù)（Pearson Correlation Coefficient，PCC）：

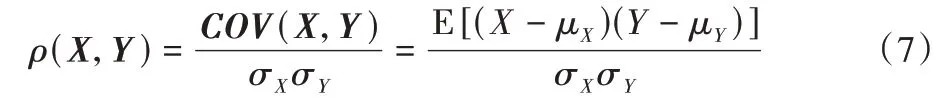
其中：COV（X，Y）為協(xié)方差矩陣；σXσY為標(biāo)準(zhǔn)差的乘積；μX和μY是X和Y的平均值；E[]為正期望。相關(guān)系數(shù)為正表示兩者為正相關(guān)，為負(fù)代表兩者負(fù)相關(guān)。其中：|ρ|<0.3 表示弱相關(guān)性，0.3<|ρ|<0.7 為中度相關(guān)，|ρ|>0.7 代表強(qiáng)相關(guān)關(guān)系。數(shù)據(jù)不確定性與分類結(jié)果具體相關(guān)系數(shù)如表2 所示。

表2 不確定性度量與平均分類結(jié)果的相關(guān)性Tab.2 Correlations between uncertainty measures and average classification results

從表2 可以看出，與分類結(jié)果相關(guān)度最高的是邊界復(fù)雜度和模型輸出的不確定性，相關(guān)度絕對值為0.97；不一致度和特征空間的不確定性相關(guān)度在0.70 左右；相關(guān)度最低的特征是屬性重疊度，相關(guān)度絕對值為0.65。因此不一致度、邊界復(fù)雜度、輸出不確定性和特征空間的不確定性特征與分類結(jié)果之間的關(guān)系為強(qiáng)相關(guān)關(guān)系；屬性重疊度為中等相關(guān)關(guān)系接近強(qiáng)相關(guān)關(guān)系。說明這幾個(gè)特征對分類結(jié)果具有較為顯著的影響。其中不一致度、邊界復(fù)雜度和屬性重疊度為負(fù)相關(guān)關(guān)系，表明這三個(gè)特征越大時(shí)分類結(jié)果的效果越差，與直覺吻合。因?yàn)椴灰恢露却韺傩灾迪嘟珱Q策類不同的樣本比例，邊界復(fù)雜度代表邊界的樣本比例，而屬性重疊度代表類間屬性值重疊區(qū)域占整個(gè)屬性空間的比例。從這三個(gè)特征的定義可以看出它們對分類算法都是負(fù)面影響，因此這些特征的增大意味著分類效果的下降。輸出不確定性、線性分類準(zhǔn)確率和特征空間的不確定性與分類結(jié)果都是正相關(guān)，即這三個(gè)特征值越大分類效果越好。

另外還測量了各個(gè)不確定性度量之間的相關(guān)度，它們之間的相關(guān)度見表3。其中相關(guān)度最高的是輸出的不確定性與邊界復(fù)雜度，它們之間的相關(guān)度絕對值為0.98，說明這兩個(gè)特征度量之間具有極強(qiáng)的相似性，邊界越復(fù)雜意味著不確定性越大；反之亦然。其次是不一致度和特征空間不確定性、不一致度與輸出不確定性之間的相關(guān)性都約為0.7，相關(guān)性較強(qiáng)，其余特征之間的相關(guān)性較低，說明其余特征之間相對獨(dú)立。

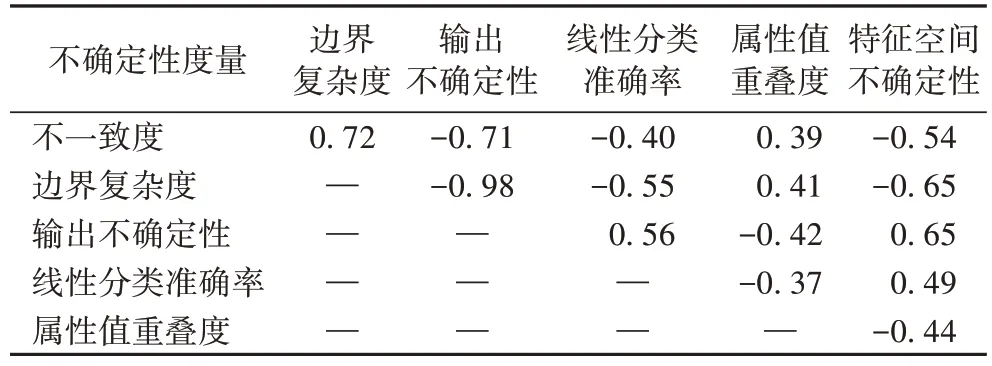
表3 不確定性度量互相之間的相關(guān)性Tab.3 Correlations between uncertainty measures

2.2 實(shí)際數(shù)據(jù)集上的相關(guān)性分析

本文同時(shí)收集了一些真實(shí)數(shù)據(jù)集并在其上進(jìn)行了不確定性特征的測量和分類準(zhǔn)確率的測量，分析它們之間的聯(lián)系，是否與在人工數(shù)據(jù)集上得到的數(shù)據(jù)相仿。真實(shí)數(shù)據(jù)集如表4 所示，所有數(shù)據(jù)均取自UCI 數(shù)據(jù)集，這些數(shù)據(jù)集都是機(jī)器學(xué)習(xí)分類任務(wù)中較為常用的數(shù)據(jù)集，

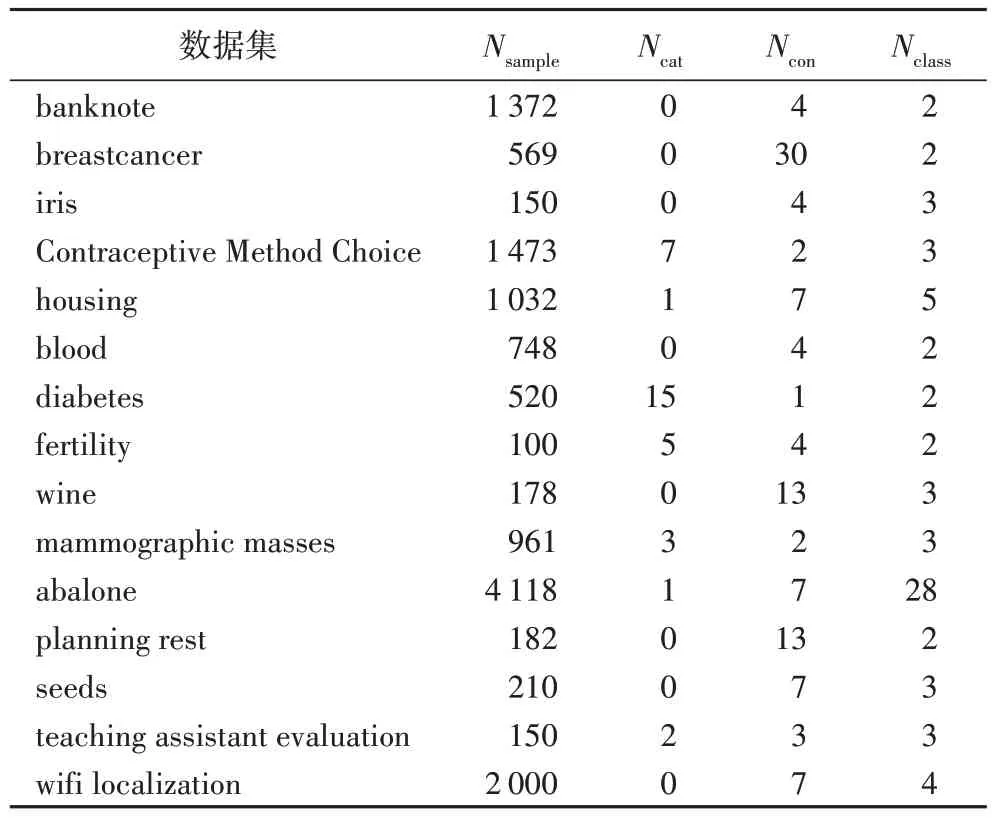
表4 真實(shí)數(shù)據(jù)集Tab.4 Real datasets

其中的樣本都有清晰且數(shù)量適中的決策類，屬性包括離散屬性和連續(xù)屬性，樣例數(shù)適中，便于對數(shù)據(jù)集進(jìn)行后續(xù)處理和用分類算法對數(shù)據(jù)進(jìn)行分類。其中：Nsample為數(shù)據(jù)集中的樣本總數(shù)；Ncat為離散屬性個(gè)數(shù)；Ncon為連續(xù)屬性個(gè)數(shù)；Nclass是數(shù)據(jù)集中的類別數(shù)，共有幾個(gè)不同的類。

由于其中一些真實(shí)數(shù)據(jù)集包含離散屬性，因此對離散的字符型屬性都進(jìn)行了數(shù)值化處理；之后對所有屬性進(jìn)行標(biāo)準(zhǔn)化處理。標(biāo)準(zhǔn)化公式如下：

將原屬性值減去該屬性最小值再除以屬性的范圍即得到標(biāo)準(zhǔn)化后的屬性值。

本文還在真實(shí)數(shù)據(jù)集中添加噪聲來生成含有噪聲的數(shù)據(jù)集，所有噪聲點(diǎn)都為隨機(jī)生成，噪聲點(diǎn)的個(gè)數(shù)約為原數(shù)據(jù)集的1/3，噪聲點(diǎn)隨機(jī)分配類別；之后對所有的數(shù)據(jù)集計(jì)算不確定性度量的取值，最后共得到20 個(gè)數(shù)據(jù)集上的不確定性特征和分類算法準(zhǔn)確率，見表5。其中后方標(biāo)記有（noise）的數(shù)據(jù)是指通過向原始數(shù)據(jù)集中添加隨機(jī)噪聲后得到的。

表5 真實(shí)數(shù)據(jù)集上的不確定性度量與分類準(zhǔn)確率Tab.5 Uncertainty measures and classification results on real datasets

實(shí)驗(yàn)結(jié)果顯示不確定性度量與分類準(zhǔn)確率之間的趨勢大致相同，具體的相關(guān)度見表6，與在人工數(shù)據(jù)集上所得到的相關(guān)性大致相同。綜上可以看出，本文所提出的幾種不確定性度量能夠顯著影響分類器的學(xué)習(xí)性能，可以作為一類重要的元特征。

表6 真實(shí)數(shù)據(jù)集上的不確定性度量與分類準(zhǔn)確率的相關(guān)度Tab.6 Correlation between uncertainty measures and classification accuracy on real datasets

3 結(jié)語

本文從不同方面考慮了數(shù)據(jù)和模型具有的不確定性，具體定義和給出了幾種不確定性的標(biāo)準(zhǔn)和度量方法，并通過實(shí)驗(yàn)驗(yàn)證了它們與分類算法性能之間的關(guān)聯(lián)。其中，不一致性反映了屬性與類別的關(guān)系；邊界復(fù)雜度、輸出不確定性和線性可分度可以表示分類的復(fù)雜程度；屬性重疊度顯示類別之間的重合程度，特征空間不確定性不考慮類別僅對屬性空間進(jìn)行測量。這些度量是從數(shù)據(jù)的屬性與類別的關(guān)系、分布的復(fù)雜程度、問題的難度，以及結(jié)合分類算法后輸出的模糊程度等角度分別衡量數(shù)據(jù)本身的特性，各度量之間沒有明確的理論上的關(guān)聯(lián)，但在結(jié)果上可能有一定的相關(guān)性。大量人工和真實(shí)數(shù)據(jù)集上的結(jié)果表明所提出的幾種不確定性均與使用經(jīng)典分類算法的測試結(jié)果之間具有較強(qiáng)的相關(guān)性。其中模型輸出的不確定性和邊界復(fù)雜度與分類性能的相關(guān)系數(shù)超過0.9，說明邊界越復(fù)雜不確定性越大，問題越困難，分類精度越低。此外還分析了這些度量之間的相關(guān)性，邊界復(fù)雜度、不確定性與不一致度之間的相關(guān)度較高，可以整合為一種不確定性。這些初步分析可以為元學(xué)習(xí)框架下元特征體系的構(gòu)建提供幫助。