基于中心核對齊的多核單類支持向量機

祁祥洲，邢紅杰

（河北省機器學習與計算智能重點實驗室（河北大學數學與信息科學學院），河北保定 071002）

0 引言

單類分類（One-Class Classification，OCC）是機器學習領域一個重要的研究內容，被廣泛地應用于解決如疾病診斷［1］、文本分類［2］、入侵檢測［3］等實際問題。在OCC 中最為常用的兩種方法是單類支持向量機（One-Class Support Vector Machine，OCSVM）［4］和支持向量數據描述（Support Vector Data Description，SVDD）［5］。OCSVM 是Sch?lkopf 等［4］以傳統的支持向量機（Support Vector Machine，SVM）［6］為基礎提出的一種解決異常檢測問題的核方法，其思想是將正常數據在高維特征空間中的像與原點以最大間隔分開，因為在訓練集中沒有任何異常數據的信息，因此將原點看作是異常數據的代表。SVDD 則是在特征空間中使用最小超球將正常數據的像包圍起來。在特定的條件下，能證明OCSVM 與SVDD 等價［5，7］。

近年來，多核學習（Multiple Kernel Learning，MKL）方法獲得了越來越多的關注［8］。與使用單個核函數的核方法相比，使用多個核函數的MKL 方法可以有效地處理數據異構、樣本規模巨大和樣本分布不平坦等問題。在MKL 中，最為關鍵的問題是確定核函數的組合權重。針對該問題，相關學者提出了許多相關的方法及模型。為了解決核函數及其參數的選取問題，同時減小核矩陣的計算量，Bennett 等［9］提出了多重加性回歸核（Multiple Additive Regression Kernel，MARK）算法，在梯度提升及列生成算法的基礎之上，MARK構造了異質核矩陣的列向量，并將它們加入到核集成中。Lanckriet 等［10］利用半定規劃從數據中學習核矩陣，針對遷移學習情形，使用有類別標簽的數據學習一個嵌入空間，然后應用于無類別標簽的數據，測試樣本之間的相似性由訓練樣本及其類別標簽推理得到。實驗結果表明，將多核組合起來產生的分類器取得了和最優的單個分類器接近的性能，此外，優于任何一個單核。Bach 等［11］將二次約束二次規劃（Quadratically-Constrained Quadratic Programming，QCQP）的對偶形式考慮為一個二階錐規劃問題，并利用Moreau-Yosida正則化保持SVM 結構的稀疏性，從而使得生成的公式能夠使用序列最小最優化（Sequential Minimal Optimization，SMO）技術進行求解。Sonnenburg 等［12］將QCQP［11］的對偶形式改寫成一種基于列生成的半無限線性規劃形式，并通過常規的線性規劃求解方法進行求解。實驗結果表明該方法有較強的適應性，可用于解決大規模的核函數組合優化問題，但需要大量的迭代才能收斂到一個較為合適的解。為了解決該問題，Rakotomamonjy 等［13］提出一種稱為簡單多核（simpleMKL）的基于混合范數正則化的MKL 方法，通過加權?2范數正則化的方法來解決MKL 問題，并對核函數的權重增加基于?1范數的約束來提高其稀疏性。實驗結果表明，與文獻［12］的方法相比，simpleMKL 具有更快的收斂速度。

最近，為避免對所有的核函數都分配相同的組合權重，G?nen 等［14］提出了局部多核學習（Localized MKL，LMKL），通過引入門模型（gating model）作為核函數的權重，然后將核函數與門模型相乘所得的組合核函數代入傳統SVM 的優化問題中，并使用梯度下降法進行求解；然而，該方法的訓練過程非常耗時且存在參數冗余問題。為了解決該問題，丁躍［15］在LMKL 的目標函數中增加了正則化項，并在門模型中使用?p范數，成功地解決了LMKL 的參數冗余問題，并進一步提高了其泛化性能。為了提高模糊支持向量機（Fuzzy SVM，FSVM）的抗噪能力，何強等［16］將MKL 引入到FSVM 中，提出模糊多核支持向量機，利用模糊粗糙集和核目標對齊（Kernel Target Alignment，KTA）［17］分別計算每個樣本的隸屬度和每個核函數的組合權重，進而將組合核函數引入到模糊支持向量機中，實驗結果表明該方法有效地提高了FSVM 的分類性能和抗噪能力。針對聚類分析問題，Lu 等［18］提出基于中心核對齊的多核聚類（Multiple Kernel Clustering based on Centered Kernel Alignment，CKAMKC），使用中心核對齊（Centered Kernel Alignment，CKA）的方法將MKL 和聚類統一成一個優化問題，他們將縮放聚類隸屬指標矩陣（scaled cluster membership indicator matrix）作為CKA 的理想核矩陣（idea kernel matrix）并將CKA 用作目標函數，通過兩步迭代優化方法求取核函數的權重和縮放聚類隸屬指標矩陣，進而求出組合核函數。Xue 等［19］將MKL 應用到特征選擇中，在不確定核支持向量機（Indefinite Kernel SVM，IKSVM）的基本框架上，提出一種新的多不確定核特征選擇（Multiple Indefinite Kernel Feature Selection，MIK-FS）方法，該方法對每個特征使用一個不確定基核，然后對核組合系數施加?1范數約束去自動選擇特征，通過一種兩階段交替優化IKSVM 和核組合系數的算法，將原IKSVM 的非凸優化問題轉化為凸差函數規劃，并利用仿射最小逼近將非凸優化問題轉化為凸優化問題，進一步利用分數抽樣方法選擇樣本點來解決大規模問題。此外，還將MIK-FS 擴展到多類特征選擇的情況中。Wang 等［20］提出多Universum 經驗核學習（Multiple Universum Empirical Kernel Learning，MUEKL）框架，利用不平衡數據來生成更有效的Universum 樣本，MUEKL 通過引入正則化的Universum 數據，提出了基本的MKL 框架。引入正則化的目的是調整分類器邊界，使其更接近于Universum 數據，來降低不平衡數據的影響。Oikonomou 等［21］將稀疏貝葉斯學習（Sparse Bayesian Learning，SBL）和MKL 相結合用于穩態視覺誘發電位（Steady State Visual Evoked Potential，SSVEP）的分類，首先在SBL 框架下使用多個線性回歸模型判別SSVEP的類，然后利用變分貝葉斯（Variational Bayesian，VB）方法和MKL 方法學習每個模型的回歸系數，從而將不同的核空間進行組合，并通過實驗驗證了該方法在處理不同核空間的有效性。后來，Wang 等［22］又將MKL 和最近比較熱門的深度學習（Deep Learning，DL）相結合，其中一種方法是將DL 的思想應用到MKL 或者優化過程中。例如Rebai 等［23］提出自適應反向傳播多層MKL 方法，該方法是將前一層中的多個基核組合起來，作為下一層的輸入，然后使用梯度上升優化方法來計算每個核函數的權重，這種方法計算較為簡單，可以成功地優化多層網絡結構。但是上述方法僅限于監督學習情形。

雖然MKL 被廣泛地應用于聚類、二分類和多類分類，然而它被應用于OCC 的研究卻非常少。為了提高傳統OCSVM的分類效果并避免核函數的選取問題，Gautam 等［24］將LMKL應用于OCSVM，與文獻［14］相同，也是利用門模型確定核函數的組合權重，并利用梯度下降法求解相應的優化問題。實驗結果表明，該方法能夠生成較少的支持向量，且具有較好的稀疏性；然而訓練過程非常耗時且存在參數冗余問題。為了避免參數冗余問題，He 等［25］利用多個具有不同參數值的同一種核函數構造組合核函數，采用KTA 方法求取最優組合權重，并利用組合核函數替代傳統OCSVM 中的單個核函數。該方法不僅避免了核函數參數的選取問題，而且訓練過程耗時較短；然而，該方法僅能求取向量維度上的相似性，不能表現出數據之間的相關性，由于沒有將樣本在特征空間中的像進行中心化，因此可能會產生病態矩陣［26］的問題。

為了避免核函數選取問題，同時提高OCSVM 的抗噪聲能力，提出了一種基于中心核對齊的多核單類支持向量機（CKA based Multiple Kernel OCSVM，CKA-MKOCSVM）。

本文的主要工作如下：

1）使用CKA 方法求得核函數的權重。與KTA 相比，CKA 需要對樣本在特征空間中的像進行中心化，使得這些像與原點的距離更近，從而避免產生病態矩陣，使得所提方法在分布較為分散的數據集上也能取得較優的分類性能。

2）用組合核函數替代OCSVM 中的單個核函數，可以解決核函數的選擇問題，同時能夠取得更優的抗噪能力。

1 相關知識

1.1 OCSVM

給定訓練樣本集D=，其中，xi∈Rd，i=1，2，…，N。OCSVM［4］首先通過非線性映射函數φ將樣本點從輸入空間映射到高維特征空間，然后在高維特征空間中最大化樣本點的像與原點之間的間隔，最終求取最優分離超平面wTx-ρ=0，其中：w表示超平面的法向量；ρ表示截距即在高維特征空間中原點和超平面的距離。為了求取最優分離超平面，OCSVM 需要求解下面的優化問題：

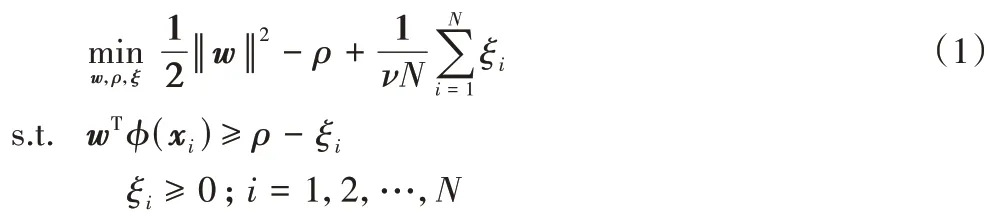
其中：ξ=(ξ1，ξ2，…，ξN)T且ξi是松弛變量；v為折中參數，是邊界支持向量所占比例的上界，也是全部支持向量所占比例的下界。

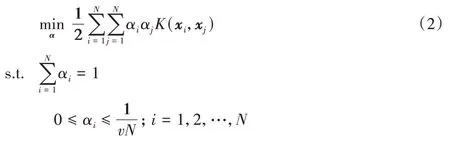
其中：αi是樣本點xi對應的拉格朗日乘子且α=(α1，α2，…，αN)T；K(·，·)為核函數。

對偶優化問題（2）求解之后，對應于αi>0 的樣本xi為支持向量。此外法向量可以表為：

截距ρ可以通過某個支持向量在特征空間中的像φ(xSV)及法線向量w的內積求取，即：

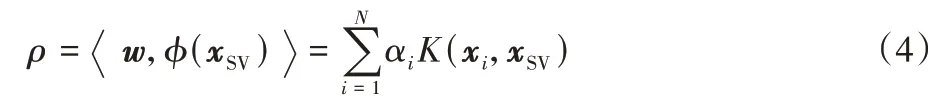
最后，OCSVM 的決策函數可以表示為：

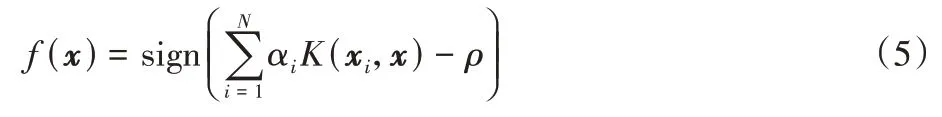
其中：sign(·)為符號函數。當決策函數值為+1 時，待測樣本x被判別為正常數據；當決策函數值為時0，待測樣本x則被判別為異常數據。

1.2 核對齊和中心核對齊

本文采用CKA 的MKL 方法來計算核權重，CKA 由經典的核度量方法——核對齊改進得到。所謂核對齊，就是在兩個核函數（核矩陣）之間或者是核函數（核矩陣）與目標函數（矩陣）之間的相似性度量，是一種經典的核度量方法，它們之間的相似性越高，則它們的一致性也就越高，從而訓練所得的分類器會具有較低的泛化誤差。

定義1核對齊。［17］假設k1和k2是數據集上的兩個核函數，則k1和k2在上核對齊的值為：

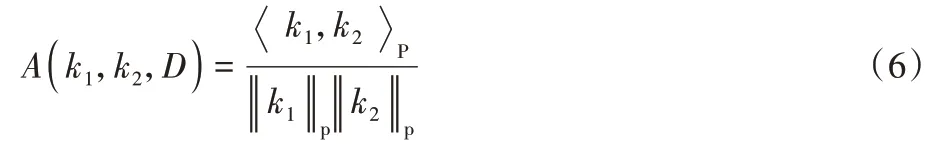
若訓練集中僅包含樣本信息，而無法獲取目標函數知識時，經常會采用經驗核對齊代替核對齊進行度量，其定義如下：

定義2經驗核對齊。［17］假設k1和k2是數據集D={x1，x2，…，xN}上的兩個核函數，對應的核矩陣分別為K1和K2（k∈RN，K∈RN×N），則K1和K2在數據集D上的經驗核對齊定義為：

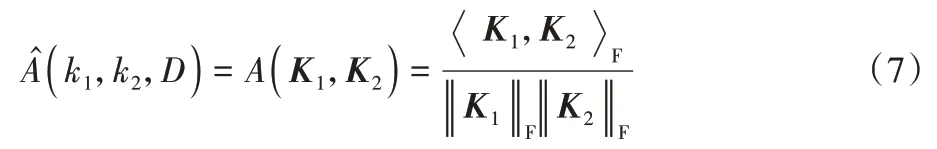
其中：K1和K2均為半正定的核矩陣。是Frobenius內積且‖·‖F表示Frobenius 范數（F 范數），它們分別定義為：

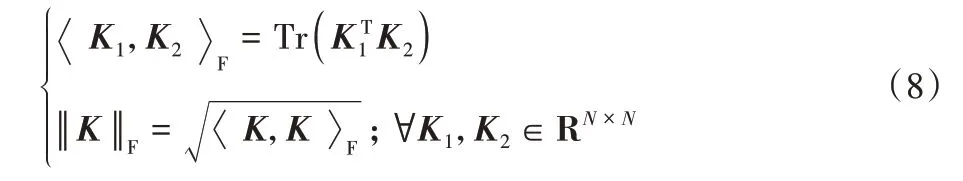
在一定條件下，式（7）所計算出的值是接近式（6）計算出的值［17］，即可利用經驗核對齊代替核對齊。此外，式（7）與余弦度量的公式相同，因此，若越接近于1，K1和K2就越相似。然而，式（7）僅考慮了向量維度上的相似性，而沒有體現數據間的線性相關性。

在特征空間中，若原點遠離樣本的凸包，則核矩陣中元素可能會具有幾乎相同的值，使得核矩陣存在病態問題［26］。為了解決該問題，引入CKA，它與經驗核對齊原理相同，不同之處在于CKA 需要首先在特征空間中進行中心化，然后對中心化后的核矩陣再進行經驗核對齊。

定義3中心核對齊。假設在數據集D={x1，x2，…，xN}上k和k′均為核函數，所對應的核矩陣分別K為和K′，則K和K′在數據集D上的中心核對齊定義為：

2 基于中心核對齊的單類支持向量機

2.1 數學模型

在MKL 中，存在多種不同學習方法來確定核的組合函數，其中常用的方法有以下五種：啟發式［17，27］、固定規則［28］、最優化方法［29］、貝葉斯方法［30］和Boosting 方法［9］，本文采用啟發式學習方法。

所謂啟發式學習方法，這里是指通過最大化CKA 來確定核的權重系數，也就是通過計算核矩陣之間的相關性來確定每個核函數的權重。所提方法包含兩個階段：第一階段確定核組合權重μ；第二階段利用組合權重μ學習多核單類支持向量機。

為了求取最優的核組合權重，需要最大化目標核和理想核之間的相關性，即：

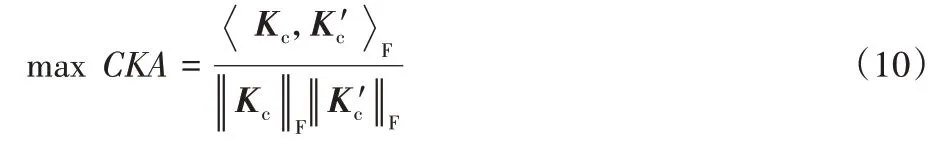
又因為：

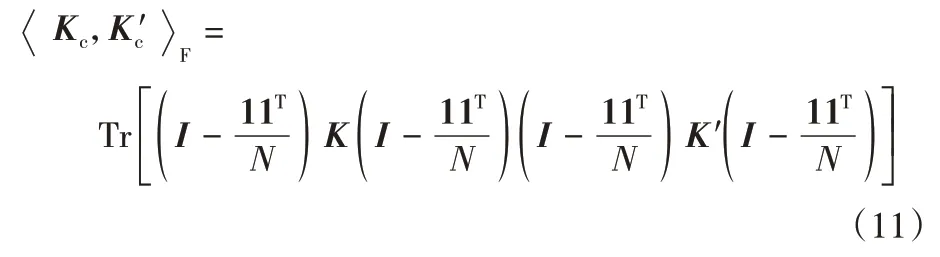
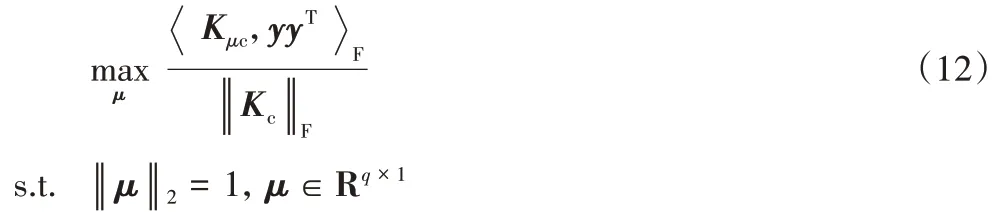
對于優化問題（12），在這里將采用解析式的方法進行求解，首先要將式（12）進行變換，改寫成所需要的形式，即令

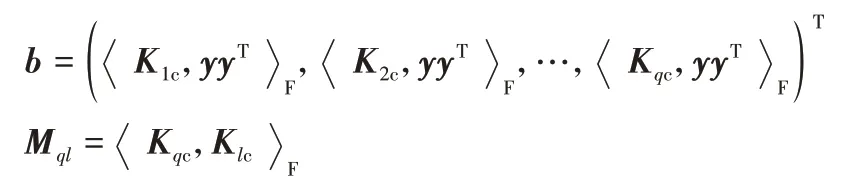
其中：q，l∈[1，p]。所以優化問題（12）可轉化為：

假設μTb>0，在稍后給出證明，對優化問題（13）的目標函數式平方，可得：

因為μ為非零向量，M是非負對稱的半正定矩陣。顯然，優化問題（14）中的目標函數與廣義瑞利商（generalized Rayleigh quotient）相同。可令μ=M-1/2η，代入式（14）可得：

根據瑞利商的性質，式（15）的最優解對應于M-1/2bbTM-1/2的最大特征值，最后可求得解，又因為M和M-1都是半正定矩陣，所以≥0。

將求得的μ引入到OCSVM 中，則優化問題（2）就轉換成如下形式：

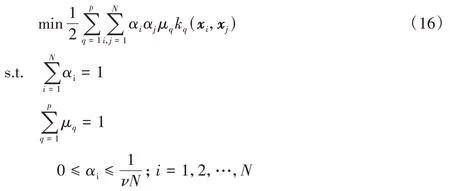
決策函數為：

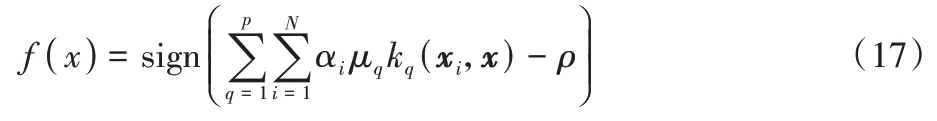
2.2 學習算法

CKA-MKOCSVM 算法的整個訓練過程如下所示：

在算法過程中的第2）～4）步是計算核矩陣，計算復雜度近似為O(pN2)，其中p是核矩陣的數量，N是訓練樣本的數量。第5）步的復雜度近似為O(pN2+pN3)。第7）步的復雜度近似為O(pN2+pN4)，而第8）～9）步是OCSVM 的求解過程，也就是一個二次規劃問題的求解，所以復雜度近似為O(N3)。綜上，整個算法的計算復雜度近似為O(3PN2+(P+1)N3+PN4)。

3 實驗與結果分析

為了驗證本文所提CKA-MKOCSVM 方法的有效性，在20 個UCI 基準數據集上將它與其他五種相關方法進行了比較，UCI 基準數據集是均取自于UCI 機器學習數據庫［31］。其他五種相關方法分別為：基于核目標對齊的多核單類支持向量機（Kernel-Target Alignment based Multiple Kernel OCSVM，KTA-MKOCSVM）［25］、局部多核單類支持向量機（Localized Multiple Kernel OCSVM，LMKOCSVM）［24］、基于徑向基核函數的單類支持向量機（OCSVM with radial basis function kernel function，OCSVM（r））［4］、基于線性核函數的單類支持向量機（OCSVM with linear kernel function，OCSVM（l））［4］以及基于多項式核函數的單類支持向量機（OCSVM with polynomial kernel function，OCSVM（p））［4］。

所使用的UCI 基準數據集均被設計用于二類分類或多類分類問題，為了使它們適用于單類分類，將其中某一類樣本用作正常數據，另一類樣本用作異常數據。從正常數據中隨機選取80%的樣本用作訓練集，剩余的20%正常數據和所有的異常數據用作測試集。所使用的20 個基準數據集的信息概括在表1 中，其中：Nta表示正常樣本個數；Nnon-ta表示異常樣本個數；Nfea表示特征個數；Ntr表示訓練樣本個數；Nts表示測試樣本個數。

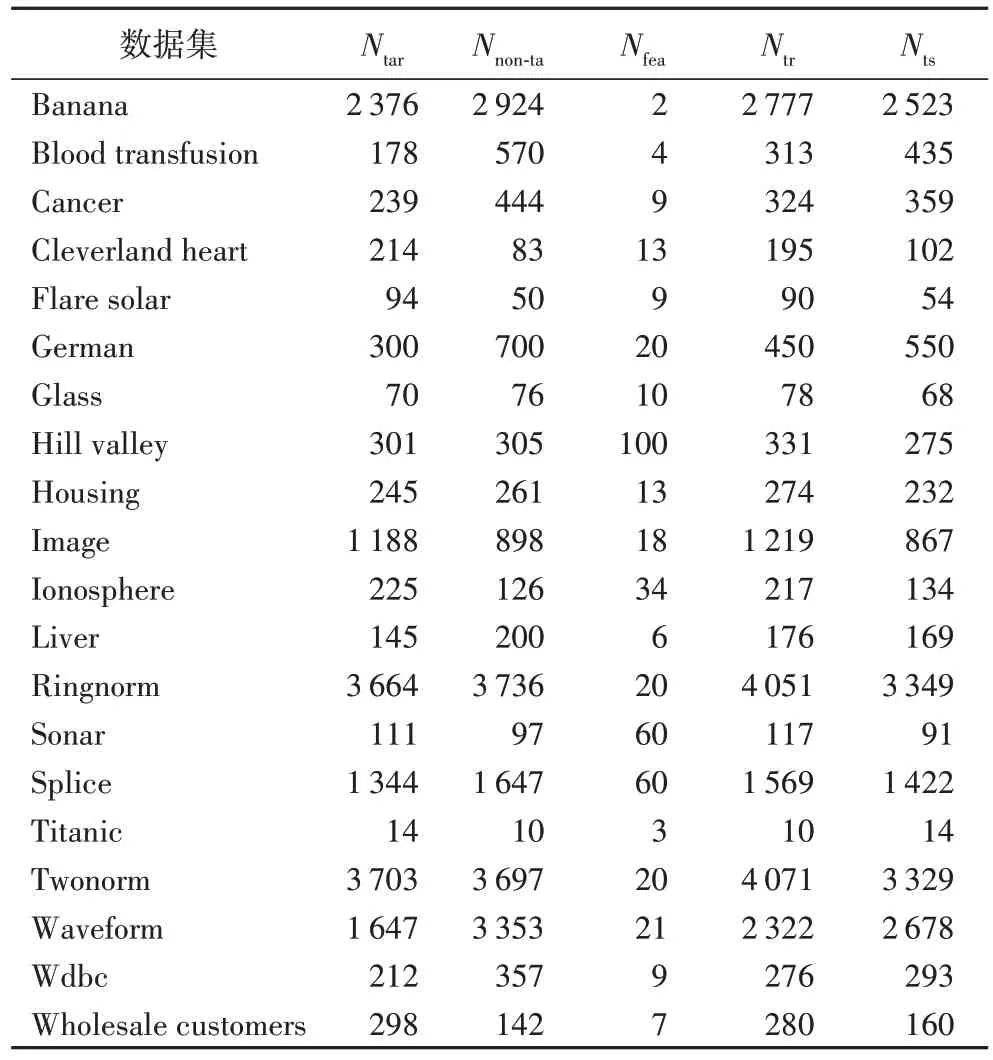
表1 實驗中的數據集Tab.1 Datasets used in experiments

為了構造組合核函數，將選用三種不同類型的常見核函數，即線性核函數、多項式核函數以及徑向基核函數。多項式核函數K(a，b)=(+c)n的參數設置為：γ=1，c=0 和n=4；徑向基核函數K(a，b)=exp(-σ‖a-b‖2)的寬度參數σ在范圍{10-5，10-4，…，103}中將使用窮舉法進行參數選取；OCSVM 折中參數ν在{0.001，0.01，0.02，…，1}中選取。實驗中的參數σ和ν在20 個數據集上的設置如表2所示。

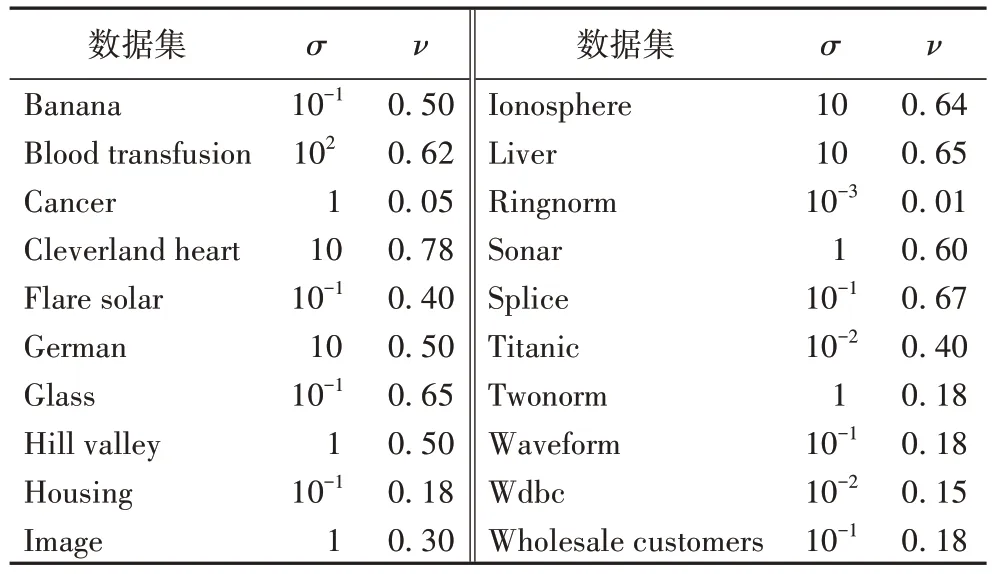
表2 寬度參數σ和折中參數ν在數據集上的設置情況Tab.2 Width parameter σ and compromise parameter ν setting on UCI datasets

此外，在該實驗中由于測試集的樣本類別是非常不平衡的，所以無法使用傳統的準確率來度量，為了降低樣本類別不平衡對于實驗結果的影響，將使用幾何均值（geometric mean，g-mean）來度量單類分類器的分類性能。g-mean［32］可表示為：

其中：Recall表示召回率，即在正常數據樣本上取得的準確率；Specificity表示特異度，即在異常數據樣本上所取得的準確率。

最后，為了減輕訓練集隨機選取的影響，所有方法在每個數據集上均重復20 次實驗，并將測試集上所取得的20 個g-mean 值的平均值用作最終的測試結果。六種方法在20 個基準數據集上的測試結果概括在表3 中。對于每個數據集，測試集上20 個g-mean 值的標準差也概括在表3 中來展示g-mean 值的穩定程度。此外，為了檢驗本文所提CKAMKOCSVM 與其他五種方法在統計上是否存在顯著性差異，對CKA-MKOCSVM 與其他方法分別進行了成對T 檢驗，所得P值也概 括 在表3 中。

從表3 中的測試結果可以看出，CKA-MKOCSVM 在13 個數據集上取得了優于其他五種方法的泛化性能。尤其是在Cancer、Ionosphere、Hill valley、Ringnorm 和Twonorm 五個數據集上，CKA-MKOCSVM 的g-mean 值遠遠高于其他五種方法。由P值可以看出，除Liver 數據集外，所提方法與其他五種方法均存在著顯著性差異。此外，從表3 中的測試結果還可以發現：

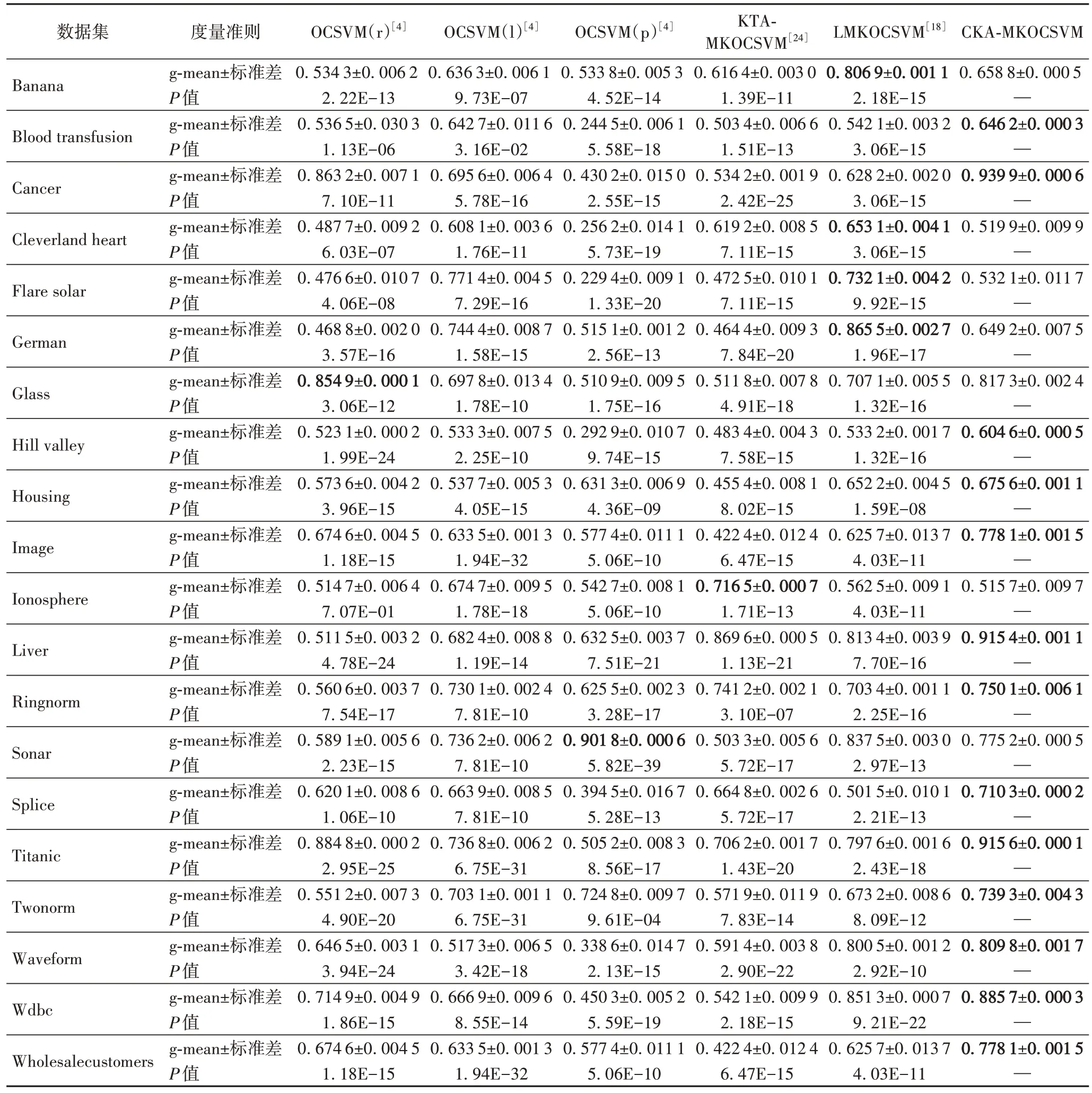
表3 六種不同方法在20個UCI基準數據集上取得的測試結果Tab.3 Test results obtained by six different methods on 20 UCI datasets

1）與單核OCSVM 相比，本文所提CKA-MKOCSVM 將不同類型的核函數組合在一起，并為不同的核函數分配不同的權重值，在處理不同復雜程度的數據時，就能充分發揮不同核函數的優點，從而取得優于單核OCSVM 的性能。

2）與未進行中心化的KTA-MKOCSVM 相比，本文所提CKA-MKOCSVM 將樣本在特征空間中的像進行中心化，使得這些像與原點的距離更近，從而避免產生病態矩陣。此外，CKA-MKOCSVM 對于分布較為分散的數據集具有較優的分類效果。

3）與LMKOCSVM 相比，CKA-MKOCSVM 的優化問題更易求解。LMKOCSVM 利用梯度下降算法進行求解，需要消耗較長的迭代時間，且其門函數還存在參數冗余問題［15］。相比之下，CKA-MKOCSVM 的最優解可以解析求得，無需迭代，LMKOCSVM 需要在目標函數中添加正則化項和使用門函數的范數形式來解決門函數的參數冗余問題；而CKAMKOCSVM 中不存在參數冗余問題。

所以，本文提出的CKA-MKOCSVM 方法在處理一些較為復雜的數據（如高維數據）和在特征空間中分布比較分散的數據都有較為理想的結果。

然而，CKA-MKOCSVM 在Banana、Cleverland heart、Flare solar、German、Glass、Image、Liver 和Splice 上的處理效果并沒有其他原有的五種方法好，其原因主要是對樣本在特征空間中的像經過歸一化和中心化處理后，分布較為密集，使得正常數據和異常數據難以準確區分，從而產生較差的效果。

最后，為了檢驗本文所提CKA-MKOCSVM 的抗噪聲能力，在訓練集加入了5%～30%不同比例的異常數據作為噪聲。圖1 展示了6 種不同方法的測試性能隨噪聲比不同的變化情況。所選用的6 個數據集分別為Cancer、Wdbc、Ionosphere、Wholesale customers、Twonorm、Ringnorm。由圖1中的測試結果可以發現，隨著噪聲比的增加，6 種方法的g-mean 值均呈不同程度的下降趨勢。本文CKA-MKOCSVM方法在6 個數據集上均展示了較優的測試性能，尤其在Cancer、Wdbc、Twonorm 上，其g-mean 值明顯高于其他5 種方法。在Ionosphere 上添加噪聲后，CKA-MKOCSVM 所對應的性能曲線幾乎與OCSVM（r）完全重合，雖然在噪聲比為25%時，OCSVM（r）的g-mean 值較高，但是兩種方法整體上相差很小；同時，CKA-MKOCSVM 在該數據集上優于其他4 種方法。在Ringnorm 上，CKA-MKOCSVM 和KTA-MKOCSVM 的性能曲線幾乎重合，即這兩種方法的測試性能幾乎相同。因此，本文CKA-MKOCSVM 能夠綜合利用三種不同類型核函數的優點，既不用考慮如何選取核函數，又取得較優的抗噪聲能力。

圖1 6種不同方法在6個數據集上的測試性能隨噪聲比不同的變化情況Fig.1 Performance of 6 different methods varying with noise ratio on 6 datasets

4 結語

傳統OCSVM 常常面臨核函數選取的難題。為克服該難題，提出了CKA-MKOCSVM。本文方法的構造過程由兩個階段組成：第一階段，利用CKA 求取核函數的組合權重；第二階段，利用組合核函數替代OCSVM 優化問題中的單個核函數。實驗結果表明，與其他5 種對比方法相比，本文方法具有更優的泛化能力和抗噪聲能力。

雖然該方法能克服OCSVM 的核函數選取問題，但由其算法的計算復雜度分析可發現，該方法的訓練復雜度較高，需要耗費大量時間。在未來工作中需要對組合核的求解方法進行改進，如采用SMO 優化算法［33］等方法；并且本文核函數只選擇了最為常用的3 個，還應該進一步探索其他的核函數并進行組合。