求解工程約束問(wèn)題的新型智能優(yōu)化算法及展望

張孟健，王德光，2，汪 敏，楊 靖，2*

（1.貴州大學(xué)電氣工程學(xué)院，貴陽(yáng) 550025；2.貴州省互聯(lián)網(wǎng)+協(xié)同智能制造重點(diǎn)實(shí)驗(yàn)室（貴州大學(xué)），貴陽(yáng) 550025）

0 引言

典型的工程設(shè)計(jì)問(wèn)題，如管柱設(shè)計(jì)、拉力/壓縮彈簧和壓力容器設(shè)計(jì)［1-2］可以用非線性規(guī)劃（NonLinear Programming，NLP）［3］來(lái)表述，其數(shù)學(xué)模型可表述如下：

其中：X表示決策變量且X=(X1，X2，…，Xn)T；f（X）表示目標(biāo)函數(shù)；gi(X)表示不等式約束；lbj、ubj分別表示決策變量Xj取值的上邊界和下邊界。

對(duì)于非線性規(guī)劃問(wèn)題中，包含了不等式約束問(wèn)題、等式約束問(wèn)題，以及混合式問(wèn)題。針對(duì)解決不等式約束的工程優(yōu)化問(wèn)題，粒子群優(yōu)化（Particle Swarm Optimization，PSO）算法［4］、布谷鳥算法、灰狼優(yōu)化算法等仿生智能優(yōu)化算法取得顯著的成效。

自PSO 算法、遺傳算法（Generic Algorithm，GA）［5］、蟻群優(yōu)化（Ant Colony Optimization，ACO）算法［6］等智能優(yōu)化算法提出以來(lái)，智能優(yōu)化算法在較多的領(lǐng)域得到了廣泛的應(yīng)用，如：工程優(yōu)化、粒子濾波、多目標(biāo)優(yōu)化等。在2010—2020 年近10 年期間，許多新的仿生智能優(yōu)化算法被提出，如：蝙蝠算法（Bat Algorithm，BA）［7］、布谷鳥搜索（Cuckoo Search，CS）算法［8］、灰狼優(yōu)化（Grey Wolf Optimizer，GWO）算法［9］等。在近2018—2020 年期間，群體智能優(yōu)化算法作為人工智能領(lǐng)域的一個(gè)小的分支，得到了較大的發(fā)展。

本文選擇了發(fā)表于2019—2020 年間的6 種新型仿生智能優(yōu)化算法進(jìn)行分析研究，即哈里斯鷹優(yōu)化（Harris Hawks Optimization，HHO）算法［10］、平衡優(yōu)化（Equilibrium Optimizer，EO）算法［11］、海洋捕食者算法（Marine Predators Algorithm，MPA）［12］、政治優(yōu)化（Political Optimizer，PO）算法［13］、黏液霉菌算法（Slime Mould Algorithm，SMA）［14］、堆陣優(yōu)化（Heap-Based Optimizer，HBO）算法［15］。首先對(duì)多個(gè)基準(zhǔn)函數(shù)進(jìn)行測(cè)試，分析它們的尋優(yōu)性能；然后將6 種優(yōu)化算法應(yīng)用于3 種工程優(yōu)化問(wèn)題；最后對(duì)這6 種算法未來(lái)的研究方向進(jìn)行展望。

1 相關(guān)的優(yōu)化算法描述

1.1 HHO算法

HHO 算法的靈感來(lái)自哈里斯鷹探索獵物、突襲的不同攻擊策略［10］。該算法是基于種群的無(wú)梯度優(yōu)化技術(shù)，由于捕獵場(chǎng)景的動(dòng)態(tài)性質(zhì)和獵物的逃跑模式的多樣性，哈里斯鷹可以根據(jù)實(shí)際情況選擇追捕方式，即建立合理的模型，HHO算法可應(yīng)用于任何最優(yōu)化問(wèn)題。

在尋優(yōu)的過(guò)程中，HHO 算法主要有以下階段：探索階段（Exploration phase）、從勘探到開發(fā)的過(guò)渡階段（Transition from exploration to exploitation）、突襲階段（Exploitation phase）；獵物逃逸的能量參數(shù)E采用線性控制策略，且能量參數(shù)初始值E0的取值范圍為［-1，1］，在突襲階段，根據(jù)參數(shù)E的取值可分為：軟圍困和硬圍困兩種。即當(dāng)|E|≥0.5 時(shí)，進(jìn)行軟圍困；當(dāng)|E|<0.5 時(shí)，進(jìn)行硬圍困。

文獻(xiàn)［16］提出了一種改進(jìn)的哈里斯鷹優(yōu)化算法，用于優(yōu)化室內(nèi)到達(dá)時(shí)差（Time Difference of Arrival，TDOA）定位問(wèn)題；文獻(xiàn)［17］針對(duì)參數(shù)E提出了多種不同的改進(jìn)策略，提高HHO 算法求解優(yōu)化問(wèn)題的尋優(yōu)能力和精度。

1.2 EO算法

EO 算法是一種基于控制容積強(qiáng)混合型動(dòng)態(tài)質(zhì)量平衡，從而估計(jì)平衡狀態(tài)的物理啟發(fā)式算法［11］。EO 算法的原理可簡(jiǎn)述為：首先，由四個(gè)最佳粒子的濃度算數(shù)平均值組成平衡池；其次，通過(guò)質(zhì)量平衡方程不斷更新粒子濃度來(lái)達(dá)到尋優(yōu)的效果。在EO 算法的尋優(yōu)過(guò)程中，生成概率（Generation Probability，GP）作為調(diào)節(jié)參數(shù)來(lái)控制參與概率濃度更新的發(fā)生率。

文獻(xiàn)［18］將EO 算法應(yīng)用于含高比例風(fēng)光新能源電網(wǎng)無(wú)功優(yōu)化問(wèn)題，并取得了較好的效果；針對(duì)多級(jí)閾值處理精度差、速度慢等問(wèn)題，文獻(xiàn)［19］提出一種自適應(yīng)均衡優(yōu)化算法用于優(yōu)化多級(jí)閾值優(yōu)化。

1.3 MPA

MPA 是基于捕食Lévy 游走策略和海洋捕食者的布朗運(yùn)動(dòng)以及捕食者對(duì)獵物生物覓食行為的仿生智能優(yōu)化算法［12］。根據(jù)捕食者的覓食行為，MPA 的尋優(yōu)過(guò)程主要有5 個(gè)方面：1）海洋捕食者對(duì)獵物、捕食者豐富區(qū)域分別采用Lévy游走策略和布朗游走，即算法采用Lévy 策略進(jìn)行初始化；2）覓食時(shí)捕食者的Lévy 和布朗游走策略的比例相同，即算法的尋優(yōu)過(guò)程；3）水域渦流或魚類聚集裝置（Fish Aggregating Devices，F(xiàn)ADs）效應(yīng)會(huì)對(duì)捕食者的覓食行為產(chǎn)生影響，即算法尋優(yōu)過(guò)程的調(diào)節(jié)機(jī)制；4）捕食者與獵物運(yùn)動(dòng)速度不同時(shí)，捕食者會(huì)采用不同的覓食策略，即選擇不同的尋優(yōu)策略（局部搜索或全局搜索）；5）捕食者有著良好的記憶，且會(huì)提醒同類成功覓食的區(qū)域，即算法根據(jù)適應(yīng)度值更新位置。文獻(xiàn)［20］針對(duì)水文預(yù)測(cè)預(yù)報(bào)問(wèn)題中的徑流預(yù)測(cè)，提出了一種混合MPA 的自適應(yīng)神經(jīng)模糊推理系統(tǒng)的預(yù)測(cè)方法；文獻(xiàn)［21］提出一種自適應(yīng)變異策略的MPA，用于光伏參數(shù)的識(shí)別，進(jìn)而提高識(shí)別精度。

1.4 PO算法

PO 算法是一種基于政治激勵(lì)的新型優(yōu)化算法［13］。PO算法的結(jié)構(gòu)主要有五個(gè)階段，包括：政黨組建和選區(qū)分配（Party formation and constituency allocation）、選舉活動(dòng)（Election campaign）、政黨轉(zhuǎn)換（Party switching）、政黨間選舉（Inter-party election）和議會(huì)事務(wù)（Parliamentary affairs）。在PO 算法的尋優(yōu)過(guò)程中，政黨組建和選區(qū)分配階段作為初始化，其余四個(gè)階段循環(huán)執(zhí)行至最大迭代次數(shù)或?qū)?yōu)精度。

文獻(xiàn)［22］提出了一種基于基因表達(dá)數(shù)據(jù)的二元政治優(yōu)化器來(lái)解決特征選擇問(wèn)題，并對(duì)多組生物數(shù)據(jù)進(jìn)行分類。

1.5 SMA

SMA 主要是一種模擬黏菌在覓食過(guò)程中的行為和形態(tài)變化的仿生智能優(yōu)化算法［14］。在SMA 中，使用權(quán)重來(lái)模擬黏菌在覓食過(guò)程中產(chǎn)生的正負(fù)反饋，從而形成三種不同的形態(tài)，即接近食物（Approach food）、包圍食物（Wrap food）、擺動(dòng)（Oscillation）。文獻(xiàn)［23］針對(duì)光伏電池的單二極管模型和雙二極管模型，提出了一種基于自適應(yīng)策略的SMA 的參數(shù)估計(jì)方法。

1.6 HBO算法

HBO 算法是受企業(yè)中的等級(jí)結(jié)構(gòu)（Corporate Rank Hierarchy，CRH）啟發(fā)而提出的一種新型優(yōu)化算法［15］。該算法的過(guò)程可分為四個(gè)步驟：1）對(duì)企業(yè)等級(jí)結(jié)構(gòu)（CRH）建模；2）對(duì)下屬與直接上司之間的互動(dòng)進(jìn)行數(shù)學(xué)建模；3）建立同事間互動(dòng)的數(shù)學(xué)模型；4）員工為完成一項(xiàng)任務(wù)而作出的自我貢獻(xiàn)。

1.7 分析小結(jié)

上述的6 種優(yōu)化算法，按其性質(zhì)可以分為三類：1）基于動(dòng)物、生物等覓食行為的群智能優(yōu)化算法（即HHO 算法、MPA、SMA）；2）基于社會(huì)行為的仿生智能優(yōu)化算法（即PO 算法、HBO 算法）；3）基于物理性質(zhì)的仿生智能優(yōu)化算法（即EO算法）。

從6 種算法的結(jié)構(gòu)上可知，HHO 算法、EO 算法和MPA 在尋優(yōu)的機(jī)制上相近，均具有記憶性能；PO 算法是根據(jù)政治選舉的特征，建立合理的模型即能達(dá)到尋優(yōu)的效果；SMA 是一種基于生物覓食行為的優(yōu)化算法，由于在尋優(yōu)時(shí)會(huì)在多個(gè)機(jī)制間轉(zhuǎn)換，增加尋優(yōu)的時(shí)間；而HBO 算法在結(jié)構(gòu)上是基于企業(yè)等級(jí)結(jié)構(gòu)（CRH）的建模，并不能從理論上保證該結(jié)構(gòu)的優(yōu)越性。

2 實(shí)驗(yàn)與結(jié)果分析

為了分析6 種算法的尋優(yōu)能力，選擇了如表1 所示的10種基準(zhǔn)測(cè)試函數(shù)。各算法的參數(shù)設(shè)置如表2 所示，迭代次數(shù)為1 000，維度為50，種群規(guī)模設(shè)為25，每個(gè)測(cè)試函數(shù)獨(dú)立尋優(yōu)30 次。此外，尋優(yōu)仿真測(cè)試的實(shí)驗(yàn)環(huán)境：Windows 7 操作系統(tǒng)，Intel Core i5-4210U CPU @2.4 GHz，4 GB 內(nèi)存，Matlab 2018a。

表1 基準(zhǔn)測(cè)試函數(shù)Tab.1 Benchmark functions

表2 參數(shù)設(shè)置Tab.2 Parameter setting

對(duì)6 種算法的尋優(yōu)性能及其有效性，本文設(shè)計(jì)了2 組對(duì)比實(shí)驗(yàn)：1）6 種優(yōu)化算法對(duì)10 種基準(zhǔn)測(cè)試函數(shù)（5 個(gè)單峰函數(shù)、5 個(gè)多峰函數(shù)）進(jìn)行尋優(yōu)仿真；2）對(duì)3 種不等式約束的工程優(yōu)化問(wèn)題進(jìn)行應(yīng)用比較。

2.1 算法復(fù)雜度

由于測(cè)試平臺(tái)的不同，同一優(yōu)化算法的尋優(yōu)消耗時(shí)間也會(huì)不同。因此，須對(duì)算法的結(jié)構(gòu)進(jìn)行分析，6 種優(yōu)化算法的計(jì)算復(fù)雜度詳見表3。表3 中：N表示算法的種群數(shù)量；T表示算法的迭代次數(shù)；D表示求解問(wèn)題的維度；Cobj表示目標(biāo)函數(shù)的代價(jià)。

表3 不同算法的復(fù)雜度對(duì)比Tab.3 Complexity comparison of different algorithms

2.2 尋優(yōu)結(jié)果

統(tǒng)計(jì)理論在群體智能優(yōu)化算法性能分析中有著廣泛的運(yùn)用。為了驗(yàn)證選擇的6 種優(yōu)化算法的性能，針對(duì)同一基準(zhǔn)函數(shù)獨(dú)立尋優(yōu)測(cè)試30 次。尋優(yōu)結(jié)果的統(tǒng)計(jì)值包括：最優(yōu)值（Best）、最差值（Worst）、平均值（Mean）、標(biāo)準(zhǔn)差（Standard deviation，STD）、尋優(yōu)時(shí)間和中位數(shù)（Median），如表4～5 所示。表4～5 中：除尋優(yōu)時(shí)間外，加粗字體綜合考慮了對(duì)比算法的尋優(yōu)性能；尋優(yōu)時(shí)間僅考慮對(duì)比算法的搜索時(shí)間。

從表4 中可以看出，對(duì)于單峰測(cè)試函數(shù)F1～F5的尋優(yōu)仿真，除函數(shù)F1和F3外，PO 算法的尋優(yōu)結(jié)果均優(yōu)于其他5 種群智能優(yōu)化算法；對(duì)于F1和F3，SMA 雖然能和PO 算法達(dá)到同樣的尋優(yōu)值，但是尋優(yōu)時(shí)間遠(yuǎn)遠(yuǎn)比PO 算法長(zhǎng)，即SMA 的收斂速度差。

表4 基準(zhǔn)測(cè)試函數(shù)尋優(yōu)結(jié)果（單峰）Tab.4 Results of benchmark functions（unimodal）

從表5 中可以看出，針對(duì)測(cè)試函數(shù)F6的尋優(yōu)，HHO 算法均優(yōu)于其他5 種優(yōu)化算法；針對(duì)測(cè)試函數(shù)F7的尋優(yōu)，HHO 算法、PO 算法及SMA 能夠達(dá)到同樣的尋優(yōu)精度，但SMA 的尋優(yōu)時(shí)間最長(zhǎng)，即收斂速度差；針對(duì)測(cè)試函數(shù)F8的尋優(yōu)，除HBO 算法外，其他5 種優(yōu)化算法均能達(dá)到最優(yōu)的尋優(yōu)值，EO算法的尋優(yōu)時(shí)間較短，SMA 的尋優(yōu)時(shí)間較長(zhǎng)；針對(duì)測(cè)試函數(shù)F9和F10的尋優(yōu)，PO 算法的尋優(yōu)結(jié)果在6 種優(yōu)化算法中最佳，此外，HBO 算法的尋優(yōu)時(shí)間較短，但兩個(gè)函數(shù)均沒有達(dá)到最佳的尋優(yōu)值。

表5 基準(zhǔn)測(cè)試函數(shù)尋優(yōu)結(jié)果（多峰）Tab.5 Results of benchmark functions（multimodal）

為了說(shuō)明6 種優(yōu)化算法的收斂速度，對(duì)10 種測(cè)試函數(shù)的尋優(yōu)過(guò)程曲線如圖1～2 所示。圖1（a）～（e）分別表示對(duì)比算法對(duì)5 種單峰測(cè)試函數(shù)的尋優(yōu)曲線趨勢(shì)；圖2（a）～（e）分別表示對(duì)比算法對(duì)5 種多峰測(cè)試函數(shù)的尋優(yōu)曲線趨勢(shì)。橫坐標(biāo)表示對(duì)比算法的最大迭代次數(shù)，均為1 000；縱坐標(biāo)表示對(duì)測(cè)試函數(shù)的尋優(yōu)值的對(duì)數(shù)（lg）。

圖1 六種算法的尋優(yōu)曲線比較（單峰）Fig.1 Comparison of convergence curves of six algorithms（unimodal）

從圖1 中可以看出，對(duì)于單峰函數(shù)F1～F5的尋優(yōu)，除F4外，PO 算法分別在400 次、850 次、450 次和50 次迭代附近達(dá)到了理論最優(yōu)值；而SMA 可以在800 次迭代附近搜索到函數(shù)F1和F3的理論最優(yōu)值。從圖2 中可以看出，PO 算法對(duì)函數(shù)F8和F10的尋優(yōu)均在100 次迭代內(nèi)達(dá)到理論最優(yōu)值。對(duì)于F8的尋優(yōu)，HHO 算法、EO 算法、MPA、PO 算法和SMA 均可以搜索到理論最優(yōu)值；對(duì)于函數(shù)F9的尋優(yōu)，SMA 和PO 算法均在800 次迭代達(dá)到了最優(yōu)值。總的來(lái)說(shuō)，從測(cè)試函數(shù)的統(tǒng)計(jì)結(jié)果和尋優(yōu)收斂曲線均可以看出，PO 算法在6 種對(duì)比算法中的性能較佳，HBO 算法的尋優(yōu)精度較低，可以進(jìn)一步地改進(jìn)研究。

圖2 六種算法的尋優(yōu)曲線比較（多峰）Fig.2 Comparison of convergence curves of six algorithms（multimodal）

2.3 分析小結(jié)

從基準(zhǔn)測(cè)試函數(shù)的仿真結(jié)果來(lái)看，PO 算法能夠達(dá)到測(cè)試函數(shù)的理論最優(yōu)值，且尋優(yōu)時(shí)間較短，即PO 算法的尋優(yōu)精度整體上優(yōu)于其他5 種算法，且收斂速度較快，穩(wěn)定性較好。針對(duì)10 種基準(zhǔn)測(cè)試函數(shù)的尋優(yōu)結(jié)果，在不考慮尋優(yōu)時(shí)間的情況下，6 種優(yōu)化算法進(jìn)行排名：PO >SMA >HHO >EO >MPA >HBO；結(jié)合表3 的各個(gè)算法的計(jì)算復(fù)雜度來(lái)看，SMA的收斂速度較差，在確保尋優(yōu)精度的前提下對(duì)SMA 進(jìn)行改進(jìn)。由于HBO 算法的尋優(yōu)精度低，需要進(jìn)一步地改進(jìn)來(lái)增加尋優(yōu)精度。

此外，各優(yōu)化算法的理論性研究不足，需要從理論上對(duì)提出的算法進(jìn)行收斂性分析［24］。對(duì)于優(yōu)化算法的改進(jìn)，建議如下：算法的種群可以采用混沌理論來(lái)提高其遍歷性；控制參數(shù)同樣可以運(yùn)用混沌映射或非線性策略進(jìn)行調(diào)節(jié)，提高算法的尋優(yōu)性能；混合不同的優(yōu)化算法優(yōu)點(diǎn)來(lái)提高被改進(jìn)算法的尋優(yōu)精度等［25］。

3 工程約束問(wèn)題的應(yīng)用對(duì)比

為進(jìn)一步分析6 種優(yōu)化算法的性能，選擇了工程中3 種非線性約束優(yōu)化問(wèn)題：工字梁設(shè)計(jì)問(wèn)題、三桿桁架設(shè)計(jì)問(wèn)題和減速器設(shè)計(jì)問(wèn)題。這3 種工程優(yōu)化問(wèn)題的具體描述詳見文獻(xiàn)［2］。6 種算法的種群數(shù)量設(shè)置為25（其他參數(shù)設(shè)置詳見表2）；迭代次數(shù)設(shè)為1 000；對(duì)求解每個(gè)工程約束優(yōu)化問(wèn)題分別獨(dú)立運(yùn)行30 次；并分析其尋優(yōu)結(jié)果的統(tǒng)計(jì)值：最優(yōu)值、最差值、平均值、標(biāo)準(zhǔn)差、尋優(yōu)時(shí)間。

3.1 工字梁設(shè)計(jì)問(wèn)題

工字梁設(shè)計(jì)問(wèn)題［2］的目標(biāo)是在承受最小的工字梁的垂直擾度，同時(shí)滿足給定載荷下的截面面積和應(yīng)力約束。當(dāng)梁長(zhǎng)L=200 cm，彈性模量H=2×104kN/cm2，最大彎曲力P=600 kN 和Q=50 kN 時(shí)，垂直撓度f(wàn)（x）=PL3/48HI最小（單位為cm），其中：I為使用材料的截面慣矩（單位為cm4）。

該問(wèn)題的目標(biāo)函數(shù)及約束條件表述如下：

其中：決策變量（x1，x2，x3，x4）分別對(duì)應(yīng)工字梁設(shè)計(jì)的上、下梁的寬度（b）、上梁和下梁底部之間的高度（h）、銜接梁的寬度（tw），以及上、下梁的厚度（tf）。各變量的取值范圍為：10≤b≤50，10≤h≤80，0.9≤tw≤5，0.9≤tf≤5。

根據(jù)該問(wèn)題的目標(biāo)函數(shù)及約束條件，6 種算法的計(jì)算結(jié)果如表6～7 所示。

表6 工字梁設(shè)計(jì)的最優(yōu)結(jié)果對(duì)比Tab.6 Comparison of best results of I-beam design

表7 工字梁設(shè)計(jì)的統(tǒng)計(jì)結(jié)果對(duì)比Tab.7 Comparison of the statistical results of I-beam design

對(duì)于工字梁設(shè)計(jì)問(wèn)題，從表6～7 可知：6 種算法的均值（Mean）排名為：EO=MPA=SMA >HHO >PO >HBO；對(duì)應(yīng)的標(biāo)準(zhǔn)差（STD）可以看出MPA 的穩(wěn)定性優(yōu)于EO 算法，EO 算法優(yōu)于SMA；然而在尋優(yōu)結(jié)果相近的情況下，EO 算法的尋優(yōu)時(shí)間比MPA 和SMA 的尋優(yōu)時(shí)間短。

3.2 三桿桁架設(shè)計(jì)問(wèn)題

三桿桁架設(shè)計(jì)問(wèn)題［2］的目標(biāo)是在靜壓下桁架的體積應(yīng)盡量減小，且滿足每個(gè)桁架構(gòu)件上受應(yīng)力（σ）約束。該問(wèn)題可轉(zhuǎn)化為最佳橫截面積（A1，A2）問(wèn)題，其目標(biāo)函數(shù)及約束條件表述如下：

針對(duì)三桿桁架設(shè)計(jì)問(wèn)題的目標(biāo)函數(shù)及約束條件，6 種算法的計(jì)算結(jié)果詳見表8～9。

表8 三桿桁架設(shè)計(jì)的最優(yōu)結(jié)果對(duì)比Tab.8 Comparison of best results of three-bar truss design

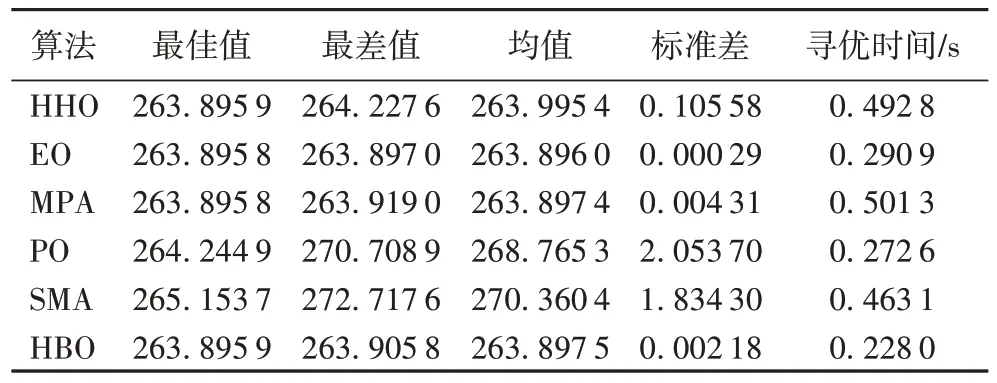
表9 三桿桁架設(shè)計(jì)的統(tǒng)計(jì)結(jié)果對(duì)比Tab.9 Comparison of the statistical results of three-bar truss design

對(duì)于三桿桁架設(shè)計(jì)問(wèn)題，從表8～9 可知：6 種算法的均值（Mean）排名為：EO=MPA >HHO=HBO >PO >SMA；對(duì)應(yīng)的標(biāo)準(zhǔn)差（STD）可得EO 算法的穩(wěn)定性優(yōu)于HBO 算法；然而HBO 算法的尋優(yōu)時(shí)間比EO 算法的尋優(yōu)時(shí)間短。

3.3 減速器設(shè)計(jì)問(wèn)題

減速器設(shè)計(jì)問(wèn)題［2］是典型的機(jī)械方面的優(yōu)化問(wèn)題，其目標(biāo)是使減速器的總重量最小。該問(wèn)題包括面的寬度（x1），齒的模量（x2），小齒輪上的齒數(shù)（x3），軸承之間的軸1 的長(zhǎng)度（x4），軸承之間的軸2 的長(zhǎng)度（x5），軸1 的直徑（x6），軸2 的直徑（x7）。約束條件主要有：齒輪齒的彎曲應(yīng)力、表面應(yīng)力、軸1 和2 的橫向偏轉(zhuǎn)傳遞的力、軸1 和2 之間的應(yīng)力等。

該問(wèn)題的目標(biāo)函數(shù)及約束條件表述如下：

其中：2.6≤x1≤3.6，0.7≤x2≤0.8，17≤x3≤28，7.3≤x4≤8.3，7.8≤x5≤8.3，2.9≤x6≤3.9，5≤x7≤5.5。

針對(duì)減速器設(shè)計(jì)問(wèn)題的目標(biāo)函數(shù)及約束條件，6 種算法的計(jì)算結(jié)果如表10～11 所示。

表10 減速器設(shè)計(jì)的最優(yōu)結(jié)果對(duì)比Tab.10 Comparison of best results of speed reducer design

表11 減速器設(shè)計(jì)的統(tǒng)計(jì)結(jié)果對(duì)比Tab.11 Comparison of the statistical results of speed reducer design

對(duì)于減速器設(shè)計(jì)問(wèn)題，從表10～11 可知：6 種算法的均值（Mean）排名為：EO=MPA=HBO >SMA >PO >HHO；對(duì)應(yīng)的標(biāo)準(zhǔn)差（STD）可以看出EO 的穩(wěn)定性優(yōu)于HBO 算法，EO 算法優(yōu)于MPA；然而在尋優(yōu)結(jié)果相近的情況下，HBO 算法的尋優(yōu)時(shí)間比EO 算法和MPA 的尋優(yōu)時(shí)間短。

4 結(jié)語(yǔ)

針對(duì)近兩年來(lái)提出的6 種新型智能優(yōu)化算法在求解工程約束問(wèn)題上的應(yīng)用：首先，基于對(duì)基準(zhǔn)測(cè)試函數(shù)的仿真實(shí)驗(yàn)，分析了6 種算法的收斂速度、尋優(yōu)精度和穩(wěn)定性等性能；然后，將6 種算法用于求解3 種典型的非線性約束工程優(yōu)化問(wèn)題并分析性能。

基準(zhǔn)測(cè)試函數(shù)的尋優(yōu)結(jié)果表明：PO 算法的尋優(yōu)精度整體上優(yōu)于其他5 種算法，且收斂速度較快、穩(wěn)定性較好；在不考慮尋優(yōu)時(shí)間的情況下，6 種優(yōu)化算法進(jìn)行排名：PO>SMA>HHO>EO>MPA>HBO；結(jié)合各算法的計(jì)算復(fù)雜度和尋優(yōu)的消耗時(shí)間，SMA 的收斂速度較差，在確保尋優(yōu)精度的前提下對(duì)SMA 進(jìn)行改進(jìn)。由于HBO 算法的尋優(yōu)精度低，需要進(jìn)一步地改進(jìn)來(lái)提升尋優(yōu)精度；從尋優(yōu)的結(jié)果來(lái)看，其他的算法亦存在收斂精度較低、收斂速度較慢、穩(wěn)定性差等問(wèn)題，因此需要進(jìn)一步地改進(jìn)研究。改進(jìn)的方法可采用反向?qū)W習(xí)策略、非線性控制策略、混沌映射理論、混合算法等。從工程優(yōu)化問(wèn)題的求解來(lái)看，不同的優(yōu)化算法對(duì)于不同的工程問(wèn)題，其尋優(yōu)的性能存在差異，即符合“No free lunch”理論［26］。

在未來(lái)的研究中，可以將收斂性能較好的算法應(yīng)用于不同的實(shí)際問(wèn)題，如：參數(shù)估計(jì)、特征選擇與分類、非線性規(guī)劃等工程問(wèn)題；鑒于新型智能優(yōu)化算法的理論性研究不足，需要進(jìn)一步從理論上去分析和證明提出的智能優(yōu)化算法的收斂性。