循環程序的界函數合成

譚 旺，李 軼

（1.中國科學院重慶綠色智能技術研究院，重慶 400714；2.中國科學院大學計算機科學與技術學院，北京 101408）

0 引言

循環程序終止性的分析與驗證已成為程序驗證領域的一個熱點問題，并且引起了國內外許多學者的關注［1-3］。循環程序的終止性是一個不可判定的問題［4-6］，它的解決方案可以廣泛地提高軟件的可靠性以及程序員的工作效率。目前有幾種優秀的工具應用于不同計算模型的自動終止性驗證分析［7-8］。證明給定循環程序是否是可終止的有著許多的研究方法，比如特征值法［9］、秩函數法［10-17］、界函數法［18-22］、抽象解釋［23-25］以及不變式［26-27］等。

秩函數法作為終止性分析的主流方法已經得到了廣泛的研究。當前求解秩函數的方法大多局限于線性秩函數［10-13］或者多項式秩函數［14-17］的求解。本文主要考慮給定循環的界函數計算問題，在循環程序體內設置一個循環計數器變量c，然后計算循環計數器變量的上界，不難看出，循環計數器變量的上界實際上就是某給定初始值的循環迭代次數的一個上界。如果對于任意滿足循環條件的初始值，其對應的循環計數器變量均存在上界，那么該循環程序一定是可終止的。具體地，本文首先設定一個界函數模板并且將界函數的求解問題轉化為線性二分類問題，然后利用支持向量機（Support Vector Machine，SVM）［28］探測分類超平面獲得模板系數從而得到候選的界函數，最后將候選界函數進行優化并采用符號驗證工具Redlog 對其進行驗證。與基于秩函數的循環程序終止性驗證問題相比，盡管計算循環程序計數器變量十分困難，即界函數方法是一個更為復雜的問題［29］，但是，本文的實驗結果表明，對于某些不能通過計算線性秩函數或線性多階段秩函數來證明其終止性的循環，通過本文方法卻可以找到其線性界函數，從而證明這些循環的終止性。

1 預備知識

本文主要考慮如下形式循環，即：

其中：a=(a1，a2，…，ak)T∈Rk是一個k維向量，不等式≤0 是程序的循環條件，而=fi(a)中的表示ai在經過一次循環迭代后的值，并且=fi(a)是循環的賦值表達式，其中fi(a)是連續函數。

令a′=以及f(a)=(f1(a)，f2(a)，…，fk(a))T，因此，可得a′=f(a)。

例1 考慮以下來自文獻［12］的循環：

在這個循環中，循環條件是4a1+a2≥1，循環區域為Ω={a∈R2：4a1+a2≥1}；賦值語句是=-2a1+4a2以及=4a1。

1.1 界函數

如果一個循環程序在滿足循環條件內的所有初始值上均是可終止的，那么該循環程序便是可終止程序。對于可終止循環程序，滿足循環條件的初始點在有限次迭代之后必然跳出Ω。給定一個可終止循環P，令C(a)：Ω→N 為初始值輸入點a在循環P中的有窮次迭代次數。為方便，本文稱C(a)為Ω（或程序P）的迭代次數函數。對?a∈Ω，有C(a)≥1。

一般地，要精確計算C(a)是困難的。為此引入界函數的概念來逼近C(a)。函數的定義如下：

定義1給定循環程序P。令C(a)為程序P上的迭代次數函數。如果存在函數τ(a)，使得?a∈Ω，有τ(a)≥C(a)，則稱τ(a)為程序P的界函數。

從定義可以看出，對一個循環程序，若能夠求解出其對應的界函數，那么初始值的迭代次數均會有一上界（即：該初始值必在有窮次迭代后跳出Ω）。因此，如果任意初始值a∈Ω均能夠在有窮次迭代后跳出Ω，那么該循環程序就是終止的。

1.2 支持向量機

支持向量機［30］是一種對數據進行二元分類的廣義線性分類器，提出后便得到了廣泛的關注和持續的發展。此外，由于支持向量機方法已經逐步理論化并成為統計學習理論的一部分［31］，并且是建立在結構風險最小原理基礎上的，因此，其堅實的理論基礎以及良好的特性使得現在很多領域都對其有著廣泛的應用，例如：模式識別、概率密度估計和回歸估計等。本文將界函數計算問題歸結為線性二分類問題，從而可以利用支持向量機探測候選界函數。

假設給定訓練樣本集D={(x1，y1)，(x2，y2)，…，(xk，yk)}，其中yi∈{-1，+1}。樣本空間的劃分問題即是否能夠找到一個超平面wTx+b=0 使得這兩類點分離，其中：w為法向量，決定了超平面的方向，而b則是位移項。支持向量機算法的作用便是能夠找到向量w以及實數b使得(xi，yi)∈D滿足［32］：

特別地，支持向量機能夠找到向量w使得：

1.3 不變式

程序不變式指的是程序變量之間滿足的并且不隨程序狀態遷移發生變化的關系。當前，線性循環不變式以及多項式循環不變式的生成都取得了很大的進展，構造程序不變式已成為軟件自動驗證領域內的重要研究內容。程序不變式的一般定義如下：

定義2給定帶初始值的循環程序P0：

如果存在表達式I(a)滿足下列兩個條件：

那么，I(a)稱為循環P0的循環不變式。其中：θ表示初始點集合；initial 條件表明循環的第一次迭代前，循環不變式為真；consecutive 條件表明如果在循環體內某次迭代前為真，那么迭代后仍保持為真。

2 界函數的合成

本章描述了循環程序界函數的合成方法，主要包括了如何將合成界函數的問題轉換為分類問題，如何構建訓練集，如何獲得分類超平面來確定候選界函數，如何對候選界函數進行優化，以及如何構建測試集。

2.1 問題轉換

本節將會介紹如何將界函數的求解問題轉化為分類問題。

令a=(a1，a2，…，ak)T∈Rk，其中k為Ω中點的維數。令τ(a)=wT·V(a)為循環程序P的界函數，其中wT為參數。τ(a)便是所設置的界函數模板，其中，V(a)由單項式或多項式所構成。

根據迭代函數的定義，可得

又由界函數的定義，有

也即：對?a∈Ω，可得

故?a∈Ω，可得

綜上所述，界函數的計算問題可以被歸結為負類點u-與集合T的超平面劃分問題，而這是一個典型的二分類問題。由于T是無窮點集，為了便于利用SVM 去求解該超平面，需要首先從T中抽取有限個樣本點構成T0，故負類點u-與集合T的超平面劃分問題便被轉化為u-與集合T0的超平面劃分問題。若u-與有限點集T0之間的超平面一旦被計算，就可以得到了一個“候選的界函數”，然后利用Redlog 工具去驗證該候選界函數是否是真的界函數。

例2 考慮例1 所示循環。

本例中設置其界函數模板為：

τ(a1，a2)=w1·(a1+1)2+w2·(a2+1)2+w3

即：

由T的定義，

故可得兩類點集合為：

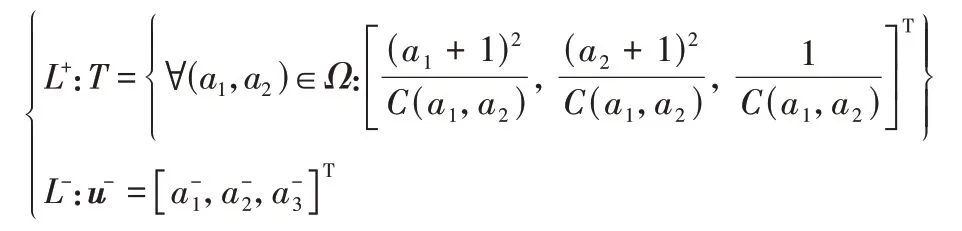
即：本文需要找到一個線性超平面L(u)：=wT·u=0 將u-與集合T嚴格分離。

2.2 超平面的求解

從2.1 節可知，本文將候選界函數的求解問題轉化為一個u-與T0之間的二分類問題，即找到u-與T0之間的超平面L(u)：=wT·u=0，從而獲得候選界函數的系數wT，進而得到候選的界函數τ(a)=wT·V(a)。為此，本文首先需要構造訓練集，而構造訓練集的一般過程分為兩步：一是構造正類點集合T0和負類點u-；二是對所獲得的樣本點打上標簽。過程如下：

1）正類點集合T0和負類點u-。

首先需要在循環區域Ω中自定義采樣區間并采n個樣本點，即針對每一個變量自定義取值范圍，其中i∈{1，2，…，k}，而這里的以及n為可調參數；然后針對每一個采樣點，求解出其精確迭代次數，之后通過T=映射到U空間，本文將該映射關系令為H，這樣便獲得了正類點集合T0，其次，還需要找到一個負類點u-，滿足u-?T，而實驗中只需要找到一個這樣的點作為負類點即可。這樣的點是容易選取的。

例3 考慮例1 中的循環（續例2）。

由于該循環的循環區域Ω為：4a1+a2≥1，因此需要在像空間U空間外找尋一個樣本點作為反例點u-。本例中選取反例點為（0，0，1）。由于該循環區域Ω為無界區域，因此為構造樣本集T0需要在Ω中自定義一個有界的采樣區間進行采樣，這里設定采樣區間為a1∈(-100，100) 以及a2∈（-100，100）。

2）打標簽。

在得到樣本點之后，還需要對樣本點打上標簽，正例點打上+1，負例點打上-1。

算法1 描述了求解樣本點真實迭代次數的過程，針對某一給定樣本點以及循環程序，求解出該樣本點在循環程序中的迭代次數。

算法2 描述了訓練集的構建過程。首先確定采樣個數，然后針對所采樣本點用上述的映射關系映射到U空間得到集合T0，之后選取一負類點u-使之滿足u-∈L-，最后分別對正類點以及負類點打上標簽。

在得到訓練集xtrain以及ytrain之后，便可以通過SVM 進行訓練。從上述構造訓練集的過程可以看出，無論所選取的界函數模板為何形式，都可以將樣本點映射到U空間，使得界函數的計算問題可以直接轉化為一個線性二分類問題。因此在利用SVM 的訓練過程中均采用線性核函數，在用訓練集進行訓練之后，所求得超平面如下：

且對?(u1，u2，…，ud)∈T0，有

若1-wd+1>0，則由式（9），對?(u1，u2，…，ud)∈T0，有

可得到一個新的超平面L(u)=WT·u，且對?u∈T0，有L(u)≥1，即T0在L(u)的正半部分。

當1-wd+1<0 時，將重新構建訓練集進行訓練。

因此根據事先設定的模板，便可以得到候選界函數為：

例4 對于例1 中的循環程序（續接例3）。

將例3 所得到的訓練集代入SVM 模型進行訓練之后，可以得到分類超平面系數為：

因此可以得到：

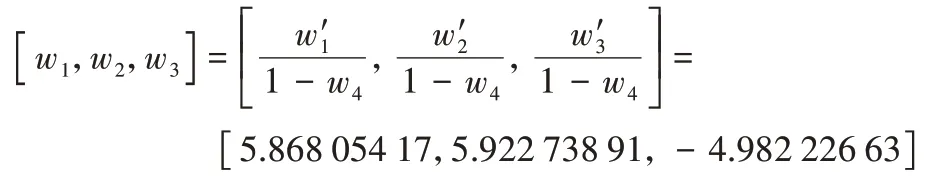
則候選界函數為：

τ(a1，a2)=5.868 054 17(a1+1)2+5.922 738 91(a2+1)2-4.982 226 63

2.3 候選界函數的優化

通過上述對超平面的求解，可以得到界函數的模板系數，進而得到候選的界函數。此外，根據界函數自身獨特的性質，可以對候選界函數通過一些方法進行優化，使其有更大的可能通過后續的精確驗證。

根據界函數的性質，界函數滿足：?a∈Ω，τ(a)≥C(a)。因此，本文將候選的界函數進行放大操作得到τ′(a)，使其滿足：

因此，如果能夠通過優化得到τ′(a)，那么本文最終只需驗證τ′(a)是否是真正的界函數，即驗證τ′(a)≥C(a)。

本文將分為以下幾個情況對候選τ(a)進行處理：

1）令出現在τ(a)中的程序變量集S={}，其中ij∈{1，2，…，k}。如果存在ij，使得在Ω上恒為正或者恒為負，那么就可以將這種情形下的τ(a)進行優化放大處理。

3）對于候選界函數中的常數項，可以始終對其進行放大處理：一是當所求的常數項范圍在（-1，1），可以直接將其放大至1；二是當所求的常數項范圍為(-∞，-1)，將其上取整再取平方值。通過放大常數項系數，使得候選的界函數有更大的可能通過后續的驗證。

例5 考慮例1 中的循環，續接例4。

由于其程序變量在Ω上有正有負，所以將該程序變量在模板中系數設為2，由設置的界函數模板易得，變量項(a1+1)2與(a2+1)2均為正項，因此其系數可以進行放大處理（如：向上取整）。

根據例4 所得的超平面系數，可以得到候選界函數為，

τ(a1，a2)=5.868 054 17(a1+1)2+5.922 738 91(a2+1)2-4.982 226 63

于是將所得的候選界函數變量項前的系數進行向上取整，可得：

τ′(a1，a2)=6(a1+1)2+6(a2+1)2-4.982 226 63

再對常數項進行處理，可得最終的候選界函數為：

τ″(a1，a2)=6(a1+1)2+6(a2+1)2+25

2.4 測試集

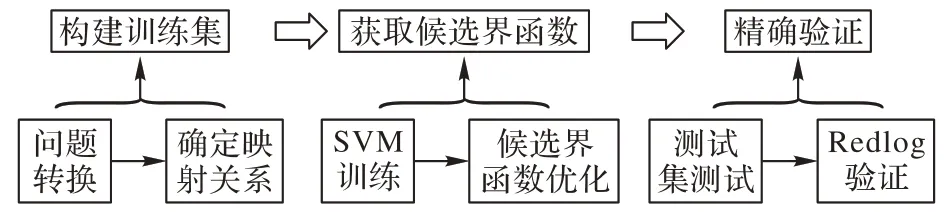
在得到候選的界函數之后，還需要在精確驗證前構造一個測試集對其進行初步的驗證，當所獲得的候選界函數沒能夠通過測試集時，可以將未通過的測試樣本點添加進入訓練集，然后再重新訓練，或者可以通過調整負類點的值，再進行訓練。測試集構造過程如下：本文將上述所得的候選界函數稱為candidate_BF，在循環條件圍成的區域Ω中隨機抽取采樣點若干次。然后針對每一個樣本點代入candidate_BF求解得到該樣本點的迭代次數上界c_cal。最后著代入C(a)求解其真實的迭代次數c_real，若出現c_cal

3 精確驗證

本章將介紹如何對上述所得的候選界函數進行進一步的精確驗證。得到候選界函數之后，并且該函數已經通過測試集驗證，但測試集僅是離散的樣本點，遠遠不能表征整個循環區域Ω，因此，還需要對其進行進一步的精確驗證以保證所得到的候選界函數在整個Ω內滿足界函數的性質。本文采用的方法是：首先找出循環中的不變式，然后通過不變式以及工具Redlog 去驗證所得到的函數是否滿足界函數的性質。

3.1 不變式的構建

構建不變式，首先需要設定不變式的模板，本文不變式的模板與前述提及的界函數模板保持一致。假定不變式為I(a，c)：=MT·V(a)≥c，其中MT=(m1，m2，…，md)為參數，c為程序的計數變量用于計算迭代次數。根據不變式的性質，可得：

能夠同時滿足A、B 兩式的表達式便是該循環的不變式，令A 式中MT以及a*需要滿足的范圍為M0，采用Redlog 工具對B 式進行量詞消去（Quantifier Elimination，QE），消去(a，c)，可以得到不變式模板系數MT需要滿足的范圍M1。其中，a*為初始輸入，本文將其參數化。

3.2 候選界函數的驗證

構建不變式是為了利用不變式來驗證候選界函數，如果該循環存在一個不變式能夠推出候選界函數為真，那么該候選界函數就為真正的界函數。基于此，可得：

采用Redlog 工具對式（14）進行量詞消去，消去(a，c)，可以得到式（14）中MT以及a*需要滿足范圍M2。

綜上：對兩次所得到的MT范圍求交，判斷是否存在一組MT，使其滿足A、B、C 三式。因此，可得：

同樣采用Redlog 工具對式（15）進行量詞消去，消去MT，可以得到滿足式（15）中a*需要滿足的范圍M3。對滿足M3的初始值a*必存在一組MT使得該循環存在一個不變式I(a，c)：=MT·V(a)≥c，該不變式能夠蘊含候選界函數。

因此最終還需要驗證是否對于整個循環區域內的初始點都存在一個不變式，使得該不變式能夠推出候選界函數為真，即驗證是否循環區域Ω都在M3內部。

依然采用Redlog 工具對式（16）進行量詞消去，消去a*，若最終輸出結果為真，那么表示整個循環區域內的點均能夠找到一個與之對應的不變式，并且該不變式能夠蘊含候選界函數。

綜上所述，利用Redlog 工具借助不變式驗證候選界函數的算法如下：

本文在求解候選界函數時并不局限于函數的形式，超越函數、多項式函數均可，但是由于后期驗證依賴于Redlog 工具，而由于Redlog 工具本身的局限性，導致它無法處理一些高次的多項式函數以及超越函數，因此對這類候選界函數Redlog 無法進行驗證，這也是本文循環程序界函數計算方法的局限所在。綜上所述，求解某給定循環其對應的界函數的過程框架如圖1 所示。

圖1 界函數合成框架Fig.1 Framework of synthesizing loop bound function

其中在通過SVM 獲取候選超平面時，由于本文將界函數的計算問題轉化為線性二分類問題，因此在SVM 訓練時均采用線性核函數。此外，并非所有的循環經過一次訓練就可以直接通過測試集，因此當第一次訓練后的候選界函數并未通過測試集時，將測試集中未通過的點重新加入訓練集進行訓練，然后自行設定訓練次數，重復上述過程。整個實驗流程如圖2 所示。

圖2 基于SVM的循環程序界函數計算流程Fig.2 Flowchart of calculating loop bound function for loop program via SVM

綜上所述，算法5 描述了對于給定循環程序，其界函數計算過程如下：首先設定界函數的模板從而得到映射關系，然后調用算法2 構建訓練集，得到訓練集利用SVM 進行訓練得到分類超平面進而得到候選的界函數，再對該候選界函數進行優化得到新的候選界函數，之后通過算法3 利用測試集對該候選界函數進行初步驗證，最后利用算法4 對通過測試集驗證的候選界函數利用Redlog 工具進行精確驗證，如果驗證通過，那么該候選界函數便是該循環程序的真正的界函數。

4 實驗與結果分析

本文求解候選界函數是通過Python 利用Scikit-learn［28］包進行實現，并且所有的實驗均基于2.9 GHz Intel Core i5-9400f CPU 和8 GB 2 666 MHz DDR4 RAM 的PC 上進行的。

4.1 實驗結果

所有循環均取自于兩種方式：一是現有其他文獻工作中的循環；二是在現有文獻工作中的循環基礎上進行了修改。表1 列出了本次實驗所涉及的循環，其中循環1～2 來自于界函數相關文獻［21-22］中所提及的循環，循環3～6 來自于秩函數相關文獻［17］中的循環，循環7～9 則是對秩函數相關文獻中循環基礎上作出了修改，循環10 則是取自于文獻［12］。

表1 實驗所涉及的循環Tab.1 Loops for experiments

從表2 可以看出：不同的循環有著各自不同的模板，并且不同的循環其所選取的負類點的值也各不相同。此外，還可以看出，針對從界函數文獻中提取的循環1～2，本文方法能夠獲得該循環所對應的界函數；針對從秩函數文獻中獲得的循環3～6，本文方法能夠對這些循環求解其對應的界函數；針對循環7～9，當前求解秩函數方法不能獲取其線性秩函數，只能夠求解其多階段線性秩函數，但是本文方法卻能夠獲得其全局的線性界函數；針對循環10，對比方法不能得到其線性秩函數以及多階段線性秩函數，本文方法也能獲得其對應的界函數。

表2 實驗參數以及所得模板系數Tab.2 Experimental parameters and template coefficients

4.2 實驗對比

對于上述10 個循環將本文方法與當前循環程序終止性驗證的主流方法秩函數法作出對比以及與界函數相關方法作出比較。

4.2.1 與秩函數法的對比

秩函數是程序終止性驗證的主流方法，因此首先選取了三種當前合成秩函數的方法與本文方法在可行性以及合成秩函數或者界函數形式這兩個方面作出對比。表3 描述了針對表1 的循環程序，基于量詞消去秩函數合成、基于SVM秩函數合成以及多階段秩函數合成方法與本文方法的實驗結果。

從表3 的實驗結果可以看出：

表3 不同方法的可行性對比Tab.3 Feasibility comparison of different methods

1）基于QE 的方法由于其運算復雜度高，因此一般用于處理線性循環，無法處理多階的循環程序，而本文方法可以處理多階的循環程序。

2）基于SVM 的秩函數合成方法其本身需要設定秩函數模板，再求解模板系數的值，因此對于一些存在多階段秩函數的循環程序便無法合成，而本文界函數方法可以合成全局的界函數。

3）基于線性規劃的多階段線性秩函數合成，它本身只能針對單路徑線性約束循環程序，對于一些二次或高次的循環程序便不能合成對應的秩函數。

綜上所述，針對表1 所述的循環程序，在可行性上，本文方法能夠處理更多的循環。接下來將上述三種秩函數所能得到的秩函數形式與本文方法所能得到的界函數形式進行對比，表4 羅列了針對表1 的循環，秩函數方法所能合成的秩函數形式以及本文方法所能得到的界函數形式。

表4 實驗所得函數形式結果對比Tab.4 Comparison of experimental results in functional forms

從表4 可以看出，與三種秩函數的合成方法所求解得到的秩函數形式相比，本文方法求解得到的界函數在形式上更加簡潔并且所得到的界函數均為全局界函數。

1）針對循環5～6，基于SVM 的方法雖然能夠得到秩函數，但是秩函數形式是非線性的，而本文方法卻能夠求解得到其所對應的線性界函數，相較于非線性模板，線性模板在模板的選取上更加簡潔直接。

2）針對循環7～9，此類循環沒有線性秩函數，僅僅存在多階段線性秩函數。本次實驗多階段秩函數的求解過程采用了irankfinder 工具進行實驗，并將本文方法與文獻［12］中的求解多階段線性秩函數合成法進行對比，從表4 結果可以看出，文獻［12］方法無法求解得到該循環所對應的全局線性秩函數，僅僅能夠獲得多階段的線性秩函數，但是本文方法卻可以得到全局的線性界函數。

3）針對循環10，該循環利用秩函數求解方法，無法獲取其線性秩函數以及多階段線性秩函數，但是本文方法卻能夠求解其非線性的界函數。此外，實驗中設置了簡單的模板嘗試求解循環12 的2 次秩函數，但通過計算發現沒有相應的秩函數（倘若設置復雜的2 次模板，則超出了工具的計算能力）。

綜上所述，針對表1 所述的循環程序，與當前的三種秩函數的合成方法相比較，本文界函數方法不僅能夠處理更多的循環，并且還有著以下的特點：一是對某些循環，秩函數法僅能夠獲取非線性的秩函數，但是本文界函數法能夠獲取線性的界函數，相較于非線性結構，線性結構更為簡潔；二是對某些循環，秩函數法僅僅能夠求解多階段的線性秩函數，但是本文界函數法能夠得到全局的界函數；三是對某些循環，秩函數方法無法求解得到其對應的線性秩函數或者多階段線性秩函數，但是本文方法能夠獲得其非線性的界函數。

4.2.2 與界函數法的對比

相較于現有界函數求解方法，本文提出了一個新的界函數求解思路，即將界函數的求解問題轉化為線性的二分類問題，然后利用SVM 得到分類超平面進而求解得到模板系數。因此本文方法求解候選界函數的過程并不局限于循環程序的形式，循環程序可以是多項式或者非多項式。此外，對于候選界函數的證明過程，本文給出了一個更加具有完備性的驗證過程：

1）文獻［18-19，22］中的方法所針對的循環并非將初始值全部作為參數，而是給定具體的初始值或者給定部分初始值；本文方法所針對的循環程序是將初始值作為參數的循環。

2）文獻［21］方法在驗證候選界函數時也需要獲取不變式，該方法首先將不變式的求解轉化為二次規劃優化問題，再利用現有求解器獲取候選的不變式，最后驗證該候選不變式是否為真正的不變式；而本文方法則是利用符號計算，在不變式參數全空間對滿足條件的不變式進行查找，因此相較于文獻［21］方法，本文方法更加完備。例如：針對循環1，文獻［21］方法需要首先求解得到候選的不變式為a1+a2-≥c，然后再驗證該不變式是否為真正的不變式，而與之不同的是本文方法采用符號計算在不變式參數全空間去尋找滿足條件的不變式，因此并不需要求解得到具體的不變式，僅需考慮其存在性。

5 結語

本文將界函數的求解問題轉化為線性二分類問題，提出了一個新的方法去尋找循環程序的界函數。首先，設定一個界函數模板，然后利用SVM 查找分類超平面獲取模板系數從而得到候選的界函數，最后通過現有符號驗證工具Redlog結合不變式精確驗證其是否是一個正確的界函數。從實驗結果可以看出，相較于當前的秩函數相關方法，針對循環5～6，秩函數方法只能夠找到其非線性的秩函數，但本文方法能夠得到其對應的線性界函數；針對循環7～9，該循環沒有對應的線性秩函數，只有多階段線性秩函數，但是本文方法能夠得到其對應的全局線性界函數；針對循環10，當前秩函數方法不能得到其對應的線性秩函數以及多階段線性秩函數，而本文方法能夠得到其對應2 次界函數。但是，后期的驗證過程仍然依賴于Redlog 工具，因此對于一些循環利用本文方法即使能夠獲得其候選的界函數，但是由于Redlog 工具計算能力的局限性，不能對其進行驗證。此外，如何更加有效率地選取界函數模板以及訓練集中的負類點也是在未來工作中需要進一步深入研究的問題。