A*初始化的變異灰狼優(yōu)化的無人機(jī)路徑規(guī)劃

曹建秋，張廣言，徐 鵬

重慶交通大學(xué) 信息科學(xué)與工程學(xué)院，重慶400074

無人飛行技術(shù)是當(dāng)前很多領(lǐng)域的重要研究內(nèi)容之一[1]，其中包括地形勘測(cè)[2]、無人運(yùn)輸、民用無人機(jī)[3]等。路徑規(guī)劃是無人機(jī)任務(wù)規(guī)劃中最重要的一部分，它需要在一定的約束條件下，獲取自起始點(diǎn)到目標(biāo)點(diǎn)的安全、快速和最小消耗的路徑[4-5]。通過建立模型，可將路徑規(guī)劃問題看作一個(gè)復(fù)雜的優(yōu)化問題，需要高效的算法來進(jìn)行求解。

近年來，各種智能算法相繼提出并應(yīng)用在路徑規(guī)劃問題上，其中包括粒子群算法（particle swarm optimization，PSO）[6]、遺傳算法（genetic algorithm，GA）[7]等，隨著問題復(fù)雜度的增加，傳統(tǒng)群智能算法往往產(chǎn)生過快陷入局部最優(yōu)解、迭代過慢等問題[8]。在此基礎(chǔ)上，一些針對(duì)群智能算法進(jìn)行改進(jìn)的算法相繼被提出，較為有效地解決了上述問題。

灰狼優(yōu)化（gray wolf optimazer，GWO）算法是一種新興的群智能元啟發(fā)式算法，其在2014年被Mirjalili提出。此算法借鑒了灰狼的社會(huì)組織與狩獵時(shí)的行為模式，具有很強(qiáng)的探索能力[9-10]。與其他元啟發(fā)式算法相比，灰狼優(yōu)化具有不需要計(jì)算梯度、算法靈活簡單、便于實(shí)現(xiàn)等優(yōu)點(diǎn)。作為一種高效的優(yōu)化算法，灰狼優(yōu)化被大量應(yīng)用在許多工程應(yīng)用問題[11-12]。但與之前的群智能算法相同，灰狼算法同樣具有與前文算法類似的問題，為解決這一問題，現(xiàn)有的對(duì)于灰狼優(yōu)化算法的改進(jìn)主要體現(xiàn)在三方面：第一，引入非線性慣性權(quán)重以及自適應(yīng)交叉編譯策略，如李靖等人[13]通過引入余弦收斂因子加快狼群在找到獵物后的攻擊速度，即迭代后期的收斂速度，袁光輝[14]通過使用具有正弦曲線特性的慣性權(quán)重提升搜索能力與尋優(yōu)精度，并引入了自適應(yīng)交叉編譯策略，使得適應(yīng)度較低的個(gè)體通過變異避免算法后期陷入局部最優(yōu)；第二，引入路徑微調(diào)算子，如劉二輝等人[15]在其改進(jìn)的灰狼優(yōu)化算法中引入了按照情景設(shè)定的路徑微調(diào)算子和鄰域變異算子，提高了算法的局部開發(fā)能力，避免算法迭代到后期的進(jìn)化停滯；第三，引入新的初始解生成算法，文獻(xiàn)[15]同樣使用了一種自定義的啟發(fā)式規(guī)則生成初始解，提升了初始種群的數(shù)量，進(jìn)而提高了算法穩(wěn)定性。

為了提高路徑規(guī)劃問題的收斂速度，結(jié)合不同元啟發(fā)式算法的全局或局部搜索能力，提出一種基于A*初始化的變異灰狼優(yōu)化算法（A* initialized mutable gray wolf optimazer，AMGWO）。該算法可快速計(jì)算無人機(jī)的最優(yōu)路徑，然后通過三次B樣條曲線進(jìn)行路徑平滑。

1 基礎(chǔ)原理和方法

1.1 無人機(jī)路徑規(guī)劃的數(shù)學(xué)模型

建立分階段求取最優(yōu)節(jié)點(diǎn)的地圖模型，其二維表示如圖1 所示。其中，Pstart與Pend分別代表無人機(jī)路徑的初始點(diǎn)和目標(biāo)點(diǎn)，通過兩點(diǎn)連線構(gòu)建搜索空間的x、y、z坐標(biāo)軸。將搜索空間按列分為N個(gè)階段，圖中Li為階段所在的直線，通過在每個(gè)階段上選取點(diǎn){P1,P2,…,Pn}來生成最終的路徑。threati代表第i個(gè)威脅源，其半徑表示為ri。當(dāng)路徑落入威脅區(qū)時(shí)，無人機(jī)將受到來自地面攻擊設(shè)施、障礙物或其他飛行器的阻擋。故引入代價(jià)函數(shù)，如下節(jié)所述。

圖1 威脅模型Fig.1 Threaten model

1.2 代價(jià)函數(shù)

代價(jià)分為燃料代價(jià)和威脅代價(jià)，假設(shè)無人機(jī)保持勻速航行，則到達(dá)階段Lk時(shí)的燃料代價(jià)退化為路徑長度[16]：

式中：li代表了階段Li-1與階段Li之間的所選路徑線段（簡稱線段）長度。

為簡化問題復(fù)雜度，提出一種威脅代價(jià)函數(shù)，其通過路徑線段與威脅源和威脅邊界兩者的距離來確定，當(dāng)路徑某段線段落入威脅區(qū)時(shí)，線段距離威脅源越近，威脅代價(jià)越大，反之越小，但不會(huì)低于0，函數(shù)表達(dá)如下式：

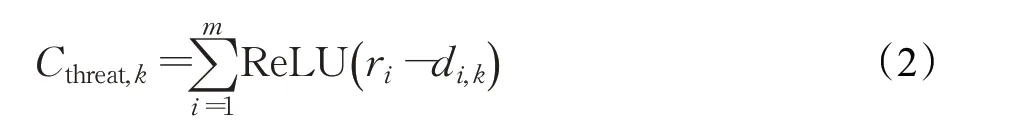
式中：ri代表第i個(gè)威脅源的半徑，di,k代表第k段線段與威脅源的最短距離。ReLU函數(shù)的圖像如圖2所示。

圖2 ReLU函數(shù)的圖像Fig.2 Graph of ReLU

綜上，階段Lk上的總代價(jià)為：

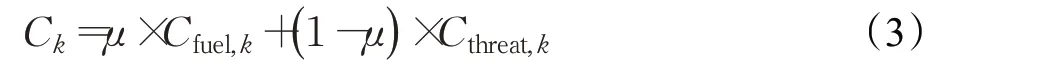
1.3 A*算法

A*算法是一種靜態(tài)路網(wǎng)中求解最短路徑最有效的直接搜索方法，也是許多其他問題的常用啟發(fā)式算法。其能夠在具有任意形狀的威脅和各種約束下進(jìn)行路徑規(guī)劃[17]。作為一種搜索算法，A*可以提供一種較優(yōu)的可行解，使得在其基礎(chǔ)上迭代的算法擁有一個(gè)較優(yōu)的起點(diǎn)。

A*算法的代價(jià)公式表示為：

式中：f(n)是經(jīng)由狀態(tài)n的整體代價(jià)估計(jì)；g(n)是從初始狀態(tài)到狀態(tài)n的實(shí)際代價(jià)；h(n)是從狀態(tài)n到目標(biāo)狀態(tài)的估計(jì)代價(jià)。

1.4 灰狼優(yōu)化

灰狼優(yōu)化算法是一種新的元啟發(fā)式算法，現(xiàn)已被用在路徑規(guī)劃問題上，成為一種有效的路徑規(guī)劃算法[18]。

1.4.1 灰狼優(yōu)化更新過程

灰狼優(yōu)化算法的優(yōu)化模式具有較強(qiáng)的開發(fā)能力，并且由于其不需要計(jì)算梯度的特性，使得該算法運(yùn)行速度快，迭代之間的種群變化較大，可以成為較為有效的進(jìn)化框架為后續(xù)局部開發(fā)算法提供配合。

灰狼優(yōu)化通過以下公式更新狼群：

式中：t指當(dāng)前迭代，Xi代表第i個(gè)個(gè)體在搜索空間中的位置，Xp是目標(biāo)的位置，系數(shù)向量A和C表示為：

式中：r0,1代表在（0，1）之間隨機(jī)取一個(gè)值，不同式中的r0,1不相等。a是一個(gè)隨著迭代從2到0線性減小的值。

標(biāo)準(zhǔn)灰狼算法中，狼群適應(yīng)度前三的個(gè)體被稱作頭狼，分別定義為α、β和γ，其余的個(gè)體為ω。實(shí)際搜索過程使用以下公式進(jìn)行更新：

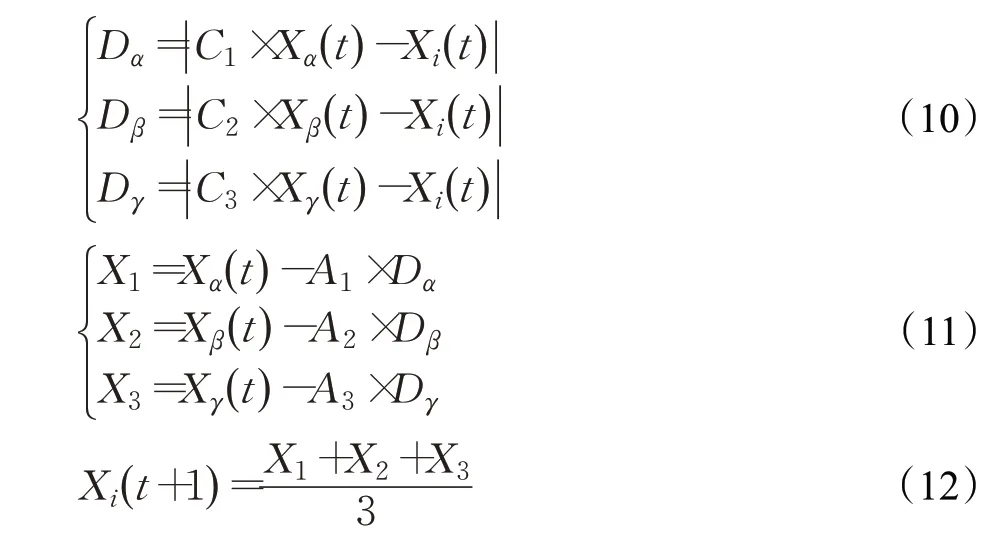
每次更新完畢后，從群體中重新選舉頭狼。

1.4.2 灰狼優(yōu)化的收斂性

收斂性是評(píng)價(jià)一個(gè)算法是否可以收斂到全局最優(yōu)解的指標(biāo)，其通過數(shù)學(xué)方法對(duì)算法進(jìn)行收斂性分析，進(jìn)而證明算法的有效性[19]。馬駿等人通過馬爾可夫過程相關(guān)理論給出了標(biāo)準(zhǔn)灰狼優(yōu)化的收斂性分析，證實(shí)了灰狼優(yōu)化的概率矩陣存在全局最優(yōu)解，且收斂概率為1[20]。

1.5 B樣條路徑平滑

在無人機(jī)實(shí)際飛行作業(yè)中，機(jī)器硬件本身具有各種性能限制，例如最小轉(zhuǎn)彎半徑、最大加速度等約束。為避免飛行器出現(xiàn)瞬間轉(zhuǎn)彎或路徑曲率變化超過性能限制的問題，AMGWO 算法采用B 樣條曲線進(jìn)行路徑平滑，其曲線如圖3所示。

圖3 B樣條曲線Fig.3 B-spline curve

2 A*初始化的變異灰狼優(yōu)化算法

AMGWO算法的前半部分結(jié)合了A*算法和灰狼優(yōu)化的優(yōu)點(diǎn)來解決全局有效搜索的問題，通過對(duì)A*算法在離散化的低精確度地圖上求取結(jié)果，以向灰狼算法提供一個(gè)適應(yīng)度較高的初始頭狼。通過灰狼優(yōu)化的全局搜索能力保證對(duì)搜索空間的探索能力。

AMGWO 算法的后半部分使用了修正變異算子對(duì)狼群個(gè)體進(jìn)行變異，以增強(qiáng)狼群的局部搜索能力。此變異算子是針對(duì)路徑規(guī)劃問題而提出的修正變異算子。

2.1 AMGWO算法

2.1.1 初始化

AMGWO算法種群初始化過程包含頭狼的A*初始化與狼群的隨機(jī)初始化兩個(gè)步驟，頭狼與隨機(jī)生成的狼群數(shù)量總和為設(shè)定的種群個(gè)體數(shù)。

對(duì)于通過迭代方式進(jìn)行優(yōu)化的群智能優(yōu)化算法，一個(gè)較優(yōu)的起點(diǎn)可以指引群體在迭代前期的移動(dòng)方向，減少算法在迭代前期由于頭狼適應(yīng)度過低導(dǎo)致收斂不明顯，并加快其整體的收斂速度，減少達(dá)到理想最優(yōu)值的時(shí)間。

本文使用A*算法進(jìn)行頭狼的初始化，由于算法具有離散性，不能對(duì)連續(xù)化open區(qū)間求啟發(fā)式函數(shù)，通過在每一階段上均勻選取n個(gè)點(diǎn)加入open區(qū)間進(jìn)行前向搜索，保證了搜索范圍，同時(shí)又簡化了open區(qū)間。此時(shí)算法只能得到可行解，不能得到最優(yōu)解，故需要結(jié)合后續(xù)算法進(jìn)行優(yōu)化。為了加快迭代速度，且降低過快陷入局部最優(yōu)的概率，將頭狼簡化為一只[6]。

此時(shí)，A*的代價(jià)函數(shù)f(k)可由下式表示：

狼群的初始化采用隨機(jī)選取每階段節(jié)點(diǎn)的方式進(jìn)行，此時(shí)只能找到無威脅約束域下的可行解。

2.1.2 通過灰狼優(yōu)化更新狼群

頭狼僅一只時(shí)的狼群更新公式如下：

將參數(shù)a設(shè)為1，使狼群全局搜索能力不隨迭代下降。

2.1.3 修正變異

為提高種群質(zhì)量，提出一種路徑微調(diào)算子，其針對(duì)路徑規(guī)劃問題中產(chǎn)生的解使用了隨機(jī)變異的方式進(jìn)行微調(diào)，稱其為修正變異算子。此方法通過隨機(jī)修正個(gè)別路徑點(diǎn)使其落在前后點(diǎn)所在直線上，從而優(yōu)化路徑。對(duì)于路徑規(guī)劃問題，一個(gè)n維的個(gè)體中，第k個(gè)維度上的值與其前后兩個(gè)維度上的值緊密相關(guān)（兩點(diǎn)之間直線最短）：

式中：ik,amend是個(gè)體Xi上第k維的值被前后值修正后的值。而使用這一新值的個(gè)體被稱作Xi,amend，將其與原值進(jìn)行對(duì)比。新的個(gè)體生成按照下式：

同隨機(jī)變異一樣采取擇優(yōu)保留策略的修正變異算子增強(qiáng)了算法的收斂性，經(jīng)過修正變異后的個(gè)體代價(jià)將不會(huì)升高。此步可設(shè)定執(zhí)行概率來加快整體優(yōu)化速度。

2.2 搜索步驟

如圖4所示，AMGWO主要分為兩步：

步驟1初始化。首先用A*算法初始化頭狼，并且隨機(jī)生成最大種群數(shù)量減一的狼群，隨后將頭狼置入狼群。

步驟2更新迭代。開始種群迭代后，每一次迭代過程中，首先使用式（14）對(duì)狼群進(jìn)行位置更新，隨后隨機(jī)選取一部分狼，通過式（16）、（17）對(duì)它們進(jìn)行修正變異。當(dāng)?shù)螖?shù)達(dá)到設(shè)定值后結(jié)束迭代并返回結(jié)果。

2.3 算法性能分析

2.3.1 計(jì)算復(fù)雜度

如圖4 所述，AMGWO 算法共可分為三大部分：步驟1初始化在算法開始執(zhí)行時(shí)僅執(zhí)行一次，其中包含A*算法和種群初始化。步驟2為灰狼優(yōu)化算法更新群體，步驟3為修正變異，此兩步在迭代中反復(fù)執(zhí)行。對(duì)于一個(gè)包含N個(gè)個(gè)體，每個(gè)個(gè)體表示為一個(gè)D維向量的種群來說：

圖4 AMGWO的算法流程Fig.4 Algorithm flow of AMGWO

步驟1初始化。A*算法使用離散的模型，通常將連續(xù)化模型離散為包含D×Dy個(gè)點(diǎn)的網(wǎng)格地圖，由于其帶有有向性，并且open表總是下一階段的全體節(jié)點(diǎn)，故復(fù)雜度為O(D×Dy)，通常情況下Dy為較小的有限值（一般取6到10），故其復(fù)雜度應(yīng)為O(D)。種群初始化涉及到N個(gè)D維向量的隨機(jī)初始化。此階段的計(jì)算復(fù)雜度為O(N×D)。

步驟2GWO 的更新。通過種群最優(yōu)個(gè)體的影響，GWO 將每個(gè)個(gè)體更新為一個(gè)新的個(gè)體，其中不涉及其他運(yùn)算，故此階段的復(fù)雜度應(yīng)為O(N×D)。

步驟3修正變異。隨機(jī)選取個(gè)體向量上的某個(gè)維度，通過相鄰維度的值的影響重新分配其值來更新個(gè)體，此階段的復(fù)雜度為O(N×D)。

額外步：代價(jià)的計(jì)算。計(jì)算路徑上每個(gè)線段與全部威脅間的威脅代價(jià)，即點(diǎn)到線段的距離，若威脅區(qū)數(shù)量為T，則此步的復(fù)雜度為O(D×T)。

綜上所述，算法的時(shí)間復(fù)雜度為O(N×D×T)，已知N、D、T皆為有限常數(shù)，則證明該算法具有最快級(jí)別的速度。

2.3.2 收斂性分析

由前文所述可知，AMGWO在簡化的灰狼優(yōu)化過程中使用了精英保留策略，故增強(qiáng)了算法較原GWO 算法的收斂性[21-22]。同樣的，在修正變異算子中，使用了擇優(yōu)保留的策略，同樣可使算法概率矩陣存在一個(gè)全局最優(yōu)，并且收斂概率為1。

3 仿真實(shí)驗(yàn)

為說明AMGWO 相比于其他算法的優(yōu)越性，設(shè)計(jì)了3 個(gè)仿真案例（分為二維環(huán)境和三維環(huán)境，二維環(huán)境指表中去除第3個(gè)維度的環(huán)境）來對(duì)AMGWO算法的性能進(jìn)行評(píng)估，具體案例參數(shù)如表1所示。

表1 3個(gè)案例的各項(xiàng)參數(shù)Table 1 Parameters of 3 cases

起點(diǎn)與終點(diǎn)分別設(shè)定為搜索空間的左邊界和右邊界中點(diǎn)。最大迭代次數(shù)為100，種群個(gè)數(shù)設(shè)定為50，μ為0.5。對(duì)3個(gè)仿真案例分別使用AMGWO、PSO、GWO、SOS[23]進(jìn)行10次獨(dú)立搜索，記錄各算法收斂速度以及統(tǒng)計(jì)結(jié)果。

本實(shí)驗(yàn)使用一臺(tái)CPU 為AMD R5 3500H 的筆記本電腦，程序使用Python 3.7于PyCharm中編寫。

3.1 修正變異概率的參數(shù)分析

為確定修正變異概率Pamend的最優(yōu)取值，取二維環(huán)境的第一個(gè)案例，在步長為0.01的情況下，將Pamend自0取至1，分別執(zhí)行路徑規(guī)劃。

在圖5（a）中，當(dāng)本文提出的算法（AMGWO）不使用修正變異算子(Pamend=0)時(shí)，其規(guī)劃代價(jià)較于使用修正變異算子(0

圖5 參數(shù)隨變異概率Pamend 的變化Fig.5 Variation of parameters with Pamend

3.2 二維環(huán)境規(guī)劃

對(duì)于第一個(gè)案例，圖6（a）展示了5 個(gè)算法（包含用于初始化的A*算法）的實(shí)驗(yàn)結(jié)果以及差異對(duì)比。圖中可見，4 個(gè)算法均獲得了可行解，其中本文提出的算法（AMGWO）表現(xiàn)雖好，其規(guī)劃出的曲線減少了絕大部分不必要的彎曲，并且滿足B 樣條曲線的定義，意味著曲線滿足無人機(jī)的轉(zhuǎn)彎性能要求。其余3 個(gè)算法得到了可行解，但不是最優(yōu)，并且在曲線中可以看到不必要的彎曲。

圖6（b）展示了4 個(gè)算法的代價(jià)收斂曲線。可以看出，在A*算法的初始化下，AMGWO的代價(jià)收斂起點(diǎn)大大低于其他算法，隨著迭代，收斂效果較好。GWO算法雖然收斂速度較快，但在約40 次迭代時(shí)進(jìn)入了局部最優(yōu)，后續(xù)未能跳出。PSO效果略好于GWO，但同樣收斂到了局部最優(yōu)。SOS隨著迭代進(jìn)行整體呈下降趨勢(shì)，但收斂速度較慢，并且在局部最優(yōu)停留時(shí)間略長。

圖6（c）展示了4 個(gè)算法分別在10 次獨(dú)立執(zhí)行結(jié)果中的最優(yōu)值、平均值和最差值。首先可以看出，AMGWO算法在10 次執(zhí)行中均得到了收斂較好的解，這意味著該算法具有良好的穩(wěn)定性。而對(duì)于其他算法，在平均值和最差值上均有不同程度的升高，其中SOS變化幅度最大，這表明了其他算法具有較差的穩(wěn)定性，不可用于實(shí)際飛行。

圖6 二維案例1的運(yùn)行結(jié)果與統(tǒng)計(jì)Fig.6 Optimization results and statistics of 2D Case1

在第二個(gè)案例中，增加了威脅源擺放的復(fù)雜度，從圖7（a）可看出，AMGWO仍然搜索到了最優(yōu)路徑。PSO的結(jié)果最接近AMGWO，但相比之下其曲線包含了多余的彎曲。GWO 和SOS 得到的路徑是失敗的，它們均穿過了威脅區(qū)，從圖7（b）中的收斂曲線可看出，GWO收斂速度較快，其在最快的時(shí)間里得到了除AMGWO 的結(jié)果之外的最優(yōu)解，但結(jié)合路徑曲線可知，其結(jié)果是失敗的。而AMGWO有著最好的代價(jià)收斂曲線和結(jié)果。圖7（c）同樣展示了算法的穩(wěn)定性差異，其中AMGWO 算法最為穩(wěn)定。而另外三者有著較差的穩(wěn)定性，其中PSO 較好，另外兩者較差。在第三個(gè)案例中，將威脅區(qū)簡化為兩個(gè)，如圖8 所示，在100 次迭代后，AMGWO 找到了最優(yōu)解，PSO 與GWO 的規(guī)劃結(jié)果較AMGWO 相差不大，但出現(xiàn)了不必要的彎曲路徑。收斂曲線與統(tǒng)計(jì)結(jié)果與前兩個(gè)案例相似，依然表現(xiàn)出了前文所述的代價(jià)收斂特征和穩(wěn)定性差異。四種算法的統(tǒng)計(jì)結(jié)果見表3。

圖7 二維案例2的運(yùn)行結(jié)果與統(tǒng)計(jì)Fig.7 Optimization results and statistics of 2D Case2

圖8 二維案例3的運(yùn)行結(jié)果與統(tǒng)計(jì)Fig.8 Optimization results and statistics of 2D Case3

3.3 三維環(huán)境規(guī)劃

三維環(huán)境通過增加階段上節(jié)點(diǎn)維度來增加問題復(fù)雜度，但算法本質(zhì)相同。圖9（a）展示了三維環(huán)境中各個(gè)算法的最終規(guī)劃路徑，在增加了問題復(fù)雜度的情況下，AMGWO 算法的結(jié)果仍然保持了最優(yōu)，沒有多余的彎曲，而其余算法均有了更大程度的彎曲。這得益于其所使用的修正變異算子，其對(duì)路徑規(guī)劃問題做了針對(duì)性優(yōu)化。圖9（b）展示了四種算法的收斂曲線，在三維環(huán)境中，GWO 的表現(xiàn)較二維有較大幅度的惡化，而SOS 和PSO保持了正常的收斂速度，這說明了對(duì)于高復(fù)雜度的問題，AMGWO算法仍然保持了高性能。在圖9（c）中，四種算法的表現(xiàn)與前文相似，均表現(xiàn)了前文描述中各自的穩(wěn)定性。

圖9 三維案例1的運(yùn)行結(jié)果與統(tǒng)計(jì)Fig.9 Optimization results and statistics of 3D Case1

在圖10中，與二維環(huán)境相同，圖（a）中威脅區(qū)的半徑增大，擺放復(fù)雜度也有了提升，在這種環(huán)境下，AMGWO在所得結(jié)果、收斂曲線和統(tǒng)計(jì)結(jié)果所表現(xiàn)的穩(wěn)定性方面均有較高程度的領(lǐng)先。

圖10 三維案例2的運(yùn)行結(jié)果與統(tǒng)計(jì)Fig.10 Optimization results and statistics of 3D Case2

圖11展示了大威脅半徑與減少威脅區(qū)個(gè)數(shù)的環(huán)境下四種算法的表現(xiàn)，除AMGWO 算法的結(jié)果仍保持較好的領(lǐng)先外，其余算法的效果較差。具體表現(xiàn)為沒有減少不必要的彎曲，收斂速度過慢且最終結(jié)果較差，統(tǒng)計(jì)結(jié)果也表現(xiàn)了它們的穩(wěn)定性過低的特點(diǎn)。

圖11 三維案例3的運(yùn)行結(jié)果與統(tǒng)計(jì)Fig.11 Optimization results and statistics of 3D Case3

四種算法的統(tǒng)計(jì)結(jié)果見表2。

表2 四種算法路徑代價(jià)統(tǒng)計(jì)結(jié)果Table 2 Path cost statistics of four algorithms

3.4 規(guī)劃時(shí)間對(duì)比

將各算法迭代100次所消耗的時(shí)間如圖12所示，綜合前文所述，GWO 的速度最快，PSO 次之，但搜索效果較差，往往不能得出最優(yōu)解，甚至可能出現(xiàn)規(guī)劃失敗情形。SOS的效果一般，執(zhí)行慢，迭代也慢，無法滿足無人機(jī)實(shí)用要求。

圖12 規(guī)劃時(shí)間對(duì)比Fig.12 Comparison of planning time

AMGWO 的規(guī)劃時(shí)間略高于PSO 和GWO，但搜索效果最好，結(jié)合前文代價(jià)收斂曲線可看出，AMGWO 的收斂速度較快，通常在10 至40 次迭代中即可尋出一個(gè)較好的全局最優(yōu)解，故該算法具有良好的性能。規(guī)劃時(shí)間統(tǒng)計(jì)結(jié)果見表3。

表3 規(guī)劃時(shí)間統(tǒng)計(jì)Table 3 Planning time statistics s

4 結(jié)束語

針對(duì)帶有威脅源的復(fù)雜區(qū)域無人機(jī)路徑規(guī)劃問題，本文提出了一種A*初始化的變異灰狼優(yōu)化算法，稱為AMGWO算法。該算法使用了A*算法作為初始化種群首領(lǐng)，極大提升了種群的收斂效果，明確了種群搜索的大致方向，避免了盲目搜索。同時(shí)提出了一種新型的修正變異方法，通過個(gè)體上相鄰維度之間的特定關(guān)系，修改個(gè)體的值，達(dá)到優(yōu)化路徑與提升搜索質(zhì)量的效果。隨后闡述了路徑平滑的常用算法優(yōu)缺點(diǎn)。使用三次B 樣條曲線平滑使最終生成的航跡適合無人機(jī)實(shí)際飛行。

在實(shí)驗(yàn)部分，參數(shù)分析表明，修正變異算子有其必要性。實(shí)驗(yàn)結(jié)果分析表明，AMGWO算法能夠獲得一條高效、安全的路徑。并且與其他算法的對(duì)比，也證明了AMGWO 算法在解決無人機(jī)路徑規(guī)劃問題上具有較高的應(yīng)用價(jià)值。