Constitutive modeling of particle reinforced rubber-like materials
Sankalp Gour, Deepak Kumar
Department of Mechanical Engineering, Maulana Azad National Institute of Technology Bhopal, Madhya Pradesh, 462003, India
Keywords:Hyperelastic material Constitutive modeling Strain energy function
ABSTRACT The present study is focused on the constitutive modeling for the mechanical behavior of rubber reinforced with filler particles. A filler-dependent energy density function is proposed with all the continuum mechanics-based necessities of an effective hyperelastic material model. The proposed invariant-based energy function comprises a single set of material parameters for a material subjected to several modes of loading conditions. The model solution agrees well with existing experimental results. Later, the effect of varying concentrations of filler particles in the rubber matrix is also studied.
Rubber or rubber-like materials are made up of soft polymers consisting of a cross-linked molecular chain network. These kinds of materials are often referred to as elastomers [1–5]. These elastomers possess excellent characteristics such as high elastic energy density, high efficiency, large deformation, high responsive speed [6–9]. They have high availability and lower cost. Rubber elastomers have several practical applications, including energy harvesters, braille displays, sensors, manipulators, vibration isolation, and actuators [10,11]. The rubber elastomers have immense potential and are widely adapted for application in medical, robotics, aerospace, and bionics engineering [12–14]. These materials obey the continuum mechanics-based non-linear elasticity approach in which the stress-stretch relation is obtained from thermodynamics-based strain energy potential functions [15–21].In general, a reinforcement of fillers in rubber elastomers improves the mechanical properties of their composites [22]. The improvement can be further enhanced by using the reinforced filler material of higher aspect ratios such as short glass fiber and carbon nanotubes [23–27]. In this regard, Tadiello et al. [28] investigated silica-styrene butadiene rubber (SBR) nanocomposite with spherical and rod-like silica nanoparticles (NPs) synthesized by a sol-gel process aided by a structure guiding agent by varying aspect ratios (AR= 1–5). As a result, dynamic observations indicated that rod-like particles generate stronger rubber reinforcing, increasing aspect ratios. At the sametime, a lot of research focused on the effect of filler and parent rubber interactions to study the influence of the reinforcement on the rubber elastomer.In the past, Wolff et al. [29] studied the interactive nature between carbon black filler and bound rubber with several filler concentrations and tested with different loading conditions. Further,Park et al. [30] performed an experiment based on an interaction between filler-elastomer composite and encountered the growth in cross-link density and thermal stability. Furthermore, Laraba-Abbes et al. [31] investigated the applications of non-linear behaviour characterization of carbon-black reinforced natural rubber elastomer for large deformations and carried out finite element analysis. The current work aims to develop a constitutive model adopting a continuum mechanics-based hyperelastic approach to validate the proposed filler-dependent strain energy density function. The proposed energy function is further used to predict the influence of filler dependency on the composite rubber for uniaxial, equi-biaxial, and pure shearing conditions for varying concentrations of fillers.
In the next, an analytical model is developed to study the influence of filler particles on the mechanical behavior of rubber elastomer under uniaxial, biaxial, and pure shearing deformation conditions. To develop the same, a continuum mechanics-based theory of hyperelasticity is followed. Consider a particle reinforced rubber elastomer sample of dimension (L×L) in undeformed reference configuration as shown in Fig. 1. The sample is considered to be homogeneous, isotropic, and incompressible. The sample is deformed to the current configuration under uniaxial, equibiaxial,and pure shear deformations subjected to mechanical force, as depicted in Fig. 1. We aim here to develop an analytical model to relate the stress and the corresponding deformation following a physics-based continuum mechanics approach.
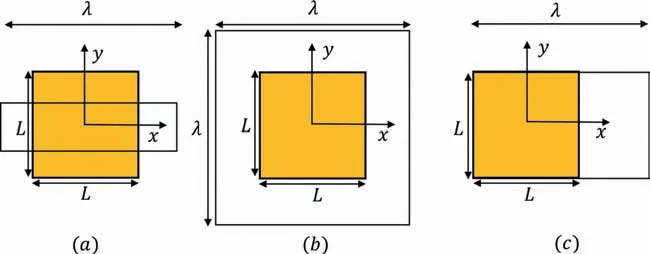
Fig. 1. Deformation conditions:(a) uniaxial tension, (b) equibiaxial tension and (c) pure shearing.
For a given system of configuration, as shown in Fig. 1, the stretches in the principal directions are given by

wherepis a Lagrangian multiplier to impose the incompressibility condition. Further,I1,I2, andI3are the first, second, and third invariants of a deformation gradient tensor B and their expressions in terms of principal stretches corresponding to an incompressible isotropic hyperelastic material class are given by

wherea,b,c, andμare the material parameters andαis a special kind of material parameter accounts for the volume fraction of filler particlesvf. All together, these terms manifest the proposed Exp-ln-ln form of strain energy density function given as

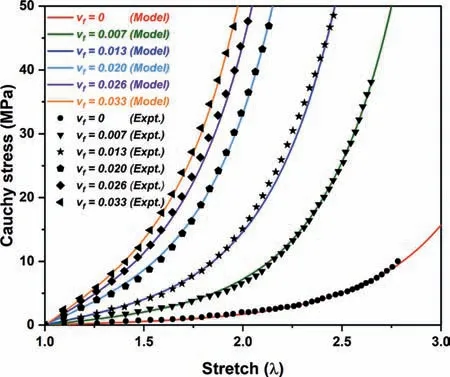
Fig. 2. Parameters identification of the proposed model with uniaxial experimental data [32] of a NBR filled with different volume fraction of CNPs.
We now validate the constitutive model derived from the proposed strain energy function in comparison with the existing experimental data. For this analysis, we fit the material parameters asa=0.27,b=0.18,c=0.058, andμ=0.12 MPa for unfilled rubber(i.e.,vf=0). Next, a set of experimental data performed by Mahmoud et al. [32] for carbon nanoparticles (CNPs) reinforced nitrile butadiene rubber (NBR) data at different volume fractions of CNPs for uniaxial loading conditions is utilized for parameter identification of the model. The comparison between the analytical and experimental [32] results in terms of Cauchy stress versus stretch are plotted in Fig. 2. The volume fraction of CNPs in NBR in line with the experimental data as 0.7%, 1.3%, 2%, 2.6%, and 3.3%, respectively, is considered in line with the experimental [32] to validate the analytical findings of the proposed model (Eq. (7)). Herein,an addition of CNPs to NBR elastomer from 0% to 0.7% encounters a significant rise of 422.2% in the shear modulus of NBR. On further increase in the CNPs content from 0.7% to 1.3%, 1.3% to 2%, 2%to 2.6%, and 2.6% to 3.3% enhances the shear modulus of NBR of 341.67%, 84.90%, 25.75%, and 13.25%, respectively. The experimental results demonstrate that the addition of fillers to the parent elastomer results in a significant increase in the strength of the rubber elastomers. Further, a decreasing tendency of deformation in the parent elastomer is noted with a rise in the concentration of the reinforced filler materials that leads to higher stiffness of the elastomer. This behavior implies that the material is becoming stiffer, which suggests that its deformation capability is also decreasing, because excessive inclusion of filler particles obstructs the free movement of polymeric chains in the parent rubber matrix,causing them to become hard. This phenomenon is often called as the chain stiffening effect in the rubber based polymers [33].
This noted phenomenon may be utilized to eliminate the pullin instability of the rubber elastomers to a certain extent. So, the same elastomer can withstand a higher load without undergoing failure. At last, the material parameters of the model are evaluated by using a well-known least square method of curve fitting[34]. The proposed strain energy function model satisfactorily validates the experiment. The respective shear modulus values of rubber elastomer at different percentages of added CNPs are tabulated inTable 1. A higher shear modulus value is noted in the table for a larger volume fraction of reinforced filler particles. This indicates that the reinforced rubber elastomer acquired a higher value of Cauchy stress for a given stretch value as the filler content increased. However, the model predicts some residual stresses before being subjected to loading conditions.

Table 1 Shear modulus values for a NBR at different percentages of added CNPs.
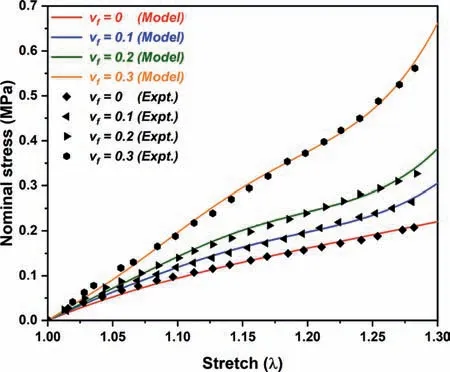
Fig. 3. Parameters identification of the proposed model with biaxial experimental data [35] of an iron particle-reinforced silicone rubber matrix composite..
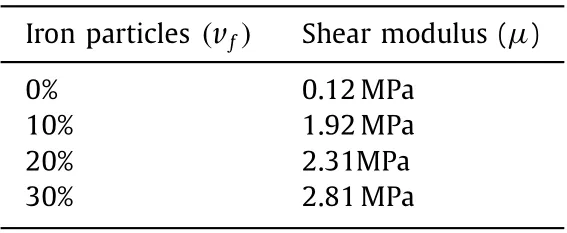
Table 2 Shear modulus values for a silicone rubber at different percentages of added iron particles.
Figure 3 depicts the nominal stress-stretch relationship for equibiaxial deformation model (Eq. (8)) validation from experimental data acquired by Schubert et al. [35] for iron particlereinforced silicone rubber matrix composite.Table 2 lists the shear modulus values of silicone rubber at various percentages of added iron particles in the composite polymer. Figure 4 illustrates the analytical plot of Cauchy stress versus stretch relationship for particle reinforced rubber elastomer under pure shear deformation(Eq. (9)). Herein, the curves are plotted for fixed values of material parameters (i.e.,a=0.27,b=0.18,c=0.058) and varying concentration of filler particles (i.e.,vf) in accordance of Fig. 3 for 0%, 10%,20%, and 30%, respectively. Both Figs. 3 and 4 demonstrate similar kinds of results. We may here observe that with a rise in the reinforcement of filler particles, the Cauchy stress increases for any fixed value of stretch. This suggests that an increase in fillers increases the shear modulus of the polymer. Also, the slope of the curve increases with filler particle content.
In conclusion, the present letter proposed an invariant-based filler-dependent strain energy function that comprises a single set of material parameters for a material subjected to several loading conditions to examine the mechanical behavior of the composite rubber elastomers. A thermodynamics-based classical continuum mechanics approach is followed for deriving the constitutive model. The Cauchy stress response is further obtained from the model and validated with the experimental data. As a result,an enhancement in the shear modulus of the composite elastomer is observed with a rise in the concentration of filler particles. The findings of the current study may be helpful in developing reinforced elastomeric material-based actuators used in rubber manufacturing and soft robotic industries.

Fig. 4. Cauchy stress versus stretch relationship for particle reinforced rubber elastomer in a pure shear deformation condition.
Declaration of Competing InterestThe authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
 Theoretical & Applied Mechanics Letters2022年6期
Theoretical & Applied Mechanics Letters2022年6期
- Theoretical & Applied Mechanics Letters的其它文章
- Generalized boundary dilatation flux on a flexible wall
- Fourier neural operator approach to large eddy simulation of three-dimensional turbulence
- Elastoplastic constitutive modeling under the complex loading driven by GRU and small-amount data
- Numerical simulation of laser ultrasonic detection of the surface microdefects on laser powder bed fusion additive manufactured 316L stainless steel
- Sedimentation motion of sand particles in moving water (I): The resistance on a small sphere moving in non-uniform flow☆,☆☆
- Predicting solutions of the Lotka-Volterra equation using hybrid deep network
