最佳自適應無跡卡爾曼濾波算法應用研究
曹后龍
(上海核工程研究設計院有限公司,上海 200233)
1 引 言
在卡爾曼濾波應用中,狀態方程或量測方程常為非線性函數,則濾波問題也表現為非線性,為了解決在非線性系統中卡爾曼濾波理論的應用問題,S.J.Julier和J.K.Uhlmann提出了無跡卡爾曼濾波[1,2,3],該算法采用線性卡爾曼濾波框架,以無跡變換為基礎,通過某種采樣策略生成采樣點集,然后將采樣點集通過無跡變換得到新的采樣點集,將變換后采樣點集的統計特性作為問題結果,避免了線性化誤差,而且需要很少的采樣點就可以得到優于擴展卡爾曼濾波的估計結果,不僅易于實現而且在保持與線性化方法相當運算量的同時具有較高的估計精度和較廣的適用范圍[4]。
在許多實際問題中,無跡卡爾曼濾波對前一時刻狀態參數估值比較敏感,其誤差將會直接影響濾波的估值;即使前一時刻狀態參數估值合理,由于動力學模型異常誤差的存在,這也會直接影響無跡卡爾曼濾波濾波解的精度[5]。針對上述問題,恰當的自適應因子不僅能夠合理地平衡預測狀態信息與觀測信息之間對濾波估值的貢獻,而且能夠很好地控制前一時刻狀態參數估值誤差與動力學模型異常誤差對濾波估值的影響[6,7,8]。
本文在自適應無跡卡爾曼濾波算法的理論基礎上,給出了其改進算法,引入最佳自適應因子[9],得到最佳自適應無跡卡爾曼濾波。通過最佳自適應因子來調節預測狀態向量的協方差矩陣,即調整預測狀態信息對濾波解更加合理的貢獻,從而進一步提高濾波解的精度。
2 自適應無跡卡爾曼濾波算法
已知tk時刻的狀態方程和觀測方程分別為:
Xk=Φk,k-1Xk-1+wk
(1)
Lk=h(Xk)+ek
(2)
式中,狀態方程為線性函數,觀測方程為非線性函數;Xk為tk時刻的n×1維狀態向量,Φk,k-1為狀態轉移矩陣,Lk為tk時刻m×1維觀測向量,h(Xk)為非線性觀測函數;wk和ek分別為n×1維狀態噪聲向量和m×1維觀測噪聲向量,均為加性高斯白噪聲,兩者的協方差矩陣分別為Qk和Rk,且互不相關。
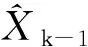
(3)
(4)
(5)
其協方差矩陣和估值為:
(6)
(7)
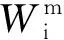
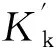
(8)
(9)

(10)
(11)
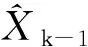
3 最佳自適應因子
在自適應無跡卡爾曼濾波中,恰當的自適應因子不僅能夠合理地平衡預測狀態信息與觀測信息之間對濾波估值的貢獻,而且能夠很好地控制前一時刻狀態參數估值異常誤差與動力學模型異常誤差對濾波估值的影響。
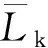
(12)
(13)
(14)
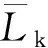
(15)

(16)
則:
(17)
對上式兩端同時取跡可得Ck為:
(18)
(19)

4 算例及分析
在教學樓前廣場進行動態導航定位實驗,車輛載體安裝導航模塊,實驗時長 20 min,接收機采樣間隔T=10s。利用接收機自帶的處理軟件從原始數據文件里導出觀測文件和廣播星歷文件,并對觀測數據和導航數據進行簡單的處理,取觀測數據次數100次。動力學模型采用常速(CV)模型[12,13],觀測模型采用偽距觀測方程[14]。
初始狀態參數估計值X0及其協方差矩陣D0為:
D0=diag(100,100,100,100,0.0012,0.0012,0.0012,1)
狀態噪聲協方差矩陣Q和觀測噪聲協方差矩陣R為:
Q=diag(100,100,100,100,0.0012,0.0012,0.0012,1)
R=diag(100,100,100,100,100,100,100)
使用標準無跡卡爾曼濾波算法和最佳自適應無跡卡爾曼濾波算法分別進行濾波計算比較分析,采樣策略為對稱采樣。
(1)狀預測態信息無異常誤差時,即動力學模型無異常誤差,前一時刻狀態參數估值無異常誤差,如圖1~圖3所示。
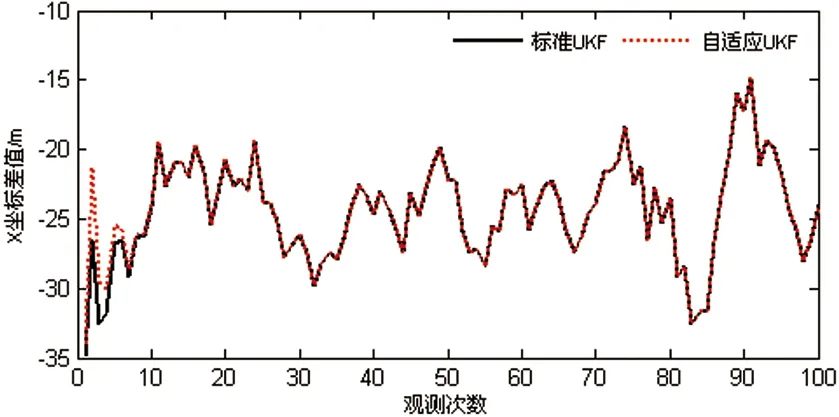
圖1 預測狀態信息無異常誤差時,X坐標差值比較
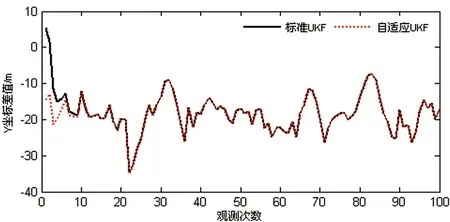
圖2 預測狀態信息無異常誤差時,Y坐標差值比較
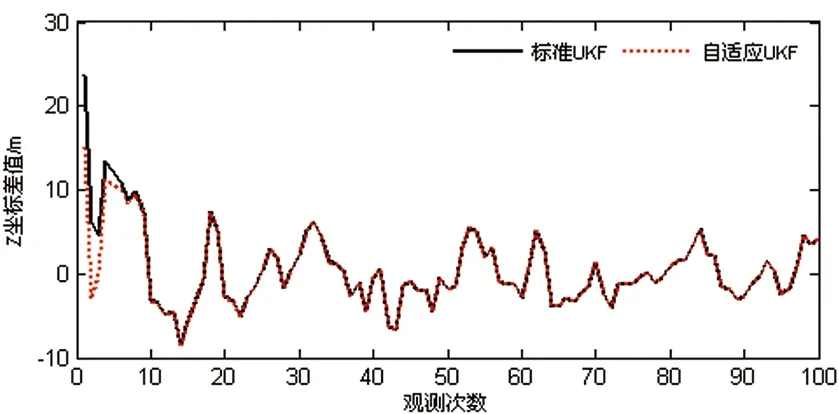
圖3 預測狀態信息無異常誤差時,Z坐標差值比較
(2)在給定初始狀態估值X0不恰當時,即初始狀態參數估值存在較大誤差時,x、y、z坐標差值如圖4~圖6所示。
X0=[-2412100.0 4687600.0 3564900.0 609729.1 0 0 0 100.0]T
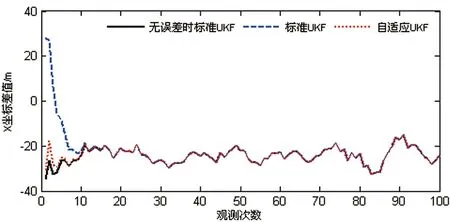
圖4 初始狀態估值有誤差時,X坐標差值比較
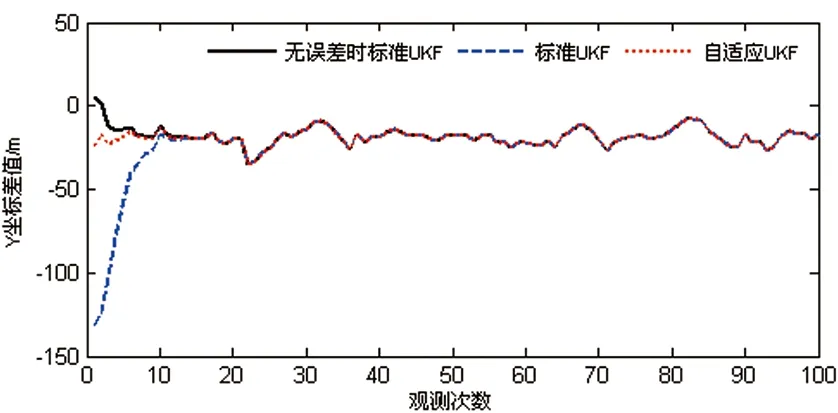
圖5 初始狀態估值有誤差時,Y坐標差值比較
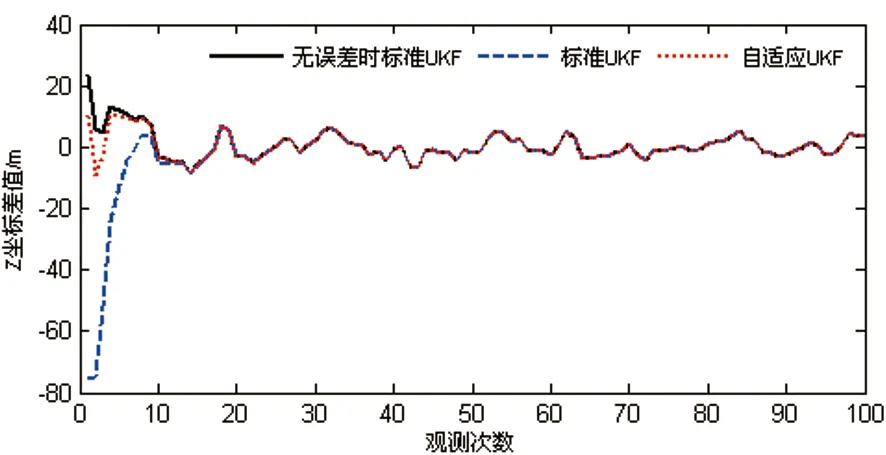
圖6 初始狀態估值有誤差時,Z坐標差值比較
(3)為了檢驗最佳自適應因子的效果,每隔20次就在前一時刻狀態參數估值向量中的X坐標,Y坐標和Z坐標上分別人為地加上 80 m異常誤差,x、y、z坐標差值如圖7~圖9所示,即:

圖7 前一時刻狀態估值有異常誤差時,X坐標差值比較
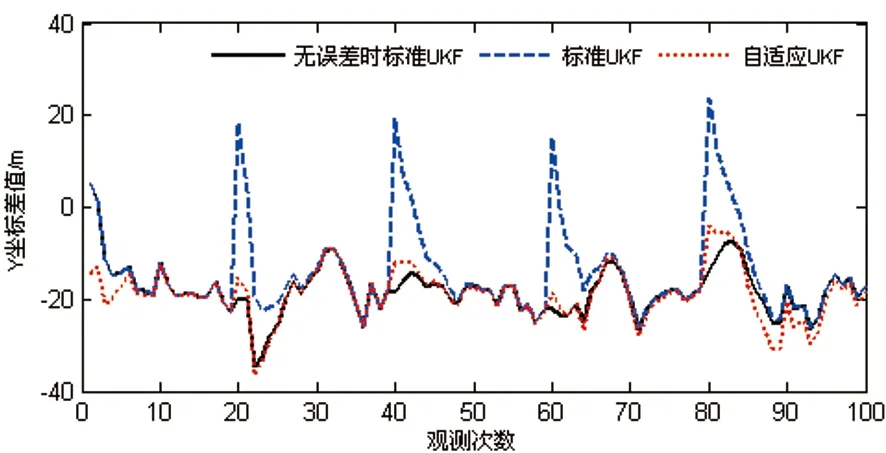
圖8 前一時刻狀態估值有異常誤差時,Y坐標差值比較

圖9 前一時刻狀態估值有異常誤差時,Z坐標差值比較
(1)從圖1、圖2、圖3可以看出,在觀測值可靠的情況下,在濾波初始段,標準無跡卡爾曼濾波估值精度稍微低于最佳自適應無跡卡爾曼濾波估值精度;但在標準無跡卡爾曼濾波算法穩定以后,兩者的濾波結果基本一致,精度相當。
(2)從圖4、圖5、圖6可以看出,在觀測值可靠的情況下,由于狀態參數初始值存在較大誤差,導致了標準無跡卡爾曼濾波初期的濾波結果發散,精度很差,但隨著濾波的進行,逐漸趨于穩定;而最佳自適應無跡卡爾曼濾波通過最佳自適應因子調整初始狀態估值的協方差矩陣,減少初始狀態估值對濾波解的貢獻,得到了可靠的濾波結果,提高了濾波估值的精度。
(3)從圖7、圖8、圖9可以看出,在預測狀態向量存在較大誤差時,標準無跡卡爾曼濾波穩定性很差,得到的濾波結果不可靠;而此時最佳自適應無跡卡爾曼濾波能夠很好地控制預測狀態信息對濾波結果的影響,得到可靠的濾波結果。
5 結 論
本文先給出了自適應無跡卡爾曼濾波算法,再利用預測殘差的理論協方差矩陣與實際協方差矩陣之間的關系,引入無跡卡爾曼濾波中最佳自適應因子,得到了最佳自適應因子無跡卡爾曼濾波算法。當預測殘差實際協方差和理論協方差相等時,即自適應因子Ck=1,此時的自適應無跡卡爾曼濾波就是標準無跡卡爾曼濾波。在觀測值可靠的情況下,預測殘差反映了動力學模型誤差與前一時刻狀態估值誤差總共的大小,最佳自適應無跡卡爾曼濾波將它們作為一個整體,利用最佳自適應因子合理地調整它們整體對濾波結果的貢獻。通過實例驗證了最佳自適應因子在無跡卡爾曼濾波中不僅能夠適用,而且能夠提高濾波結果的精度。

