基于多尺度分析的遙感變化檢測
謝貴臣,何浩,邢棟
(新疆大學建筑工程學院,新疆 烏魯木齊 830047)
1 引 言
遙感變化檢測是遙感影像分析中重要的應用之一,在土地管理、環境監測、農業林業管理、災害救援與治理等領域有廣泛的應用[1]。尺度在遙感影像分析中具有重要意義,在同一景影像中同類地物由于自身大小不同,而無法采用單一分析尺度進行分析。因而最佳分割尺度的確定成為面向對象變化檢測的關鍵問題之一。
針對變化檢測中的尺度問題,蔡怤晟等[2]提出一種結合特征選擇的CVA多尺度遙感影像變化檢測方法,一定程度上提高了變化檢測的準確性。劉紅超等[3]提出一種面向類型特征的自適應閾值遙感影像變化檢測方法,一定程度上減弱物候期對變化檢測的影響,且具有更好的穩定性。徐俊峰等[4]提出一種利用慢特征分析的特征級多尺度融合變化檢測方法,在檢測精度和自動化程度方面更具優勢。王超等[5]結合陰影補償因子,設計了一種基于D-S證據理論的決策級多尺度融合策略,該方法較好地解決了陰影引起的錯檢問題。薛昱晟[6]在地理國情監測中采用了多尺度分割方法,檢測結果優于單一尺度分割的結果。已有的多尺度分割變化檢測方法常將各尺度單獨分析再融合,忽略了尺度間隱含的上下文信息。針對此問題本文提出一種多尺度分析的變化檢測方法。
2 方法
首先,對雙時相影像進行多尺度分割,將前后時相的分割結果疊置,生成子對象;其次,以大、中、小尺度下的子對象為基本分析單元,計算影像光譜特征的結構相似性測度,得到某一尺度下子對象的變化強度圖;最后,對各尺度下提取的變化強度信息,進行多尺度變化信息模糊融合,得到最終的變化檢測結果。具體流程如圖1所示。

圖1 多尺度分析變化檢測流程
2.1 影像分割與子對象生成
利用ESP2工具[7]我們可以獲得目標地物提取的幾個最佳分割尺度。再借助eCognition軟件,按照最佳分割尺度,利用影像光譜特征,對前后兩時相影像分別進行預分割。在雙時相影像中同一未變化地物受到成像條件差異的影響,分割邊界通常并不一致。而雙時相影像中變化地物的邊界本身也不一致。這些不一致的分割邊界對后續的變化檢測工作帶來一定的困難。為此,本文將前后時相影像分割結果進行疊置進一步生成子對象,以此解決分割邊界不一致問題。后續的分析處理中以子對象作為基本分析單元。
2.2 變化強度圖構建
采用影像的光譜特征結構相似度來描述雙時相影像間的差異性。結構相似度(Structural Similarity,SSIM)由Wang Zhou等[8]首次提出,主要用于圖像質量評價。SSIM通過兩向量的均值、方差、協方差來評定向量間的相似性程度,是一種基于結構信息的相似度評價方法,其定義為:
Vk=SSIM(T1,T2)
=[l(T1,T2)]α·[c(T1,T2)]β·[s(T1,T2)]γ
(1)
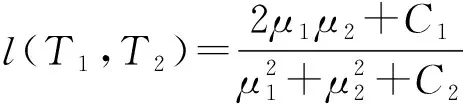

采用滑動窗口逐行計算雙時相影像間的光譜特征結構相似度,能充分利用像元的鄰域特征并減弱配準誤差帶來的影響。以子對象中所有像元的結構相似度均值作為該子對象的變化強度值構建變化強度圖。
2.3 多尺度變化強度模糊融合
本文引入模糊集理論以解決各尺度下同一空間位置像元變化情況判別結果沖突問題。采用常見的S型隸屬度函數[9]來計算隸屬度值,該函數為偏大型函數,在影像模糊分割處理時有較好的穩定性。假設在分割尺度為k時某像元的變化強度值為Vk(i,j),則該像元屬于未變化類別的隸屬度值為Mu(Vk(i,j)),同時屬于變化類別的隸屬度值為Mc(Vk(i,j))。隸屬度值間的關系為:Mu(Vk(i,j))=1-Mc(Vk(i,j)),且0≤Mc(Vk(i,j))≤1,0≤Mu(Vk(i,j))≤1。顯然,Mc(Vk(i,j))值越接近1,則變化強度值Vk(i,j)屬于變化類別的可能性就越大;反之,Vk(i,j)屬于未變化類別的可能性就越大[10]。公式(2)給出了變化強度值Vk(i,j)屬于變化類別的隸屬度值計算式。
(2)
上式中,將各分析尺度下的變化強度圖通過Otsu法獲得的分割閾值作為ck的取值,因大多數情況下影像中變化地物占比較小,因而令ak=0.8ck,bk=(ak+ck)/2且Mc(bk)=0.5。取3個分析尺度時,多尺度下的模糊隸屬度關系矩陣為:
(3)
采用文獻[11]的自適應融合策略,對3個尺度下的變化強度圖進行融合。利用各尺度下變化強度圖的灰度信息熵來計算某一尺度下的變化強度權值。基本原理為各灰度級的概率值p(j)相等時,灰度圖像的熵值最大。而變化強度圖上僅有變化和未變化兩種類別,因此,在變化強度圖上熵值越小越容易區分是否發生變化,因而熵值越小變化強度的權值越大。若3個尺度下對應的變化強度圖的熵值分別為H1、H2、H3。則每個尺度變化強度圖的自適應權值Wi可按下式計算:
(4)
式中Hi為各尺度下變化強度圖的熵。設某一影像有N個灰度級,且灰度級n(0≤n≤N)出現的概率為p(n),則該圖像的信息熵Hi可按下式計算:
(5)
則多尺度變化檢測模糊加權融合結果為:
M(i,j)=(Mc(i,j),Mu(i,j))=WiR(i,j)
(6)
其中Mc(i,j)和Mu(i,j)為多尺度變化信息融合后,像元(i,j)屬于變化像元和未變化像元的加權隸屬度值。像元(i,j)是否為變化的多尺度融合結果,按如下規則判定:Mc(i,j)>Mu(i,j),則像元(i,j)為變化像元,反之為未變化像元。
3 實驗
3.1 數據預處理
選取了西安市城區某地的谷歌地圖影像和天地圖影像進行實驗(如圖2所示)。所選的影像數據為利用LSV(Loca Space Viewer)軟件下載獲得。兩期影像分別拍攝于2016年和2017年,其中時相1為天地圖影像,時相2為谷歌影像。前后兩期影像均為RGB三波段彩色影像,拍攝季節都是夏季,無云覆蓋且成像清晰,亮度基本一致,空間分辨率均為 0.6 m,可滿足城市變化檢測實驗的要求。

圖2 預處理后影像
3.2 最佳分割尺度分析
利用易康軟件的多尺度分割工具對兩時相影像進行分割,并結合ESP2插件對影像中主要變化地物植被的最佳分割尺度進行分析,獲得各影像的最佳分割尺度。城市地物復雜多樣,并不存在適合所有地物的最佳分割尺度。即使是單一類別地物也不存在唯一的最佳分割尺度(例如本文實驗中的主要變化地物植被),因此需要采用一系列最佳分割尺度組合,才能夠達到對某類地物合理刻畫。為了便于分析,本文將一系列最佳分割尺度進行簡化,保留大、中、小3種尺度。
基于本文實驗影像進行多次分割實驗,結果顯示最小分割尺度選擇60,形狀因子0.1,緊致度0.5時分割結果的形狀與實際地物輪廓較為吻合,即最佳分割尺度。以此為基礎進一步分析得到一系列的最佳分割尺度。
3.3 參數設置
雙時相影像的結構相似度計算中相關參數設置如下:α=β=γ=1,C1=C2=C3=0.001。各時相的多尺度分割采用易康軟件的分割結果,子對象生成及后續實驗均采用Matlab2017進行仿真實驗。
4 結果與討論
4.1 多尺度分割與子對象生成結果
利用ESP2工具進行最佳分割尺度估算,獲得各影像的一系列最佳分割尺度。對每一幅影像在多個最佳分割尺度中,保留大、中、小3個尺度進行進一步分析。保留的最佳分割尺度如表1所示。

各影像植被的最優分割尺度 表1
利用表1中所列最佳分割尺度,分別對兩時相影像進行多尺度分割,各尺度分割結果及子對象生成結果如圖3所示。
從分割結果來看,大、中、小3種尺度下,綠地與非綠地圖斑邊界都分割得較好,混合圖斑情況較少。不同尺度下,僅在綠地內部出現亞類區分邊界,比如將草地和林地劃分為同一圖斑或分為不同圖斑。將時相1與時相2的分割結果進行疊加,生成子對象并以RGB彩圖形式顯示如圖3(c)、(f)、(i)所示。圖中藍色圖斑即為有明顯變化的新生成子對象。

圖3 多尺度分割及子對象生成結果
4.2 多尺度變化信息融合
在3個尺度下分別計算雙時相影像的結構相似度,得到不同尺度下的變化強度圖,再將變化強度進行模糊化處理,最后進行多尺度變化信息加權融合,得到最終結果。各尺度下經模糊化處理后的變化強度圖如圖4(a)~(c)所示。圖4(d)為多尺度變化信息模糊加權融合結果。
從多尺度變化信息圖(圖4)及多尺度變化信息融合檢測精度(表2)可以看到,分割尺度越小檢測到的細碎圖斑就越多,誤檢率也越高。隨著尺度的增大噪點進一步減少,誤檢率也逐步降低。融合圖像在權值的影響下向著檢測目標的方向調整,總體精度、Kappa系數、虛警率等指標與未進行多尺度信息融合前相比都得到了一定程度的提高。

圖4 多尺度變化信息融合

多尺度變化信息融合檢測精度 表2
5 結 論
本文針對面向對象的變化檢測中最優分割尺度難以確定問題,提出了多尺度分析的變化檢測方法。該方法是對常規面向對象變化檢測方法的一種改進,它在一定程度上彌補了單一分割尺度變化檢測的不足,對面向對象的變化檢測具有一定的普適性。
在西安市2016年天地圖影像和2017年谷歌地圖影像組成的影像對上進行變化檢測實驗。分別采用大、中、小3種分割尺度進行變化檢測,并進行多尺度融合變化檢測,對檢測結果進行比較,實驗結果表明多尺度融合變化檢測比單一尺度變化檢測精度有明顯的提升。

