基于ADAMS與MATLAB的6R機器人運動學分析與軌跡規劃聯合仿真

顧海華 ，胡興柳 ，毛軍輝

1.鹽城工學院 電氣工程學院，江蘇 鹽城 224002；2.金陵科技學院 智能科學與控制工程學院，江蘇 南京 211169；3.南京郵電大學 自動化學院、人工智能學院，江蘇 南京 210003

隨著社會與科學技術的不斷發展，工業機器人已經成為生產制造和科學研究領域的熱點。研究機器人首先要對機器人進行運動學分析，而運動學分析通常分為正運動學分析與逆運動學分析。機器人的正運動學分析是已知關節驅動力或者力矩，求解機器人末端執行器的位姿，如標準D-H參數法與改進的D-H參數法等；逆運動學分析為已知末端執行器位姿，求解對應關節產生的位移，如Newton-Euler 法、Lagrange 法、Kane法等。這些方法被廣泛運用到眾多場景中，目前，在MATLAB 與ADAMS 中進行聯合仿真是有效分析機器人運動特性的一種方式［1］，其不但可以保證軌跡規劃的精確性，也可測試系統的各項特性［2］。

1 6R機器人改進D-H參數法建模

一般工業機器人均由轉動副和移動副組成，6R 機器人作為目前最為廣泛使用的工業機器人，其6 個關節均是由旋轉副組成。圖1 為6 自由度機器人的KUKA KR16 操作臂，可實現3 個空間位置和3個控件姿態的任意運動。

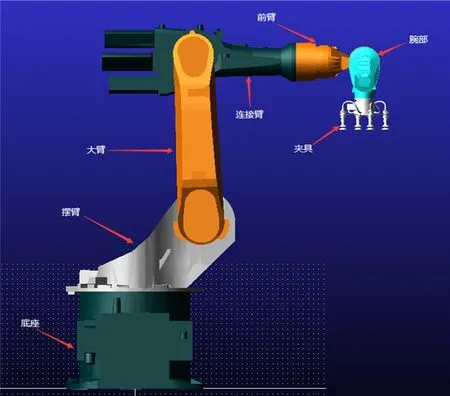
圖1 KUKA KR16操作臂Fig. 1 KUKA KR16 manipulator

在針對KUKA KR16 進行運動學分析前，需要建立其數學模型。為便于分析，建立機器人的連桿坐標系，如圖2 所示，即以機器人的第i- 1個關節的軸線Zi-1為Z軸，以Zi-1和Zi的公垂線Xi-1為X軸建立坐標系，其中X軸的方向為關節i- 1 指向關節i，而Y軸的Yi-1則按右手法則確定，即Yi-1=Zi-1?Xi-1。因此，坐標系中的每個連桿均可通過ai-1、αi-1、di和θi這4個參數進行描述，其中ai-1表示連桿長度，為Zi-1和Zi兩關節軸線之間的公垂線長度，αi-1表示連桿扭角，為Zi-1和Zi兩關節軸線之間的夾角，di表示相鄰兩關節之間的線位移，為Xi-1和Xi之間在Zi方向上的長度，θi表示相鄰兩關節之間的角位移，為Xi-1到Xi繞Zi轉過的角度。

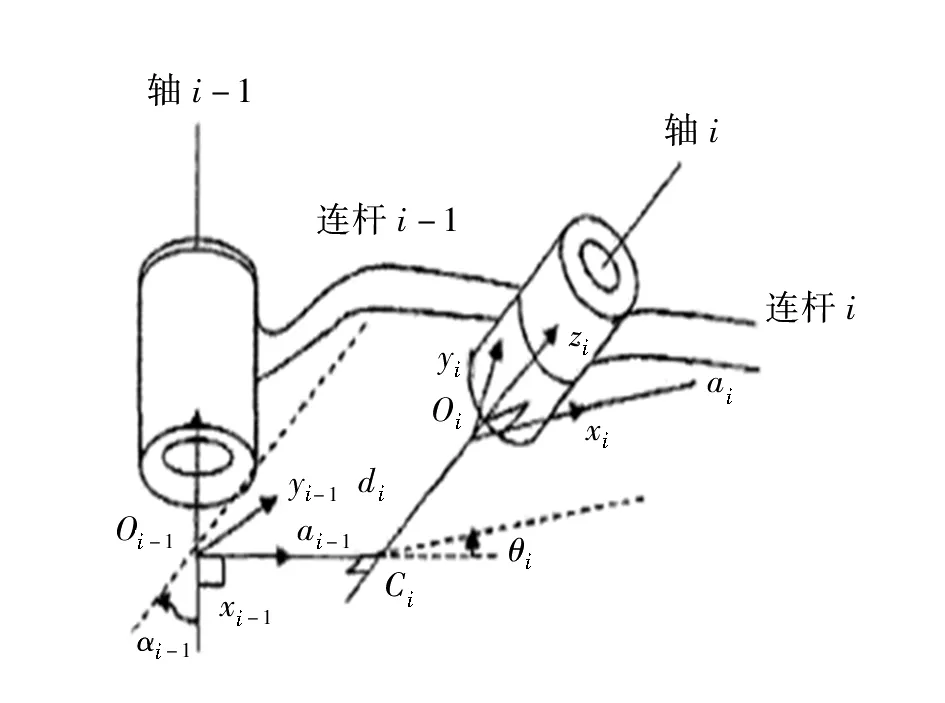
圖2 連桿坐標系Fig. 2 l ink-pole coordinate system

根據機器人的各項機械特性參數，采用目前使用最為廣泛的改進D-H 參數法，建立改進的D-H參數表［3］，如表1所示。

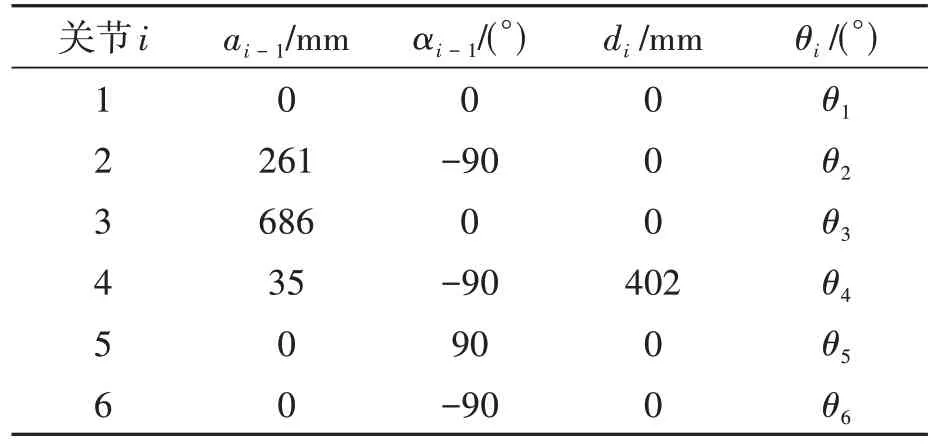
表1 改進的D-H參數表Table 1 Improved D-H parameters table

通過MATLAB中的Link和SerialLink函數建立KUKA KR16機械臂模型［4］。由于采用改進的D-H參數表，MATLAB中Link函數的一般表達式為L= Link([θi,d i,ai-1,αi-1,offset],′modified′)。

根據表1，可以得到Link 函數建立機械臂的命令為：

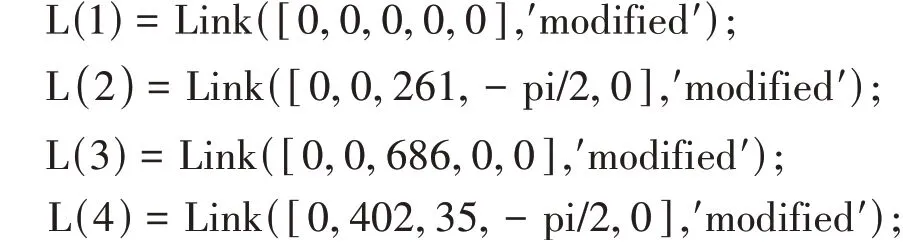
在MATLAB 中運行以上程序后，即可得到圖3所示的機器人模型。

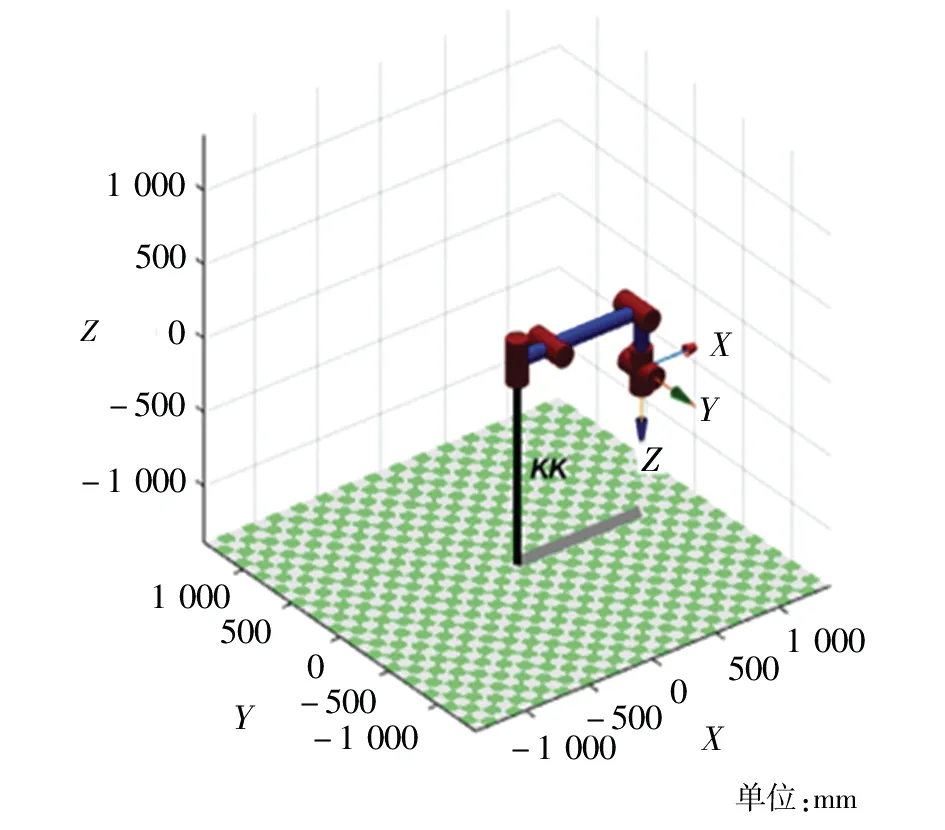
圖3 機器人MATLAB模型Fig. 3 Robot MATLAB model

2 6R機器人正、逆運動學分析

根據表1 和圖2、圖3 機器人各參數之間的關系［5］，可推導出兩個連桿坐標系之間的齊次變換矩陣，如式（1）所示。

將表1 數據帶入式（1），可以得出各個關節的變換矩陣，分別為：

根據機器人正運動學原理，機器人的關節變換矩陣可寫為：

式中：

根據機器人逆運動學中的反代數法，將機器人各關節變量分離出來，再逐次、逐個地求解出各個關節的關節變量(θ1，θ2，θ3，θ4，θ5，θ6)。具體求解方式如下：

設機器人初始位姿（機器人第1～6 個關節的角度）為θstart=[0，- pi/2， 0， pi， pi， 0]，通過正運動學方程求解，結果如式（10）所示；通過MATLAB/Robotics Toolbox 工具箱求解，結果如式（11）所示。

比較式（10）、式（11）可以看出，式（10）的二行二列為-1，式（11）的二行二列為1，其余各行各列的數值都相同。二行二列兩個數值的不同是因為機器人關節正反轉的不同，不影響最終位姿呈現的結果。故正運動學方程推導出的結果和MATLAB 工具箱求解的結果是一致的，證明了DH參數選取和齊次變換矩陣的正確性。

采用MATLAB/Robotics Toolbox 工具箱中的ikine 函數對機器人進行逆運動學計算，得到各關節的初始角度，如式（12）所示。由于運動學逆解存在不唯一解，在比較式（12）與初始位姿θstart=[0，- pi/2， 0， pi， pi， 0]時，可以發現式（12）與初始位姿θstart設定的結果基本一致。

3 6R機器人軌跡規劃

機器人軌跡規劃分為關節空間軌跡規劃與笛卡爾空間軌跡規劃。機器人運動軌跡確定方法很多，為獲得更高的平滑性，采用關節空間軌跡規劃中的五次多項式插值的方法進行軌跡規劃［6］。

設機器人各關節角位移函數為：

式中：s0、s1、s2、s3、s4、s5分別為五次多項式的系數。

對式（13）位移函數求一階導數，即可得到機器人各關節運動角的速度函數：對位移函數求二階導數即可得到機器人各關節運動角加速度函數：

為得到唯一的關節運動軌跡曲線，必須對其起始時刻的關節角度、關節角速度、角加速度共計6參數進行約束。

式中：θ0i為第i個關節的初始角度，（°）；為第i個關節的初始角速度，（°）/s；為第i個關節的初始角加速度，(°)/s2；θfi為第i個關節的終止角度，（°）為第i個關節的終止角速度，（°)/s為第i個關節的終止角加速度，（°)/s2；t0i為第i個關節運動的起始時刻，s；tfi為第i個關節從初始角度運動至終止角度的時間，s。

將式（16）帶入式（13）～式（15），得：

為得到機器人運動軌跡，在MATLAB 仿真前需先確定機器人各關節的初始角度θintial= [0，0，0，0，0，0]、終 止 角 度θtarget= [pi/2，pi/4，-pi/4，pi/3， pi/6，pi]、仿真時間10 s、采樣50 次，再根據式（17）及式（13）～式（15），在MATLAB 中仿真即可得出各關節對應的角度、角速度、角加速度的變化曲線，如圖4～圖6所示。

由圖4 可知，圖形準確地顯示了各關節的起始角度和終止角度；由圖5 可知，圖中曲線平滑，無突兀的激增和陡降，說明各關節角速度合適；由圖6可知，圖中曲線平穩變化。顯然，采用五次多項式插值的方法進行軌跡規劃是比較成功的［7］。

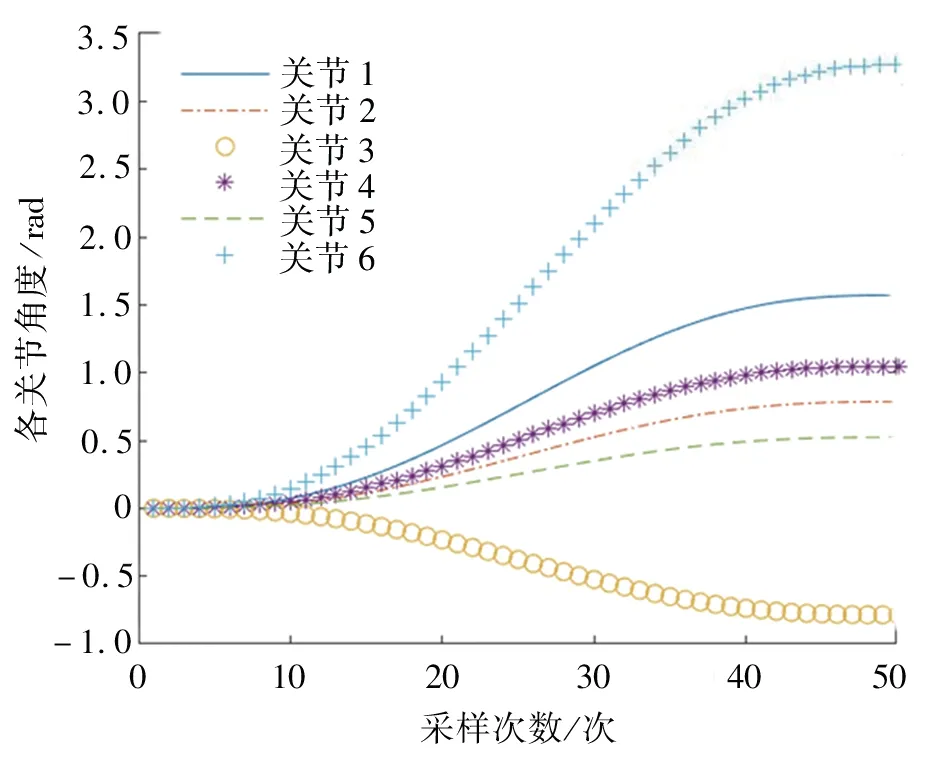
圖4 各關節角度軌跡規劃Fig. 4 Angle trajectory planning of each joint

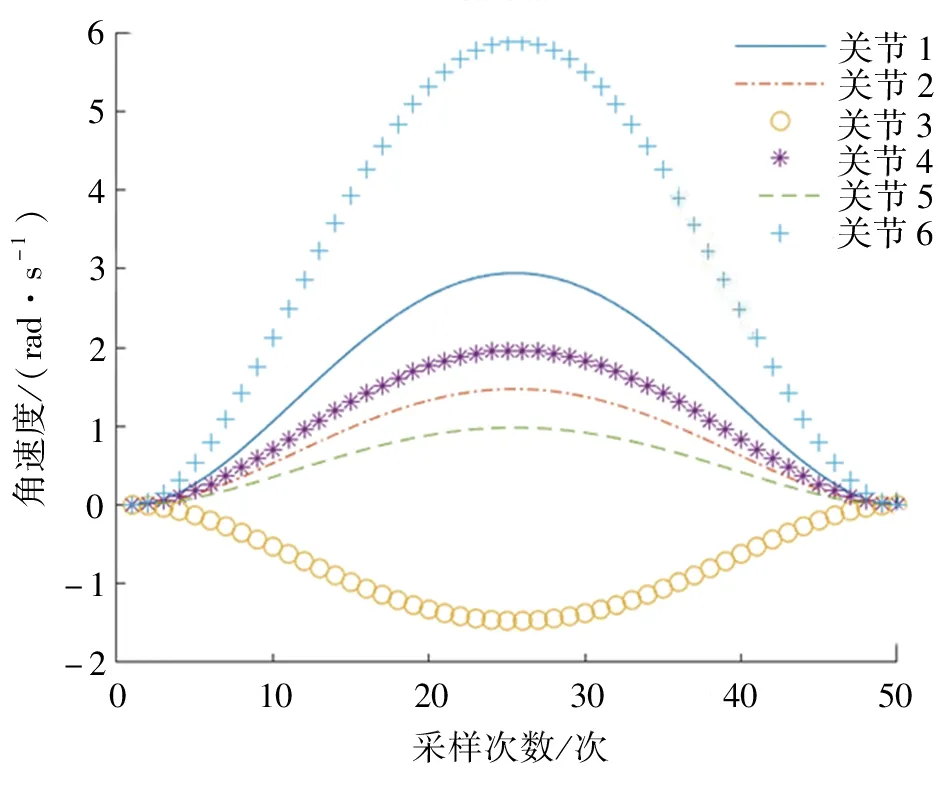
圖5 各關節角速度軌跡規劃Fig. 5 Angular velocity trajectory planning of each joint

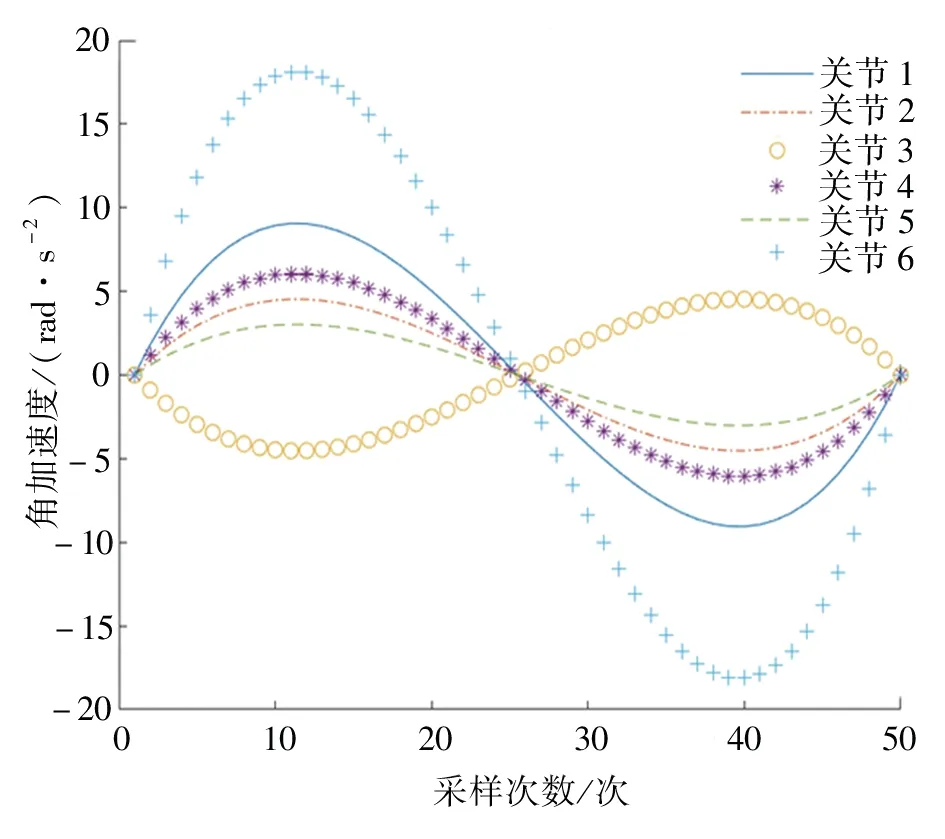
圖6 各關節角加速度軌跡規劃Fig. 6 Angular acceleration trajectory planning of each joint

4 ADAMS與MATLAB聯合仿真

ADAMS 是一款集建模、求解、可視化等技術于一體，在虛擬樣機領域被廣泛使用的軟件。利用ADAMS 軟件，用戶可以直接建立機械系統的幾何模型，或者從其他三維軟件（SolidWorks、Pro/E 等）中導入更為精細的模型［8］。本文利用Solid?Works 軟件建立模型并保存為Parasolid 格式，然后將其導入至ADAMS。需要注意的是，為使得仿真結果更貼近實際，同時還能減小計算量，通常在仿真之前先將細小的、零碎的、不影響仿真結果的部件刪除，然后將相關零件通過布爾和合為一體。另外，在模型導入至ADAMS 后，各零部件的材質、屬性、質量等參數都會丟失。因此，在模型導入至ADAMS 后，需要為每個零部件重新定義材質，并添加合適的約束。本文將所有材料屬性定義為steel，各關節之間均取旋轉約束（本文為6R機器人）。

利用MATLAB 軟件將五次多項式插值法軌跡規劃的數值計算出來，并將其保存為txt 格式，再導入至ADAMS 中；在ADAMS 中為各約束添加合適的驅動力后，利用ADAMS 中的spline 函數將各關節角度作用至對應的關節即可完成驅動，再利用軌跡工具畫出機器人運動軌跡線，如圖7～圖9 所示。機器人各關節之間的約束關系及驅動關系分別如表2～表3所示。

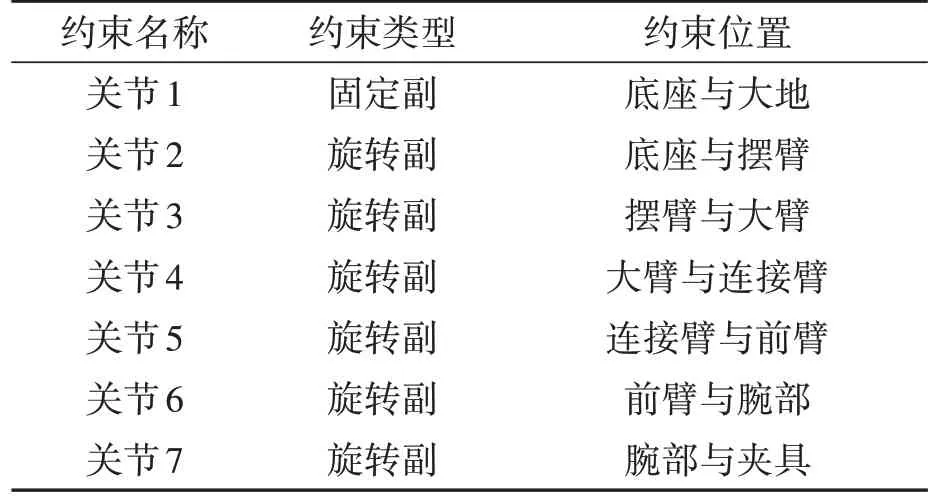
表2 機器人各關節約束關系Table 2 Constraint relation of each joint of robot

表3 機器人各關節驅動關系Table 3 Driving relationship of each joint of robot

對比圖7～圖9，可知各曲線的數值大小、弧度等都近似，說明聯合仿真比較成功。

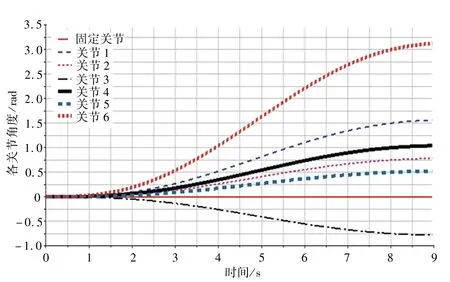
圖8 機器人各個關節在ADAMS中的角度曲線Fig. 8 Angles of each joint in ADAMS

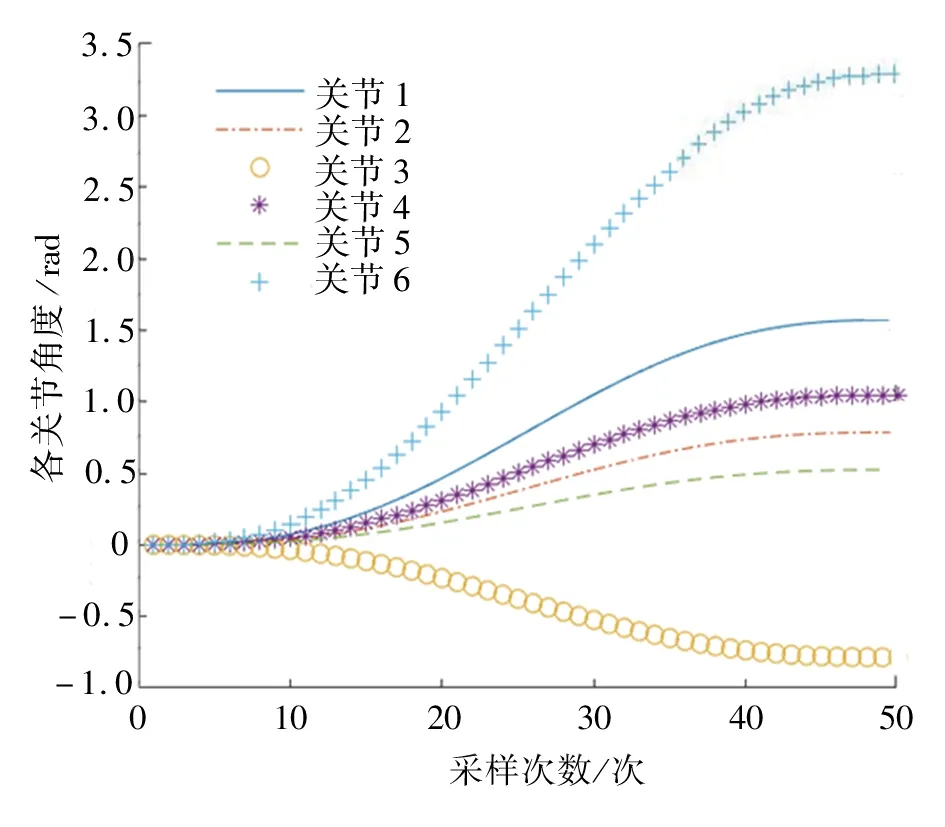
圖9 機器人各關節在MATLAB中的角度曲線Fig. 9 Angles of robot joints in MATLAB

在ADAMS 軌跡規劃中，也可使用“一般點驅動”功能對機器人進行軌跡規劃［9-10］，操作步驟為：在模型的末端執行器上設置一個標記點，在該標記點上添加“一般點驅動”，在驅動編輯里設置相應的驅動方程。

利用“一般點驅動”功能對常見且較為復雜的圓錐螺旋曲線進行仿真，步驟如下：

（1）確定圓錐螺旋曲線的數學表達式

式中：S為螺旋線導程，mm；T為運動周期，s；a為螺旋曲線的螺距，mm；t為仿真時間，s。

（2）設置相關參數：螺旋線導程S= 30 mm，運動周期T= 2s，螺旋曲線的螺距a= 15 mm，仿真時間t=6 s，步數300步。

（3）選擇交互仿真。

仿真結束后在末端執行器上通過軌跡工具即可得到末端執行器的運動軌跡曲線，如圖10所示。

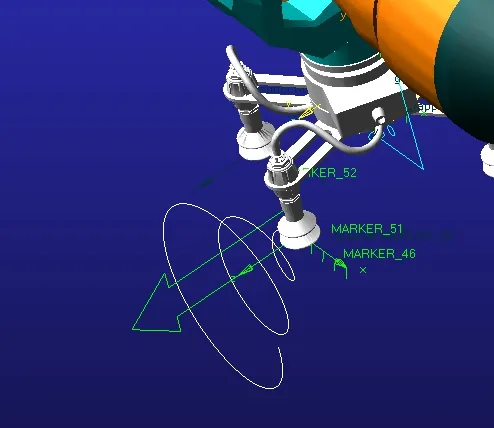
圖10 機器人末端執行器軌跡Fig. 10 Trajectory diagram of robot end-effector

在ADAMS 中，也可以使用spline 函數進行仿真，方法如下：清除之前設置的點驅動，導入6 個關節的角度spline 函數，給每個關節添加相對應的驅動（驅動函數由spline 函數完成），并設置仿真時間6 s，步數300 步［11］。通過DX、DY、DZ 函數得到末端執行器在X、Y、Z軸方向上的運動曲線，如圖11 所示；通過Ax/Ay/Az Projected Rotation 得到機器人各關節角度變化曲線，如圖12 所示；通過Relative Angular Velocity 得到機器人各關節角加速度變化曲線，如圖13所示。

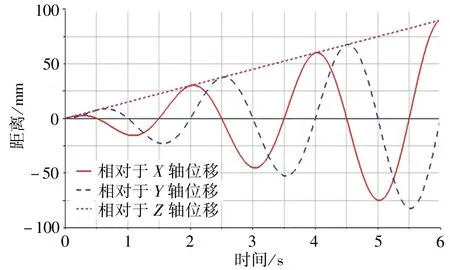
圖11 機器人末端執行器運行曲線Fig. 11 Running curve of robot end-effector

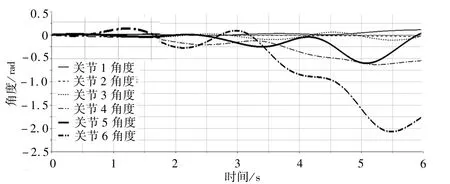
圖12 機器人各關節角度變化曲線Fig. 12 Angle variation curve of each joint of robot

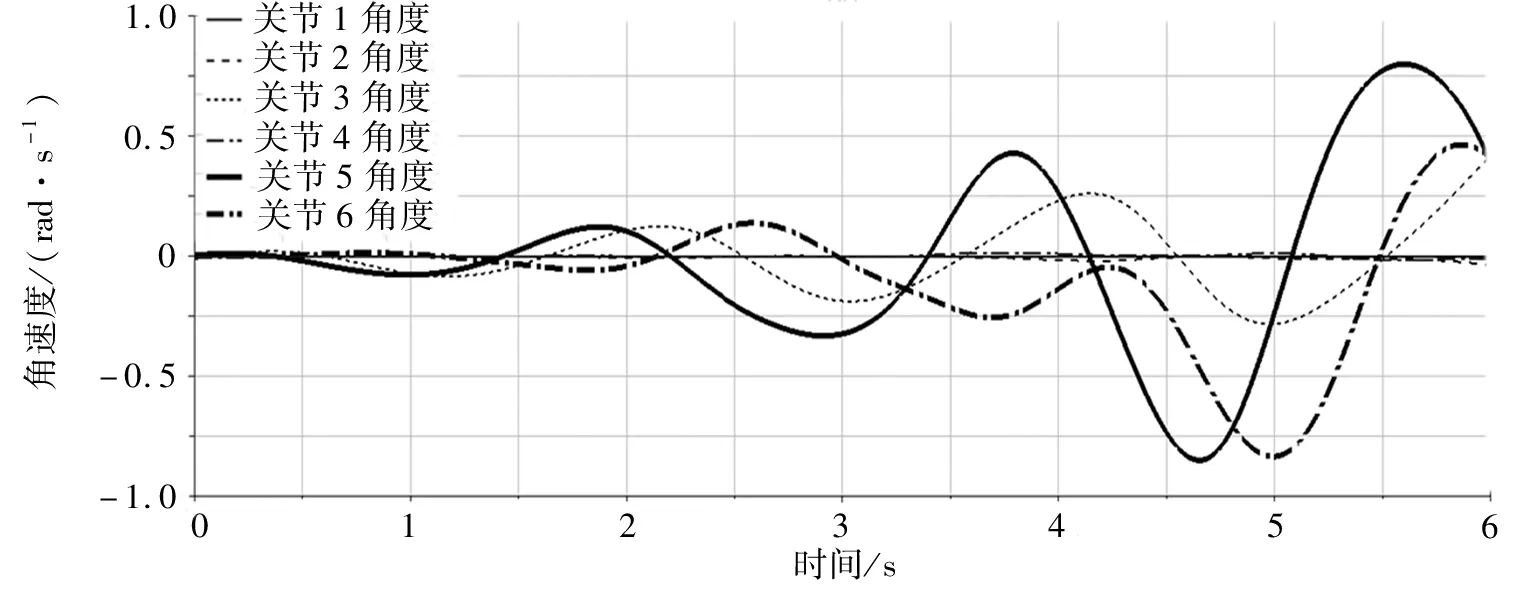
圖13 機器人各關節角速度變化曲線Fig. 13 Angular velocity curve of each joint of robot

將圖11～圖13 與圖10 進行對比，可知仿真結果正確。

在ADAMS 中，通過“一般點驅動”與spline 函數的2次仿真，可以發現仿真目標均為空間形狀，仿真后最終所呈現的末端執行器的運行軌跡與機器人運動學分析相符，說明ADAMS 下運動學仿真分析是正確的，驗證了從SW 導入至ADAMS的KUKA KR16機器人模型的可靠性。

5 結論

針對6 自由度工業機器人的運動學與軌跡規劃問題，在改進的D-H 參數法基礎上，通過矩陣的齊次變換推導出機器人的運動學方程，再通過正逆運動學進行求解；采用MATLAB/Robotics Toolbox 工具箱對機器人進行正逆運動學求解，驗證了運動學方程的正確性，再通過五次多項式插值法進行軌跡規劃；最后在ADAMS 中導入KUKA KR16 機器人的3D 模型，利用ADAMS 與MATLAB 聯合仿真技術驗證了運動學模型的正確性。