醫療應急物資車輛配送優化調度時間窗模型研究*

吳 坷，宋英華，呂 偉

(1.武漢理工大學 中國應急管理研究中心，湖北 武漢 430070；2.武漢理工大學 安全科學與應急管理學院，湖北 武漢 430070)

0 引言

突發事件的發生不僅會對人類的正常生活造成巨大的影響，并且嚴重情況下還會造成社會的重大人員傷亡以及經濟損失。如2020年發生的新冠肺炎疫情，截至2020年3月份，疫情僅發生2個月，武漢的新冠肺炎確診人數就已高達48 137人，死亡2 132人，GDP增速相比2019年同期下降超過2%[1]。應急物資配送是突發事件應急過程中1項很重要的因素，其影響著整個應急環節的效率，同時，保證應急配送效率是面對突發事件采取行動成效的關鍵一環。

在滿足時間窗約束的應急物資車輛配送研究方面，國內外學者目前已做了大量研究，對于時間窗下的應急物資配送路徑問題的研究，主要包括受災點需求時間窗約束問題[2-6]和配送成本及距離最小等問題[7-9]。在考慮時間窗的車輛配送路徑研究中，Maxmilian Marius等[10]在研究考慮車輛路徑問題時，最先提出了時間窗的想法，并運用啟發式算法進行求解；李善俊等[11]求解多目標車輛路徑優化模型時，考慮了車輛載重、時間窗、生鮮品保質期等多約束條件，并運用改進的非支配排序遺傳算法進行求解；蔣祿歡[12]提出需求拆分、多時間窗和集送貨同時約束的車輛配送模型，解決了考慮時間或距離的單一約束條件不足的情況；鮑偉等[13]以車輛和車輛運輸及等待時間懲罰3者成本最小為目標，建立軟時間窗約束下的多車型車輛配送模型；Yannis等[14]研究帶時間窗的配送路徑時提出了1種多自適應粒子群優化算法，該算法采用了3種不同的自適應策略；曹慶奎等[15]考慮實際交通中交通流和客戶時刻發生改變的情況，對交通流的多模糊時間窗車輛路徑問題展開研究；呂偉等[16]考慮不同需求點的不同時間窗，以最大化時間和需求的滿意度為目標，兼顧救援的公平性原則，運用亞當斯的公平分配理論進行計算；王濤等[17]考慮車輛配送問題時，以配送費用和配送車輛數最少為條件，提出改進的智能水滴遺傳混合算法；龐燕等[18]構建雙目標數學模型，考慮行駛距離和車輛數最少，提出改進的2階段禁忌搜索算法進行求解；戴意愿等[19]考慮乘客運輸車輛路徑規劃問題時，對乘客運輸需求不定以及出發站點和目標站點的隨機性，提出基于粒子群算法的車輛路徑規劃策略。

在整個應急物資配送系統中，配送過程往往不是獨立存在的，而是會受到很多因素的影響，其中考慮時間窗約束與配送車輛的數目結合，得到整體優化調度協同方案較少。在突發事件發生后，需同時考慮不同時間窗約束和最少配送車輛數即最少數目的配送通路，才能更全面地、更合理且高效地完成整體路網的應急物資配送。

本文提出的考慮時間窗影響的應急物資車輛優化調度方案，所快速得到完整的應急物資車輛優化調度模型，使得所需的應急物資能在要求的時間窗內抵達目的地，同時保證因為車輛數目及配送路徑造成的成本最低。

1 問題描述

1.1 本質問題

突發事件發生后，在任一路網中，存在多個應急物資配送中心和應急物資需求點，現將儲備在各個應急物資配送中心的應急物資按照時間窗的要求，由車輛配送至各個物資需求點，在多個單循環配送路徑中，找到最少數目的配送車輛即配送通路(將可有1輛車完成的多個單循環配送連接起來，成為1個配送通路)。

1.2 多配送中心車輛配送問題

考慮更加符合實際城市交通路網情況的應急物資車輛配送問題，即存在多個應急物資配送中心的供給時間窗應急物資車輛配送問題。

配送示意圖如圖1所示。

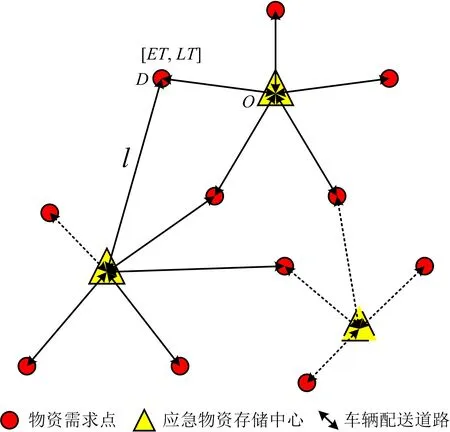
圖1 配送示意Fig.1 Schematic diagram of distribution

如圖1所示，在1個路網中，有多個配送中心和物資需求點。從某1配送中心出發的車輛需在時間窗[ET，LT]抵達相對應的物資需求點后，返回該配送中心方可對下一物資需求點進行配送，同時到達各物資需求點的時間均滿足該點時間窗要求。存在車輛在配送中心的等待時間，在此情況下得到多種配送方案，最終找出最少配送車輛，即最少配送通路。

圖1中，O為配送中心；D為需求點；[ET，LT]為物資需求點的約束時間窗，其中ET為要求的物資最早到達時間(ET可以為0)，min；LT為要求的物資最晚到達時間，min；l為配送道路，km；虛線為省略的配送中心和配送需求點及配送路線。

2 模型研究

2.1 模型假設

側重研究突發事件下，時間窗約束對應急物資配送路徑的綜合影響，考慮配送車輛數最少即通路數最少的情況，并作如下假設:

1)配送中心儲備充足，對需求點的單獨配送可滿足需求量。

2)從配送中心至物資需求點配送的車輛容量足夠大即單車運力可完成1次配送。

3)各物資需求點的需求物資種類不同，不存在沿路配送的可能，所有配送車輛均需完成對當前需求點的配送任務后返回配送中心，方可為新的需求點服務。

4)各物資需求點對物資的需求存在時間窗，物資必須在要求的時間窗內送達方為有效。

5)路網確定，不考慮道路損毀，交通狀態良好。

6)配送車輛的配送速度一定，且均速進行配送。

7)在配送過程中需滿足時間窗要求；因存在車輛從0時出發時到達需求點時不滿足時間窗要求，故存在車輛在配送中心的等待時間。

8)在車輛配送時，因為車輛有限，優先配送等待時間短的需求點，即滿足7)的所有需求點中，優先配送等待時間短的需求點。

2.2 模型構建

相關符號說明如下

1)集合

O={i|i=1,2,…,n}為配送中心集合；

D={j|j=1,2,…,n}為物資需求點集合；

R={m|m=1,2,…,n}為配送道路集合；

H={h|h=1,2,…,n}為物資配送車輛集合。

2)相關參數

lij表示從配送中心Oi到物資需求點Dj的距離最短路徑長度，km；

dRm表示路段Rm的長度，km；

vRm表示路段Rm的車輛實際行駛速度，km/h；

wh表示車輛h在配送中心等待的時間，min。

ETj表示Dj要求物資到達的最早時間，min；

ELj表示Dj要求物資到達的最晚時間，min；

TOiDj表示從起點Oi出發，到點Dj的所用的時間，min；

FOiDj表示從起點Oi出發，到點Dj然后返回Oi點的過程所用的時間，min；

FjOiDj表示需求點Dj被完成配送時，配送車輛返回起點Oi所需的時間，其中共經過j個需求點，min；

k表示完成配送點Dj時的上1個完成配送的需求點。

3)目標函數

目標函數如式(1)所示：

(1)

式(1)目標函數表示車輛優化調度方案所使用的車輛數最小。

式(2)～(6)為約束函數：

ETj≤Fj-1OiDk+TOiDj+wh≤ELj

(2)

(3)

(4)

(5)

(6)

式(2)表示完成物資需求點Dj配送所需滿足的時間窗約束，其中當j-1為0時，Fj-1ODk=0；式(3)表示對于任意車輛只能使用1次；式(4)表示對于任意1個需求點，只能被1輛車配送1次；式(5)表示對于任意1個需求點Dj只有1個配送中心點Oi為其提供物資;式(6)表示對于任意1個配送中心Oi至少對1個受災點Dj進行物資配送。

式(2)中參數如式(7)～(8)所示：

TOiDj=dRij/vRij

(7)

FOiDj=2TOiDj

(8)

在該模型中，dRm，vRm，ETj，ELi是已知量，lij，TOiDj是可觀測量。

2.3 問題求解

針對所構建的數學模型，設計如下求解方案：

1)計算路網中所有配送中心Oi到對應物資需求點Dj的所有最短路徑集合R；

2)根據R計算從配送中心Oi出發到相應物資需求點Dj的所有配送時間TOiDj(從物資需求點返回至配送中心的時間與配送中心出發至物資需求點的時間一致；

3)運用MATLAB編程滿足模型要求的代碼，將路網信息，如時間窗約束條件，道路信息集合R，配送時間TOiDj導入編號的程序模型中，可得到車輛優化調度方案；

4)得到的優化調度方案中包括最少配送車輛、車輛對應出發點及對應配送編號、需求點等待時間集合、車在配送中心的等待時間集合；

5)對比各個優化調度方案，通過對比成本可以得到各個方案的優劣排序，從而得到最優方案。

3 情景應對分析

3.1 情景構建

2020年1月23日上午10時，武漢市因新冠肺炎疫情影響，最先開始“封城”，截止1月26日，湖北城市地區都進入“封城”狀態。因疫情發生，湖北省各地出現防疫物資緊缺的情況，由于“封城”影響，交通不暢。假設防疫物資集中在應急物資儲備中心處，需由應急車輛統一進行防疫物資配送，湖北省疫情災害情景如表1所示。

表1 湖北省疫情災害情景簡介Table 1 Brief introduction of epidemic disaster scenario in Hubei province

選取湖北省13個地級行政區以及4個省直轄縣級行政單位作為研究對象，以湖北省經濟較發達的3個市作為應急資源配送中心，分別是武漢市、宜昌市、襄陽市，以這3個配送中心向其他地區進行應急物資配送，如圖2所示；然后根據實際路網信息建立拓撲圖，如圖3所示。

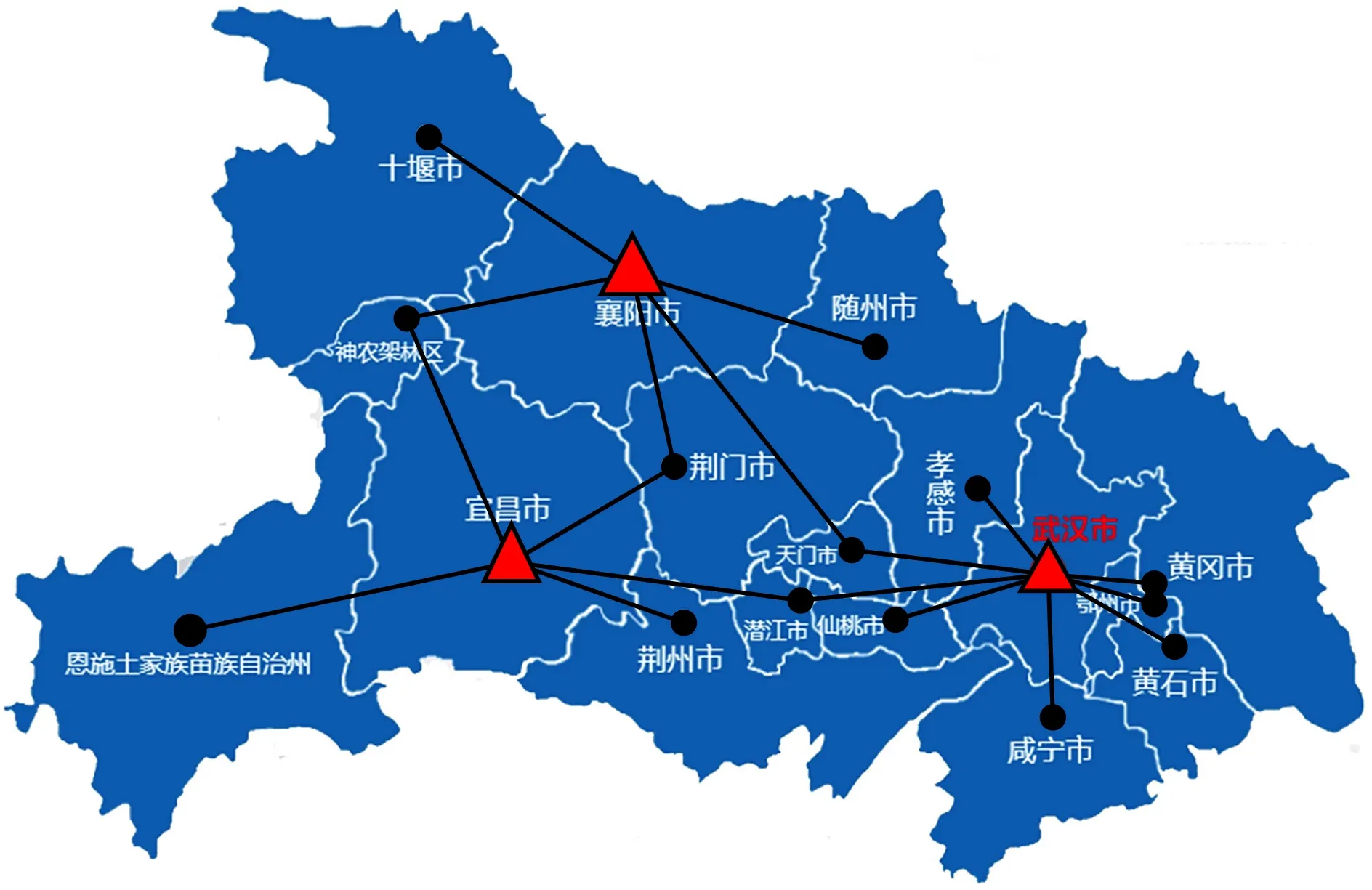
圖2 湖北省防疫物資配送網絡Fig.2 Distribution network of epidemic prevention materials in Hubei province

圖3 湖北省配送路網拓撲Fig.3 Topology diagram of distribution road network in Hubei province

3.2 應急物資車輛優化調度方案求解

該路網共3個應急物資儲備中心，14個應急物資需求點，18段路，由配送中心出發沿高速公路行駛至配送點的實際距離，可知每條配送道路的實際距離，車輛平均速度取100 km/h，根據每條道路的距離，則可得到車輛在該段道路所行駛的時間，結果取整數，路網及車輛行駛時間的具體信息如下表2所示。

表2 車輛行駛道路信息Table 2 Information of vehicle driving roads

為方便研究，隨機擬定每個應急物資需求點的時間窗要求區間，允許時間窗起始時間為0，具體信息如下表3所示。

表3 防疫物資需求點信息Table 3 Information of demand points for epidemic prevention materials

運用MATLAB R2016b編程進行方案求解步驟的處理，求解目標函數進行計算，經過多次運行后得到運行結果，運行結果顯示，最少配送車輛數為11輛，共有8種配送方案，車輛具體分配情況如表4所示：

表4 配送車輛分配情況Table 4 Assignation of distribution vehicles

湖北省防疫物資配送車輛優化調度方案如表5所示，括號內為車輛在配送中心等待的時間；“；”隔開的配送路徑指的是從該配送中心出發，不同車輛完成的1次配送通路。

從表5可得，方案1中，第1輛車從O1，0時出發開始配送D1；第2輛車從O1，0時出發開始配送D2；第3輛同理可得方案2～方案8的車輛優化調度方案。

表5 湖北省防疫物資配送車輛調度方案Table 5 Scheduling scheme for distribution vehicles of epidemic prevention materials in Hubei province

車從O2，0時出發開始配送D3；第4輛車從O2，等待1 min后出發依次配送D4，D7；第5輛車從O2，0時出發配送D6；第6輛車從O3，0時出發配送D5；第7輛車從O3，等待5 min后出發依次配送D8，D13；第8輛車從O3，等待12 min后出發配送D9；第9輛車從O3，0時出發配送D10；第10輛車從O3，0時出發配送D12；第11輛車從O3，0時出發依次配送D14，D11。

在得到該路網在時間窗約束條件下，最少可由11輛車完成所有需求點的配送以及8種不同的配送方案，現對比這8種方案的車輛行駛距離，計算配送成本，可得到最優方案及優劣排序。表6為這8個方案的總配送距離。

表6 配送距離對比Table 6 Comparison of distribution distance

由表6可知，因方案2的配送總成本最少，所以方案2為最優方案。方案2的配送示意如圖4所示，圖中直線雙箭頭為車輛單獨配送的路線，黑色曲線箭頭和黑色虛線箭頭為由1輛車完成的需求點配送，序號①～④表示車輛行走路線順序。

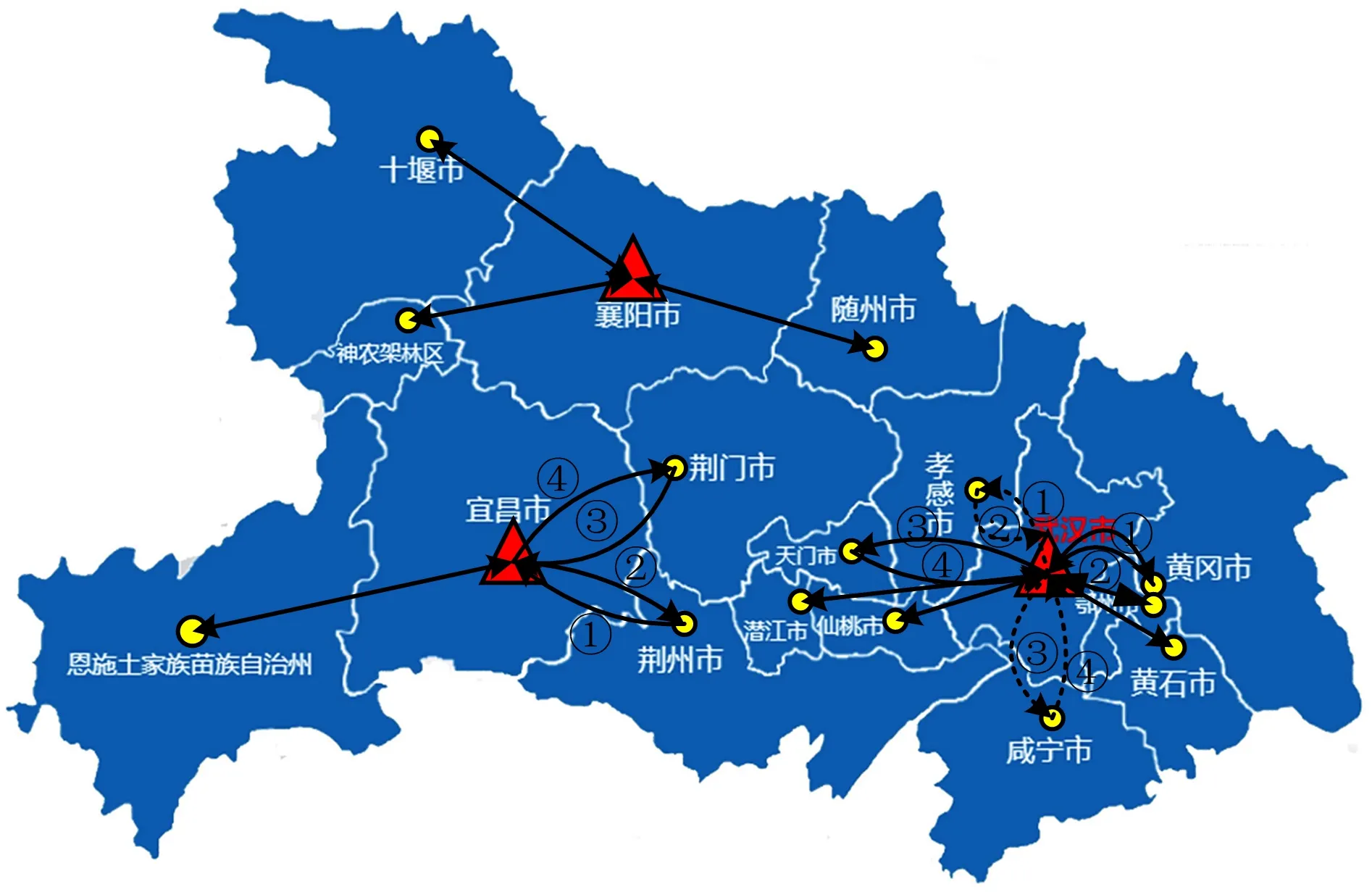
圖4 方案2配送示意Fig.4 Schematic diagram of distribution with scheme 2

4 結論

1)在原有時間窗要求的車輛路徑問題基礎之上突破傳統的單時間窗要求對尋求最短時間路徑的局限，通過考慮多時間窗的方式尋求滿足實際情景要求的交通管制方式和運輸路線，以尋找最優可行解。

2)將經典的LRP問題與實際道路交通配送時的車輛問題相結合，從新穎的優化車輛數的角度入手，擺脫傳統理論模型拘泥于路徑的重復選擇和不計運輸成本的假設，更加貼近于事實情景且具有現實意義。

3)在現有的基礎問題之上考慮供給時間窗問題，后續研究可以繼續考慮道路破損情況以及道路實時信息不斷發生變化的可能，使得到的結果更加普遍及精確。