不同圍壓條件下淤泥質(zhì)黏土蠕變力學特性試驗及模擬*

李 春，譚維佳

(1.重慶市建筑科學研究院有限公司，重慶400016；2.長安大學 地質(zhì)工程與測繪學院，陜西 西安 710054)

淤泥質(zhì)黏土是碼頭常見地基土，在應力作用下不僅會瞬間發(fā)生變形，還會隨著時間推移而累積蠕變變形，威脅碼頭工程的長期穩(wěn)定和安全[1-2]。研究淤泥質(zhì)黏土蠕變特性，對控制淤泥質(zhì)黏土地基沉降具有重要的工程意義[3]。

目前對于淤泥質(zhì)黏土蠕變特性研究已有一定成果，李軍世等[4]以上海淤泥質(zhì)黏土為研究對象，選取合理經(jīng)驗參數(shù)，建立具有適用性的Singh-Mitchell蠕變經(jīng)驗模型；朱登峰等[5]對淤泥質(zhì)黏土進行循環(huán)蠕變試驗，研究蠕變應變特征和孔壓變化規(guī)律；Wang等[6]開展天津濱海地區(qū)淤泥質(zhì)軟黏土蠕變試驗，基于元件模型建立了非線性蠕變本構(gòu)模型；賴華輝[7]研究不同干密度下的膨脹土蠕變特性，分析干密度對蠕變變形、蠕變速率、長期強度的影響；李碩等[8]研究上海淤泥質(zhì)黏土固結(jié)蠕變過程中水和微機構(gòu)變化規(guī)律，為淤泥質(zhì)黏土宏觀蠕變研究提供微觀參考依據(jù)。

本文以某遮簾式板樁碼頭工程淤泥質(zhì)黏土為研究對象，制備飽和重塑樣，開展固結(jié)排水三軸壓縮蠕變試驗，分析淤泥質(zhì)黏土應變特征、蠕變速率和等時軸壓-軸向應變關系，結(jié)合淤泥質(zhì)黏土的等時軸壓-軸向應變雙曲線形態(tài)特征，分別引入Mesri和Log-Modified模型辨識蠕變數(shù)據(jù)，給出兩者模型參數(shù)求解方法，分別得到適用于本文淤泥質(zhì)黏土的Mesri和Log-Modified蠕變經(jīng)驗模型，對比兩者蠕變經(jīng)驗模型辨識效果，給出本文碼頭工程淤泥質(zhì)黏土的推薦蠕變模型。研究成果可為淤泥質(zhì)黏土蠕變特性研究及碼頭地基設計、施工及后期運營提供一定參考。

1 淤泥質(zhì)黏土蠕變試驗

1.1 試驗材料及方案

本文淤泥質(zhì)黏土取自某遮簾式板樁碼頭工程，其基本物理力學參數(shù)見表1。蠕變試驗之前，根據(jù)取樣深度完成先期k0不等向固結(jié)條件(k0為土的靜止側(cè)壓系數(shù))，取k0=0.5。

表1 淤泥質(zhì)黏土基本物理力學參數(shù)

根據(jù)《土工試驗方法標準》[9]，制備直徑39.1 mm、高80 mm的飽和重塑樣，蠕變試驗采用SR-6型土體三軸流變試驗機，蠕變試驗方案見表2。

表2 蠕變試驗方案

由表2可看出，本文試驗分為兩步：1)固結(jié)。首先對重塑飽和土樣施加圍壓，完成等向固結(jié)后再依據(jù)先期k0固結(jié)條件，將軸向荷載緩慢加至目標值，完成k0不等向固結(jié)。2)蠕變。依據(jù)表2的試樣方案控制軸壓和圍壓的變化，蠕變穩(wěn)定后再施加下一級軸向荷載直至破壞，每一級加載均維持在90 h以上，本文淤泥質(zhì)黏土在第5級加載時破壞，3種圍壓下的破壞偏應力(σ1-σ3)f分別為300、400和500 kPa。為便于后文蠕變模型辨識及參數(shù)求取，再進行固結(jié)排水三軸壓縮試驗，確定3種圍壓條件下的剪切強度，分別為523、736和945 kPa。

1.2 試驗結(jié)果

蠕變試驗數(shù)據(jù)由三軸試驗機數(shù)據(jù)系統(tǒng)采集，得到分級加載全過程曲線，如圖1所示。

圖1 逐級軸向加載蠕變曲線

由圖1可看出，3種圍壓下的蠕變曲線軸向應變存在一個初始值，這是由于淤泥質(zhì)黏土蠕變試驗是完成先期不等向固結(jié)后進行的。蠕變試驗中，淤泥質(zhì)黏土在軸壓提升的短暫時間內(nèi)，軸向應變瞬間增大，這部分軸向應變?yōu)樗矔r應變。隨著加載時間的增長，土樣表現(xiàn)出衰減蠕變行為，應變率逐漸降低，應變率趨于穩(wěn)定后土樣便進入了穩(wěn)定蠕變階段，土樣在衰減和穩(wěn)定蠕變階段的軸向應變?yōu)槿渥儜儭?/p>

2 試驗結(jié)果分析

2.1 分別加載蠕變曲線

通過Boltzmann線性疊加原理[10]處理后的分級加載蠕變曲線如圖2所示。

圖2 分級加載蠕變曲線

由圖2可看出，淤泥質(zhì)黏土不同圍壓不同加載等級下的蠕變曲線形態(tài)較相似。同一圍壓下，隨著軸壓的提升，軸向應變逐漸遞增。同一加載等級下，圍壓和軸壓的升高促進軸向應變的增長。

2.2 蠕變速率

蠕變速率求取引用文獻[11]中的計算方法：

(1)

式中：εn為蠕變應變；n為蠕變試驗應變數(shù)據(jù)個數(shù)；Δε為蠕變應變差值之和；Δti為蠕變時間；vi為蠕變速率。

利用式(1)在圖2的基礎上進行計算，繪制蠕變速率曲線，如圖3所示。

由圖3看出，蠕變速率曲線分為衰減和穩(wěn)定蠕變階段兩個部分，衰減蠕變階段存在一個較高的初始蠕變速率，在10 h內(nèi)逐漸衰減，接著進入穩(wěn)定蠕變階段，10～90 h蠕變速率基本保持恒定。在同一圍壓下，隨著加載等級的提升，衰減和穩(wěn)定蠕變階段的初始蠕變速率和穩(wěn)態(tài)蠕變速率均逐漸增大。

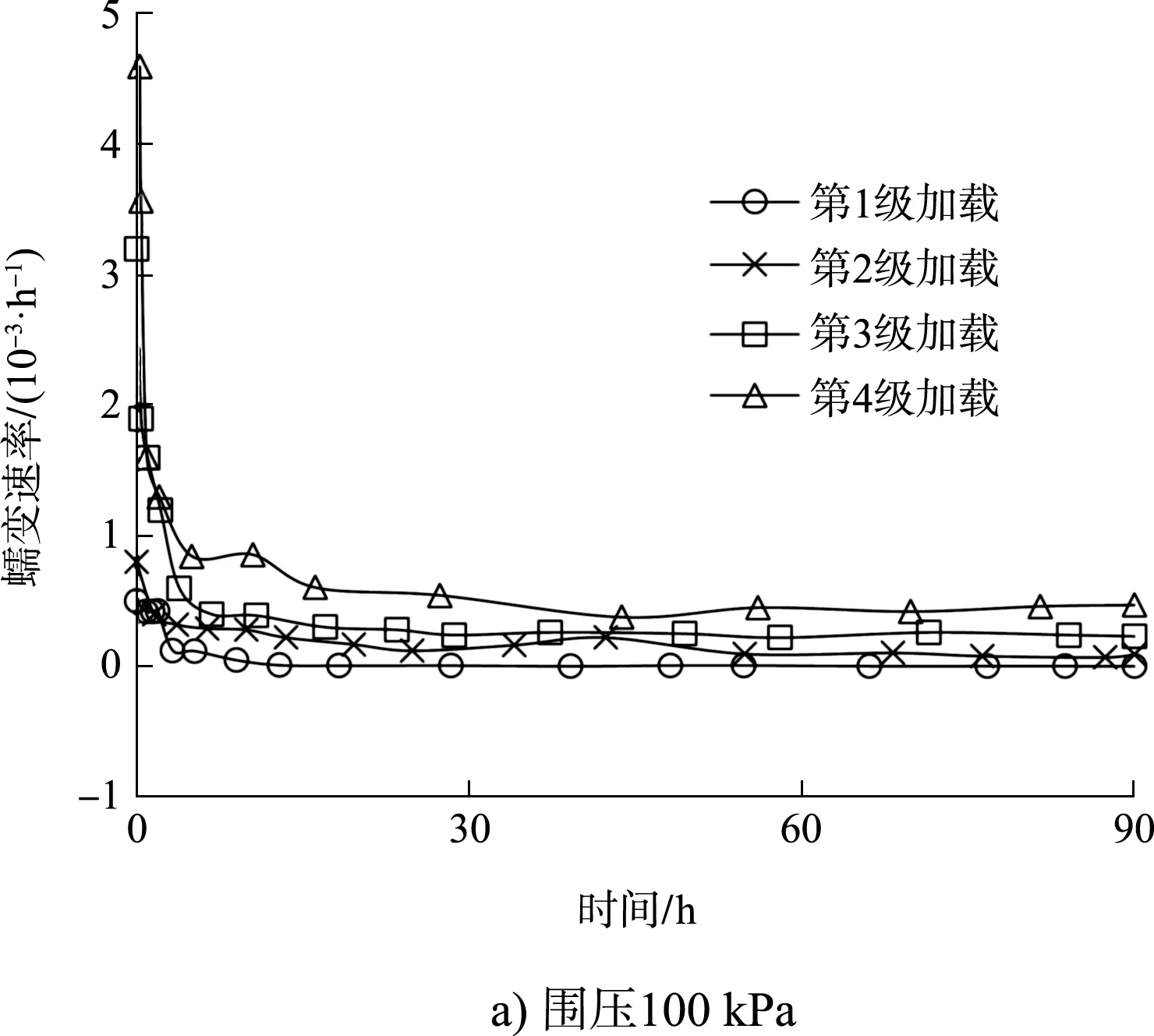
圖3 分別加載蠕變曲線

為研究初始蠕變速率、穩(wěn)態(tài)蠕變速率與圍壓、軸壓之間的關系，選取圖3中的穩(wěn)態(tài)蠕變速率平均值及初始蠕變速率，繪制相對應的曲線如圖4所示。

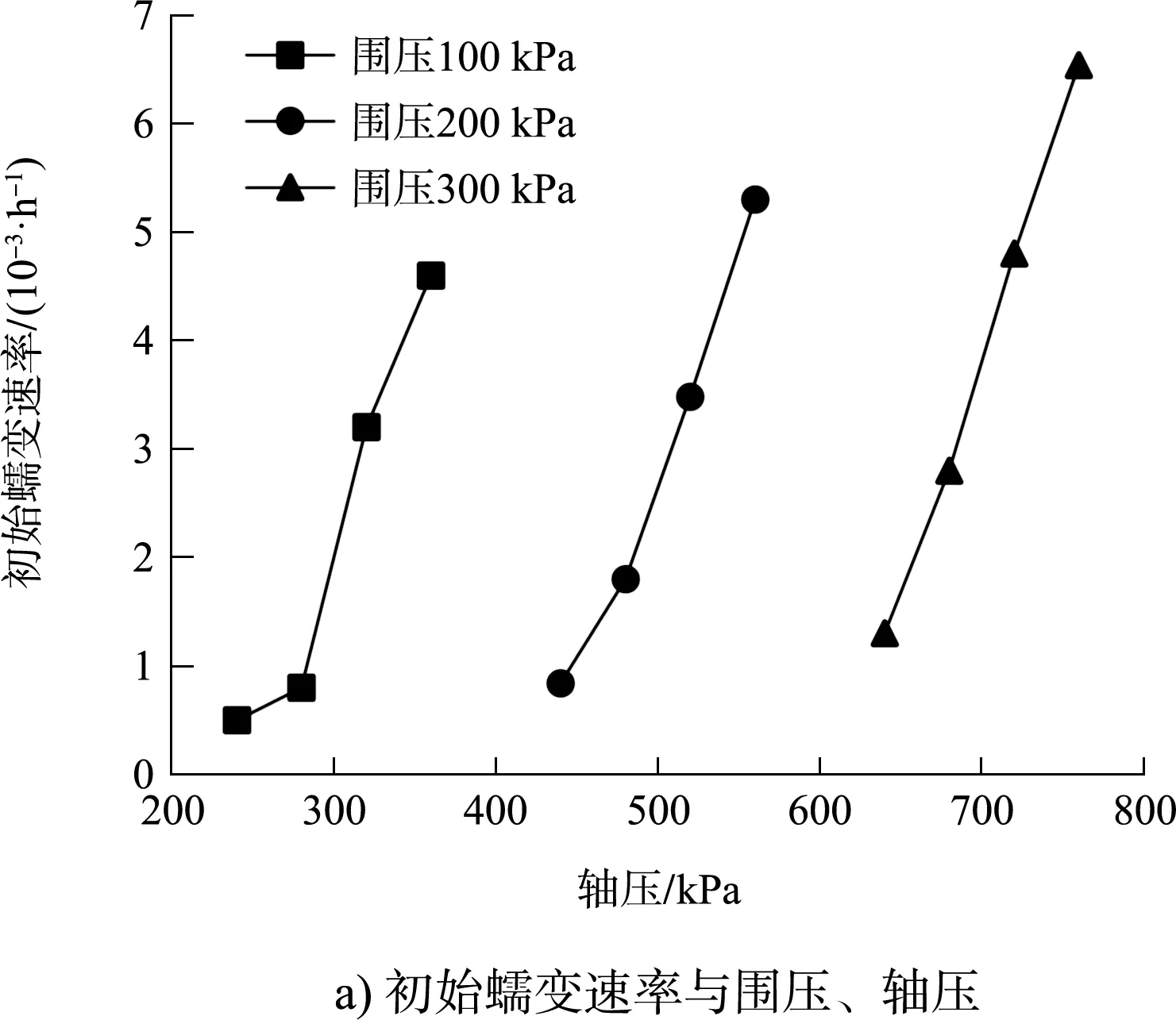
圖4 初始、穩(wěn)態(tài)蠕變速率與圍壓、軸壓關系曲線

由圖4a)可看出，在圍壓100 kPa、軸壓240 kPa下，初始蠕變速率最小，僅為0.502×10-3/h；在圍壓300 kPa、軸壓760 kPa，初始蠕變速率最大，達到6.538×10-3/h。在同一圍壓下，初始蠕變速率隨著軸壓的增大呈線性遞增趨勢。在同一加載等級下，較高軸壓和圍壓條件下初始蠕變速率始終大于較低軸壓和圍壓條件，這說明應力水平的提升會增高初始蠕變速率。由圖4b)可看出，穩(wěn)態(tài)蠕變速率與圍壓、軸壓之間的變化規(guī)律與初始蠕變速率較為相似，在圍壓100 kPa、軸壓240 kPa下，穩(wěn)態(tài)蠕變速率最小，為0.007×10-3/h；在圍壓300 kPa、軸壓760 kPa，穩(wěn)態(tài)蠕變速率最大，達到0.890×10-3/h。在同一加載等級下，較高軸壓和圍壓條件下穩(wěn)態(tài)蠕變速率始終大于較低軸壓和圍壓條件，這說明應力水平的增高使穩(wěn)態(tài)蠕變速率增大。

2.3 等時刻軸壓-軸向應變曲線

在圖2中選取0.1、10、20、30、40、50、60、70、80和90 h共10個時刻的軸壓-軸向應變數(shù)據(jù)點，繪制等時軸壓-軸向應變曲線，如圖5所示，限于篇幅，僅以淤泥質(zhì)黏土圍壓100 kPa為例。選取3種圍壓下0.1和90 h時刻的軸壓-軸向應變數(shù)據(jù)點，繪制不同圍壓下等時軸壓-軸向應變曲線，如圖6所示。

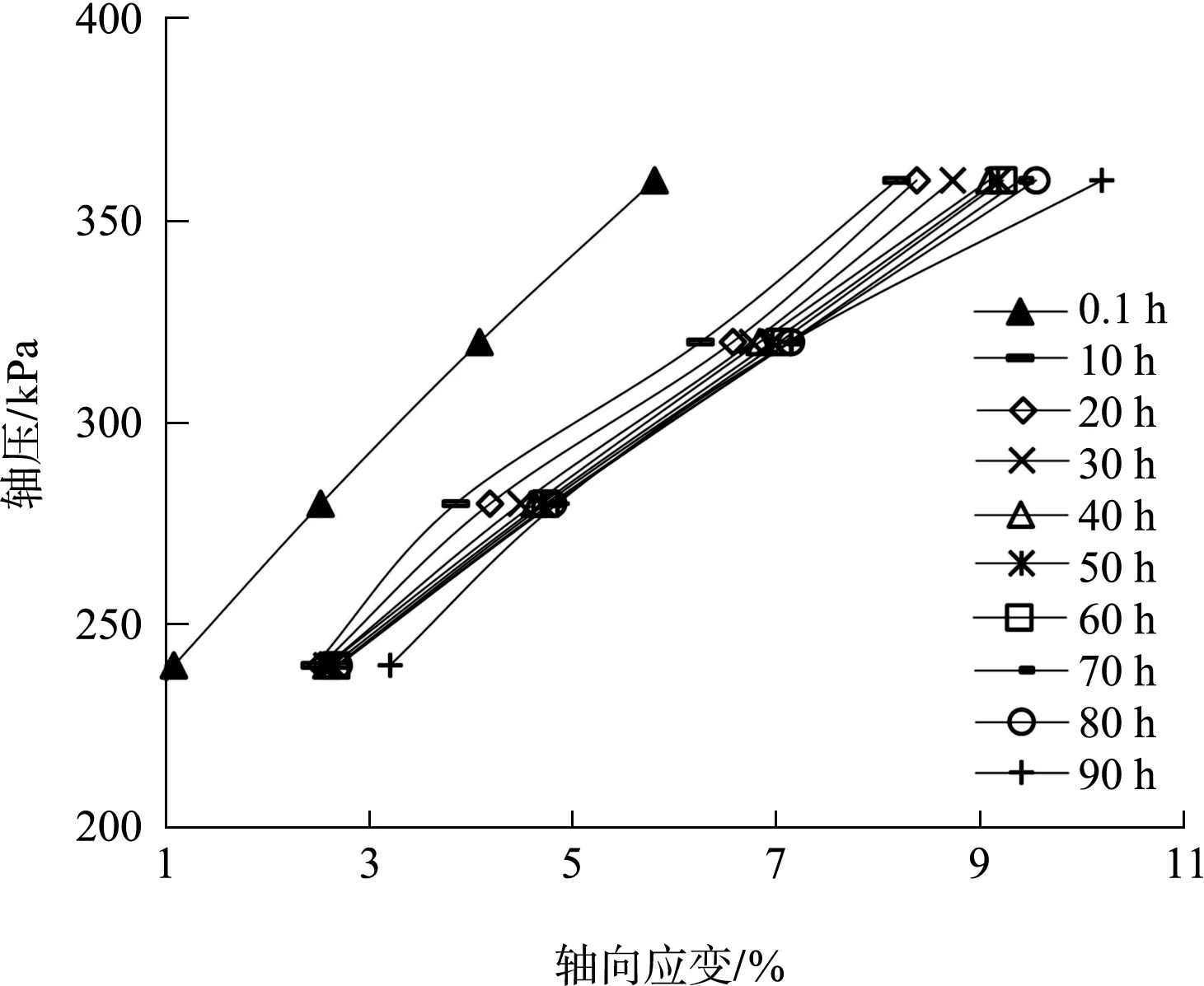
圖5 等時軸壓-軸向應變曲線

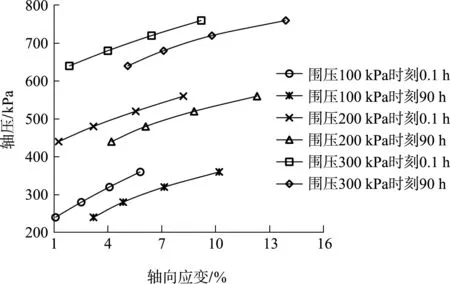
圖6 不同圍壓下的等時刻軸壓-軸向應變曲線

由圖5看出，等時軸壓-軸向應變曲線由0.1 h時刻的曲線和10～90 h曲線簇組成，0.1 h時刻的曲線近線性，10～90 h曲線簇具有明顯的非線性特征，隨著軸向應變的增長，曲線簇表現(xiàn)出逐漸靠攏應變軸的趨勢。綜合圖5、6可看出，等時軸壓-軸向應變曲線0.1 h時刻曲線近似線性，10～90 h時刻曲線簇形態(tài)近似雙曲線。

3 淤泥質(zhì)黏土蠕變經(jīng)驗模型

3.1 經(jīng)驗模型理論

目前Singh-Mitchell和Mesri經(jīng)驗模型在土體蠕變分析中應用較廣，文獻[12]在Mesri模型的基礎上改進得到Log-Modified經(jīng)驗模型。其中Mesri和Log-Modified經(jīng)驗模型的應力-應變關系式一致，均為雙曲線型，Singh-Mitchell經(jīng)驗模型的應力-應變關系式為指數(shù)型，由于Singh-Mitchell模型被證明不適用于低應力水平下蠕變行為模擬[13]，而Mesri和Log-Modified經(jīng)驗模型的應力-應變關系式與本文淤泥質(zhì)黏土等時軸壓-軸向應變較吻合，故本文分別引入Mesri和Log-Modified模型辨識淤泥質(zhì)黏土的蠕變力學行為，Mesri和Log-Modified模型本構(gòu)方程分別見式(1)(2)：

(2)

(3)

式中：ε為蠕變應變；t為蠕變時間；Eu為初始切線彈性模量；σ1為軸壓；σ3為圍壓；(σ1-σ3)f為蠕變試驗中的破壞偏應力；D為每一級加載軸壓與三軸固結(jié)排水試驗中剪切強度之間的比值；Rf為破壞比；a、b和c均為模型參數(shù)；t1為初始蠕變的參考時間，本文取t1為1 h；m為待定參數(shù)。

Mesri和Log-Modified模型共同的應力-應變關系式為：

(4)

式中：ε1為應力-應變關系中的應變。

Mesri模型的應變-時間關系式為：

(5)

Log-Modified模型的應變-時間關系式為：

ε2=(a+bt)c

(6)

式中：ε2為應變-時間關系中的應變。

兩者模型求取時，應力-應變關系參數(shù)與時間關系參數(shù)分別求解，兩者的應力-應變關系參數(shù)相同。

3.2 應力-應變關系參數(shù)求解

為了便于參數(shù)求解，變形式(4)為：

(7)

式(7)中的ε1/D與ε1線性相關，Rf為斜率，(σ1-σ3)f/Eu為截距。選取0.1～90 h共10個時刻的蠕變數(shù)據(jù)，以圍壓100 kPa為例，繪制不同時刻下ε1/D-ε1的關系曲線，如圖7所示，為觀察方便，省去部分時刻的數(shù)據(jù)。應力-應變關系參數(shù)見表3，限于篇幅，僅給出圍壓100 kPa下的參數(shù)取值。

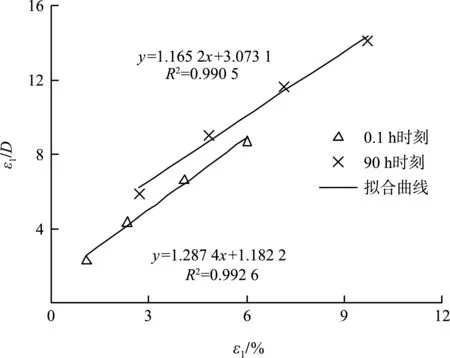
圖7 不同時刻下的ε1/D-ε1曲線

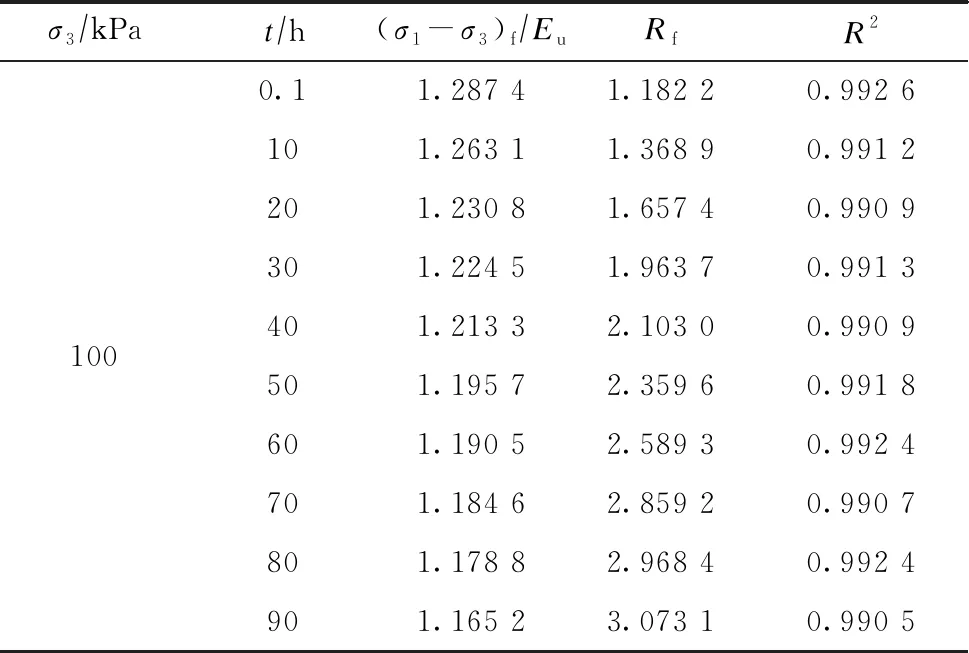
表3 應力-應變關系參數(shù)

由表3可看出，(σ1-σ3)f/Eu隨時間增長呈遞減趨勢，Rf隨時間增長呈遞增趨勢。通過式(7)線性擬合求解的方法得到不同時刻下的(σ1-σ3)f/Eu和Rf的平均值，見表4。

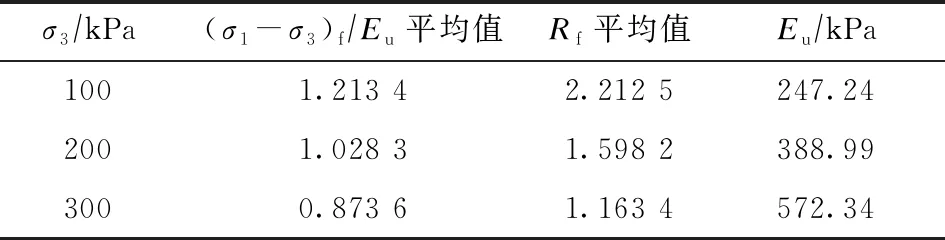
表4 應力-應變關系參數(shù)平均值

由表4可知，(σ1-σ3)f/Eu和Rf平均值均隨著圍壓增大而遞減，Eu隨著圍壓增大而遞增。

3.3 Mesri模型應變-時間關系參數(shù)求解

式(5)等號兩邊取對數(shù)可得：

lnε2=mlnt

(8)

由式(8)可看出，lnε2與lnt線性相關，m為該線段的斜率，于是繪制lnε2-lnt曲線，以圍壓100 kPa為例，如圖8所示，應變-時間關系參數(shù)見表5。

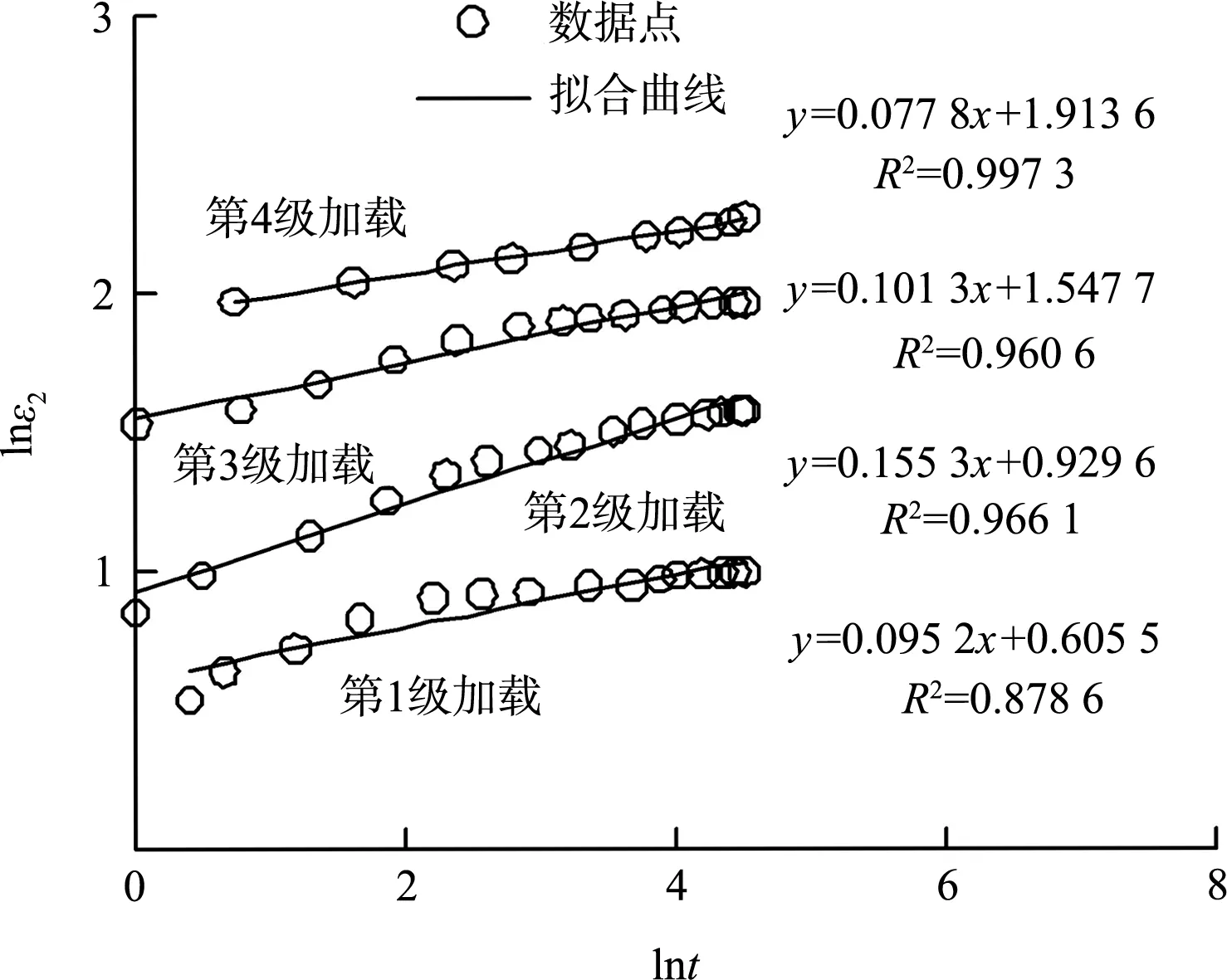
圖8 lnε2-lnt曲線

表5 Mesri模型應變-時間關系參數(shù)

由圖8可看出，lnε2-lnt線性擬合較好，R2的平均值達到0.950 7。通過式(8)線性擬合求解的方法得到不同時刻下的m的平均值，見表6。

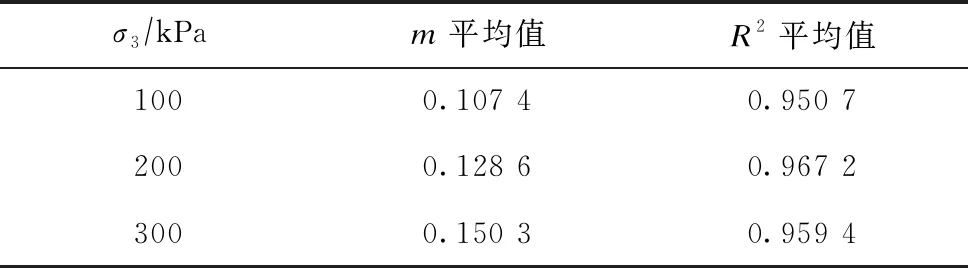
表6 參數(shù)m平均值

分析式(7)(8)發(fā)現(xiàn)，(σ1-σ3)f/Eu、Rf和m與軸壓和時間無關，均通過線性擬合求解的方法確定，故取不同加載等級下(σ1-σ3)f/Eu、Rf和m平均值作為Mesri經(jīng)驗模型參數(shù)，將表4、6中相關參數(shù)代入式(2)可得：

(9)

式(9)即為本文淤泥質(zhì)黏土在σ3=100 kPa下的Mesri蠕變經(jīng)驗模型。

3.4 Log-Modified模型應變-時間關系參數(shù)求解

通過數(shù)學軟件Origin對圖2蠕變數(shù)據(jù)進行擬合，算法采用一般的非線性最小二乘法，取參數(shù)a、b和c的平均值見表7。

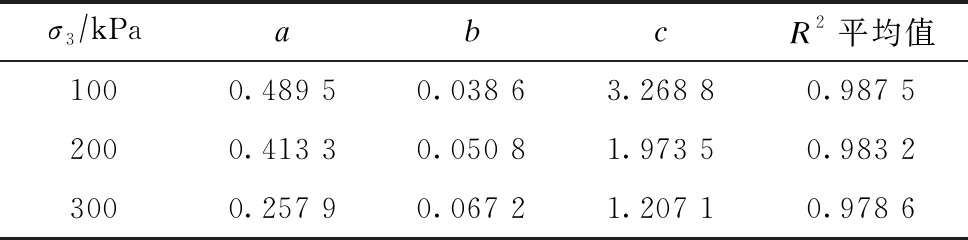
表7 參數(shù)a、b和c平均值

將表7中參數(shù)a、b和c的平均值及表4中(σ1-σ3)f/Eu和Rf平均值代入式(3)可得：

(10)

式(10)即為本文淤泥質(zhì)黏土在σ3=100 kPa下的Log-Modified蠕變經(jīng)驗模型。

4 模型參數(shù)求解及驗證

以σ3為100和300 kPa的試驗數(shù)據(jù)為例，對本文Mesri和Log-Modified蠕變經(jīng)驗模型進行對比模擬驗證，經(jīng)驗值與試驗值對比曲線如圖9所示。

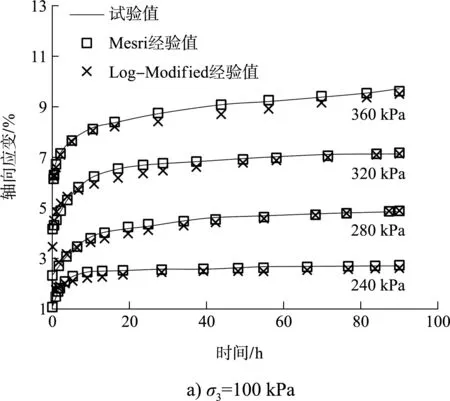
圖9 經(jīng)驗值和試驗值對比曲線

由圖9可看出，Mesri蠕變經(jīng)驗模型辨識能力較強，擬合精度較高，R2平均值為0.990 5，而Log-Modified蠕變經(jīng)驗模型的經(jīng)驗值總體上低于試驗值，擬合效果一般，R2平均值為0.954 7。工程實踐中，若采用Log-Modified蠕變經(jīng)驗模型預測計算淤泥質(zhì)黏土地基長期沉降及穩(wěn)定性，在更長時限范圍內(nèi)，可能會造成較大誤差，造成潛在的安全隱患。Mesri蠕變經(jīng)驗模型能較好地描述本文淤泥質(zhì)黏土蠕變特性，將其作為本文淤泥質(zhì)黏土的推薦模型。

5 結(jié)論

1)本文開展淤泥質(zhì)黏土固結(jié)排水三軸壓縮蠕變試驗，淤泥質(zhì)黏土在加載時瞬間彈性變形，隨后依次進入衰減、穩(wěn)定蠕變階段。同一圍壓下，隨著軸壓的提升，軸向應變逐漸遞增。同一加載等級下，圍壓和軸壓的升高促進軸向應變的增長。

2)在同一圍壓下，隨著加載等級的提升，淤泥質(zhì)黏土初始蠕變速率和穩(wěn)態(tài)蠕變速率均呈線性遞增趨勢。在同一加載等級下，較高軸壓和圍壓條件下初始、穩(wěn)態(tài)蠕變速率均始終大于較低軸壓和圍壓條件。淤泥質(zhì)黏土等時軸壓-軸向應變曲線近似雙曲線，具有明顯的非線性特征，隨著軸向應變的增長，曲線簇表現(xiàn)出逐漸靠攏應變軸的趨勢。

3)結(jié)合淤泥質(zhì)黏土的等時軸壓-軸向應變雙曲線形態(tài)特征，分別引入Mesri和Log-Modified模型來辨識蠕變數(shù)據(jù)，給出兩者模型參數(shù)求解方法，得到適用于本文淤泥質(zhì)黏土的Mesri和Log-Modified蠕變經(jīng)驗模型，通過對比發(fā)現(xiàn)Mesri蠕變經(jīng)驗模型辨識效果優(yōu)于Log-Modified蠕變經(jīng)驗模型，R2平均值達到0.990 5，將Mesri蠕變經(jīng)驗模型作為本文淤泥質(zhì)黏土的推薦模型。