爆破振動對臨近隧洞襯砌結構的影響和施工建議

黃 丹

(朝陽市江河流域保護管理局，遼寧 朝陽 122000)

1 工程背景

清河水庫為遼寧省遼河干流上的重要防洪控制性工程，不僅承擔著清河、遼河的錯峰任務，還擔負灌溉、供水、養殖等諸多任務，屬于多年調節大(2)型水利樞紐工程。水庫的總庫容為9.68億m3[1]。泄洪洞位于水庫大壩的右岸，為圓形有壓隧洞設計，洞徑為4.0m。在水庫除險加固工程建設中，結合水庫供水取水頭部和輸水改造工程建設，需要自調壓井至出口新建一條洞徑4.0m，長115.67m的泄洪洞[2]。受到大壩右岸地形和地質特點的限制，新建泄洪洞需要避開大壩右岸山體中的F031斷層破碎帶，因此新建泄洪洞和原泄洪洞之間的凈距較小。在新泄洪洞爆破開挖過程中，爆破振動勢必會對原泄洪洞的襯砌結構安全穩定性造成一定的影響[3]。本研究通過數值模擬的方式，探討不同情況下爆破振動對臨近泄洪洞襯砌結構的影響并提出相應的設計和施工建議，以保證施工的順利進行。

2 ANSYS/LS-DYNA有限元模型

2.1 軟件選擇

ANSYS/LS-DYNA軟件可以進行幾何、材料、接觸等領域的非線性分析，其程序內部包含了Lagrange、ALE和Euler算法，不僅可以進行顯式求解，亦可以進行隱式求解；不僅可以進行靜力分析，亦可以進行線性動力分析。該軟件在爆破沖擊、高速撞擊以及金屬鍛造成型領域具有成熟的應用，十分適合本研究需求[4]。基于此，本研究選擇ANSYS/LS-DYNA進行有限元計算模型的構建。

2.2 模型的構建

根據相關研究成果，在爆破開挖施工過程中，影響爆破振動衰減規律的主要因素是隧洞圍巖的性質，因此在模型構建過程中可以對隧洞的支護結構進行必要的簡化[5]。在幾何模型構建方面，以垂直于隧洞中線指向右側的方向為X軸正方向，以豎直向上的方向為Y軸正方向，以開挖方向的反方向為Z軸的正方向。根據圣維南原理，在大于開挖洞徑3倍的范圍之外，其邊界效應可以忽略不計。由此確定X、Y軸方向的計算范圍為25m，Z軸方向長30m。巖體和混凝土結構采用Lagrange網格建模，空氣和炸藥采用ALE網格建模，在模型網格剖分過程中，使用solid- 164八節點六面體單元。

2.3 邊界條件和計算參數

在爆破開挖問題的數值模擬研究過程中，如果采用傳統的結點固定方式對邊界問題進行處理，會造成計算過程中應力波和反射波之間的相互疊加，進而影響求解的效率和精度[6]。如果采用增加模型尺寸的方式延遲波的反射時間，則會造成計算效率的大幅降低。因此，在模型計算過程中采用無反射邊界條件[7]。該邊界條件的原理是安置一種基于有限域的人為阻尼邊界條件，隔離出一個特定的區域保證應力波和反射波的能量能夠由近至遠輻射出去，并避免波的能量在有限范圍內集中[8]。

根據前期的地質勘查資料，隧洞圍巖為花崗巖，結合采樣測定和查閱相關文獻，確定模型參數，見表1。

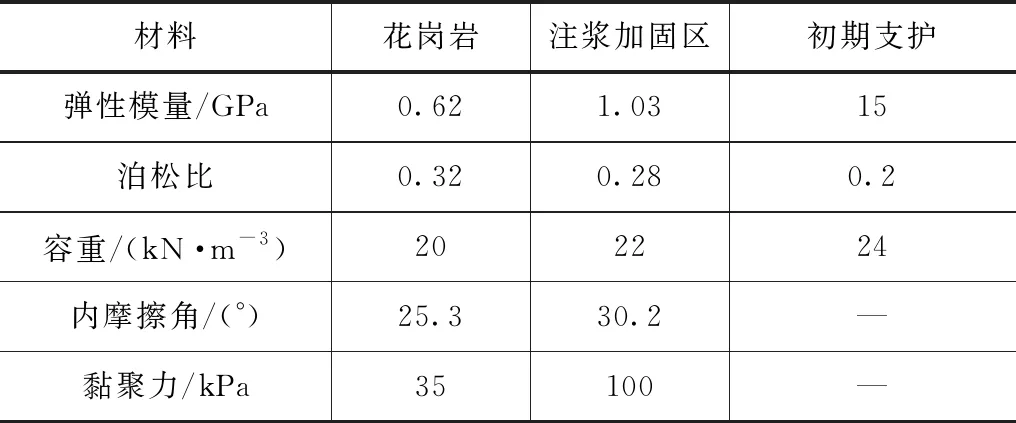
表1 模型材料參數

2.4 計算方法

在模型計算過程中，對隧洞圍巖的巖石材料采用各向同性的塑性動力模型進行描述。在襯砌結構數值模擬中選擇H-J-C本構模型，在顯式中心差分法下，幾何尺寸最小的單元控制著模型計算的時間步長。因此，需要在LS-DYNA程序中使用質量縮放，從而實現對每個單元密度的有效控制，最終達到合適的模型計算時間步長。在ANSYS/LS-DYNA軟件中，提供了可以用于爆破問題數值模擬的3種常用算法，分別為Lagrange算法、Euler算法和ALE算法。這3種算法各有優劣：Lagrange算法能夠對結構的邊界運動特征進行準確描述，具有較高的計算效率，但是面臨結構大變形時，容易造成網格單元的畸變，從而顯著影響計算精度，Euler、ALE算法雖然比較適合大變形問題的求解和計算，但是計算的復雜程度有所提高，計算效率相對偏低，綜合上述3種算法的優缺點，本研究選擇流-固耦合模型算法。

3 計算結果與分析

3.1 間距的影響

顯然，隧洞之間的間距是爆破振動影響的主要因素，以Ⅲ級圍巖為例，模擬計算保持其余參數的原始設計值不變，確定2個隧洞之間的凈距為20、25、30、35和40m等5種不同的數值，利用構建的有限元模型進行模擬計算，獲得隧洞拱頂和拱腰部位的振速和位移值。并繪制出振速和位移隨隧洞間距的變化曲線，結果分別如圖1—2所示。

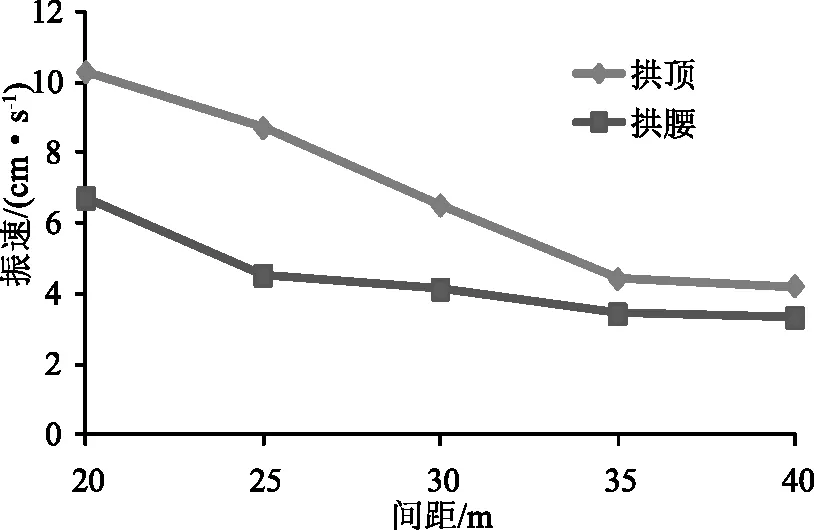
圖1 振速隨隧洞間距變化曲線

圖2 位移隨隧洞間距變化曲線

由圖1可以看出，襯砌結構的最大振速隨著隧洞間距的增大而減小，并逐漸趨于穩定的變化特點，且拱頂部位的振速大于拱腰部位的振速。在間距相同的情況下，拱頂部位振速值約為拱腰部位的1.4倍左右。從具體數值來看，當隧洞間距小于30m時，拱頂部位的最大振速值均大于7.0cm/s的工程設計值，特別是間距為20m時最大振速達到10.2cm/s，超過工程設計值的40%，存在較大的施工安全隱患。由圖2可以看出，拱頂和拱腰的位移值隨著間距的增大而波動減小，并在間距大于35m時基本趨于穩定。但是，總體來看，圍巖在爆破振動作用下的位移量較小，不會對施工安全造成顯著影響。綜合振速和位移的計算結果，在工程設計時，2個隧洞的最小間距以35m為宜。

3.2 圍巖等級

圍巖等級是影響工程施工參數確定的重要因素，由于背景工程的地質環境比較復雜，隧洞設計線路上存在Ⅱ級、Ⅲ級和Ⅳ級圍巖洞段。因此，研究中調整圍巖參數，模擬計算不同級別圍巖不同間距條件下隧洞拱頂襯砌部位的振速，計算結果見表2。

由表2中的數據可以看出，圍巖等級對爆破振動條件下拱頂部位的振速值產生比較顯著的影響，在相同間距條件下，圍巖的等級越低振速值就越大。當時，就背景工程而言，當隧洞間距為35m時，拱頂部位的振速值均小于工程設計值，不會對工程的施工安全和原泄洪洞襯砌結構的安全穩定性造成影響。因此，在工程設計過程中，整個線路的間距不小于35m即可。但是在Ⅳ級圍巖情況下，間距35m時的振速值偏大，為5.54cm/s。為了確保共工程的安全性，在施工過程中要加強爆破振速的監測，一旦出現超標現象，應該立即采取措施。

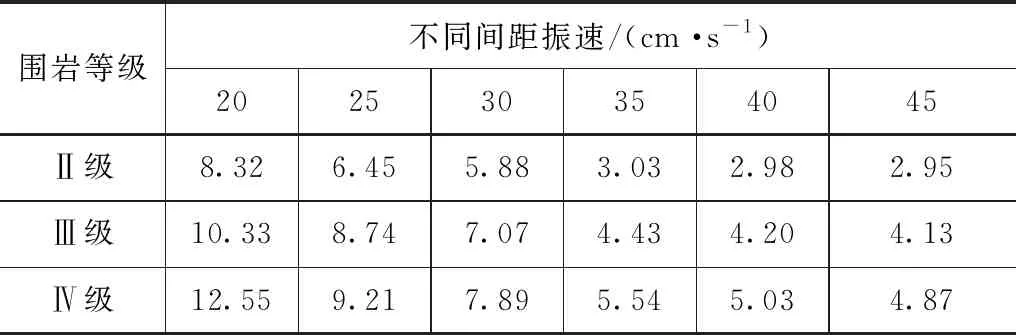
表2 不同圍巖級別振速計算結果

3.3 裝藥量

在地下洞室工程爆破開挖過程中，需要利用炸藥的瞬間的物理化學變化釋放的能量，使隧洞掌子面的圍巖破碎。因此，裝藥量的大小必然會對爆破效果造成顯著影響。在具體的施工過程中，增加裝藥量可以有效降低施工成本，但是也會造成圍巖和襯砌結構的強烈震動。在具體的施工設計過程中，需要對施工效率、工程成本和安全性進行綜合考慮，以確定最佳裝藥量。在此次研究中，保持2個隧洞的間距為35m不變，設置原始裝藥量的0.9、1.0、1.1、1.2和1.3倍等5種不同的裝藥量方案，對Ⅳ級圍巖等級的拱頂振速進行模擬計算，結果如圖3所示。

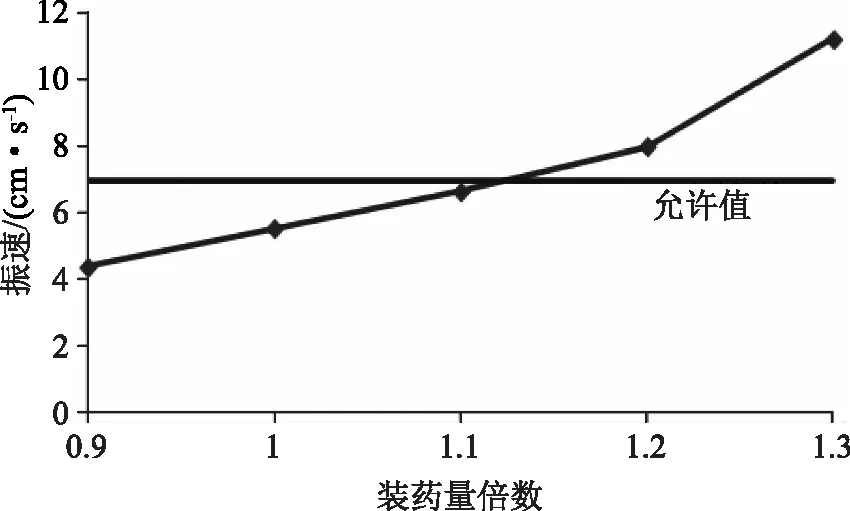
圖3 拱頂振速隨裝藥量倍數變化曲線

由圖3可以看出，隧洞拱頂襯砌部位的振速隨著裝藥量的增加呈現不斷增加的變化特點，裝藥量越大，結構的振速值也就越大。從具體計算結果來看，當裝藥量為原設計方案的1.1倍時，其對應的振速值略小于允許值。因此在施工中可以將裝藥量提升至原來的1.1倍。當然，在施工過程中應該加強振速監測，保證施工的安全進行。

4 結論

此次研究以清河水庫右岸新建泄洪洞為例，探討了爆破開挖振動對原有泄洪洞襯砌結構的影響，獲得的主要結論如下。

(1)襯砌結構的最大振速隨著隧洞間距的增大而減小，并在大于35m的情況下趨于穩定，且拱頂部位的振速大于拱腰部位的振速。

(2)在相同間距條件下，圍巖的等級越低振速值就越大；當隧洞間距為35m時，3種圍巖等級的拱頂部位的振速值均小于工程設計值。

(3)隧洞拱頂襯砌部位的振速隨著裝藥量的增加呈現不斷增加的變化特點，當裝藥量為原設計方案的1.1倍時，其對應的振速值略小于允許值。

(4)根據研究結果，建議在工程設計中隧洞間距不小于35m；裝藥量可以增加至原方案的1.2倍。