直升機場建設過程中方格網法土方量計算模型研究
陶彬 夏露 王思揚
(中國人民解放軍陸軍航空兵學院,北京 101116)
土方量是機場選址建設階段必須考慮因素。選堪階段,通過在地形圖上快速測定直升機場預設地域的土方量,能夠快速確定直升機場的工程進度,方便指揮員指揮重型工程機械開展機場場址建設作業,為指揮決策提供準確數據。在工程項目上,精確的土方量計算直接影響場址建設進度,有時還會引起相關各方的經濟糾紛。本文針對直升機場開辟過程中對場地的整平要求,開展土方量計算研究,設計直升機場開辟過程中的土方量計算模型。基于Matlab/Simulink 數字化建模軟件,對土方量計算模型進行建模,實現土方量的快速運算。
1 直升機場對地勢的要求
直升機場有一定的跑道長度、停機坪數量,平整度是場道表面評價的一個重要參數。不同等級的直升機場場道平面都有嚴格標準,而實際建設中存在一定的偏差,我們把這種偏差叫做平整度。平整度非常關鍵直接影響直升機的滑行動力、跑道承受力,因而直接影響飛行質量。在機場建設管理中,用機場跑道面上的凹凸部分表征場道的不平整度。而地勢的整平對場道平整度建設有直接聯系,因此,良好的平整度需要精準的地勢整平作業,精準的土方量計算。
1.1 直升機場平整度要求
為了滿足飛機的使用要求,水泥混凝土道面平整度允許值是有一定的上限的。在實際操作中,采用直尺法來衡量平整度,在一定范圍內,通過直尺與地面的間隙來確定平整度。因此,專用的場道直尺就是測量工具,根據有無支腳,工具可以劃分為兩種,有支腳、無支腳,根據長度劃分,市面上有3m、4m、5m 等不同規格,我國民用機場等場所測量平整度普遍采用3m 長的直尺。
直升機場平整度要求,如下:
1.1.1 在水泥混凝土到面上,3m 長的測量尺與測定區域接觸部位,中間空隙值長度在3mm 以內。在500m 的范圍中,檢查區域不少于2 塊水泥混凝土道面板。水泥混凝土道面需要測量兩塊水泥板對角線,然后取2 組對角線的間隙的最大值然后進行平均,作為測量值。
1.1.2 高差允許值,相鄰兩塊水泥板縱向連接處的高差值在3mm 以內,橫向連接處的高差值在2mm 范圍內。縱向縫隙需要在50m 范圍內至少檢查1 點,橫向縫隙需要每10條抽查檢驗1 條,再檢查點的數量上,要求1~2 點。
1.1.3 單塊水泥混凝土板設計與實際安裝偏差在±5mm范圍內。
1.1.4 坡度標準,以直升機軸線方向為標準,為起落坪、停機坪垂直于標準方向的坡度在1.5%范圍內,平行于標準方向的坡度在0.8%范圍內,在平行、垂直方向上,要確保一個方向的坡度不小于0.5%,同時要滿足凈空環境以及其他要求。
1.2 保障場地對地勢平整度的要求
直升機場保障場地,主要承受各種工程車輛行駛、承載作用。保障場地的平整度直接影響保障車輛的行駛效率、質量。不平整的保障場地會增大行車阻力、迫使保障車輛振動,影響行車的速度和安全,影響駕駛的平穩,增加對保障場地路面沖擊和汽車機件的損壞等一系列不良影響.另外,不平整的保障場地還會引發保障場地大面積積水,從而引發保障場地出現塌方等損害。因此,為減少上述災害、損害的發生,要嚴格要求保障場地的平整度問題。在地勢整平過程中參照直升機場平整度標準,開展整平工作。
2 直升機場土方量計算方法選擇
直升機場地面平坦或起伏較小的一個較大區域,其最主要特點就是平坦寬廣,起伏較小。實際上,直升機場開設的區域,一般較為平坦,微地貌相對簡單,但是地面常常會出現起伏,在區域范圍內高差在1m 左右,有機場建設區域地形地勢限制,一般在此區域內一般沒有等高線。
而方格網法其基本原理是找到等高線,在機場建設區域,進行劃分網格,針對劃分的網格分別測量出每個網格中各個典型代表點的高程,然后估算出內個網格的平均高程。根據機場各個網格平均高程和機場規劃場道要求坡度,確定機場建設區域的填土區域和挖土區域,進一步確定填挖邊界線。機場建設區面積也符合網格法對測量面積的需要。應用方格網法開展機場建設土方量計算具有簡明直觀、通用性強,土方量預算相對準確等特點。
2.1 方格網法土方量計算研究
方格網法將要土方量計算區域劃分網格,根據要設計高程以及該區域實際位置高程確定土方的填挖量,最后將填、挖方量累計求和。該方法首先利用方格的四個角的高程求出該方格的平均高程,然后依據設計高程,計算出差值,進而得到此方格的土方量填、挖量,總的土方量等于各方格土方量的和:

式中:Hij表示第i 行j 列的方格網的高差;a,b為方格網邊長;n 為測區方格的個數。
2.2 方格網法計算案例分析
2.2.1 打方格網
打方格網是方格網法的關鍵,首先確定方格的長度,一般取10m、20m、50m 的長度作為基準。其大小要以實際計算土方量的地形復雜程度、比例尺的精度等因素來確定。每個方格點的地面高程可以根據比例尺地形圖圖上作業求得,標注在圖上。(如圖1 所示),本文所選取案例取方格邊長20m。

圖1 方格網法計算原理圖
2.2.2 計算設計高程
每個方格網的高程根據四個頂點的高程求平均值得到。按照此種方法進行遞推,再根據方格數,把所有求得的方格平均高程求和,再除以方格的數量,這就是設計高程。

式中Hi為每一方格的平均高程;n 為方格總數。
根據我們計算出來的設計高程的值與每個方格計算的高程值進行比較、計算,分別確定出每個方格的填、挖土方量的值。從求解過程,可以看出網格法求土方量計算工作較大。
通過對土方量設計高程計算過程的研究可以看出:角點A1、A4、B5、E1、E5的高程在計算過程中只是使用過1 次,邊點A2、A3、B1、D1...等點的高程在計算過程中使用過2 次,拐點B4的高程使用更加多,3 次,其他的中間點B2、B3、C2、C3...的高程在計算中用過四次,這樣,通過上述分析,可以得到設計高程表達式如下。

式中n 為方格總數。
用公式(3)進行土方量估算,其設計高程為64.84m,這就是此區域的填挖分界線。
2.2.3 計算方格頂點的填挖高度
根據設計高程和方格頂點的地面高程,計算每一方格頂點的挖、填高度。

將計算好的挖、填高度標注在相應方格頂點的右下方,“+”號為挖,“-”號為填。
2.2.4 計算填、挖土方量
填、挖土方量(角點土方量V角,邊點土方量V邊,拐點土方量V拐,中點土方量V中)分別按下式計算

式中:h- 各方格頂點的填、挖高度;P格- 方格內面積;V- 填、挖土方量。
由圖2 可知,11 個挖方方格頂點,13 個填方方格頂點,通過分別列表的方式開展計算。

圖2 方格網法填方模型
3 Matlab/Simulink 方格網法土方量建模研究
Matlab 是一種數學集合模塊化軟件,包含多種集成的數學模塊,該軟件提供如下建模功能,編輯器、命令窗口、調試器、簡單的編程環境、完備的調試系統,程序經過模塊化處理可以直接運行,并用運行自檢功能,發現問題系統會自動提示問題原因。
Simulink 是Matlab 軟件中的一個較大模塊,它具有設計、仿真、生成代碼、連續測試和驗證等功能。Simulink 尤其具有以下個性功能,圖形編輯、可自定義模塊庫、求解、動態系統建模和仿真。
3.1 數據來源
數據來源圖1,實際測量中可以使用儀器獲得高程數據。

表1 方格網法原始數據
3.2 明確變量參數
明確變量參數,顯然下面的量是需要考慮的:
方格網各頂點的高程,用Hi記;
方格頂點的類別(即計算方格頂點的高差所占的權重),用Ki 記,設角點的權重為1,邊點的權重為2,拐點的權重為3,中(間)點的權重為4;
設方格網總數n=15;
選用方格網的邊長,設b=20m,則單個方格網的面積P格=b2=400m2;
3.3 數據處理
若H0記設計高程,則H0=(∑H角+2∑H邊+3∑H拐+4∑H中)÷4×15=64.84m;
若用hi記單個方格頂點的填挖高差hi=Hi-H0;則填挖土方量Vi=hi×Ki×P格:
A1 +204 B5 -48 D3 -188 A2 +250 C1 +216 D4 -292 A3 +124 C2 +176 D5 -202 A4 +33 C3 -84 E1 -20 B1 +302 C4 -204 E2 -120 B2 +324 C5 -142 E3 -192 B3 +120 D1 +106 E4 -206 B4 -27 D2 +20 E5 -126
將表2 中的填挖方量按正負分開統計得表3。

表2 填挖土方量

表3 填挖方量(改)
此即為方格頂點的填、挖高值×方格頂點的類別(權重)×方格網的面積的四分之一的結果。對算出的填、挖方量分別進行積分,即可得到總填、挖方量的結果。并通過示波器顯示出計算的過程。
3.4 建立模型
其中名為“方格頂點的填高值”的From Spreadsheet 模塊選取的數據范圍是表3 中E2-E14 的數據,名為“方格頂點的類別”的From Spreadsheet 模塊選取的數據范圍是表3中F2-F14 的數據,值為400 的Constant 模塊名為“方格網的面積”與倍率為0.25 的Gain 模塊相連,代表四分之一的方格網的面積。方格頂點的填高值、方格頂點的類別與四分之一的方格網面積的乘積Product 即為單個方格網頂點的填方量,而后連接Integrator 對其進行積分,得到總填方量。
最后結果在Display 模塊中顯示出來,并在Scope 模塊中呈現出積分過程。橫坐標表示總共進行了13 次積分運算,縱坐標表示每次積分的運算結果。最后的總填土方量為1851m3。
其中名為“方格頂點的挖高值”的From Spreadsheet 模塊選取的數據范圍是表3 中B2-B12 的數據,名為“方格頂點的類別”的From Spreadsheet 模塊選取的數據范圍是表3中C2-C12 的數據,值為400 的Constant 模塊名為“方格網的面積”與倍率為0.25 的Gain 模塊相連,代表四分之一的方格網的面積。方格頂點的挖高值、方格頂點的類別與四分之一的方格網面積的乘積Product 即為單個方格網頂點的挖方量,而后連接Integrator 對其進行積分,得到總挖方量。最后結果在Display 模塊中顯示出來,并在Scope 模塊中呈現出積分過程。
最后結果在Display 模塊中顯示出來,并在Sc ope 模塊中呈現出積分過程。橫坐標表示總共進行了11 次積分運算,縱坐標表示每次積分的運算結果。最后的總挖土方量為1875m3。
如圖2 與圖3 所示,總挖方量為1875m3,總填方量為1851m3。總填方量和總挖方量在理論上應相等,但因為存在測量和計算誤差,兩者總有些出入。為了求得填、挖土方量相等或相近,需要多次調整設計高程,計算填、挖土方量。
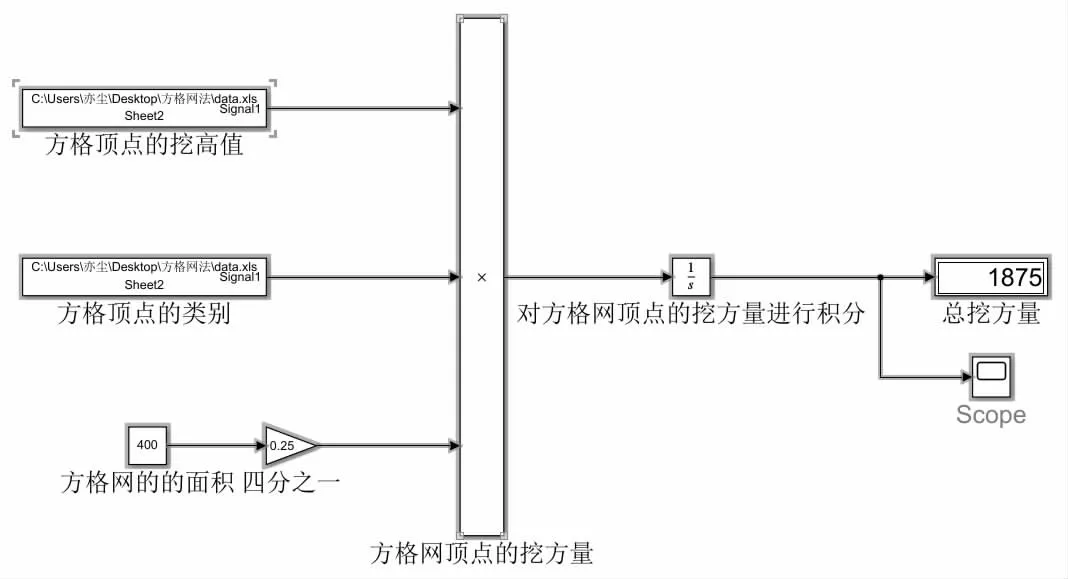
圖3 方格網法挖方模型
4 結論
方格網法適用于在等高線稀疏的平原地區以及較為平緩的山地進行的工程的土方量的計算。基于Matlab/Simulink應用方格網法開展土方量建模,在一定范圍內能夠快速、合理模擬計算出土方量計算填、挖土方量,模擬算出的填挖方量基本相等,滿足填挖方平衡的要求。在直升機場開辟建設過程中能夠快速、準確的模擬計算出場地的土方量填、挖量,所模擬計算數據能夠對工程開展提供一定的指導。

