Buckling analysis of shear deformable composite conical shells reinforced by CNTs subjected to combined loading on the two-parameter elastic foundation

A.H.Sofiyev , N.Kuruoglu

a Department of Civil Engineering of Engineering Faculty, Suleyman Demirel University, 32260, Isparta, Turkey

b Information Technology Research and Application Center Member of Consultancy Board of ITRAC Center, Istanbul Commerce University, Beyoglu, 34445,Istanbul, Turkey

c Scientific Research Centers for Composition Materials of UNEC-Azerbaijan State Economic University,1001/Baku, Azerbaijan

d Department of Civil Engineering of Faculty of Engineering and Architecture of Istanbul Gelisim University, Istanbul, Turkey

Keywords:Nanocomposites CNTs Composite conical shells Two-parameter elastic foundations Combined buckling loads Shear deformation shell theories

ABSTRACTThe main objective of this study is to investigate the buckling analysis of CCSs reinforced by CNTs subjected to combined loading of hydrostatic pressure and axial compression resting on the twoparameter elastic foundation (T-P-EF).It is one of the first attempts to derive the governing equations of the CCSs reinforced with CNTs, based on a generalized first-order shear deformation shell theory(FSDST)which includes shell-foundation interaction.By adopting the extended mixing rule,the effective material properties of CCSs reinforced by CNTs with linear distributions are approximated by introducing some efficiency parameters.Three carbon nanotube distribution in the matrix, i.e.uniform distribution(U) and V and X-types linear distribution are taken into account.The stability equations are solved by using the Galerkin procedure to determine the combined buckling loads (CBLs) of the structure selected here.The numerical illustrations cover CBLs characteristics of CCSs reinforced by CNTs in the presence of the T-P-EF.Finally,a parametric study is carried out to study the influences of the foundation parameters,the volume fraction of carbon nanotubes and the types of reinforcement on the CBLs.

1.Introduction

The importance of shell theories in modern science and technology is growing every day.While the theory of plates and shells solves the rational tasks of designing engineering structures,which consisted mainly of finished materials, at the present time, the optimal design and production of the materials that make up the structures play a more active role.Recently, using new technological methods, developing the properties of the various materials that make up the structural elements,designs are created with high performance and low cost [1,2].

Due to its high aspect ratio, large surface area, rich surface chemical functionality and nanoscale dimensional stability, CNTs have various applications such as electromagnetic interference protection, membranes and structural reinforcement.CNTs have the simplest chemical composition and atomic bonding configuration, adding extraordinary variety and richness in the properties of the structures.The CNTs were discovered by Sumio Iijima in 1991, shortly after the laboratory synthesis of fuller in the installation of the arc discharge apparatus [3].

In modern technology, there is a need for lightweight, flexible and durable alternatives to replace hard and brittle materials.Instead of traditional materials that have been used for thousands of years, synthetic materials today can be produced at the scale of atoms, including CNTs.The nanotubes are a structural element made by bending graphene, which consists of one row of carbon atoms, into a cylinder.Even though it has such a simple shape, it becomes more effective as its physical and chemical properties change as the length and diameter change.The carbon nanotubes,which can reach a diameter of millions of times,are more beneficial than other materials due to their properties such as strength,electrical conductivity, and thermal conductivity [4,5].

The superior properties of CNTs open up exciting possibilities for new composites.NASA has invested heavily in the development of carbon nanotube-based composites for applications such as a mission to Mars.Recently, polymer/CNT composites have received great attention due to their unique mechanical, surface and multifunctional properties, as well as their strong interaction with the matrix due to their nanoscale microstructure and extremely large interfaces [6].Determination of thermal, electrical and mechanical properties of composites reinforced with carbon nanotubes reveals the extraordinary advantages of nanocomposites.Velasco-Santos et al.[7]investigated the effect of multi-walled carbon nanotubes (MWCNTs) and processing methods on the morphological, dynamic, mechanical, mechanical, thermal and electrical properties of MWCNT/nylon 6 (PA6) composites.Moniruzzaman and Winey [8]summarized various nanotube/polymer composite manufacturing methods, including solution mixing,melt mixing,and in-situ polymerization,with special emphasis on evaluating the dispersion state of nanotubes.In addition, mechanical, electrical, rheological, thermal, and flammability are specifically discussed,and the variation of these physical properties depending on the size,aspect ratio,loading,distribution status and alignment of nanotubes in polymer nanocomposites is discussed.Alizada and Sofiyev [9]created modified Young’s moduli of nanomaterials taking into account the scale effects and vacancies.Díez-Pascual et al.[10]presented research on the production of single-walled carbon nanotube buckypaper reinforced poly (phenylene sulphide) and poly (ether-ether ketone) composite laminates by hot press process using transmission electron microscopes.

The advent and widespread use of carbon nanotubes led to the development of new generation heterogeneous composite structures based on polymers.The defense industry is undoubtedly one of the earliest manufacturers of advanced composites,in particular CNT-reinforced composites.This is due to the fact that the defense industry requires materials with low weight, high strength and stiffness.The composite circular shells reinforced by CNTs,combining lightness with high strength are widely used in many branches of the modern defense industry, such as submarines,aircraft and spaceships, rockets, pressure vessels, for military drones,armored military vehicles,etc.,and are subjected to various combined loads.It is of great technical importance to clarify the buckling behavior of heterogeneous composite shells under combined loadings.Although not many, there are some remarkable studies on this problem.The buckling problem of heterogenous composite cylindrical shells reinforced with carbon nanotubes under combined loads was first mathematically modeled and solved in the study of Shen and Xiang [11].After this study, the stability problems of rotating cylindrical shells reinforced by CNTs and nano-shells under combined loadings were solved in various formulations[12,13].Later Sofiyev et al.[14]presented a solution to the problem of stability of composite conical shells reinforced with carbon nanotubes under combined loads.

Due to structural elements reinforced by CNTs are used in a variety of environments, the influence of elastic media on their behavior is crucial for safety.One of the more frequently used models that better define the structure of elastic foundations is the two-parameter elastic foundation model or Pasternak model [15].The special case of the Pasternak model is the one-parameter elastic foundation model or Winkler elastic foundation model(W-EF),which is defined as a system of parallel springs that do not touch each other [16].In addition to these models, basic information about other foundation models and their interactions with structural members are also presented in Ref.[17].The interaction of the homogeneous conical shells with the two-parameter elastic foundation (T-P-EF) and the solution of bending problems suggested by Sun and Huang [18].

The use of advanced composites in unmanned aerial vehicles,armor of tanks and aircraft, wing and empennage elements of aircraft and runways, especially on ships, submarines and oil transportation, makes a significant contribution to the development of various industries, including the defense industry.Since 2014,research has been conducted on the stability and vibrational characteristics of structural elements reinforced with CNTs resting on the EFs.For example,the influence of the two-parameter elastic foundation on the buckling or vibration behaviors of the composite plates and panels reinforced with carbon nanotubes has been studied in various formulations and theories.Zhang et al.[19]studied vibration for functionally graded carbon nanotubereinforced composite thick plates resting on elastic foundations using the element-free IMLS-Ritz method.Fu et al.[20]analyzed the nonlinear dynamic stability of carbon nanotube-reinforced composite plates resting on elastic foundations.Bani’c et al.[21]examined influence of Winkler-Pasternak foundation on the vibrational behavior of plates and shells reinforced by agglomerated carbon nanotubes.Tounsi and coauthors[22-25]investigated the buckling and vibration behaviors of FGM and FG-CNT mono and sandwich plates made of new generation materials on the elastic foundations using different boundary conditions and theories.Shen and Xiang [26-29]investigated nonlinear vibration and postbuckling of nanotube-reinforced composite cylindrical panels under axial and external pressures resting on elastic foundations in thermal environments.Mohammadi et al.[30]studied higherorder thermo-elastic analysis of FG-CNTRC cylindrical vessels surrounded by a Pasternak foundation.Duc et al.[31]presented thermal and mechanical stability of functionally graded carbon nanotubes (FG CNT)-reinforced composite truncated conical shells surrounded by the elastic foundations.

It is known that the influences of shear strains are very important for the buckling behavior of composite shells in different environments.The use of shear deformation shell theories(SDSTs)in the calculation of the critical parameters of composite shells allows one to overcome the disadvantages of the critical parameters when using CST [31-35].In recent years, various methods have been developed for studying the problems of stability and vibration of heterogeneous composite shells in different environments based on the SDSTs.Bousahla et al.[36]studied buckling and dynamic behavior of the simply supported CNT-RC beams using an integralfirst shear deformation theory.Babaei et al.[37]reported thermal buckling and post-buckling analysis of geometrically imperfect FGM clamped tubes on nonlinear elastic foundation.Sobhy and Zenkour [38,39]studied vibration and hygrothermal analysis of functionally graded graphene platelet-reinforced composite doubly-curved shallow shells and microplates on elastic foundations.

As can be seen from the literature review, no scientific studies have been carried out regarding the problem of loss of stability of CCSs reinforced with CNTs under combined loads, taking into account the influence of T-P-EF in the framework of the FSDST.The main purpose of this study is to examine the solution of this problem in detail.The study consists of the following sections:the first section is an introduction that evaluates the literature studies relevant to this study and presents the original features of the article.In sections 2 and 3,taking into account the T-P-EF effect,the problem is formulated and the basic equations are derived.In section 4, the basic differential equations are solved for specific boundary conditions, and a new and original expression for the combined buckling loads is obtained.After proving the correctness of the formulas obtained by comparison in Section 5, an original numerical analysis was carried out in the presence of elastic foundations and,finally, the comments are discussed in Section 6.

2.Formulation of the problem

2.1.Geometry and material properties

Consider composite conical shell reinforced by CNTs and resting on the two-parameter elastic foundation under a combined loading(Fig.1).The symbols characterizing the CCS are presented below:The thickness is,the large and small radii areand,the length of the truncated cone is,the semi-vertex angle is γ,the distance from the top of the cone to the small and large bases areand.The origin of the coordinate system is at the top of the cone and located on the middle surface,theaxis is directed along the generator,the θ axis is in the circumferential direction, and theaxis is perpendicular to the plane of these two axes and directed inward.The displacement components of any point on the reference surface in the，anddirections are shown asand, respectively.The two-parameter elastic foundation is used as the elastic foundation model and its mathematical expression is as follows [18]:

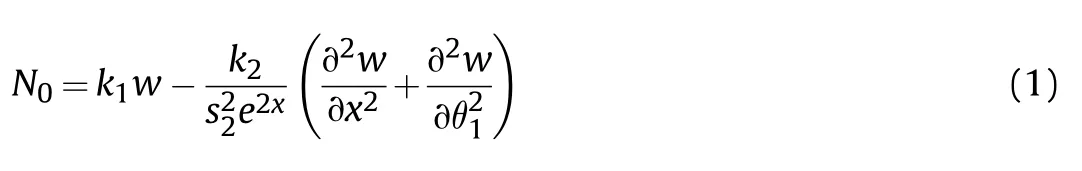
where θ= θ sinγ,= ln（/）,denotes the stiffness of the spring layer(in Pa/m),denotes the shearing layer stiffness of the foundation (Pa?m),is the reaction force of the T-P-EF per unit area on the shell reinforced by CNTs,and a coma is indicated partial differentiation versus the coordinates.

The composite conical shells reinforced by CNTs are subjected to a combined axial load and uniform hydrostatic pressure,as follows[14]:

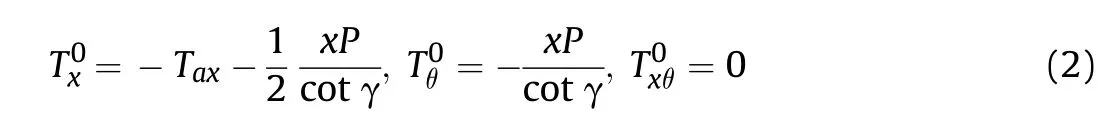
For convenience and simplicity, the extended mixing rule is used to express the effective material properties of CCSs reinforced by CNTs as follows [11,23]:

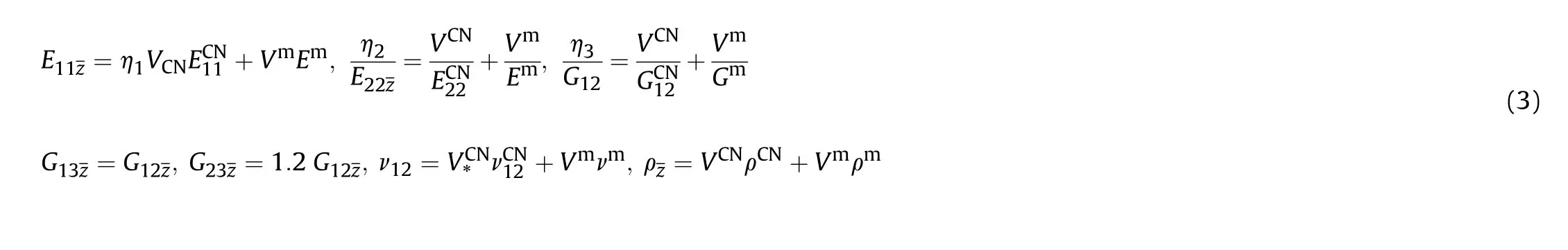
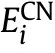
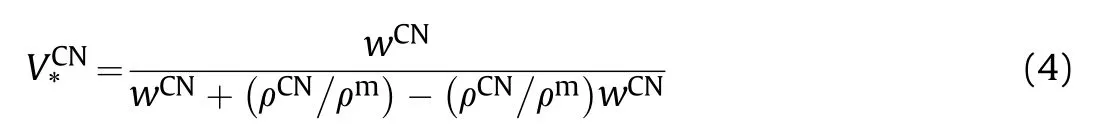
wheredenotes the mass fraction of nanotubes.

3.Governing relations and equations

The constitutive equations of CCSs reinforced by CNTs with linear distributions in the framework of the FSDST are built as[14]:

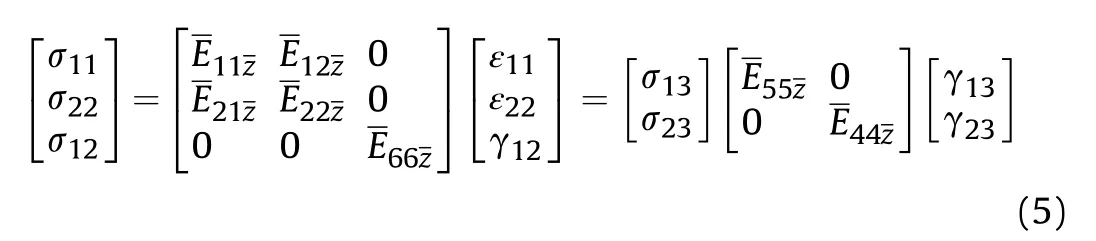
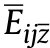
In the framework of the generalized first order shear deformation shell theory [14,32]in association with the modified Donnell shell theory, the governing equations for the CCSs reinforced by CNTs with linear distribution under combined loading and resting on the T-P-EF can be derived and expressed by

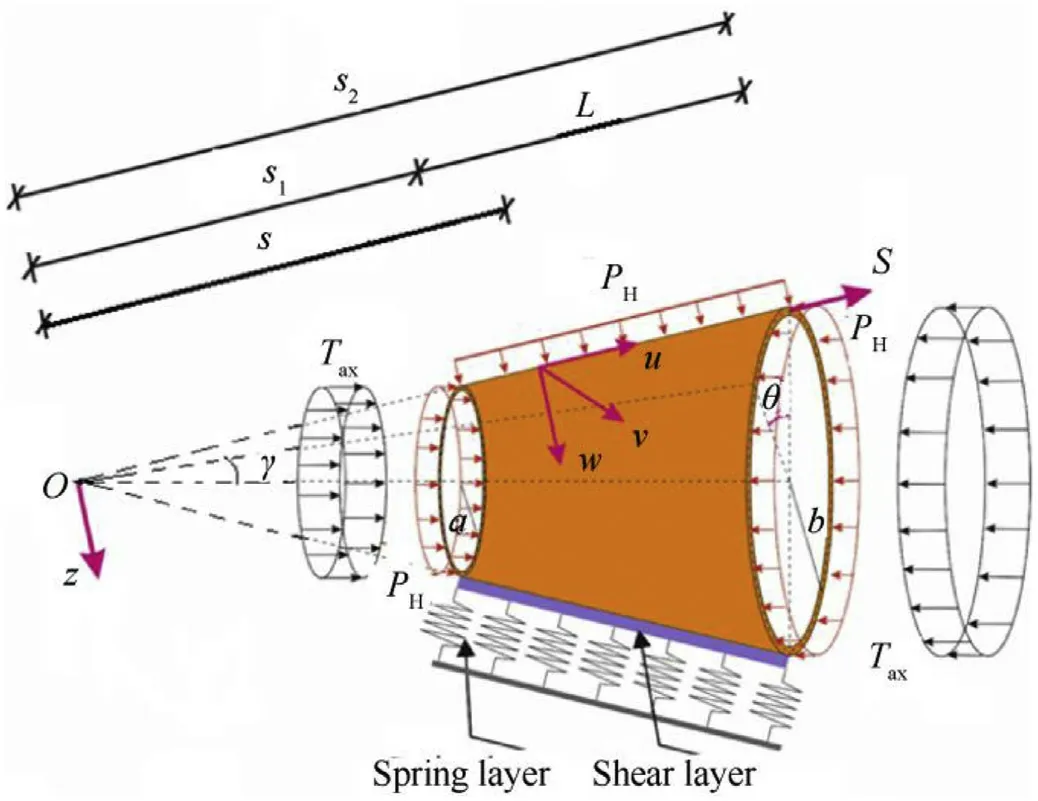
Fig.1.Composite shell reinforced by CNTs resting on the two-parameter elastic foundation and notations.

where Ψand Ψare the rotations of the normal to the mid-surface with respect to the θ- and s-axes, and Φ is the stress function defined by Refs.[32,40,41].

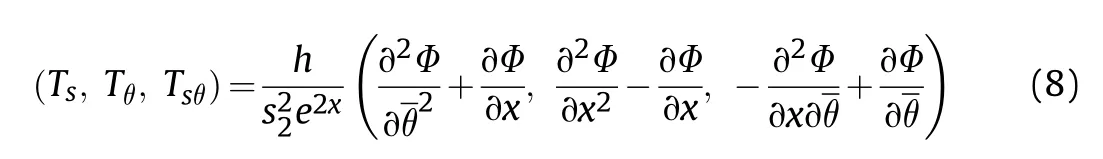
In the set of Eq.(7),L（，=1，2，…，4）are differential operators and are defined in Appendix A.

The set of Eq.(7)is the governing equations of carbon nanotubebased heterogeneous CCSs under combined loads and resting on the two-parameter elastic foundation within the FSDST.

4.Solution of governing equations

In this section we present the procedure to solve the eigen value problem, which includes the solution of partially differential equation for freely-supported boundary conditions.The approximation function is sought as follows [14]:

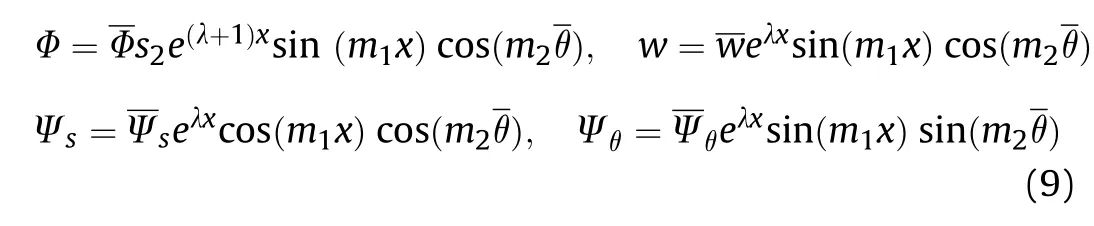
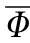
Introducing (9) into the system of Eq.(8), then applying the Galerkin procedure to the obtained equations, and using integration and some manipulations,we obtain algebraic equations,which for their non-trivial solution, the determinant of the matrix, consisting of the coefficients of the unknown, equals to zero:

where q（，=1，2，…，4）are the coefficients depending on the CCSs reinforced by CNTs,=-T--q-qin whichanddenote coefficients axial compression and hydrostatic pressure,respectively,qand qdenote coefficients of the T-P-EF,and are defined in Appendix B.

In order to find the expression for the combined load, we first find the analytical expressions for the axial buckling load and hydrostatic buckling pressure from the extended form of the determinant of Eq.(10).

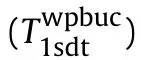
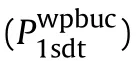
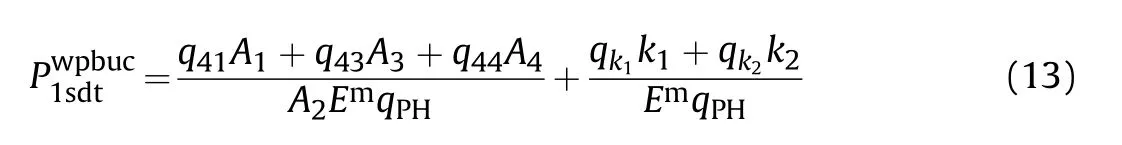
The critical combined axial load/hydrostatic pressure for CCSs reinforced by CNTs with linear distributions resting on the T-P-EF based on the FSDST,are obtained from the following relation[40]:

where=/and.=/

Under the assumptions= μ, in Eq.(14), we get the following expressions for combined (axial/hydrostatic) buckling load:

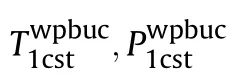
5.Results and discussion

5.1.Parameters used in numerical calculations

The numerical analyzes are carried out by changing eight parameters: volume fraction of SWCNT, CNT distribution, effective material properties methyl methacrylate (PMMA) and (10,10)armchair single walled CNTs(SWCNTs),foundation stiffness,shear strains shape functions, semi-vertex angle, γ,/and/ratios(see, Table 1).The values of the combined load for conical shells reinforced by CNTs are determined for different magnitudes ofλ,within a coupled stress theory context, in order to check for the effect of the FSDST on the critical loading condition.After a systematic numerical computation, it is found that for freelysupported CCSs reinforced by CNTs with linear distributions and resting on the T-P-EF,the critical combined hydrostatic/axial load is reached for λ = 2.4.The shear strain functions vary parabolically trough the thickness of the cones and given in Table 1, also.

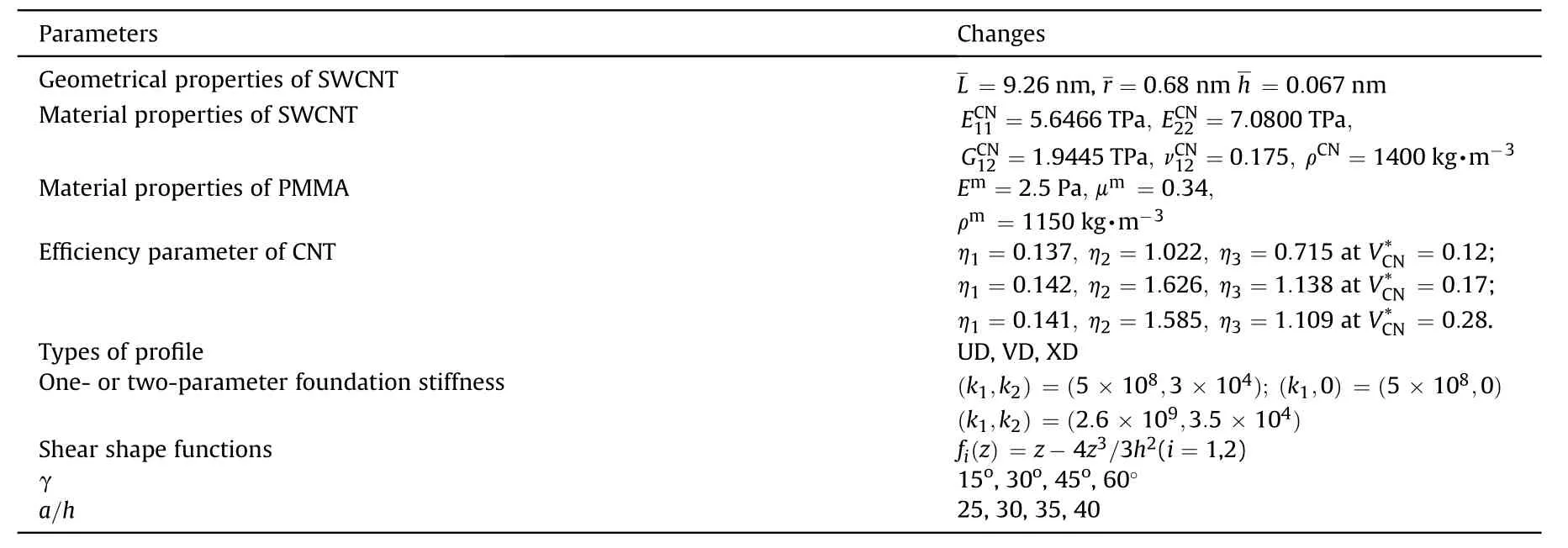
Table 1The parameters used in numerical analysis and their changes.

The concept of functionally graded carbon nanotube-reinforced composites(FG-CNTRCs)was defined by Shen[42]to better utilize a low percentage of CNTs in CNTRCs.It is believed that the volume fraction of CNTs varies linearly in the direction of thickness, and such an arrangement of CNTs is easily realized in practice.The distribution of the volume fraction of carbon nanotubes in the thickness direction of the matrix is mathematically expressed by the uniform distribution(UD)and two types of linear function(see,Fig.2) [11,22]:

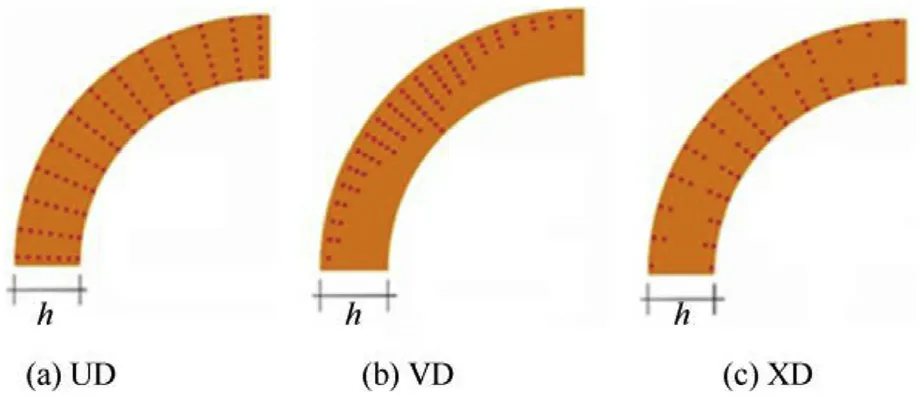
Fig.2.Different distribution patterns of CNTs in the matrix:(a)UD,(b)VD and(c)XD.

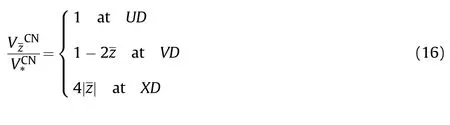
5.2.Comparison

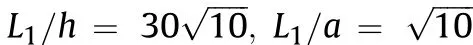
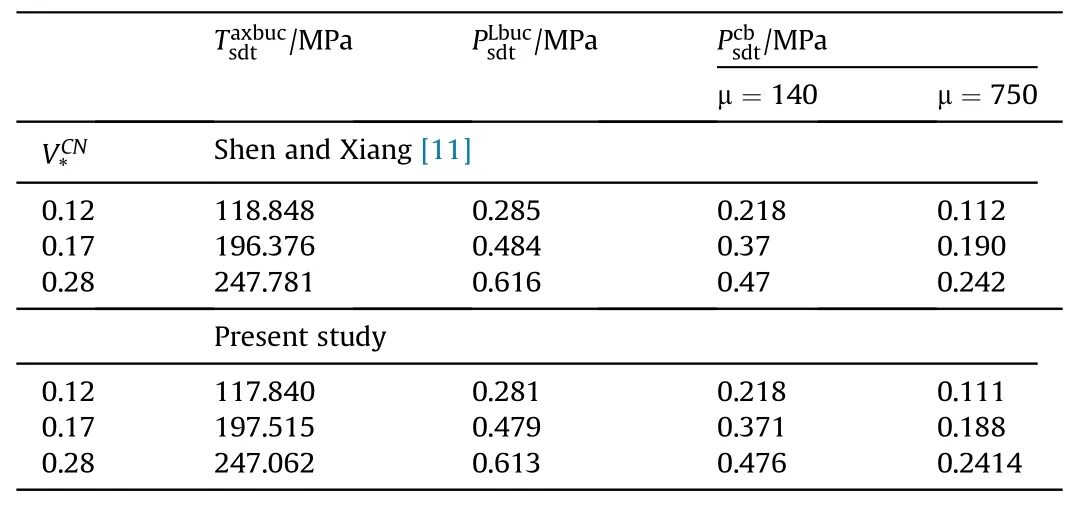
Table 2Comparative response of buckling loads for shear deformable cylinders reinforced by CNTs with X-type linear distribution.

Table 3Variation the CBL for CCSs reinforced by CNTs resting on the T-P-EF within the various shell theories versus the μ for various *and types of CNT distribution.

5.3.Specific analysis for CBLs

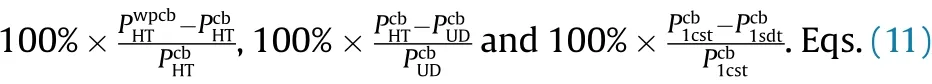
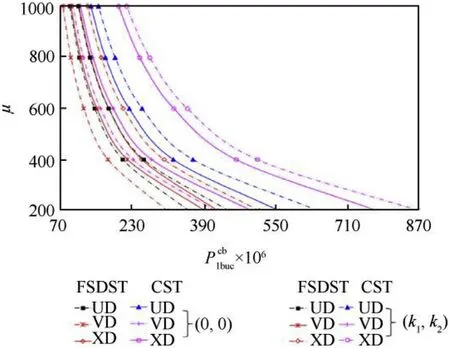
Fig.3.Variation the values of the CBL for CCSs reinforced by CNTs on the T-P-EF within the various shell theories versus the μ for = 0.12 and various types of CNT distribution.

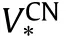
The influence of VD and XD-distributions on the CBL is weakened, in the presence of T-P-EF.In addition, the use of shear deformation theory significantly reduces the heterogeneity effect on the combined buckling load compared to the classical theory(see,Fig.3).It is observed that the influence of the T-P-EF on the CBL decreased due to the increase of the μ.It has been determined that the influence of the T-P-EF on the CBL within the framework of FSDST is more pronounced than the classical shell theory.In the presence of the T-P-EF, the influence of shear strains on the CBL decreases with the increase of μ, although it is slow, the highest effect is observed in the CCSs reinforced by CNTs with XD-distribution.

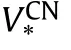
Fig.4.Variation of CBLs for CCSs reinforced by CNTs with UD- and XD-types distribution with and without EFs versus a/h for = 0.28.

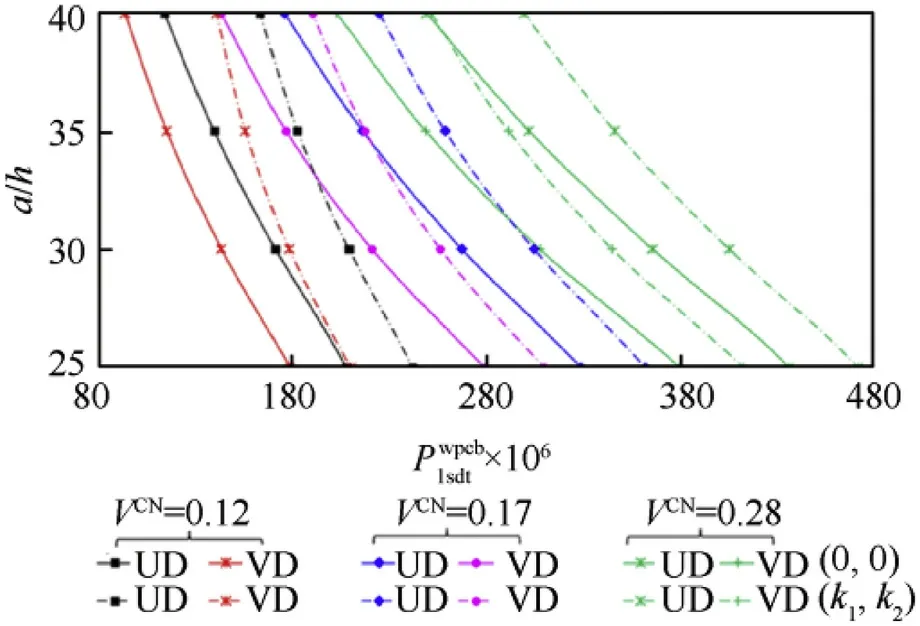
Fig.5.Variation of for CCSs reinforced by CNTs with UD and VD-types distribution with and without T-P-EF versus R1/h for a different

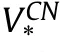
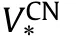
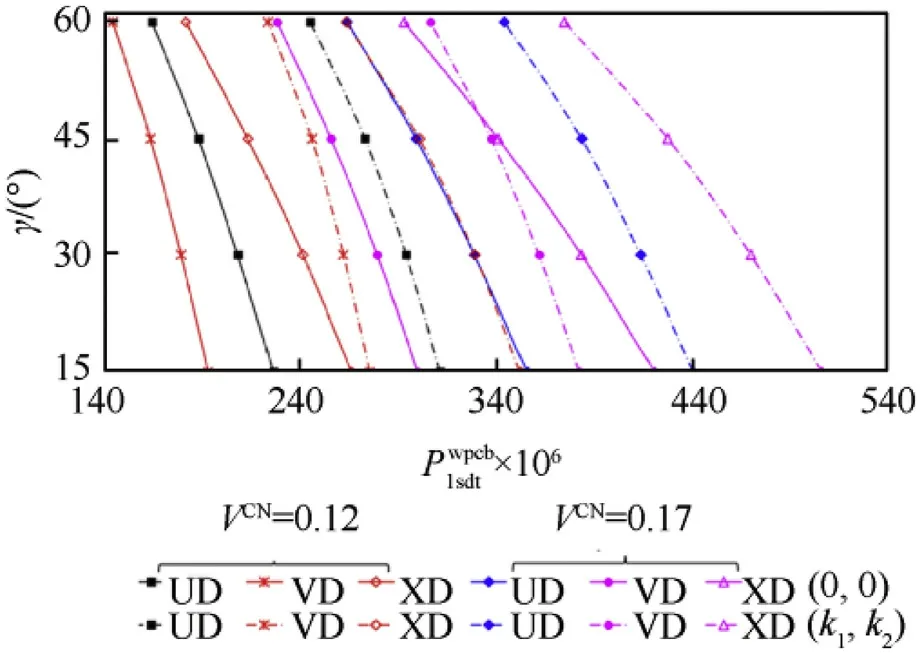
Fig.6.Variation of CBLs for UD,VD and XD-CCSs with and without T-P-EF within two different shell theories versus the semi-vertex angle, γ, for the different .

Fig.7.Variation of CBLs for UD and VD-CCSs with and without T-P-EF in the framework of two different shell theories versus the semi-vertex angle, γ, for the different.

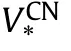
6.Conclusions

In this study the buckling analysis of CCSs reinforced with CNTs subjected to combined loading of hydrostatic pressure and axial compression resting on the T-P-EF.The governing equations of CCSs reinforced by CNTs are derived in the framework of the FSDST that includes shell-foundation interaction.The governing equations are solved by using the Galerkin procedure to determine the combined buckling loads of the structure selected here.The stability equations are solved by using the Galerkin procedure to determine the CBLs of the structure selected here.

Numerical analysis led to the following generalized results:

a) The number of waves corresponding to the values of the CBL reduces with the increase of load-proportional parameter,and this reduce becomes more evident in the presence of the T-P-EF.

b) The influence of VD and XD-distribution shapes on the CBL is weakened,in the presence of T-P-EF,further the use of FSDST significantly reduces the heterogeneity effect on the combined buckling load compared to the CST.

c) Although the magnitudes of the CBL for CNT-based CCSs increase, its values decrease with increasing of the loadproportional parameter in the presence of T-P-EF.

d) In the presence of the T-P-EF,the influence of shear strains on the CBL for CCSs decreases with the increasing of the loadproportional parameter, although it is slow, the highest effect is observed in the CCSs reinforced by CNTs with XD-distribution shape.

e) The influence of heterogeneity and shear strains on the CBL for CCSs reinforced by CNTs is less pronounced on the T-P-EF compared to the one-parameter EF or W-EF.

f) The influences of one-or two-parameter EFs on the CBLs for CCSs reinforced by CNTs are more pronounced in the framework of FSDST compared to the CST.

g) The values of the CBL of composite conical shells reinforced by CNTs with and without T-P-EF decrease for the increasing of the semi-vertex angle.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The differential operators L（，=1，2，…，4） are defined as