基于混合變分自編碼器回歸模型的軟測量建模方法

崔琳琳 沈冰冰 葛志強

在實際工業生產過程中,需要對一些關鍵的質量變量進行實時測量,如產品濃度、過程氣體含量、催化劑活性和熔體指數等,這對實現有效的過程控制和提高產品質量具有重要意義[1-5].然而,由于極端的測量環境、昂貴的儀器成本、大的分析測量延遲等因素,關鍵質量變量的物理測量難以實現[6-8].因此,軟測量技術應運而生.軟測量是一種虛擬傳感器技術,通過構建數學模型,以一組容易測量的相關過程變量為輸入,以過程關鍵質量變量為輸出,來快速準確地估計這些難以直接測量的質量變量[9-11].一般來說,軟測量方法可大致分為兩種,模型驅動的軟測量和數據驅動的軟測量[12-13].與前者相比,數據驅動的軟測量方法不需要精準的機理模型和大量的過程專家知識,更加具有靈活性和實用性.此外,隨著分布式控制系統(Distributed control systems,DCSs)在現代工業過程中的廣泛使用,收集到的數據也日益增多,為數據驅動建模方法提供了豐富的數據保證[14].因此,數據驅動的軟測量方法受到了越來越多的關注.經典的基于數據驅動的軟測量建模方法有主成分回歸分析(Principal component regression,PCR)[15]、偏最小二乘法(Partial least squares,PLS)[16]、支持向量機(Support vector machine,SVM)[17]和人工神經網絡(Artificial neuralnetwork techniques,ANN)[18]等.

近年來,深度學習作為一種新興技術,在圖像處理、計算機視覺、自然語言處理等應用領域都取得了很大的進展.與傳統的淺層方法相比,深度學習方法具有更深的網絡結構,它能夠通過多層非線性映射,從數據中提取更深層的抽象特征,具有強大的數據建模能力.因此,面對越來越復雜的大規模現代工業過程,深度學習具有不可替代的優勢,已經被應用到了軟測量領域當中[19].例如,Yao和Ge 提出了一種基于分層極限學習機的半監督深度學習軟測量模型[20].Yuan 等開發出一種質量相關自動編碼器,用于提取深層次的輸出相關特征[21].Zhang和Ge 基于門控循環單元和編碼解碼網絡,設計了一種深度可遷移動態特征提取器,并應用于軟測量[22].Zheng 等將集成策略、深度信念網絡和核學習集成到軟測量框架中,建立了集成深度核回歸模型,并擴展到半監督形式[23].然而,由于過程的隨機擾動等原因,幾乎所有的過程數據都會受到隨機噪聲的污染,從本質上來說,過程變量都屬于隨機變量[14,24-25].最近,Kingma和Welling 提出了變分自編碼器[26],一種深度生成模型,它結合了深度學習和貝葉斯變分推斷.作為一種以深層神經網絡為結構的概率框架模型,VAE 既具有深度學習的非線性特征提取能力,又能像概率模型那樣對過程不確定性和數據噪聲進行建模.基于這些優點,VAE已經被引入到工業過程中,并逐漸被用于過程監測和軟測量建模等應用場景[27-31].

盡管目前VAE 在軟測量應用中取得了一些進展,但是傳統的VAE 通常假設其潛在變量分布服從高斯分布,因此模型學習到的特征表示只能是單峰形式,難以充分發揮潛在空間編碼的能力和靈活性.這在很大程度上限制了VAE 對復雜特性過程數據的描述,如工業領域廣泛存在的多模態數據,VAE 的建模性能很難得到有效的保障.在實際工業過程中,由于原料比例、產品需求、制造策略等因素的變化,經常會發生操作條件的轉變,即工況發生變化,從而使過程數據呈現典型的多模態特性[32-34].近年來,學者們提出了一些VAE 變體模型,通過使用復雜的先驗等手段來促進編碼的靈活性,但他們的目標大多是進行無監督聚類[35-37].到目前為止,還沒有VAE 在多模態工業過程軟測量應用中的相關研究報導.基于以上討論,本文結合高斯混合模型的思想,基于VAE 框架提出一種混合變分自編碼器回歸(MVAER)模型,用于解決多模態過程的質量預測問題.該方法采用高斯混合模型來描述VAE 的潛在空間變量分布,分別對應工業過程中的多個模態.通過非線性映射將復雜多模態數據映射到潛在空間,學習各模態下的潛在變量,獲取原始數據的有效特征表示.同時,建立潛在特征表示與關鍵質量變量之間的回歸模型,實現軟測量應用.通過一個數值算例和一個實際工業案例,驗證了所提方法的有效性和可行性.

本文的其余部分組織如下.在第1 節中,簡要回顧了VAE 模型.在第2 節中,介紹了所提出的MVAER 模型的主要思想和詳細的推導過程,并介紹了基于MVAER 的軟測量建模與應用方法.在第3 節中,通過兩個案例對MVAER 進行了性能評估.最后,在第4 節中得出本論文的結論.

1 VAE 概述

VAE 是一種無監督的深度生成模型,結合了深度學習和貝葉斯概率推斷的觀點.它假設數據x是由某個具有不可觀測的連續隨機隱變量z的隨機過程產生的.觀測數據的邊際似然可以寫為:

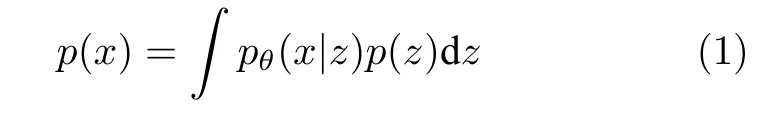
其中,pθ(x|z) 是生成模型,可以被描述為多元高斯分布,p(z) 是先驗,通常被簡單地設置為標準高斯分布 N (0,1) .

根據貝葉斯定理,可以得到隱變量z的后驗分布為.然而,由于生成模型的參數θ和隱變量都是未知的,這里隱變量的積分和后驗概率都是難以處理的.因此,VAE 根據變分推斷的思想,引入一個額外的變分分布qφ(z|x) 作為推斷模型,來近似難解的真實后驗.與生成模型相似,推斷模型qφ(z|x) 也可以描述為多元高斯分布.

VAE 的優化目標是最大化邊際似然函數的證據下界.

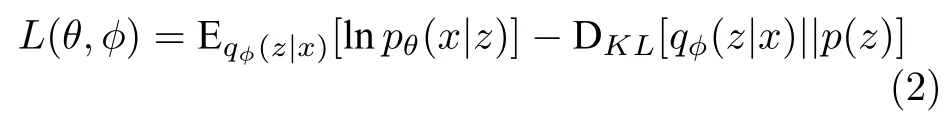
其中,等號右邊的第一項是給定pθ(x|z) 時,lnpθ(x|z)的期望,用來保證重建數據與真實數據之間的匹配程度;第二項是一個Kullback-Leibler (KL)散度項,可以被看作是一種正則化,指導近似后驗分布盡可能地接近先驗分布.

VAE 的模型結構如圖1 所示.可以看到,在VAE 中,推斷模型qφ(z|x) 被參數化為一個參數為φ的神經網絡,稱為概率編碼器.它將輸入數據映射到低維潛在空間,得到其隱變量表示z,這可以看作是對輸入數據的特征提取;pθ(x|z) 被參數化為另一個參數為θ的神經網絡,稱為概率解碼器,它從潛在空間中重建原始數據.通過最小化負變分證據下界,同時優化模型的參數φ和θ.更多詳細內容可以參考文獻[26,38-39].

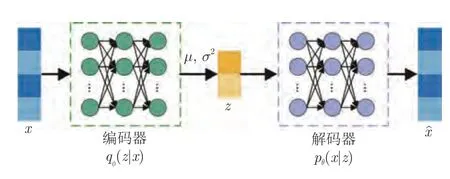
圖1 VAE 模型結構圖Fig.1 Model structure of VAE

2 基于混合變分自編碼器回歸模型的軟測量方法

在實際應用中,傳統的基于VAE 的軟測量方法難以對工業中廣泛存在的多模態數據進行有效的特征提取.為了解決這一問題,本節將提出一種混合變分自編碼器回歸模型,并將其應用于軟測量模型的構建.總體而言,該方法結合了VAE 框架和高斯混合模型,并將特征提取和回歸建模融為一體,使其對復雜多模態過程的關鍵質量指標數據具有更好的預測性能.

2.1 混合變分自編碼器回歸模型

混合變分自編碼器回歸模型本質上是建立在VAE 框架上,同樣可以通過生成模型和推斷模型來描述.

模型假設輸入數據x由隨機連續潛在變量z生成,z在潛在空間中服從高斯混合分布.為了建立關鍵質量變量,即輸出變量y的回歸模型,假設y也由潛在變量z生成,那么生成過程可以描述為:

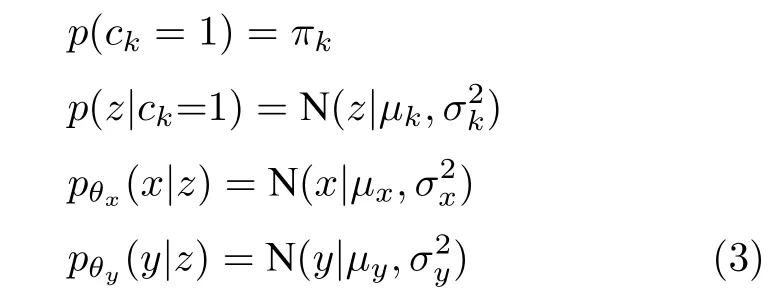
根據上述生成過程,生成模型可以用聯合概率分布表示并被分解為:

數據樣本點的邊緣概率p(x,y) 的 l og 似然函數可以推導為:

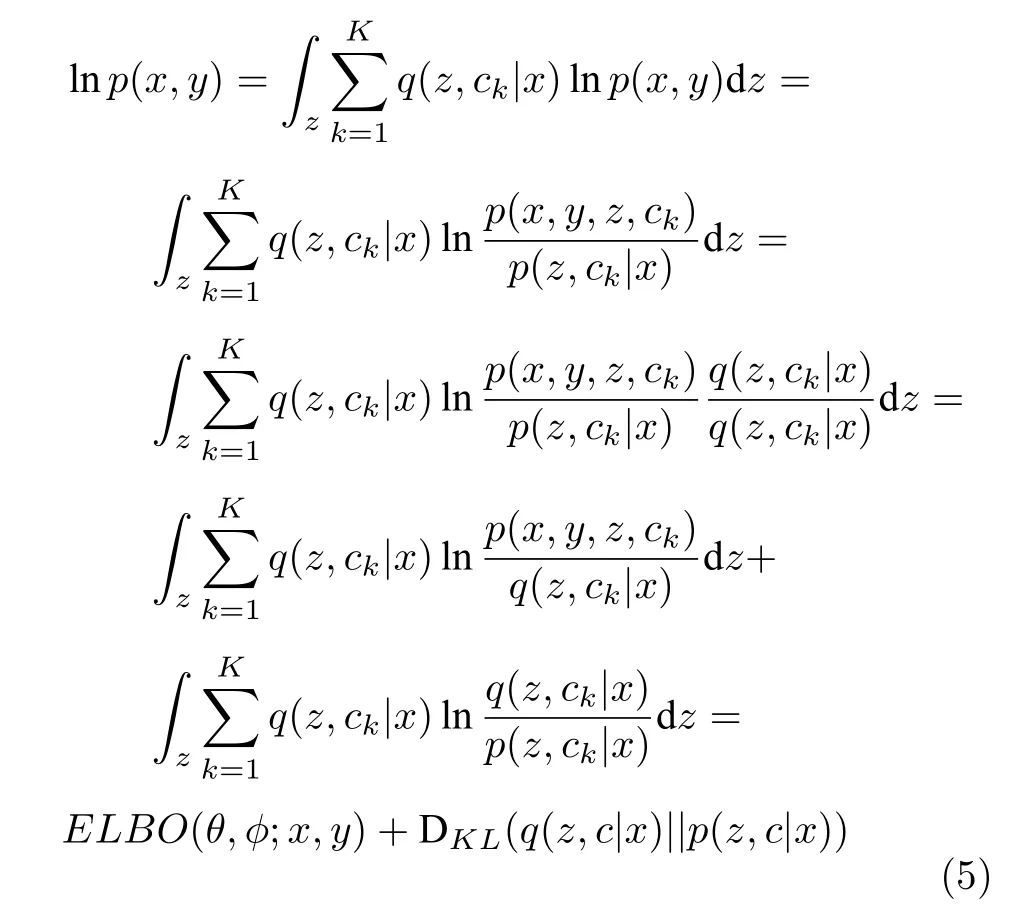
其中,ELBO(θ,φ;x,y) 是邊緣概率似然函數的證據下界;qφ(z,c|x) 是推斷模型,作為一個額外引入的變分后驗,用來逼近難以計算的真實復雜后驗p(z,c|x),可以被分解為:

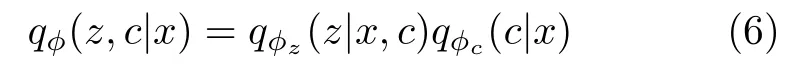
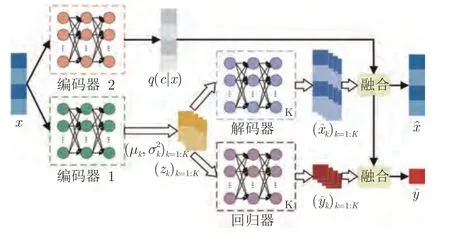
圖2 混合變分自編碼器回歸模型結構圖Fig.2 Model structure of the MVAER model

結合式(4)～ (6),模型的ELBO 可以重寫為:

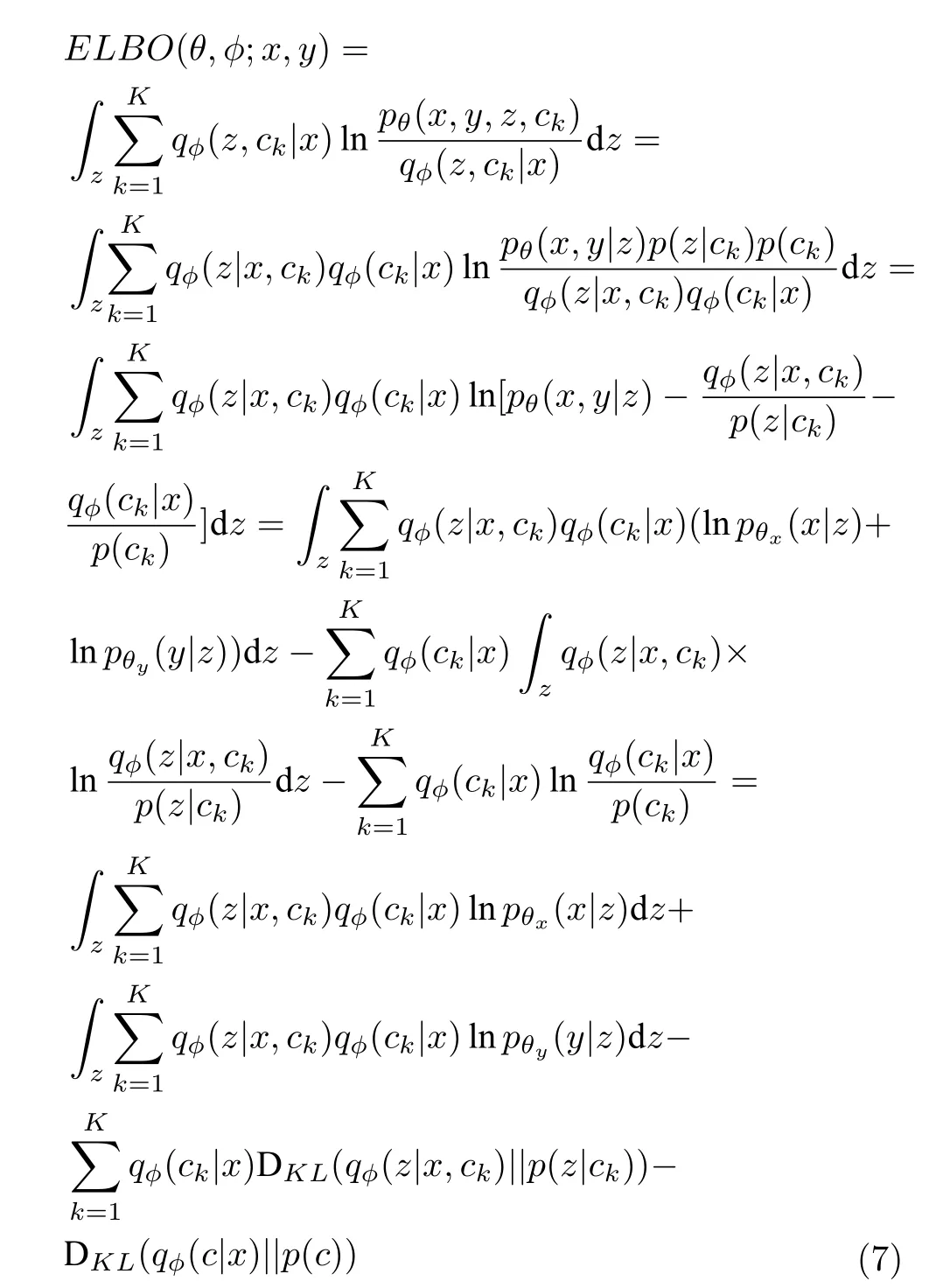
與VAE 相似,為了計算參數φ和θ,需要最大化上述的證據下界ELBO(θ,φ;x,y),這相當于最大化邊緣概率似然函數.

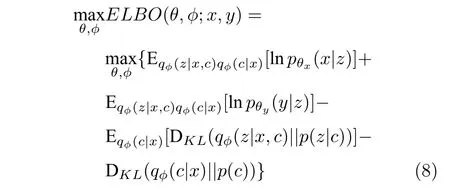
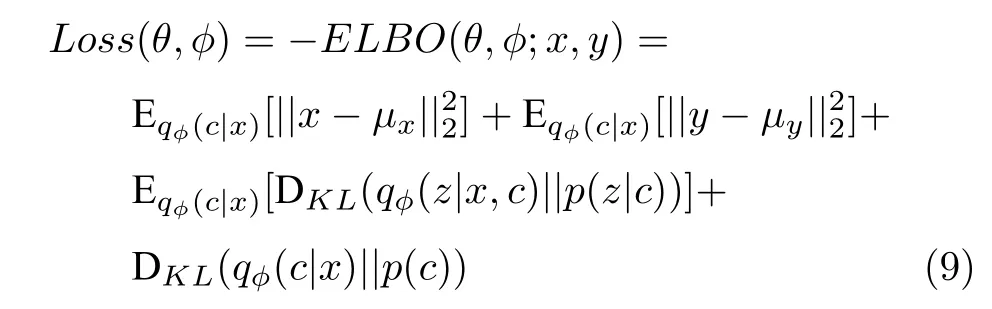
其中,μx通過模型解碼器得到,μy通過模型回歸器得到;表示數據在每個模式下的潛在特征所服從的高斯分布,其均值和方差通過模型編碼器得到;qφ(c|x) 表示數據屬于每個模式的可能性,通過帶有Softmax 層的編碼器計算得到.基于最小化損失函數的優化目標,可以通過隨機梯度下降等優化算法,對模型參數φ和θ進行更新優化.

損失函數中的前兩項是輸入數據的重構誤差和輸出數據的預測誤差項,能夠鼓勵模型很好地重構輸入數據和預測輸出數據;后兩項是有關連續潛變量z和離散潛變量c的KL 散度項,有助于將原始數據中的變化傳播到潛在空間中的隱變量中去,并使后驗和先驗之間更好地匹配.模型期望潛在空間中的離散隱變量c能夠表示與原始混合分布中相對應的數據集群;潛在空間中的連續隱變量z能夠表示每個集群內的數據變化.

2.2 基于MVAER 模型的在線軟測量方法

在上一小節中,詳細推導了MVAER 模型.當該模型用于工業過程在線軟測量時,就是對當前樣本,表示為xnew,提供相應的質量變量預測.

假設模型中p(y|z)=N(μy,k,I),其中z～q(z|xnew,ck),k=1,2,···,K,那么當前數據樣本的質量變量預測值計算為:

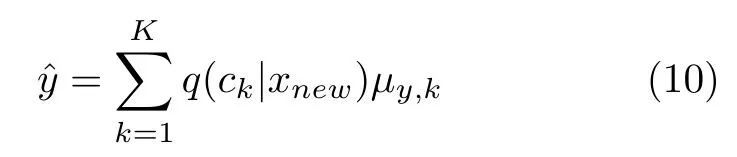
其中,q(ck|x) 表示當前數據樣本屬于第k個混合成分的可能性,可以通過模型中的編碼器得到,計算公式如式(11)所示,公式中表示該編碼器除最后Softmax 層之外的部分所代表的函數,則代表該部分的網絡參數;μy,k表示當前樣本質量變量y服從的高斯分布的均值,將其視為y的預測值,可以使用樣本的潛在特征zk為輸入,通過模型中的回歸器得到,計算公式如式(12) 所示,公式中f(·;θy) 表示回歸器所代表的函數,θy則代表回歸器的參數.取所有混合成分下的預測值的加權和作為質量變量的最終預測值.

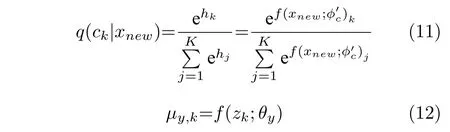
接下來,我們詳細介紹基于MVAER 模型的實際工業過程軟測量應用過程.該過程主要包括兩部分,離線建模和在線預測.

在離線建模階段,首先要根據理論分析和操作經驗選擇模型的輸入變量,并采集數據(包括輸入變量和質量變量).對收集到的數據進行標準化處理,然后訓練MVAER 模型.當模型訓練完成后,保存模型參數用于在線質量預測.在線預測時,對于新采集的待預測樣本,需要對其進行與離線建模時相同的數據預處理,然后將其送入訓練好的模型中,得到質量變量的預測結果.所提出的基于MVAER 模型的軟測量建模算法總結如算法1 所示,并將整個過程直觀地體現在如圖3 所示的流程圖中.

圖3 基于MVAER 的軟測量建模流程圖Fig.3 Flowchart for soft sensor modeling based on the MVAER model

為了直觀地評價模型的性能,本文使用均方根誤差(Root mean squared error,RMSE)和R2系數兩個指標來量化模型的預測效果.RMSE和R2定義如下:

其中,N是樣本個數,yi是第i個樣本的實際輸出值,是第i個樣本的預測輸出值,是所有樣本實際輸出值的平均值.RMSE 代表預測誤差,R2表示實際值和預測值之間的平方相關關系.通常,RMSE越小,R2越接近于1,模型的預測性能越好.

3 案例分析

3.1 數值例子

本節設置了一個具有三種運行模式的數值算例,各個高斯組分和關系的具體情況如表1 所示.每個模式下輸入和輸出之間的關系都是非線性的.為了構建模型,生成500 個樣本作為訓練集用于模型訓練,生成500 個樣本作為測試集用于模型性能測試.圖4 中分別顯示了X和Y的數據分布,可以直觀地看出該算例具有多模態行為.

表1 數值算例的配置Table 1 Configuration of the numerical example

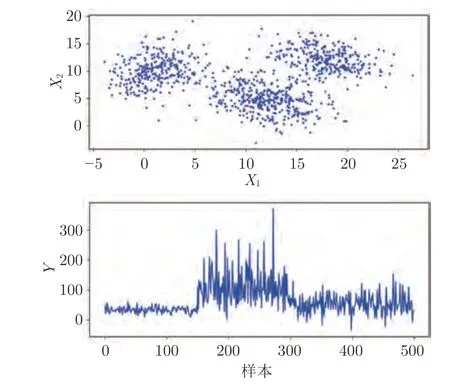
圖4 數值算例的數據模式Fig.4 Data pattern of the numerical example

為了驗證MVAER 算法的有效性,將其與偏最小二乘(Partial least squares,PLS)、高斯混合回歸(Gaussian mixture regression,GMR)、自編碼器(Auto-encoder,AE)、變分自編碼器(Variational auto-encoder,VAE)方法進行比較.其中,PLS是一種傳統回歸模型,GMR 是一種典型的多模式建模方法,AE 是常用的深度學習建模方法,VAE則是所提出的MVAER 模型的基礎框架.

在MVAER 算法中,將編碼器和譯碼器設置為具有單層隱藏層,隱藏層的神經單元個數為6;潛在變量的維度設為2;為了方便,回歸網絡設為一個全連接層,即在提取的特征和輸出之間建立一個線性關系;組分個數設為3,這是已知的.GMR 的組分個數設為3.每個模型在測試集上的數值評價指標在表2 中列出.

表2 PLS、GMR、AE、VAE和MVAER模型的性能評價指標Table 2 Performance evaluation indices of PLS,GMR,AE,VAE and MVAER models

從中可以發現,MVAER 模型的性能明顯優于其他模型.PLS、GMR、AE、VAE和MVAER 的詳細預測值如圖5 所示,散點圖如圖6 所示.

圖5 PLS、GMR、AE、VAE和MVAER模型的預測結果圖Fig.5 Predicted results of PLS,GMR,AE,VAE and MVAER models

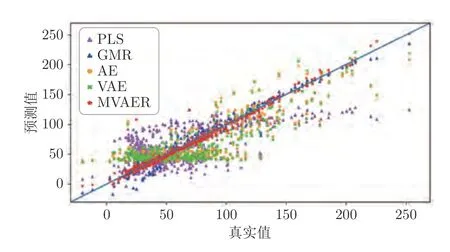
圖6 預測結果散點圖Fig.6 The predicted scatter points of different models

從預測曲線中可以直觀地看出,PLS 在每個模態下都不能很好對輸出值進行預測.相比之下,AE和VAE 模型對于該過程的回歸預測效果有所改善,對第二模態樣本有較好的預測效果.然而,AE和VAE 模型對第一模態和第三模態樣本具有較差的預測能力,從圖中可以看出在這兩個模態下它們的預測結果趨于直線,這表明模型沒有學習到相關的數據特性和耦合關系.GMR和MVAER 對所有模式下的數據樣本都有良好的擬合能力,但與GMR相比,MVAER 的預測曲線更加貼合真實曲線,具有更高的預測精度.從散點圖中,也能得到相似的結論.散點圖結果表明,PLS 等模型的預測結果分布較為分散,存在較大的預測偏差,而MVAER 模型的預測結果更加集中和靠近主對角線,這意味著它的預測效果最好.以上比較和分析表明,PLS 作為線性模型,不能有效提取數據中的非線性和多模態特性,因此不能很好地處理具有復雜特性的過程,而 AE和VAE 模型雖然可以處理非線性關系,但無法同時對多個模態下的耦合關系進行建模.GMR和MVAER 模型則可以較好地適應多模態過程,并且當輸入輸出之間非線性相關時,MVAER 的性能優于GMR.

3.2 工業例子

該工業案例取自于合成氨過程中的制氫裝置,氫氣是合成氨氣的重要原料之一.根據工藝設計,氫氣生產過程中的關鍵反應在一段轉化爐中進行,主要是通過脫碳反應將脫硫天然氣轉化為氫氣.過程的工藝流程圖如圖7[28]所示.根據反應機理,溫度對氫氣的含量和純度有很大的影響,而爐內溫度主要取決于稠密燃燒器的燃燒條件.燃燒條件則是通過調節爐內氧氣含量來控制的.因此,控制一段爐頂部氧氣濃度在規定的范圍內是十分重要的.在實際生產過程中,氧氣含量通常由昂貴的質譜儀測量得到.為了降低生產成本,有必要構建一種軟傳感器在線估計氧氣含量.

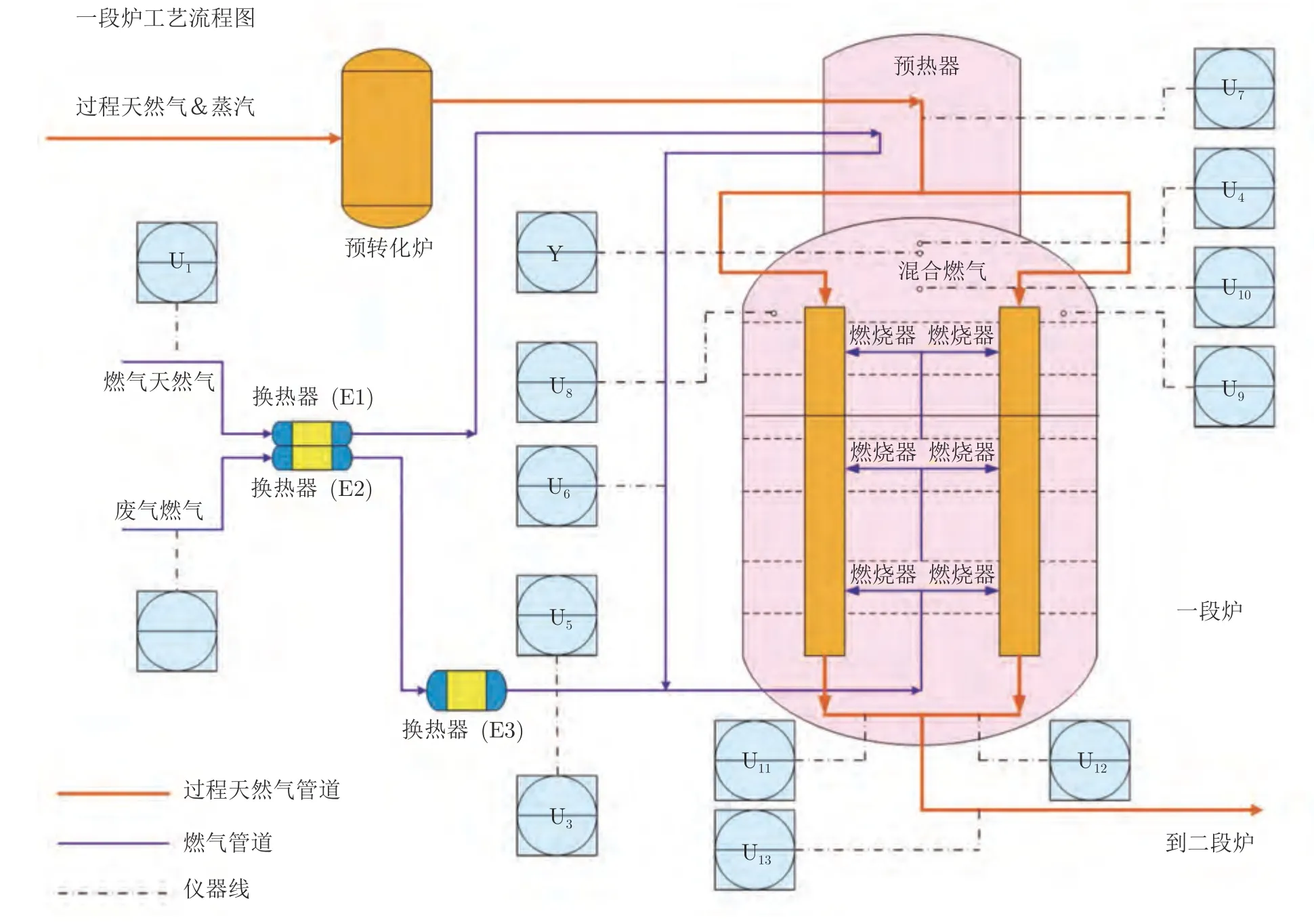
圖7 一段爐工藝流程圖Fig.7 Flowchart of the primary reformer

選擇13 個過程變量作為軟測量模型的輸入變量,包括溫度、流量和壓力,它們易于測量且和氧氣含量變化有關.這13 個過程變量的詳細說明列于表3.收集5 000 個樣本用于構建軟測量模型,其中2 500 個樣本作為訓練集,其余樣本作為測試集.為了展示MVAER 的有效性,構建PLS、GMR和VAE模型進行性能比較.通過試錯方法,將MVAER 的組分個數K設置為4,編碼器的隱藏層神經單元個數設置為32,隱變量的維度設為10,解碼器的結構與編碼器對稱,回歸器與上述數值算例中的一樣,是一層全連接層.GMR 的組分個數設置為9.VAE 模型的結構參數與MVAER 中對應的參數保持一致.

表3 一段爐過程變量描述Table 3 The description of the process instruments in the primary reformer

各種方法的性能評價指標,RMSE和R2,列于表4.通過比較這些結果可以發現,多模態建模方法優于非多模態方法,非線性方法優于線性方法.其中,MVAER 模型的預測性能最好.

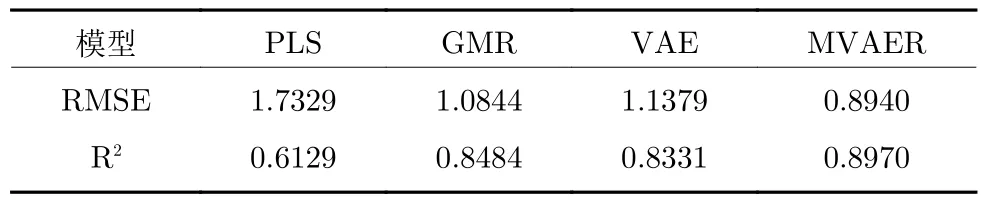
表4 PLS、GMR、VAE和MVAER模型的性能評價指標Table 4 Performance evaluation indices of PLS,GMR,VAE and MVAER models

PLS、GMR、VAE和MVAER 對氧氣濃度的預測結果如圖8 所示.直觀上,從圖中可以看出,PLS 模型的預測結果比較平穩,不能很好地追蹤氧氣濃度的變化.其余三種方法的預測效果都優于PLS 模型.其中,VAE 雖然大體上能捕捉氧氣濃度的變化趨勢,但其預測波動較大,預測曲線上有較多的毛刺;相比之下,GMR 模型能較好地對氧氣濃度進行預測,但是其預測曲線存在較多的尖峰現象.與VAE和GMR 相比,MVAER 模型的預測效果則有了明顯改善.MVAER 模型的預測曲線毛刺、尖峰現象更少,與真實值曲線吻合度較高,這意味著我們的模型有更強的擬合能力和更高的預測精度.幾種模型的預測誤差和預測散點圖分別如圖9和圖10 所示,從中也能得到相似的結論.具體來說,圖9 中顯示MVAER 模型的預測誤差小于其他幾種方法,大多處于-2和+2 之間.圖10 中顯示,MVAER 模型的預測結果分布更加集中,并且最為接近主對角線,這些結果都反映出MVAER 模型具有較好的預測性能.

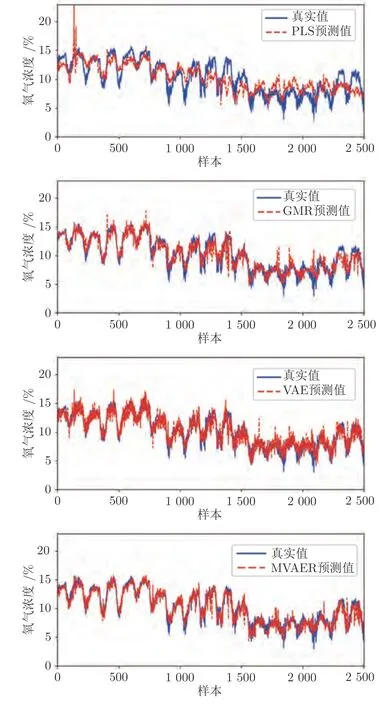
圖8 PLS、GMR、VAE和MVAER 模型的預測結果圖Fig.8 Predicted results of PLS,GMR,VAE and MVAER models

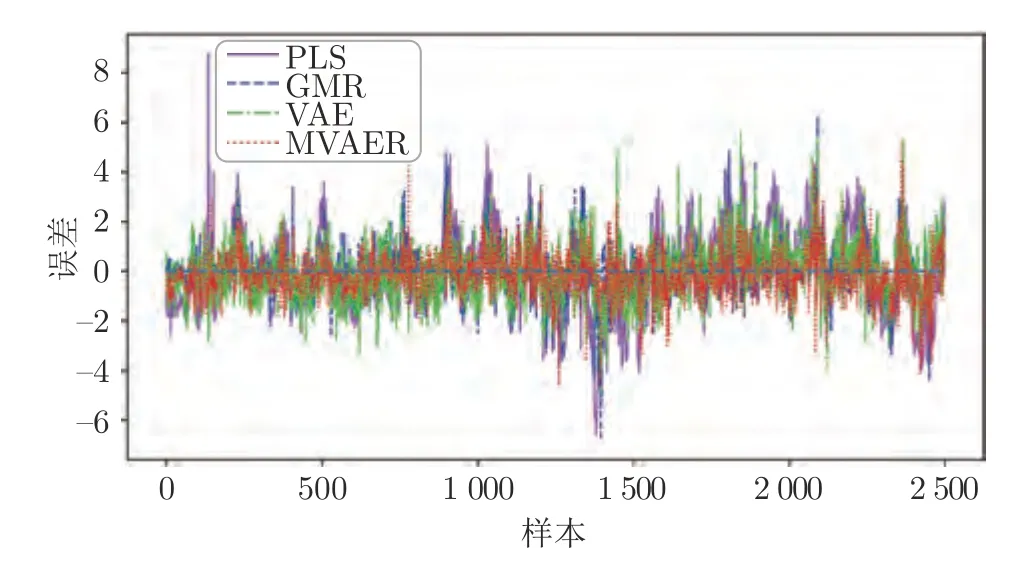
圖9 預測誤差圖Fig.9 The prediction errors of different models

圖10 預測結果散點圖Fig.10 The predicted scatter points of different models

總體而言,以上兩個實例的比較和分析表明,面對復雜多模態過程,本文所提出的MVAER 模型在捕獲數據多模態特性和非線性等方面表現出較強的能力,能夠有效地對關鍵質量變量進行預測.

4 結論

本文提出了一種新的混合變分自編碼器回歸模型,并將其用于復雜多模態工業過程的產品質量軟測量.通過結合高斯混合模型的思想,該方法打破了傳統VAE 中潛在空間單峰分布的限制,能夠有效地提取復雜多模態數據的潛在特征,并利用潛在特征對產品質量變量進行回歸建模.此外,該方法由于其混合概率框架,在不同模態下將會自動進行質量預測.在兩個案例中,包括一個數值例子和一個合成氨生產過程一段爐實際工業過程,與其他幾種方法相比,基于混合變分自編碼器回歸模型的軟傳感器預測性能最好,驗證了所提方法的有效性和可行性.最后,考慮到過程數據中有標簽數據稀少的實際情況,后續研究工作可以結合半監督學習,將所提方法擴展為半監督軟測量方法.