旋轉坐標系N-S方程無網格/網格混合算法

曹 騁 ，陳紅全 ，張加樂 ，高煜堃

（1.常熟理工學院機械工程學院，江蘇 常熟 215500；2.南京航空航天大學航空學院，南京 210016；3.安徽工業大學機械工程學院，安徽 馬鞍山 243002）

0 引言

槳葉是渦槳發動機最為重要的氣動部件之一，其旋轉流場也是計算流體力學（Computational fluid dy?namics，CFD）數值模擬的難點。槳葉氣動特性的優劣直接影響發動機性能。因此，發展能準確模擬旋轉槳葉氣動特性的CFD 算法，對渦槳發動機設計與研究具有重要的工程意義。

類似發動機槳葉這樣的旋轉體繞流在工程中廣泛存在，如旋翼飛行器等。傳統的CFD 技術在模擬這類流場時會遇到2 個難點。一個是目前的CFD 軟件大多基于“網格算法”，涉及計算域網格生成。但對于存在旋轉槳葉的渦槳發動機等多體復雜氣動外形，要生成合適的整體網格，刻畫出局部間隙等幾何細節，在網格拓撲約束下并非易事，常需要用到塊結構等特殊處理技術；另一個是因旋轉產生的動邊界問題的處理。目前的求解方法通常基于動網格技術開展，在處理動邊界大位移問題時，常需要結合網格重構、網格重疊等特殊處理技術，涉及到與角速度相關的旋轉特征物理量的插值運算，這會影響到算法的計算效率與精度。為了突破網格拓撲的制約，Batina等、蒲賽虎、郭曼麗等提出1 類無網格算法，計算域用無網格點離散，既可直接布點，也可用現有的結構或非結構網格點，涉及的空間導數等物理量僅依據當地點云結構逼近確定，其靈活性更適合處理旋轉體等復雜的幾何外形；為了準確反映旋轉角速度等特征物理量，Chen等發展了一種直接求解旋轉坐標系下控制方程的方法。旋轉運動網格在旋轉坐標系可與物體保持相對靜止，無須反復重構，旋轉特征物理量等也無須插值運算；像渦槳發動機的旋轉槳葉、懸停旋翼等非定常繞流，在旋轉坐標系下還可被看作準定常，減少了求解的復雜度。基于這些特點，該方法已在渦輪機械和旋翼繞流的模擬中獲得廣泛應用。但將無網格算法和旋轉坐標系下控制方程結合起來應用于求解槳葉這樣的旋轉體繞流問題，還鮮有文獻報道。

本文發展一種基于旋轉坐標系的無網格/網格混合算法，用于求解槳葉等旋轉物體的黏性繞流問題。基于無網格點云空間導數逼近等方法離散控制方程，并結合隱式LU-SGS 算法，發展形成求解非定常問題的雙時間步隱式格式推進求解的混合算法，選取2 維振蕩翼型非定常繞流、旋轉圓柱黏性繞流和模擬發動機槳葉旋轉運動的3 維懸停旋翼繞流進行考核運算，并與文獻計算或試驗結果進行比較分析。

1 控制方程

2 無網格/網格混合算法

2.1 無網格算法

2.1.1 空間導數擬合

計算域無網格布點離散后，形成點云結構，點云()由中心點及其周邊衛星點組成。空間導數基于當地點云逼近確定。沿用文獻[12]的做法，選用較為典型的加權最小二乘法，任一函數在點云中心點的1階擬合導數為

式中：α、β和γ為只與點云幾何位置信息相關的無網格系數；f為中心點與第個衛星點連線中點處的函數近似值。

2.1.2 空間離散

易于發現，式（1）與慣性坐標系下控制方程的主要區別在于包含矢通量、和的項及源項。對于前者，用式（3）可得

其中

分裂得到的L與在慣性坐標系下無網格算法對應的離散形式一致，可按慣性坐標系已有方法處理，最大程度地減少對已有慣性坐標系下無網格求解程序的改動。W在虛擬交界面上用中心格式確定， |中的速度分量則取為中心點和衛星點連線中點處的牽連速度分量。

源項中涉及的密度和速度等物理量直接取中心點處的值即可。式（1）中黏性矢通量部分的求解與慣性坐標系下的相同，其中的湍流黏性系數采用Spalart-Allmaras湍流模型計算，不再贅述。

2.1.3 時間離散

對式（1）進行空間離散后得到的半離散方程為

式中：R()為殘值，包含了對流矢通量、黏性矢通量和源項經空間離散后的部分。

對于非定常流動，式（8）可通過引入虛擬時間和非定常殘值，利用顯式雙時間步在虛擬時間層上推進，以求得下一物理時間步的解W。本文結合LU-SGS 格式形成隱式雙時間步推進算法。沿用Yoon等的思路，最終得到的2步推進格式為

式中：為對下一物理時間步守恒變量值W的逼近，即當虛擬時間層→時，有→W；()和()為點云中心點的衛星點集分割出來的2個子集。

需要注意的是式（12）中包含了源項產生的部分

上述算法將與網格算法集成，結合第2.3節中的跨區交界面處理技術，發展形成基于LU-SGS 隱式推進的無網格/網格混合算法。

2.2 邊界條件

以上的速度矢量均為絕對速度矢量。鏡像點處的壓強和密度取為對應原像點處的值。

遠場則基于帶源項的特征分析無反射邊界條件確定。

2.3 無網格/網格混合算法實施

計算域采用整體網格和物面附近局部無網格離散形成混合算法，實施的關鍵是無網格和網格分區交界面的處理。本文通過引入無網格和網格對偶點，實現了混合算法繞流信息的跨區交換。為了圖示清晰，以2維為例加以說明。對偶點一般取為交界面處2層網格的格點，如圖1所示。

第1 層稱為無網格對偶點（圖1 空心圓點），第2層稱為網格對偶點（圖1方點）。這些對偶點既被當做點云中的無網格點，也被當作網格單元的格點。作為前者時，純無網格點（圖1 實心圓點）和無網格對偶點周圍點云模板完整（圖1 虛線連接的點云結構），可用無網格算法計算；作為后者時，純網格節點和網格對偶點周圍網格模板完整（格點格式下），可用格點格式有限體積法求解。2 種算法均將物理量存儲于對偶點處，相互間可直接取用以實現跨區信息交換，無須插值。

由上述可知，采用原有方法挑選的對偶點，網格部分需要采用格點格式求解。而在求解非定常流動時需要額外的計算修正，涉及到所謂的質量矩陣運算。為了避免該問題，本文利用無網格取點的靈活性調整了對偶點的選取方法。將對偶點選取在網格區域靠近無網格區的若干層單元的中心，如圖2 所示（圖中各點含義同圖1）。

圖1 調整前選取的對偶點

圖2 調整后選取的對偶點

調整位置后，存儲于對偶點處的物理量亦可認為存儲于相應單元的中心，在計算時可被當作相應單元中心處的值直接取用，因此仍然無須插值便可實現跨區信息交換。但同時，除無網格對偶點所對應的單元外（網格模板不完整，但點云模板完整，使用無網格算法計算），其余網格均可統一采用格心格式的有限體積法統一求解，進而避免質量矩陣的計算。數值計算表明，上述處理方法能滿足跨區交界面數值通量傳遞的要求，表現為跨區等值線的連續（見第3.1節圖7）。

3 結果分析

本文對上述發展的混合算法編制了對應的計算程序，并進行了多個典型算例的考核運算。這里先給出NACA 0012翼型的俯仰振蕩非定常動邊界繞流和旋轉圓柱黏性繞流算例，再給出旋翼懸停飛行繞流算例。

3.1 NACA 0012翼型俯仰振蕩繞流

NACA 0012翼型俯仰振蕩繞流算例源自AGARD報告，其中翼型的俯仰可視為旋轉運動，已被許多文獻用于考核求解旋轉體繞流問題。初始時翼型位于平均攻角0.016°處，而后繞25%弦長點作俯仰振蕩，最大振幅對應攻角= 2.51°，來流馬赫數= 0.755，雷諾數= 5.5×10，試驗振蕩頻率= 62.5 Hz，攻角()隨時間變化為

計算采用的局部無網格區和網格區如圖3 所示。遠場邊界落在離物體10倍弦長處，涉及16320個無網格點和4331 個網格單元。為準確捕捉黏性流動的特征，物面附近的無網格區采用了沿法向的布點方式，第1層無網格點距離物面高度為1×10。

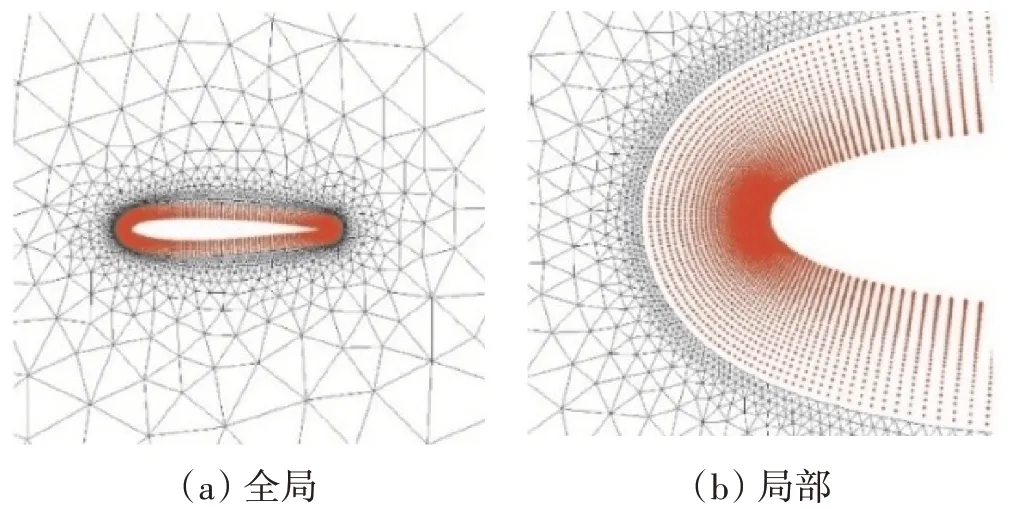
圖3 NACA 0012翼型周圍的無網格區和網格區

升力系數和力矩系數隨瞬時攻角的變化如圖4、5所示。從圖中可見遲滯環現象。圖4中的升力系數相對試驗值整體偏低，但與文獻中的計算值吻合得較好；對于力矩系數，所給結果只在個別試驗值處有較大偏差，但整體與試驗值和計算值都符合較好。4個典型時刻翼型表面的壓強系數分布如圖6所示，相應的試驗值也在圖中一并給出，供比較。不同時刻流場的壓強系數等值線如圖7 所示。展示出翼型俯仰振蕩時，激波等流場特征在翼型上下表面交替演化的情況。

圖4 升力系數隨攻角變化

圖5 力矩系數隨攻角變化

圖6 不同振蕩位置翼型表面對應壓強系數

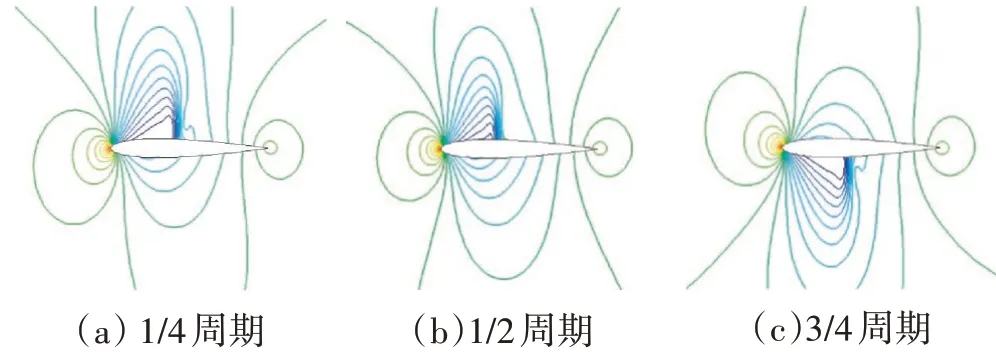
圖7 不同時刻流場的壓強系數等值線

3.2 旋轉圓柱黏性繞流

旋轉圓柱黏性繞流在增升減阻、改變旋渦釋放的規律、降低流動引起的振動等方面具有重要理論價值，歷來為流體力學學者所重視。Coutancea 等也對該流動現象進行了大量觀察和測量，為數值模擬提供了豐富的參考依據。這里給出本算例發展的算法獲得的運算結果。

設無窮遠處來流速度為，方向沿軸正向，圓柱直徑為，從靜止開始突然以角速度按逆時針方向旋轉，圓柱旋轉的角速度= 2。其中為轉速比，本文沿用文獻[21]取=0.5。來流條件為=0.1，=200。設無量綱時間=(，本文計算了∈[0,4]范圍內的流場情況。計算采用的無網格區和網格區如圖8所示。

圖8 圓柱周圍的無網格區和網格區

由于外形規則，網格區使用了4500 個結構網格單元，無網格區則填充了11476 個無網格點，遠場邊界落在離物體10 倍圓柱直徑處。物理時間步長取為總物理時長的1/800，即Δ=/800=/200。

不同無量綱時刻的計算流線和試驗流場照片如圖9 所示。從圖中可見，本文發展算法所得結果與試驗結果基本一致，表現在捕捉的旋渦在強度、位置等特征上與對應時刻試驗中觀察到的現象基本吻合。3 個無量綱時刻背風區上的方向速度分布如圖10 所示。從圖中可見，各時刻的速度分布曲線與試驗值均較為接近。

圖9 各時刻流線與試驗流場比較

圖10 背風區y = 0 上x 方向速度

3.3 懸停旋翼黏性繞流

懸停旋翼因繞固定軸旋轉，相當于發動機旋轉槳葉，因此，給出更具挑戰的3 維Caradonna 旋翼模型懸停飛行算例來模擬發動機旋轉槳葉繞流。該模型由2 片槳葉構成，槳葉平面呈長方形，展弦比為6。槳葉剖面為NA?CA0012翼型，沿展向無扭轉。計算狀態取為：槳尖馬赫數= 0.800（約2268 r/min），槳距角θ= 5°，雷諾數= 3.58×10。該旋轉引起的非定常流動在本文采用的旋轉坐標系下可視為準定常流動，因此，計算可按準定常進行。采用網格和無網格混合算法，計算區域離散整體用了235379 個網格單元和物面附近1200192 無 網格點，如圖11 所示。從圖中可見3 維Caradonna 旋翼模型和典型截面無網格和網格離散情況。為了準確捕捉黏性流動特性，法向第1 層無網格布點與物面距離為1×10，遠場落在離物體15倍的展向翼型弦長處。

圖11 旋翼表面及典型截面無網格和網格離散

在不同展向位置=0.50、0.68、0.80、0.96 的表面壓強系數計算值和試驗值比較如圖12 所示。從圖中可見，除了在個別點處與試驗值有所偏差外，計算結果與試驗值總體吻合，分布趨勢一致。

圖12 旋翼不同展向位置表面壓強系數

4 結論

（1）發展的混合算法是直接基于3 維旋轉坐標系下的N-S控制方程，相較于傳統的基于固定坐標系下的動網格算法，網格和局部無網格點云隨物體旋轉而無須重構，旋轉角速度等重要的特征物理量也無須插值運算，有效避免了因重構、插值等操作引起的誤差；

（2）混合算法繞流信息的跨區傳遞可利用無網格區點云取點的靈活性，借助于本文引入的無網格和網格對偶點實現。算例圖示等值線能跨區光滑過渡，證明本文發展的對偶點調整選取方法切實可行；

（3）發展的算法成功結合了LU-SGS 時間推進，并通過了模擬發動機槳葉旋轉運動的3 維懸停旋翼等典型復雜非定常繞流算例的考核運算，數值模擬結果與文獻計算或試驗結果吻合，展示出算法在模擬發動機槳葉等旋轉部件繞流問題方面具有重要的工程應用前景。