基于ADAMS的裝載機工作裝置動力學仿真方法研究*

楊思源 萬一品 宋緒丁

長安大學工程機械學院 西安 710064

0 引言

裝載機是工程建設中土石方施工的重要機種之一，可以對物料進行反復的鏟裝與運輸。對裝載機進行動力學仿真不僅可以縮短開發周期，還能夠降低開發成本。近年來，國內相關研究學者及企業設計人員對裝載機等工程機械裝備開展了許多動力學仿真與實驗研究工作。戴躍文等[1]對反轉六桿機構工作裝置進行了動力學仿真分析，并采用正交試驗的理論和方法對裝載機工作裝置進行了綜合優化設計。劉曉峰[2]利用ADAMS和Ansys建立了55 t汽車起重機柔性臂架系統，對其在多種工況進行仿真分析，得到臂架系統應力及振動情況，為臂架系統和液壓控制系統的設計提供依據。萬一品等[3]提出了三向力銷軸傳感器法和動臂截面彎矩法2種工作裝置載荷提取方法，并進行典型作業姿態下的載荷驗證，為載荷譜編制和疲勞特性分析提供依據。

以國產9 t裝載機工作裝置為研究對象，利用ADAMS的Step函數對其進行鏟裝模擬，得到各鉸點的峰值載荷以及各構件的最大應力的仿真方法。通過對其工作裝置的剛體動力學分析與基于實測數據的剛柔耦合動力學仿真分析，驗證了利用Step函數進行鏟裝仿真的合理性。為后續裝載機工作裝置的強度分析與結構優化提供參考依據。

1 工作裝置剛體動力學仿真

1.1 幾何模型與工作原理

以國產9 t裝載機為研究對象，建立其工作裝置三維幾何模型如圖1所示。

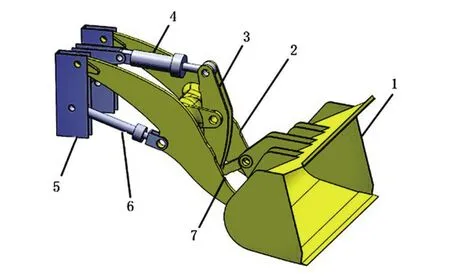
圖1 裝載機工作裝置三維模型

在實際鏟裝作業過程中，一個工作循環過程可分為典型的6個作業階段：插入階段、崛起階段、運輸階段、舉升階段、卸料階段以及復位階段[4]。在插入作業階段，鏟斗處于水平位置，動臂液壓缸伸長量最短且處于鎖死狀態，鏟斗一直向前插入物料最深處。在崛起作業階段，搖臂液壓缸伸長，將物料送入斗內，完成鏟裝作業。在舉升作業階段，搖臂液壓缸鎖死，動臂液壓缸伸長，將物料舉升直至卸料位置。在卸料作業階段，動臂液壓缸鎖死的同時搖臂液壓缸回縮，鏟斗翻轉，完成卸料作業。

由于物料的多樣性與分散性使得鏟裝作業過程中工作裝置受力特性復雜多變，測試每種物料的應力需要花費大量的時間、人力、物力，而通過虛擬樣機技術可快速獲得工作裝置各鉸接處的載荷。

1.2 載荷條件的確定

仿真分析時需要獲得裝載機工作裝置所受外力變化情況，給多剛體仿真模型中添加運動副及驅動函數來模擬鏟裝作業。裝載機作業期間，鏟裝作業段受力最為復雜，受到插入阻力、掘起阻力和物料重力的作用[5]。

插入阻力與物料種類、料堆高度等參數有關，其計算的經驗公式為

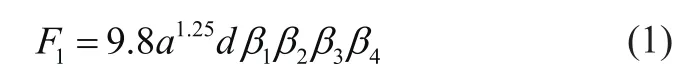
式中：F1為插入物料時鏟斗所受阻力，a為插入物料深度，d為鏟斗寬度，β1為物料松散度系數，β2為物料容積比系數，β3為物料堆高度系數，β4為鏟斗形狀影響系數。

掘起阻力計算的經驗公式為

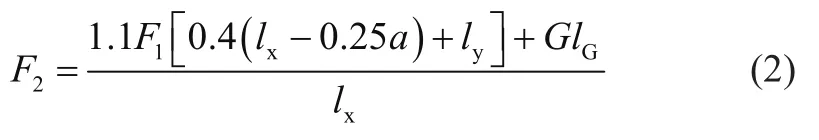
式中：F2為掘起阻力，lx為鏟斗斗尖端部到鏟斗與動臂鉸點的水平距離，ly為鏟斗斗尖底部到鏟斗與動臂鉸點到豎直距離，G為鏟斗與其所鏟裝物料的重力，lG為鏟斗質心到鏟斗與動臂鉸點的水平距離。

對各系數的取值進行選取，結合式(1)、式(2)以及工作裝置的參數可得到在鏟裝3.3 m左右高度的散狀物料時各工況下的插入阻力與崛起阻力，如表1所示。

表1 不同工況下的插入與崛起阻力 N

由表1可知隨著物料顆粒度的降低，插入阻力與崛起阻力均有所減小。

1.3 剛體動力學仿真分析

將工作裝置的幾何模型導入ADAMS中，如圖2所示。對機架進行固定約束，在各液壓缸體與液壓缸桿之間施加滑動副，在各鉸孔處添加旋轉副。

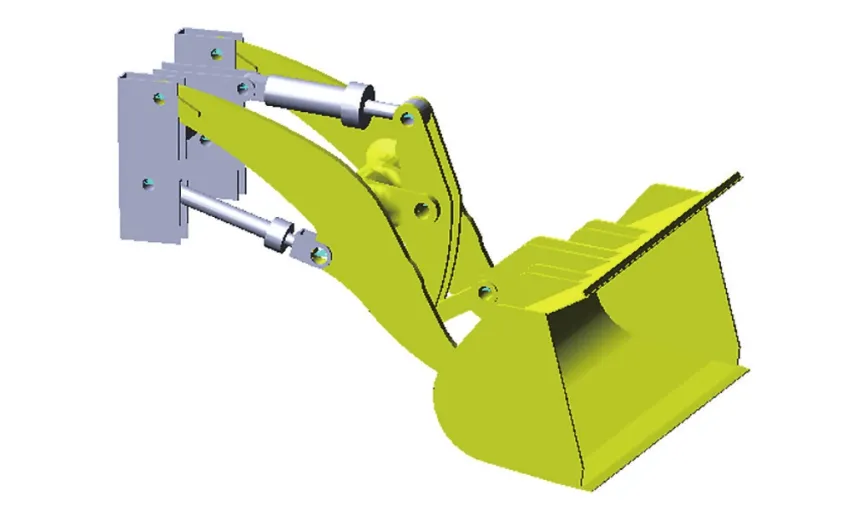
圖2 工作裝置剛體動力學模型

在模擬鏟裝作業時，在鏟斗中間位置施加插入阻力與崛起阻力，鏟斗首先插入物料最深，然后翻轉鏟斗完成鏟掘作業。仿真單位設置為MKS（m、kg、s），利用Step函數來添加鉸點載荷和液壓缸位移驅動，仿真時間設置為8 s。

在大石方工況下插入物料階段所受阻力的Step函數為

Step(time,0,0,2.8,- 401116) +Step( time,2.8,0,3,401116) +Step( time,3,0,8,0)

掘起物料階段所受阻力的Step函數為

Step( time,0,0,3,0) +Step( time,3,0,3.2,- 296209)

Step( time,3.2,0,6, 296209) +Step( time,6,0,8,0)

鏟斗內物料重力的Step函數為

Step( time,0,0,3.2,0) +Step(time,3.2,0,6,-88200)

+Step(time,6,0,8,0)

搖臂液壓缸位移的Step函數為

Step(time,0,0,3,0)+Step(time,3,0,6,-0.248)

+Step(time,6,0,8,0)

動臂液壓缸位移的Step函數為

Step( time,0,0,6,0) +Step( time,6,0,7,-0.045)

+Step( time,7,0,8,-0.06)

記動臂與鏟斗2個鉸點分別為A和鉸點B，連桿與鏟斗鉸點為C，由于在斗尖中點處施加載荷，且鉸點A和鉸點B呈對稱分布，所以鉸點A和鉸點B的載荷相同。分別輸出這3個鉸點在大石方與小石方工況下的載荷時間歷程如圖3所示。

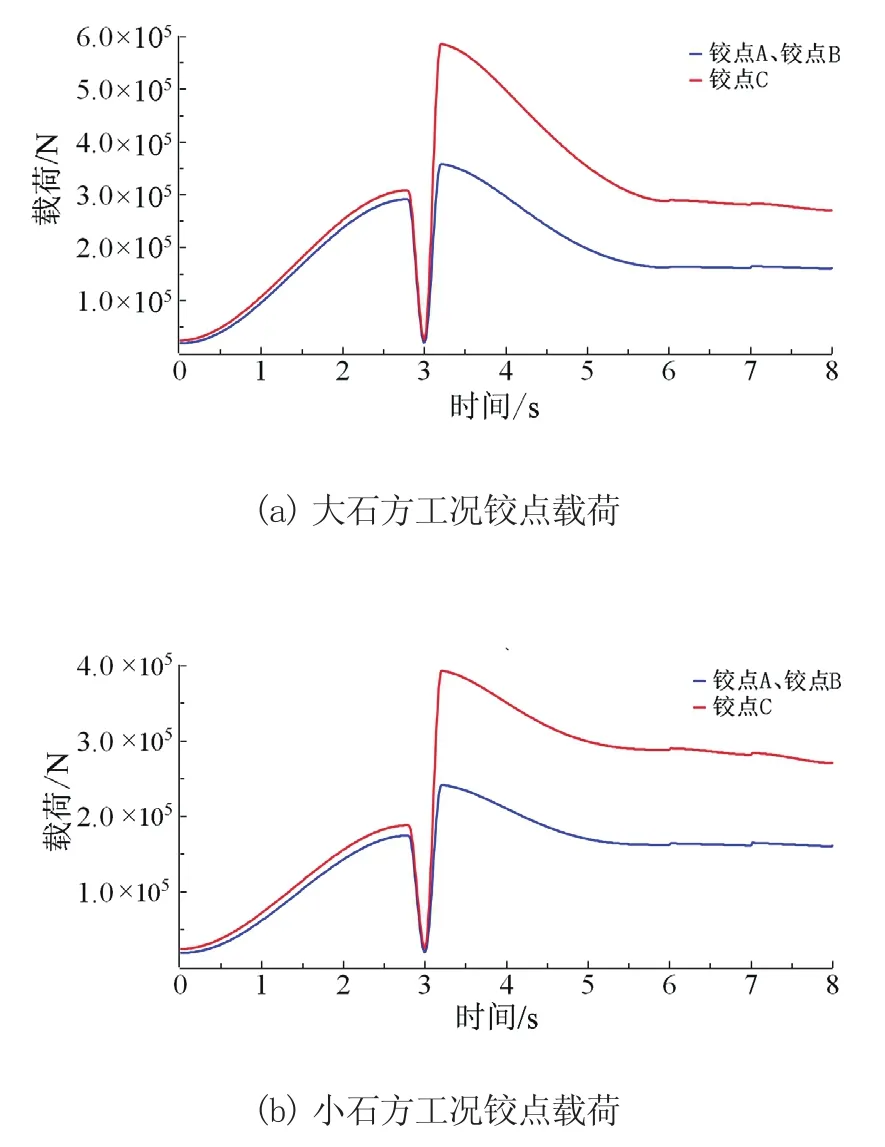
圖3 不同工況下各鉸點載荷

由圖3可知，3個鉸點的載荷呈現相同變化趨勢，第一峰值與第二峰值分別由插入阻力與掘起阻力引起。其中，鉸點C受力較大，在大石方與小石方工況下的峰值載荷分別為600 kN與400 kN。而鉸點A于鉸點B的載荷相對較小，在2個工況下分別達到358.44 kN與240.85 kN。2個工況下的實測鉸孔載荷如圖4、圖5所示。

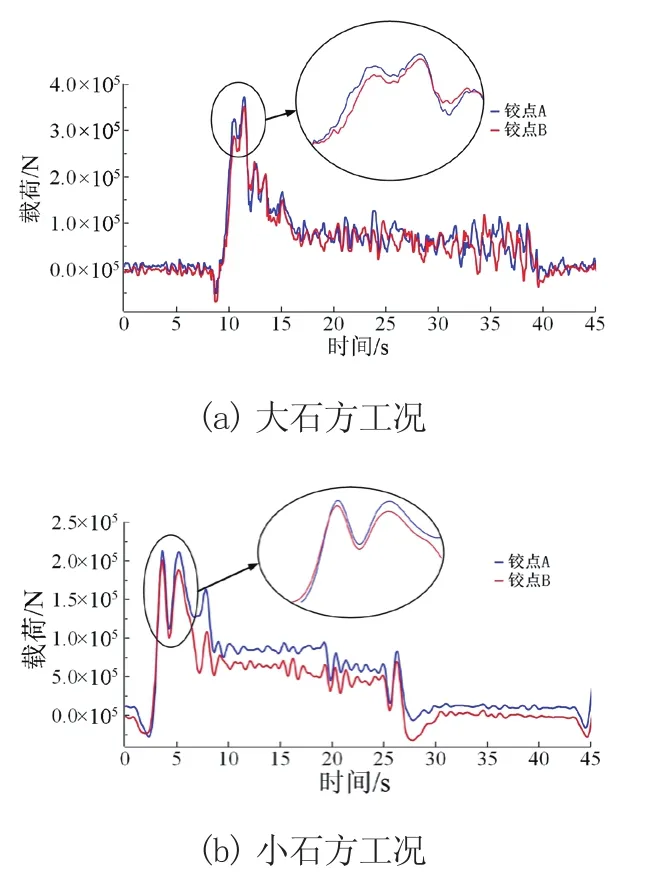
圖4 A和B鉸點實測載荷曲線

圖5 C鉸點載荷曲線

由圖4與圖5可知，在實際作業時鉸點A與鉸點B在不同的載荷大小有所區別，這是由于鏟裝物料分布不均勻所造成的偏載現象。其中鉸點A與鉸點B在大石方工況下的峰值載荷分別為373.20 kN和351.81 kN，在小石方工況下的峰值載荷分別為212.77 kN和200.88 kN。實測載荷與仿真結果對比如表2、表3所示。

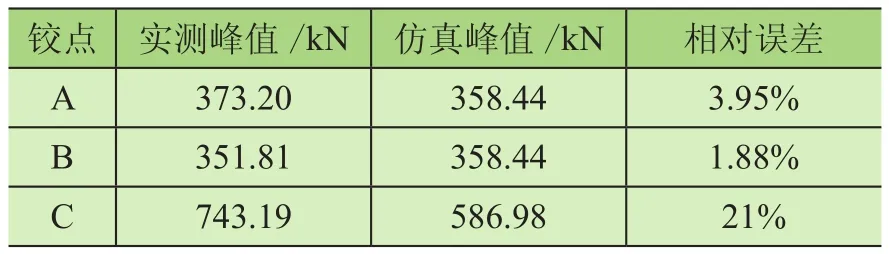
表2 大石方工況峰值載荷對比

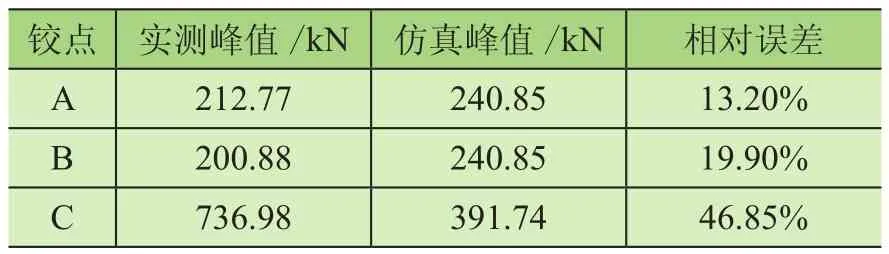
表3 小石方工況峰值載荷對比

由表1、表2可知，鉸點A和鉸點B的實測與仿真載荷峰值誤差不超過20%，雖然鉸點C的誤差較大，但連桿是二力構件，受力形式單一，且裝載機主要關注的受力部件是動臂，故通過動力學仿真可較好地反映動臂的受力情況。

2 工作裝置剛柔耦合動力學仿真

2.1 剛柔耦合動力學模型

仿真分析的結果受所建仿真模型的準確性影響。工作裝置在實際鏟裝作業過程中并不是純剛體，有必要研究剛柔耦合情況下工作裝置在鏟裝作業期間的受力情況。在實際工作中鏟斗的失效形式主要為磨損[6]，可將動臂、搖臂和連桿視為柔性體，動臂液壓缸、搖臂液壓缸、鏟斗以及機架仍視為剛性體，建立出與實際情況更為接近的仿真分析模型。

在工作裝置的動力學模型中引入柔性體，利用模態疊加法計算工作裝置在動力學仿真過程中的變形，可以提高動力學仿真的精度[7]。

將工作裝置三維模型導入Ansys中，創建單元屬性并定義材料為Q355鋼，然后進行網格劃分。在動臂、搖臂以及連桿鉸接處建立剛性區域，如圖6所示。

圖6 工作裝置剛性區域

提取各構件的前20階模態，采用Craig-Bampton模態綜合法來生成動力學分析所需的模態中性文件[8]。

用動臂、搖臂和連桿的模態中性文件替換剛性模型中的對應部件，建立裝載機工作裝置含有模態柔性體的剛柔耦合動力學模型，如圖7所示。

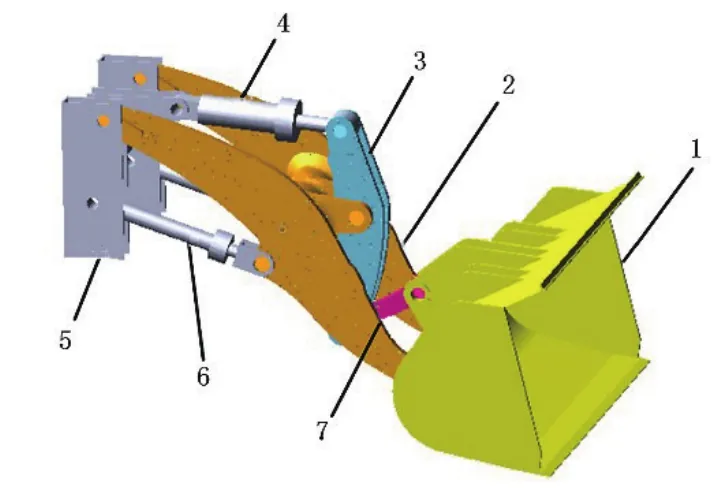
圖7 工作裝置剛柔耦合動力學模型

2.2 基于Step函數的剛柔耦合仿真

利用Step函數及相同的加載位置對工作裝置進行剛柔耦合動力學仿真。圖8為裝載機工作裝置在一個工作循環下應力最大時刻下的應力云圖。

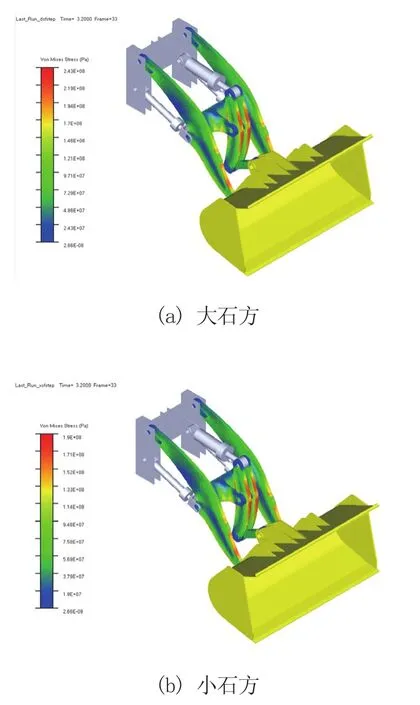
圖8 工作裝置應力最大時刻應力云圖

由圖8 可知，大石方與小石方工況下工作裝置最大應力分別為242.84 MPa和189.61 MPa，均發生在3.2 s，在動臂前端及搖臂前后端，由前文可知3.2 s正是掘起瞬間，受到掘起起阻力作用。

輸出各工況下最大應力時間歷程如圖9所示。

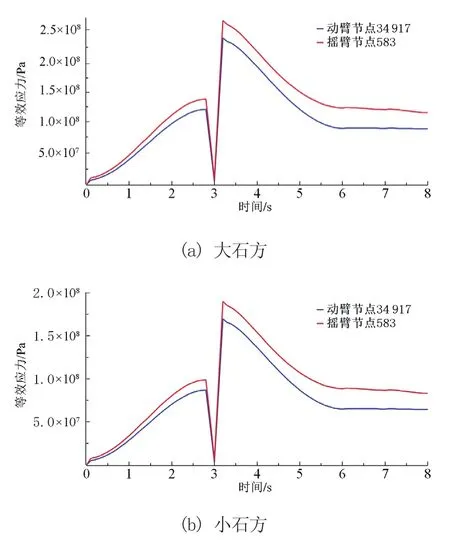
圖9 工作裝置應力最大節點應力時間歷程

2.3 基于實測載荷的剛柔耦合仿真

將大石方與小石方的實測液壓缸位移及鉸點載荷導入ADAMS生成樣條曲線，并將樣條曲線賦予相應的驅動與鉸點，大石方工況的實測液壓缸位移如圖10所示。

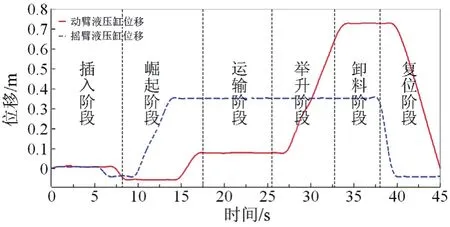
圖10 液壓缸位移曲線

經過仿真求解計算得到裝載機工作裝置最大時刻下的應力云圖如圖11所示。

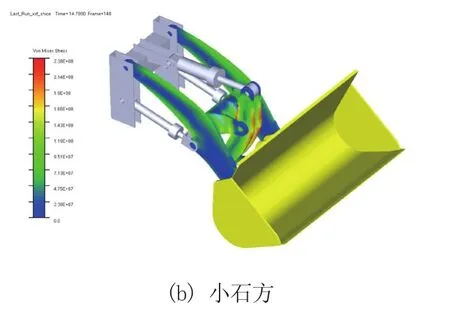
圖11 工作裝置應力最大時刻應力云圖

由圖11可知，在動臂后端與搖臂板前后端出現了較大的應力。輸出動臂與搖臂在兩工況下最大應力節點的等效應力時間歷程如圖12所示。

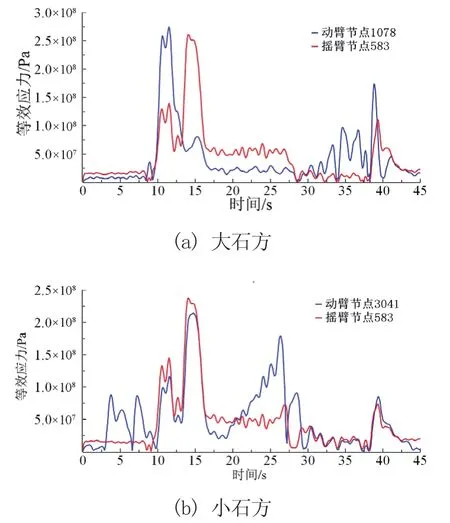
圖12 工作裝置應力最大節點應力時間歷程

分析圖12a可知在大石方工況下，動臂在插入階段末期所受應力最大，最大應力275.07 MPa，出現在11.5 s，而搖臂在掘起階段末期所受應力最大，最大應力為260.44 MPa，出現在14.0 s。在小石方工況下，動臂與搖臂均在掘起階段末期14.7 s出現最大應力，最大應力分別為213.79 MPa和237.70 MPa。基于實測載荷與Step函數仿真的工作裝置峰值應力結果對比如表4所示。

表4 峰值載荷對比

由表4可知基于Step函數仿真應力結果與基于實測載荷的仿真應力結果相對誤差不超過26%，因此通過Step函數模擬工作裝置鏟裝作業可較好地反映工作裝置的應力大小。

4 結論

1）對額定載重9 t裝載機的工作裝置采用Step函數進行剛體動力學仿真，提取鉸點載荷并與實測載荷對比，發現兩者的峰值載荷相對誤差不超過20%，驗證了利用Step仿真的合理性。

2）建立工作裝置的剛柔耦合模型，分別采用Step函數和實測數據進行剛柔耦合動力學仿真，結果表明，2種仿真方法之間的峰值應力的相對誤差不超過26%，驗證了Step函數仿真方法的正確性

3）通過仿真分析發現搖臂所受應力較大，應對其進行結構加強改進，以提高其強度。