基于線性調頻信號二次相位變換的主動聲吶目標速度估計

顧怡鳴，宮在曉，李整林

(1. 中國科學院聲學研究所聲場聲信息國家重點實驗室，北京 100190；2. 中國科學院大學，北京 100190)

0 引 言

線性調頻(Linear Frequency Modulation, LFM)是主動聲吶常用的探測信號，通過分析 LFM 信號目標回波可估計目標與探測平臺的相對速度。傳統的LFM測速方法主要有多普勒頻移補償法和組合脈沖法。多普勒頻移補償法利用長脈寬 LFM 信號的多普勒敏感性，對探測信號進行多普勒頻移搜索來估計相對速度[1]。組合脈沖法利用LFM信號模糊函數的時延-多普勒耦合性，通過正負調頻信號匹配濾波峰值的時延差估計速度，也被擴展應用于雙曲調頻信號[2]。但主動聲吶的發射占空比通常較小，組合脈沖增加了信號的發射周期。

分數階傅里葉變換(Fractional Fourier Transform, FrFT)是一種時頻旋轉變換，近年來已經被廣泛用于 LFM 信號的檢測和參數估計[3-13]。文獻[14]首先將 FrFT應用于主動聲吶回波檢測，并利用海上實驗數據證明了 FrFT在混響背景下可以獲得比匹配濾波器更高的信噪比和速度估計精度。但FrFT較高的計算復雜度限制了其實際應用，針對該問題，學者們提出了一些快速 FrFT算法[15-21]。采樣型算法對時間和頻率進行尺度歸一化，可以借助快速傅里葉變換(FFT)算法極大地降低計算量[15-16]；特征向量分解型算法[12-13]通過設計離散傅里葉變換矩陣求解對應的特征向量；文獻[21]中利用莫比烏斯反演公式證明了分數階傅里葉級數的存在，并以此為基礎提出了低復雜度的離散FrFT算法。FrFT方法檢測 LFM 信號主要利用了其解調頻的性質，舍棄一些冗余的性質，對變換形式進行簡化以降低計算量，例如二次相位變換[22-24](Quadratic Phase Transform, QPT)或簡明分數階傅里葉變換[7-8]，以及具有高次變換核的多項式時頻變換[25-26]。

現有的 FrFT估計速度方法需要對變換參數進行搜索，在自主水下機器人(Autonomous Underwater Vehicle, AUV)等計算力有限的平臺難以實時處理。本文針對該問題提出了一種基于二次相位變換的線性調頻信號速度估計方法。QPT參數失配時能量無法聚焦，幅度譜存在一定展寬。本文推導了 QPT參數與信號參數失配時變換域幅度譜的解析解，分析了二次相位變換幅度譜展寬與多普勒頻移之間的關系，提出了利用單次QPT后幅度譜寬度的速度估計方法。基于單個線性調頻信號進行QPT后幅度譜的展寬信息實現了目標相對速度估計，避免了對變換參數的掃描，減少了一個維度的計算量。針對單次QPT結果無法確定速度符號的問題，提出了對稱參數QPT符號判斷方法。通過數值仿真驗證了方法的有效性，并與 FrFT參數掃描方法進行了對比。

1 FrFT測速方法

FrFT的變換參數cotα與信號的調頻斜率k匹配時，變換核中的 ( t2/2)cotα項對信號實現解調頻，變換結果的幅度取得最大值。文獻[14]依據該性質給出了通過掃描 FrFT變換參數搜索最大峰值的測速方法。以長度為20 s、頻帶400～500 Hz的LFM信號為例，根據式(5)得到FrFT對LFM信號u-多普勒模糊(見圖1)。由圖1可以看出，當變換參數與信號速度匹配時變換結果的幅度取得最大值。FrFT測速方法的原理是在變換域-多普勒平面內搜索最大值，找到最大值對應的變換參數，進而通過變換參數與多普勒頻移之間的關系得到目標相對速度的估計值。

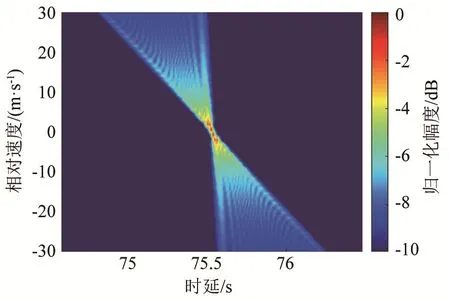
圖1 FrFT對LFM信號的u-多普勒模糊圖Fig.1 Schematic diagram of the u-Doppler ambiguity of FrFT for LFM signal

2 QPT速度估計方法

2.1 參數失配時LFM信號的QPT

二次相位變換可以看作是 FrFT的簡化，信號x(t)的QPT定義為[25]

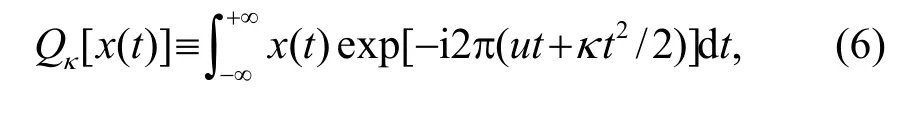
其中，u和κ是變換參數。當變換參數和線性調頻信號的調頻斜率k匹配，即k =κ 時，信號能量會在變換域聚集為峰值，此類情況已經在現有文獻中廣泛討論；當變換參數與信號參數失配時k≠κ ，信號的能量在變換域表現為一定展寬，已有文獻尚未發現有關變換參數與信號參數失配時特征的研究。以下給出變換參數與 LFM 信號調頻斜率不匹配情況下變換結果的解析解。

多普勒頻移后的回波信號二次相位變換可表示為

變換后信號的幅度譜由兩種形式的 Fresnel積分(如圖2所示)決定，式(10)對應的幅度譜大部分區域為零，如圖3所示，能量集中在一定的寬度，定義幅度譜寬度Bα為幅度譜峰值-3 dB對應的u域寬度，能量集中的范圍的寬度為

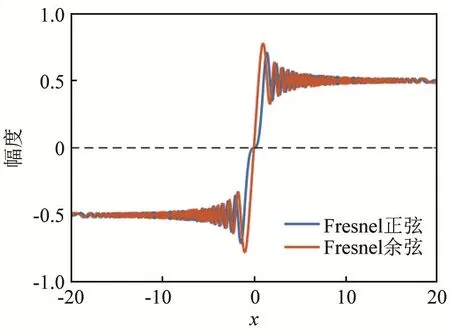
圖2 宗量為x的Fresnel積分Fig.2 Fresnel integral with argument x

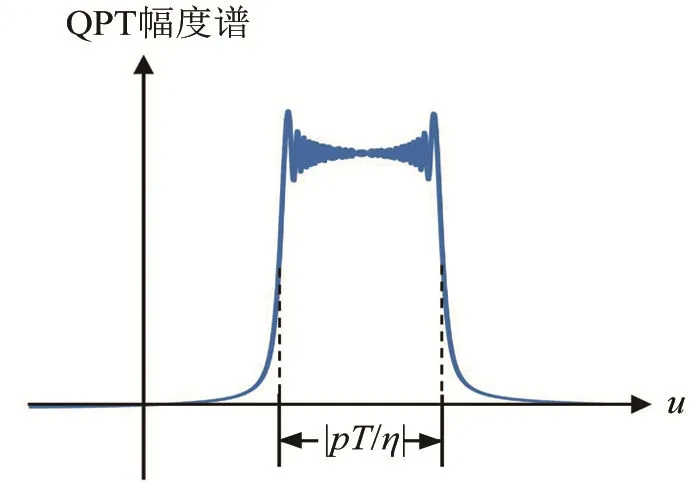
圖3 多普勒頻移后的回波信號QPT的幅度譜示意圖Fig.3 QPT amplitude spectrum of the echo with Doppler frequency shift

2.2 單次QPT速度估計方法

以上推導表明，參數失配時LFM信號QPT的幅度譜寬度與信號多普勒頻移存在確定關系，利用該特征可估計目標相對速度。若變換參數為原始信號參數時κ= k，LFM信號QPT的幅度譜的寬度為

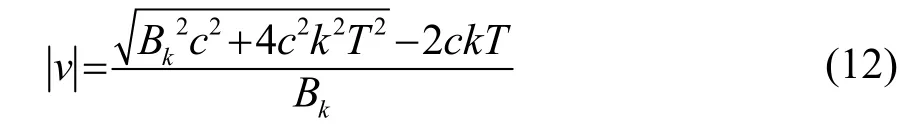
式中：c為聲速；k和T為LFM信號的調頻斜率和脈沖寬度。只需要通過估計幅度譜寬度Bk即可得到相對速度。QPT幅度譜的寬度信息可通過閾值檢測獲取，即：

其中：d為檢測門限，根據閾值檢測幅度譜的前后沿u0和u1可估計幅度譜寬度的估計值目標靜止時QPT幅度譜為sinc函數，幅度譜寬度為。需要注意的是，式(10)并不是完美的矩形窗函數，檢測門限較高時估計的寬度會偏小，需要通過修正系數進行補償。

根據 QPT幅度譜的寬度可以估計相對速度 v的大小，相對速度的符號則可以根據幅度譜前沿與的關系來確定：

假設 LFM 信號長度為 20 s，頻帶 400～500 Hz，對相對速度為 0和 30 m·s-1的信號進行QPT后得到的幅度譜分別如圖4(a)和圖4(b)所示，可以看出，當相對速度為0時，信號能量在變換域聚焦，信號QPT幅度譜幾乎沒有展寬。相對速度為30 m·s-1時，信號QPT幅度譜展寬明顯，并且與式(11)理論分析的寬度一致。圖4(c)為QPT對LFM信號u-多普勒模糊，可以看出，隨著相對速度的增加，QPT幅度譜逐漸展寬。同時，當相對速度為正時，幅度譜分布位于f0- kτ0右側，相對速度為負時位于f0- kτ0左側。由于信號的能量一定，QPT幅度譜的幅度隨展寬而降低。經過閾值檢測后的寬度圖像如圖4(d)所示，根據寬度可以進一步估計目標相對速度。需要注意，單次QPT方法依賴式(14)判定速度的正負，實際應用中不能準確獲取時延τ0，因此單次 QPT提供的信息在判斷速度的正負方面存在缺陷。

圖4 單次QPT的速度估計方法Fig.4 Velocity estimation method with single QPT

2.3 對稱參數QPT速度符號判斷方法

單次 QPT譜寬度僅提供了相對速度的大小信息，不能確定相對速度的符號，這里給出對稱參數QPT速度符號判斷方法。圖 5為符號判斷方法的示意圖，給定一個初始寬度B0，若信號不存在多普勒頻移時，B0對應的兩組變換參數分別為分別對回波信號進行變換參數為κ+和κ-的 QPT，分別可以得到兩組變換的幅度譜寬度Bκ+和Bκ-，兩次對稱參數 QPT幅度譜寬度為

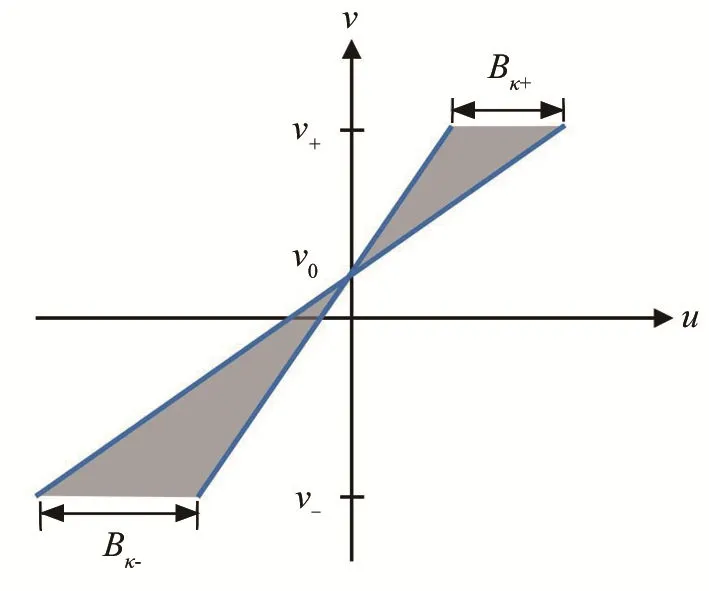
圖5 對稱參數QPT速度符號判斷示意圖Fig.5 Schematic diagram of speed symbol judgment with symmetrical parameter QPT

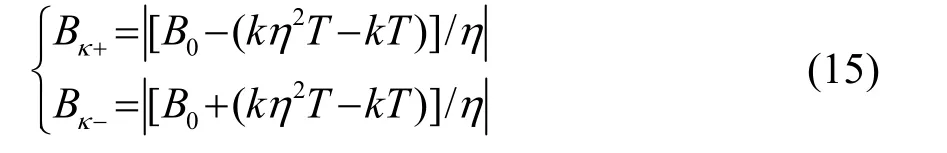
由式(15)可以看出，當信號相對速度為正時，伸縮因子η＞ 0，Bκ+＜ Bκ-；當信號相對速度為負時，伸縮因子η＜0，Bκ+＜ Bκ-。通過對比兩次對稱參數QPT幅度譜寬度可判斷相對速度的符號。

3 仿真實驗與性能分析

本節通過數值仿真實驗驗證 QPT速度估計方法的有效性，并將QPT方法與FrFT參數掃描方法的性能進行對比。仿真環境為無限空間，海水聲速為 1 500 m·s-1。仿真實驗的部署如圖 6(a)所示，藍圈靜止位于坐標原點(0, 0)的收發合置的主動聲吶平臺，黑圈代表目標起始位置(-10 km, 5 km)，虛線代表目標自東向西以速度 200 m·s-1勻速運動的航線。根據目標運動速度和相對平臺的方位可以得到目標與平臺的相對速度如圖6(b)所示，正速度表示目標接近平臺。探測信號為長度 20 s、頻帶 400～500 Hz的LFM信號，信號發射周期為60 s。在整個20 km的運動距離內，總計發射16個脈沖。

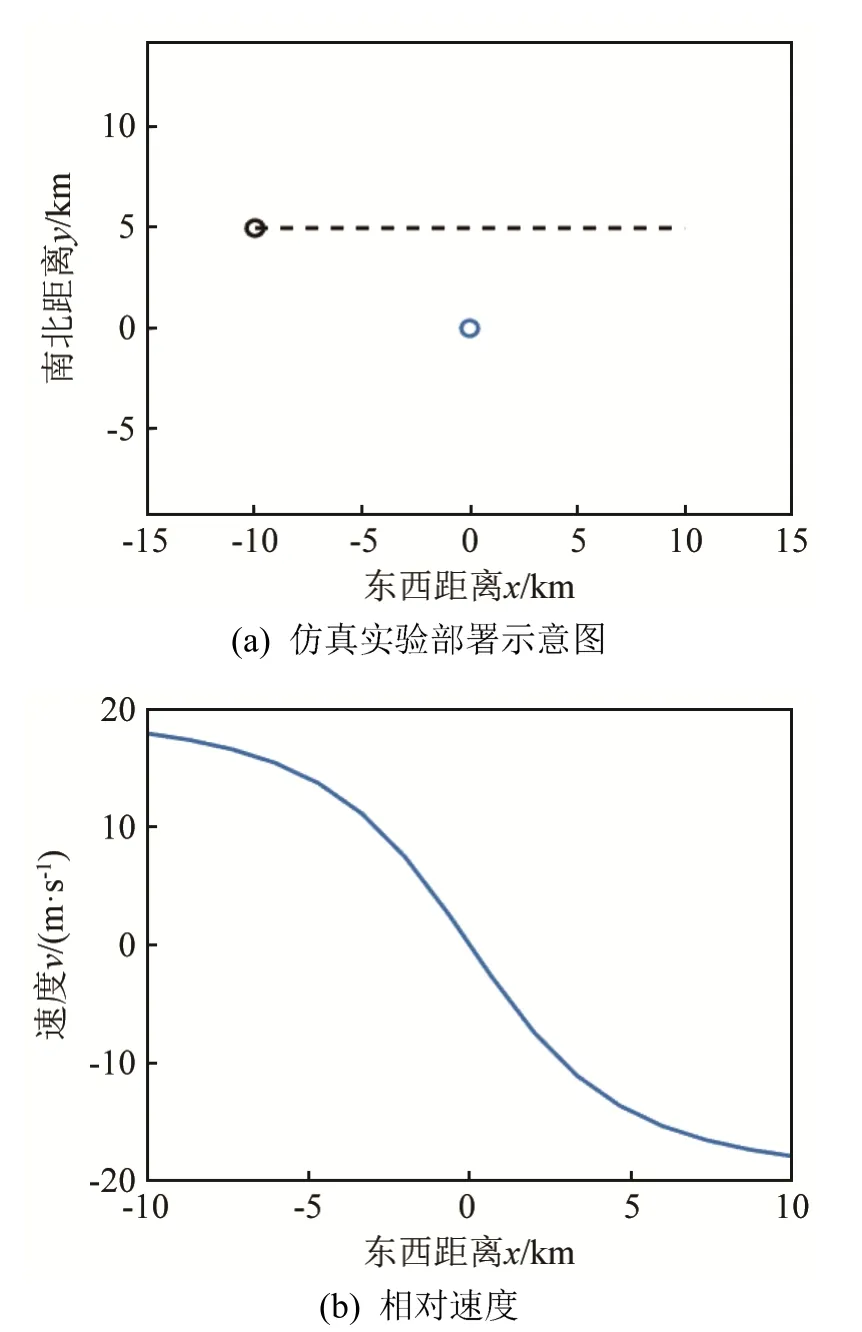
圖6 仿真實驗部署Fig.6 Deployment of simulation experiment

仿真接收信號的采樣頻率為5 000 Hz，假設背景噪聲為高斯白噪聲，回波信號頻帶內的信噪比為20 dB。仿真回波信號直接經過QPT后的幅度譜如圖7(a)所示，回波QPT后幅度譜能量集中的位置與回波的時延有關。為了更加直觀地表現相對速度對 QPT幅度譜的影響，將 u坐標變換為u′坐標，結果如圖 7(b)所示。對比真實相對速度(圖 6(b))可以觀察到 QPT幅度譜寬度與相對速度大小的對應關系，設置檢測門限為，進行寬度檢測并依據式(12)的函數關系即可估計目標的相對速度。圖8為對稱參數QPT得到的幅度譜寬度檢測結果，其中藍線和紅線分別對應正參數和負參數變換對應的幅度譜寬度，通過對比兩者之間的大小可以判斷速度的正負。

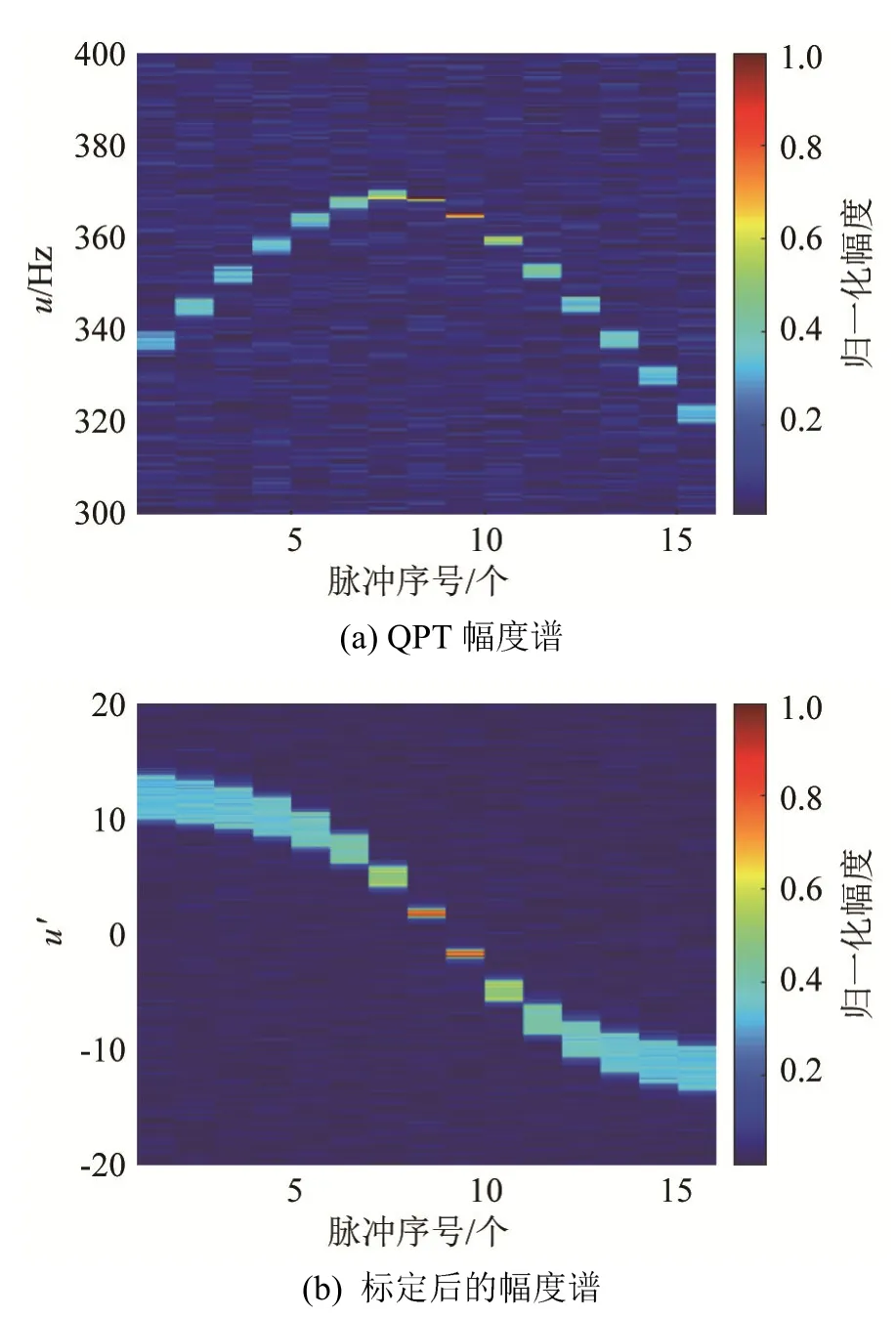
圖7 仿真數據QPT譜寬度估計Fig.7 Estimation of the of QPT spectrum width of simulation data

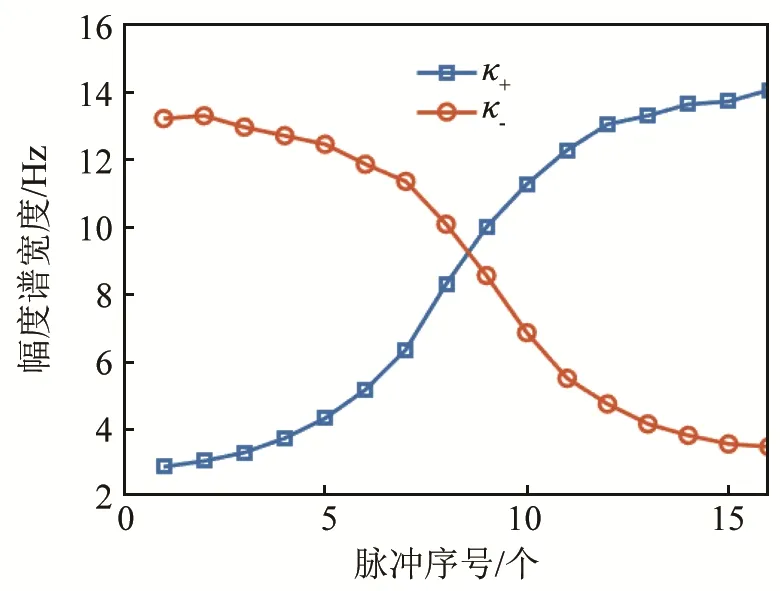
圖8 對稱參數QPT幅度譜寬度估計結果Fig.8 Estimation of the amplitude spectrum width by using QPT of symmetric parameters

在實際應用中，FrFT測速方法不需要對0～π所有的變換參數進行搜索，通過速度和變換參數的關系限定參數掃描的范圍可以降低計算量。速度掃描范圍確定后，計算量與掃描的分辨率相關，掃描分辨率也直接決定了 FrFT方法的速度估計精度。仿真中，FrFT方法的速度掃描范圍限定在-30～30 m·s-1范圍內，掃描間隔分別采用3、1和0.3 m·s-1，對應的FrFT點數Nα分別為10、60和100點。分別利用 FrFT和 QPT兩種方法對相對速度進行估計，得到速度誤差如圖9所示。由圖9可以看出，FrFT方法的速度估計精度主要與參數掃描的分辨率有關，仿真數據單次QPT方法的速度估計精度基本可以保持在1 m·s-1以內，與60點的FrFT方法精度相當。

圖9 FrFT參數掃描方法與單次QPT方法速度估計誤差對比Fig.9 Comparison of velocity estimation error between FRFT parameter scanning method and QPT method

FrFT類算法的計算復雜度分析在許多文獻中已有討論[7-8,15,26]，盡管QPT簡化了變換核，但計算復雜度仍與 FrFT的量級相當。忽略計算復雜度的低階項，兩種變換基于 FFT的快速算法計算復雜度量級均為O(NlgN)，其中N表示單次處理的時域數據點數。遠程主動探測回波處理的時間窗較長，處理點數的增加使算法的時間復雜度急劇上升。以第2節仿真實驗中采用的參數(窗長度40 s，采樣點數20 000點)為例，評估不同參數掃描量的計算量，結果如圖10所示，Nα=1對應的虛線表示單次QPT的計算量。如果只估計相對速度大小，QPT計算量僅為精度相當的FrFT方法的1/60；增加判斷相對速度符號，則計算量為FrFT方法的1/30。

圖10 不同參數掃描量的計算量估計Fig.10 The computational costs of different scanning parameters

參數失配時能量在變換域并非聚焦于一點，因此 QPT方法的抗噪聲性能差于 FrFT參數掃描方法。假設回波信號的帶內信噪比為 20 dB，不同相對速度回波信號的QPT幅度譜波形如圖11所示，相對速度為0時，信號能量完全聚焦，背景起伏很低，隨著相對速度提高，背景起伏逐漸升高。定義峰值信噪比為輸出信噪比，通過 20次蒙特卡洛仿真估計QPT和FrFT兩種方法的輸出信噪比隨相對速度的變化，結果如圖12所示，藍線和紅線分別表示QPT方法和FrFT方法的輸出信噪比。可以看出，QPT方法的輸出信噪比在相對速度為0時輸出信噪比與FrFT方法相同，隨著目標相對速度提高，信號能量在變換域逐漸分散，輸出信噪比逐漸降低。上述數值分析表明，QPT方法的抗噪聲性能比FrFT方法差，該方法計算效率提高的代價是輸出信噪比的降低。雖然經典的 FFT譜分析方法通過分析信號頻偏也可獲得目標速度，但主動聲吶接收的目標回波信號通常信噪比很低，FFT完全無法聚焦信號的能量，輸出信噪比遠低于以上兩種方法。

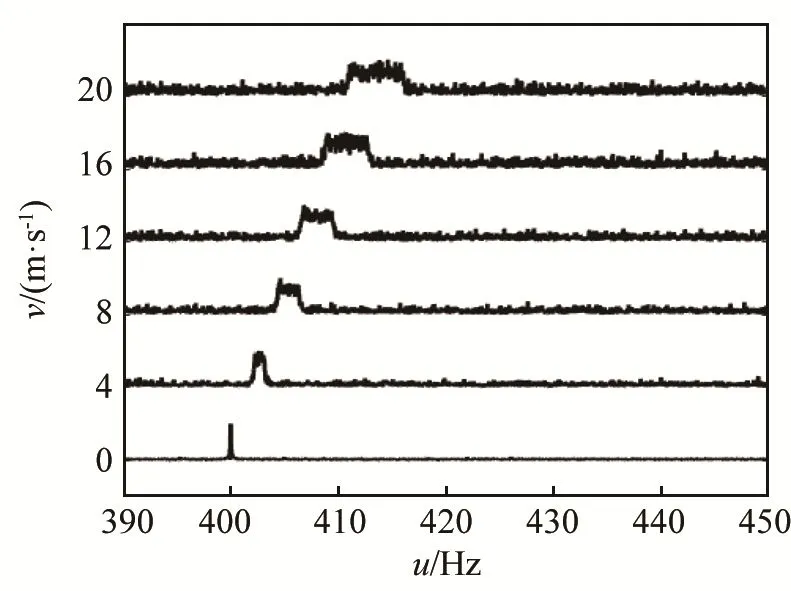
圖11 不同相對速度QPT幅度譜的波形Fig.11 Waveforms of QPT spectrums corresponding to different relative velocities

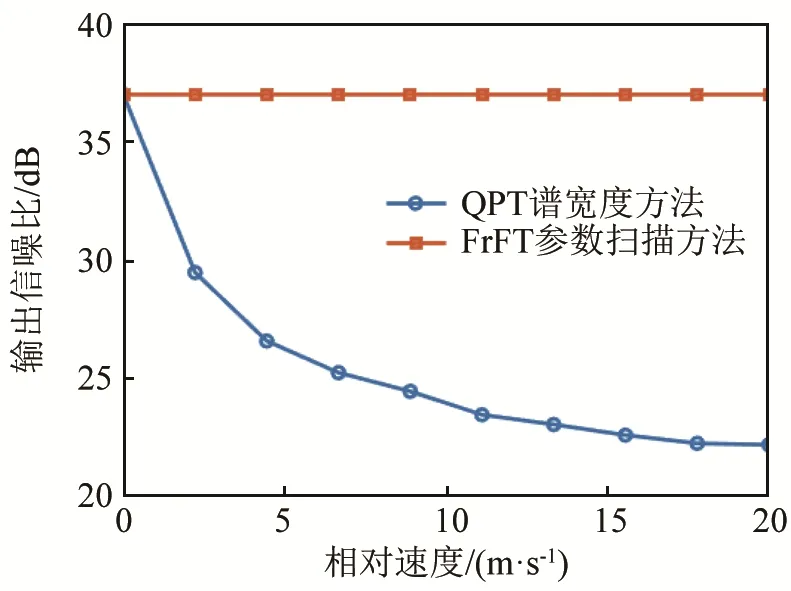
圖12 QPT方法和FrFT方法的輸出信噪比對比Fig.12 Comparison of output signal to noise ratio between QPT method and FrFT method

4 結 論

本文提出了一種基于二次相位變換的主動聲吶線性調頻信號的速度估計方法，通過減少變換次數降低了 FrFT類算法速度估計的計算量。單次QPT速度估計方法利用LFM變換后幅度譜寬度與信號多普勒頻移的關系對速度進行估計，速度符號的判斷依賴準確的到達時刻。針對實際情況下難以準確估計時延的問題，提出了對稱參數QPT速度符號判斷方法，通過對比對稱參數變換的幅度譜寬度判斷速度符號。由于不需要對變換參數進行搜索，相較于 FrFT參數掃描的方法，所提速度估計方法可以降低一個維度的計算量。仿真實驗結果表明，該方法的速度估計精度可以達到1 m·s-1，如果只估計相對速度大小，計算量僅為精度相當的FrFT參數掃描方法的1/60。但該方法計算效率提高的代價是輸出信噪比的降低，在實際應用中需要進行權衡。考慮到復雜海洋環境條件下主動聲吶接收回波信號存在畸變，本文的方法還有待復雜信道下真實主動聲吶實驗數據的驗證。