固體中二維縱波非線性方程的攝動解

錢昕彤，韓慶邦，蘇娜娜，錢佳文，柏 樂，單鳴雷

(河海大學物聯網工程學院，江蘇 常州 213022)

0 引 言

大振幅聲波在固體材料中傳播時，與該固體介質相互作用，會產生波形畸變、聲飽和、聲波與聲波非線性相互作用等一系列的非線性現象[1]。例如，聲波在傳播過程中會產生高頻聲波信號，其頻率往往是原始信號的整數倍，這種現象被稱為高次諧波現象。此時，線性聲波的疊加定理不再適用，需要對固體中非線性聲波特性進行研究，而研究非線性聲波方程是常見的研究思路之一。基于固體中的彈性波理論，Landau等[2]和 Murnaghan[3]很早就研究了固體介質中的非線性聲學問題，得到了各向同性介質中的非線性聲波方程。研究表明此類非線性聲波方程可以很好地描述聲波在非線性固體材料中的傳播特性[4]。對固體中非線性彈性波特性的研究，此類問題歸結于經典非線性問題，是非線性聲學研究及應用的理論基礎。

目前，關于此類非線性聲波方程的研究大多聚焦于一維情況。已有研究者通過采取不同的方法對此類非線性聲波方程進行求解，得到了不同形式下的一維非線性聲波的解析解[5-6]。由于固體中的非線性聲波方程十分復雜，很難得到精確解，而攝動法是解決此類非線性問題的常用方法之一，通過對方程進行相應的攝動展開，常常可以得到具有相應精度的解析解。因此，部分研究者采用攝動法求解得到方程的近似解[7-9]。張世功[10]利用攝動法對縱波激發與橫波激發兩種情況下的一維非線性方程進行了詳細求解。吳先梅等[11]對非線性縱波方程進行三階攝動展開，得到了非線性縱波方程的三階攝動解。呂文翰等[12]圍繞聲馬赫系數對一維非線性方程的解進行攝動展開，從而得到了高階攝動解。He[13-14]基于同倫攝動法對多種非線性方程進行了詳細求解，這種新方法可以很好地得到非線性方程的攝動解。Ezzati等[15]基于He的研究，利用同倫攝動法求解非線性波動方程，進一步提升了求解精度。上述研究者對此類一維非線性聲波方程進行攝動近似求解，并得到相應的解析解。但對于更復雜的高維度的問題，人們暫時還沒有更好的研究方法。

非線性聲學方法在微損傷檢測中的應用，此類問題歸結為非經典非線性問題[16]，主要研究由微小缺陷(早期位錯疲勞損傷、疲勞微裂紋、不完美界面等)所引起的聲學非線性效應。大量研究者針對此類問題進行了深入的研究。Qian[17]深入研究了P波、SV波和SH波斜入射情況下的二階聲場，利用勢函數的表示方法對二維聲波方程進行詳細求解。一些研究者基于二維非線性方程探究非線性縱波的斜入射的問題。Biwa等[18]建立固-固界面的彈簧模型，對聲波斜入射情況下的二階聲場特性進行詳細研究。Shirgina等[19]針對四種不同類型的界面層，探究斜入射縱波產生的非線性諧波的反射傳播特性。Wu等[20]基于錢祖文的研究對P波斜入射于固-固界面的二階諧波場特性進行了詳細描述。聲波在有微小缺陷的固體材料中傳播，所產生的非線性現象是由固體介質的材料特性和固體微小缺陷共同貢獻的。上述研究者在研究固-固界面的非線性問題時，重點關注聲波在固體介質中傳播時由固體缺陷產生的非線性現象。而在此基礎上進一步考慮聲波與固體材料相互作用而產生的非線性影響，可以得到更加精確的結果。相關內容還未在相關文獻中呈現，這對于固體中的非線性超聲評估研究而言仍是一個值得關注與研究的問題。因此，有必要對二維固體中非線性彈性波的特性進行相應研究，即研究二維非線性聲波方程的非線性問題。

Alkhalifah[21]利用縱波方程代替彈性波方程，并將微擾理論應用于求解各向異性的縱波方程中，以描述縱波斜入射所產生的縱波場。該方法通過引入一個遠小于1的無量綱小參數作為攝動量，采用泰勒展開的方式對方程的解進行微擾展開，最終得到相應的解析解。基于上述研究方法，本文選取聲馬赫數作為微擾小項，圍繞其對二維非線性聲波方程的解進行攝動求解。

本文從二維非線性縱波方程出發，圍繞聲馬赫數對該方程的解進行二階攝動展開，從而求解出二維非線性縱波方程的二階攝動解。考慮到在實際測量情況下，單個探頭單次只能測量某一方向的聲波信號。因此，根據計算結果定義了兩個非線性系數(二次諧波沿x軸傳播分量A1x和沿y軸傳播分量A1y與入射基波A0的振幅比)，利用數值計算的方法探究影響非線性系數的因素，從而探尋二維非線性縱波及其二次諧波的傳播規律。

1 二維縱波非線性方程的攝動解

為探究某一特定方向上二維縱波傳播時的非線性，對其沿坐標軸進行了相應分解。建立如圖 1所示的聲波傳播模型，二維縱波在具有各向同性的固體材料中傳播。

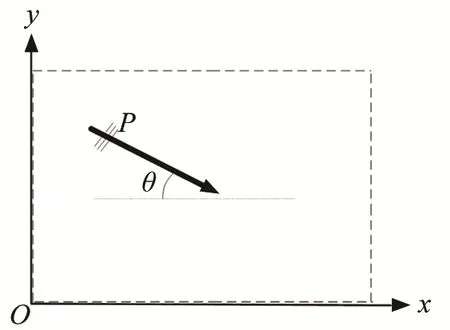
圖1 二維縱波在固體介質中傳播的示意圖Fig.1 Two-dimensional longitudinal wave propagation in solid media

圖1中，虛線所圍成的長方形表示固體介質。二維縱波P以入射角θ斜入射于固體材料，并在固體中傳播。當θ=0°時，表示二維縱波沿x軸方向入射，當θ=90°時，表示二維縱波沿y軸方向入射。

根據Murnaghan參數[3]推導的固體中的二維縱波方程，如式(1)、(2)所示：

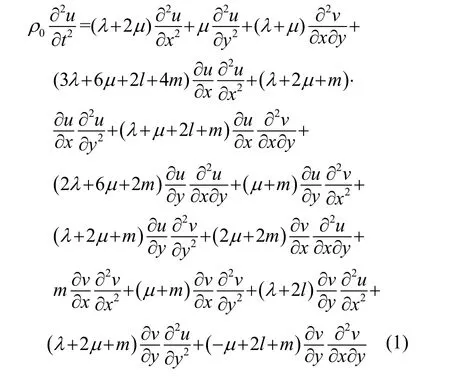
其中， u = u ( x, y, t )和v= v ( x, y, t)分別表示二維縱波沿x軸方向傳播的位移分量和沿y軸方向傳播的位移分量；ρ0為固體材料的密度；λ、μ為 Lame常數；l、m為Murnaghan參數。

攝動法是求解非線性方程近似解的常用方法之一。其主要思想是將方程中的非線性因素視為對方程中線性部分的一種微小擾動，基于線性解尋求方程的近似解。在利用攝動法求解方程的過程中常常需要引入與方程中物理量相關的無量綱小參數作為攝動量，且其值應遠小于 1。因此，本文選取聲馬赫數Ma作為攝動小項，Ma的計算公式為

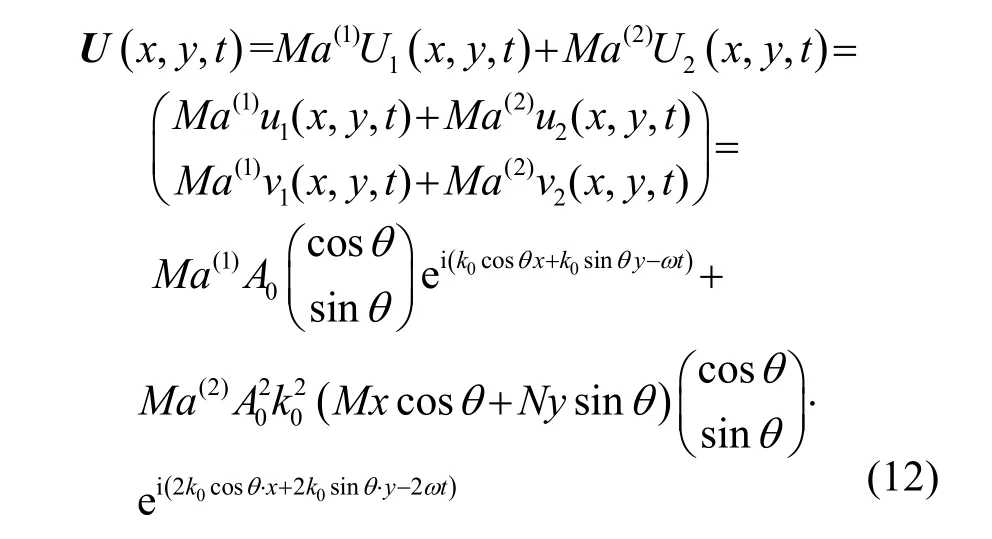
最終得到的式(12)即為二維縱波非線性波動方程(1)和(2)的攝動解。

2 數值計算與結果分析

根據式(12)中的二維縱波非線性方程的攝動解可知，二維縱波在固體中傳播時，其傳播特性不僅會隨傳播距離變化，也受入射角度的影響。從角頻率成分來看，式(12)出現了角頻率為2ω的諧波分量，即為二次諧波。研究者常將二次諧波振幅與入射基波振幅的比值定義為非線性系數，從而進行研究[6]。因此，分別定義二次諧波沿x軸傳播分量的振幅A1x和沿y軸傳播分量的振幅A1y與入射基波的振幅A0之比的絕對值為非線性系數：

為研究二維非線性縱波在固體中傳播時產生的二次諧波的傳播特性，應用式(13)和式(14)，通過數值計算模擬非線性系數隨聲傳播距離和入射角的變化。其中材料參數選自文獻[22]，如表1所示。

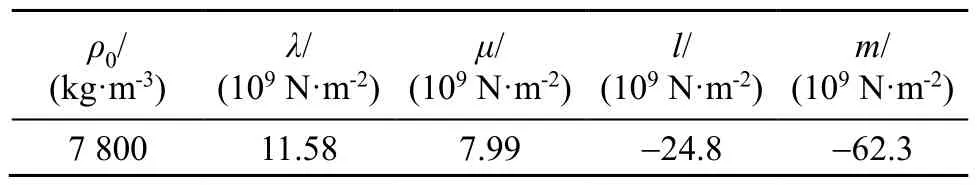
表1 某鋼軌樣品的二階和三階彈性常數Table 1 The second and third order elastic constants of a rail sample

圖 2為在入射波振幅為 1 μm，入射頻率為1 MHz時，不同入射角度下，非線性系數與聲傳播距離的關系圖。圖注中x表示二維縱波沿x軸傳播的位移分量，y表示二維縱波沿y軸傳播的位移分量。從圖2(a)中可以看出，隨著入射角的增大，非線性系數呈減小的趨勢。入射角為0°時，即垂直入射的情況，此時非線性效應最為明顯；入射角為 0°～30°時，非線性系數較大，說明此時非線性效應較為明顯；入射角為30°～60°時，非線性系數迅速減小；入射角大于 60°時，非線性系數趨于平穩，此時非線性效應較小；入射角為 90°時，即水平入射的情況，此時二次諧波沿y軸方向傳播，可認為沿x軸方向不存在非線性效應。

從圖 2(a)、2(b)中可以看出，隨著二維縱波在固體中傳播距離的增加，非線性系數和均逐漸增大，且隨著傳播距離的增加，非線性系數變化更明顯。這是由于聲波在固體中傳播時，會產生不同頻率的高次諧波，各階次諧波間會產生相互的影響，隨著聲傳播距離的增加，非線性效應積累增多，其非線性現象會更為明顯。

圖2 不同聲傳播距離的非線性系數|A1x/ A0|和|A1y/A0|與入射角關系圖Fig.2 Relationships of nonlinear parameters|A1x/ A0| and |A1y/A0|with incident angle at different sound propagation distances

為研究二維縱波在固體中傳播時，其入射振幅對非線性系數|A1x/A0|和 |A1y/A0|的影響，入射振幅A0依次取1、2、3、4、5 μm進行數值分析。

圖3為入射頻率為1 MHz時，不同入射角度下，非線性系數與入射振幅的關系圖。從圖3(a)和3(b)中可以看出，隨著入射振幅的增大，非線性系數逐漸增大，且入射角越小，非線性系數變化越明顯。這說明了振幅大的二維縱波在固體中傳播時，其聲擾動更強，聲波的非線性效應也更為顯著。

根據圖2中非線性系數與入射角的變化關系可知，選取入射角為 30°、45°和 60°的情況，可以很好地描述非線性系數的變化情況。從圖3(c)和3(d)中可以發現非線性系數與入射振幅呈正比例關系，且入射角越大，圖 3(c)中所對應的直線的斜率越大；圖3(d)中所對應的直線的斜率越小。

圖3 非線性系數|A 1x / A0|和 |A 1y/A0|與不同入射角及入射波振幅A0的關系圖Fig.3 Relationships of nonlinear parameters |A 1x/ A0| and |A 1y/A0|with incident angle and the amplitude A0 of incident wave

為研究二維縱波在固體中傳播時，其入射波頻率對非線性系數|A1x/A0|和|A1y/A0|的影響，入射波頻率取1、2、3、4、5 MHz進行數值分析。

圖4為入射振幅為1 μm時，不同入射角度下，非線性系數與入射頻率的關系圖。從圖4(a)和4(b)中可以看出，隨著入射頻率的增大，非線性系數逐漸增大，且入射角越小，非線性系數變化越明顯。這說明了入射縱波的頻率越大，其在波列中的質點單位時間內振動次數越多，即聲擾動更強。此時，二維縱波在固體中傳播所產生的非線性效應更為顯著。圖 4(c)和 4(d)選取了入射角 30°、45°和 60°的情況進行分析，可以發現非線性系數與入射頻率呈正相關，且入射角越大，圖4(c)中所對應的曲線遞增得越慢，即非線性效應越小；圖4(d)中所對應的曲線遞增得越快，即非線性效應越顯著。

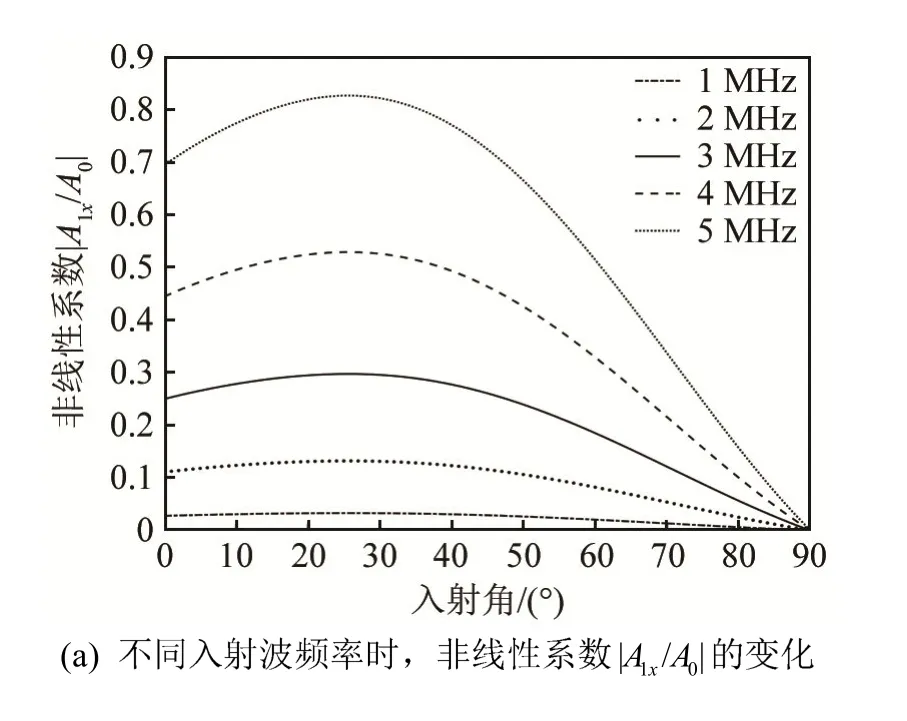
圖4 非線性系數|A 1x/A0|和|A 1y/A0|與不同入射角及入射波頻率f的關系圖Fig.4 Relationships of nonlinear parameters|A 1x/A0|and|A1y/A0|with incident angle and the frequency f of incident wave

3 結 論

本文從二維縱波非線性方程出發，圍繞聲馬赫數對該方程的解進行二階攝動展開，從而求解出二維縱波非線性方程的二階攝動解。根據計算結果定義了非線性系數|A1x/A0|和 |A1y/A0|(二次諧波沿 x軸傳播分量和沿y軸傳播分量與入射基波的振幅比)，并探究二維縱波在固體中傳播時其入射振幅、入射頻率、入射角以及聲傳播距離對非線性系數的影響。結果表明，非線性系數|A1x/A0|和|A1y/A0|與入射角有關，且垂直入射時非線性效應最為顯著；同時，二維縱波在固體中的聲傳播距離、入射振幅和入射頻率也是影響非線性系數|A1x/A0|和|A1y/A0|數值變化的因素。上述非線性系數可以用于描述二維縱波與二次諧波的傳播規律，并用于定性分析固體材料的非線性。為后續在固-固界面的研究基礎上進一步考慮固體材料的非線性的研究提供理論支持。

附錄Ⅰ