OPERATOR NORM AND LOWER BOUND OF FOUR-DIMENSIONAL GENERALIZED HAUSDORFF MATRICES*

Gholamreza TALEBI

Department of Mathematical sciences，Vali-e-Asr University of Rafsanjan，Rafsanjan，Islamic Republic of Iran E-mail:Gh.talebi@vru.ac.ir

Abstract The problem addressed is the exact determination of the operator norm and lower bound of four-dimensional generalized Hausdorffmatrices on the double sequence spaces Lp.A Hardy type formulae is found as an exact value for their operator norm and a Copson type formulae is established as a lower estimate for their lower bound.Further，exact values are found for the operator norm and lower bound of the transpose of generalized Hausdorffmatrices.

Key words four-dimensional Hausdorffmatrices

1 Introduction

For p＞0，let Lpdenotes the space of all double real or complex sequences x=such that‖x‖p:=＜∞，[3].Let V and W be two double sequence spaces and H=(hnmjk) be a four-dimensional in finite matrix of real or complex numbers.Then，we say that H defines a matrix mapping from V into W，and we denote it by writing H:V→W，if for every double sequence x=(xn，m)∈V，the double sequence Hx={(Hx)n，m}，the H-transform of x，is in W，where

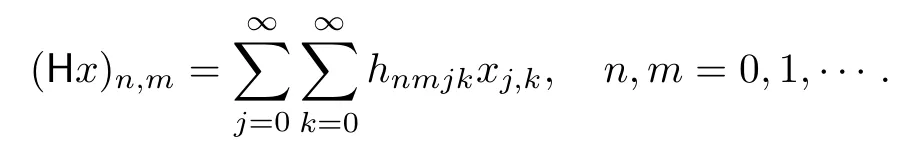
The operator norm and lower bound of a non-negative four-dimensional matrix H on the double sequence space Lp，are respectively defined by

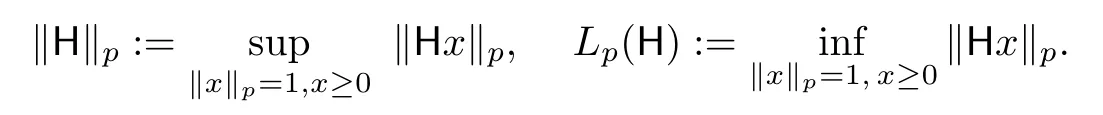
Obviously Lp(H)≤‖H‖p.To give full knowledge on the boundedness problem of four-dimensional matrices on double sequence spaces，we refer the readers to the recent papers[10-15]and to the monograph[2]for the four-dimensional triangle matrices，spaces of double sequences and related topics.

Let dμ and dλ be two Borel probability measures on[0，1].Then the four-dimensional generalized Hausdorffmatrixis defined by

Here a，b≥0，and the cases a=b=0 correspond to the ordinary four-dimensional Hausdorffmatrices[9].

In this paper，we are going to consider the boundedness problem of four-dimensional generalized Hausdorffmatrices and their transpose on the double sequence spaces.In our results，as we will see later，the two values

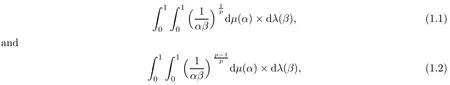
have essential roles.However，in the first integral for 0＜p＜1，and in the second integral for 1＜p＜∞，there are some singularity at the origin.For this reason，we have to restrict ourselves to those Borel probability measures dμ and dλ for which the above integrals exist.So，according to the subject under discussion，we may consider only the four-dimensional generalized Hausdorffmatrices associated with such measures.

2 Computation of the Operator Norm

In Theorem 3.1 of[10]，we found the exact value of.In the following，we extend it to the casewith a，b＞0.

Theorem 2.1Let 1＜p＜∞.Then the four-dimensional generalized Hausdorffmatrix is a bounded operator on Lpwith the operator norm

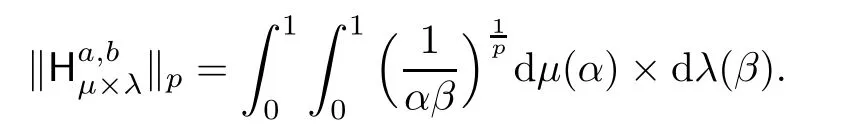
ProofLet x=(xn，m) be a non-negative double sequence in Lp.Clearly，we have

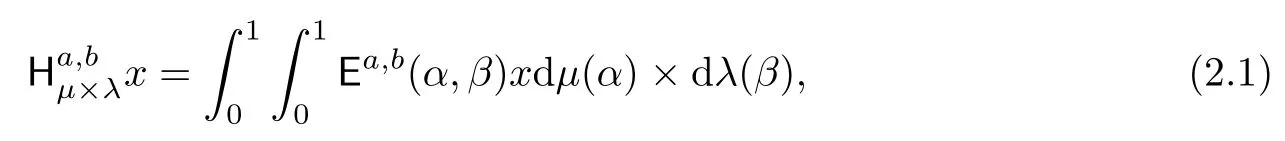
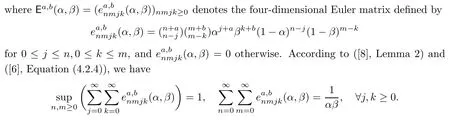
This implies by Theorem 3.3 of[14]，that

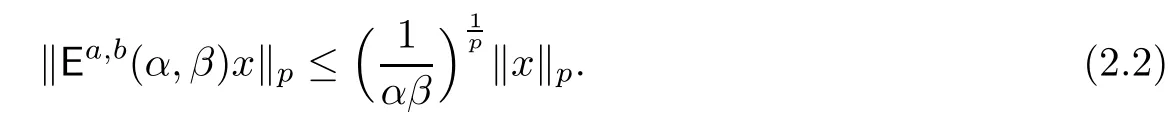
Applying Minkowski’s inequality together with (2.1) and (2.2)，we deduce that

Then we have x=(xn，m)∈Lp，and

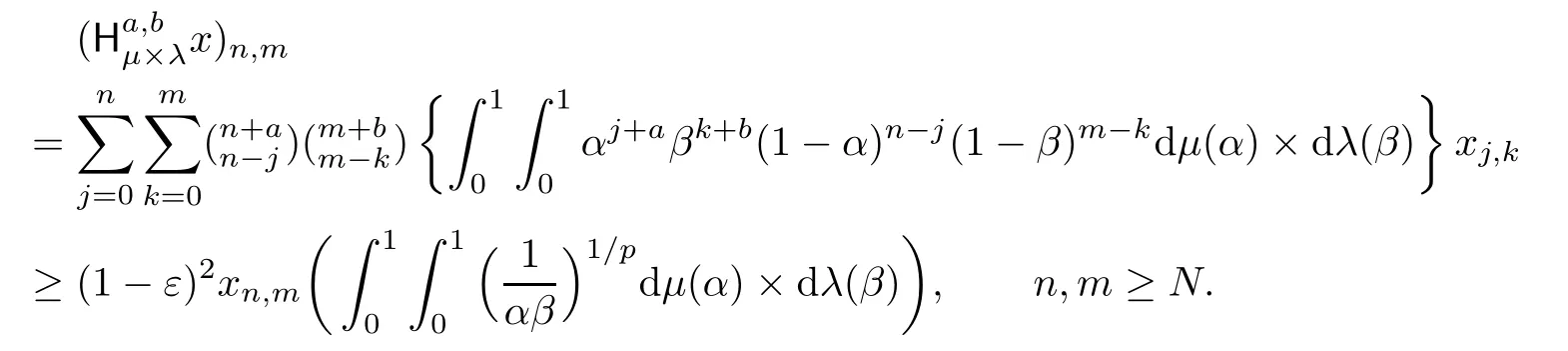
Since∈is arbitrary，this completes the proof. □

We remark here that Theorem 2.1 can be proved without the use of the Hardy’s method.It suffices to apply Theorem 2.2 of[13]to Corollary 1 of[1].

The generalized four-dimensional Euler and Cesàro matrices are the special cases of the generalized Hausdorffmatrices[14].Applying Theorems 2.1 to them，we have the following results.

Example 2.2Let 1＜p＜∞.Then the generalized four-dimensional Euler matrix Ea，b(α，β)，is a bounded operator on Lpwith the norm

Example 2.3Let 1＜p＜∞.Then the generalized four-dimensional Cesàro matrix Ca，b(α，β)，is a bounded operator on Lpwith the norm

For the operator norm of the transpose matrix，we have the following result as an extension of Theorem 4.1 in[13].Its proof is a consequence of Theorem 2.1.

Corollary 2.4Let 1＜p＜∞.Then the transpose of the generalized four-dimensional Hausdorffmatrix is a bounded operator on Lpwith the norm

Example 2.5Let 1＜p＜∞.Then the transpose of generalized four-dimensional Euler matrix is a bounded operator on Lpwith the norm

Example 2.6Let 1＜p＜∞.Then the transpose of generalized four-dimensional Cesàro matrix is a bounded operator on Lpwith the norm

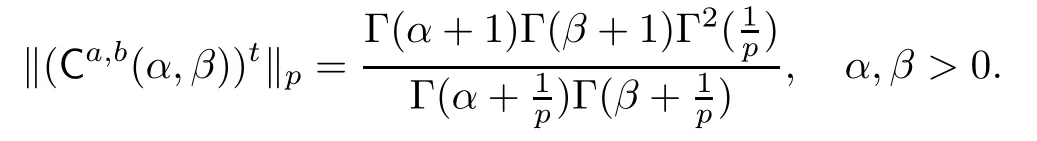
Remark 2.7For the case 0＜p≤1，the problem of finding the exact value ofis still open.

3 Computation of Lower Bound

For the ordinary four-dimensional Hasudorffmatrix，recently in Theorem 2.3 of[12]，we have found a suitable formulae for.In the following，we extend it to the casewith a，b＞0.

Theorem 3.1Let a，b＞0 and 0＜p≤1.Then

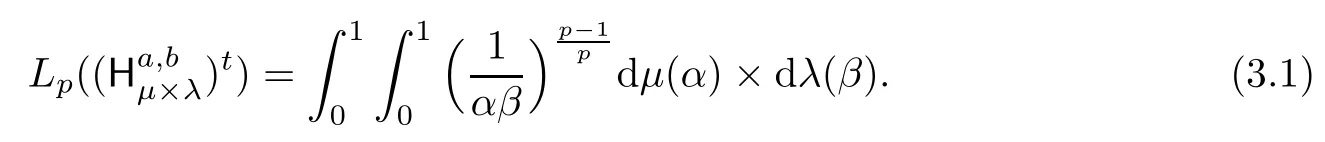
ProofFor a non-negative sequence x in Lp，we can easily obtain

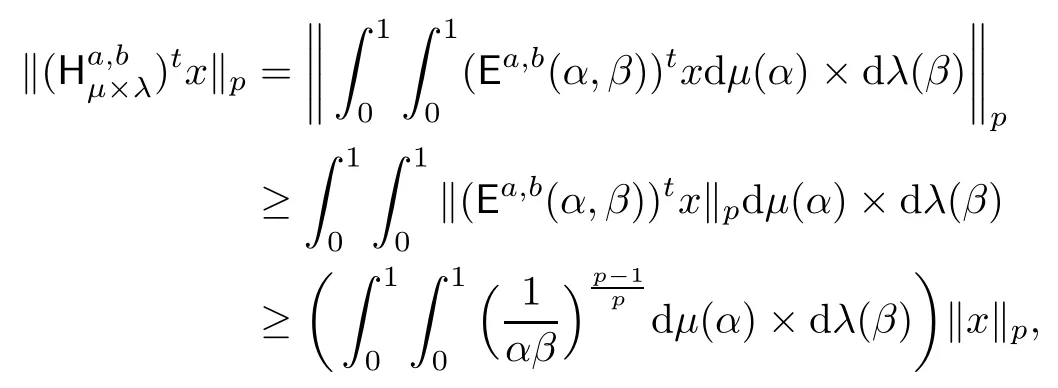
which implies

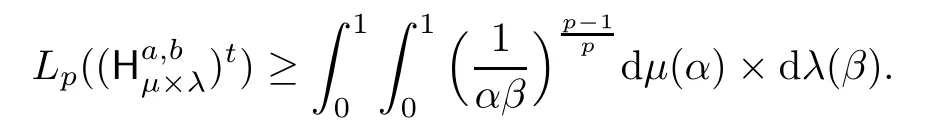
To show that the constant in (3.1) is the best，inspired by Bennett’s proof ([4]，p.33)，suppose that ρ＞1/p and that n0，m0are fixed integers with n0，m0≥ρ.Consider the double sequence (zj，k)=，where

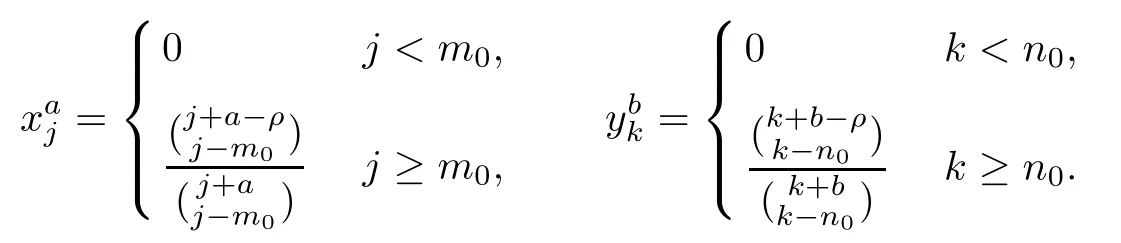
Then z=(zj，k)∈Lp，and we have

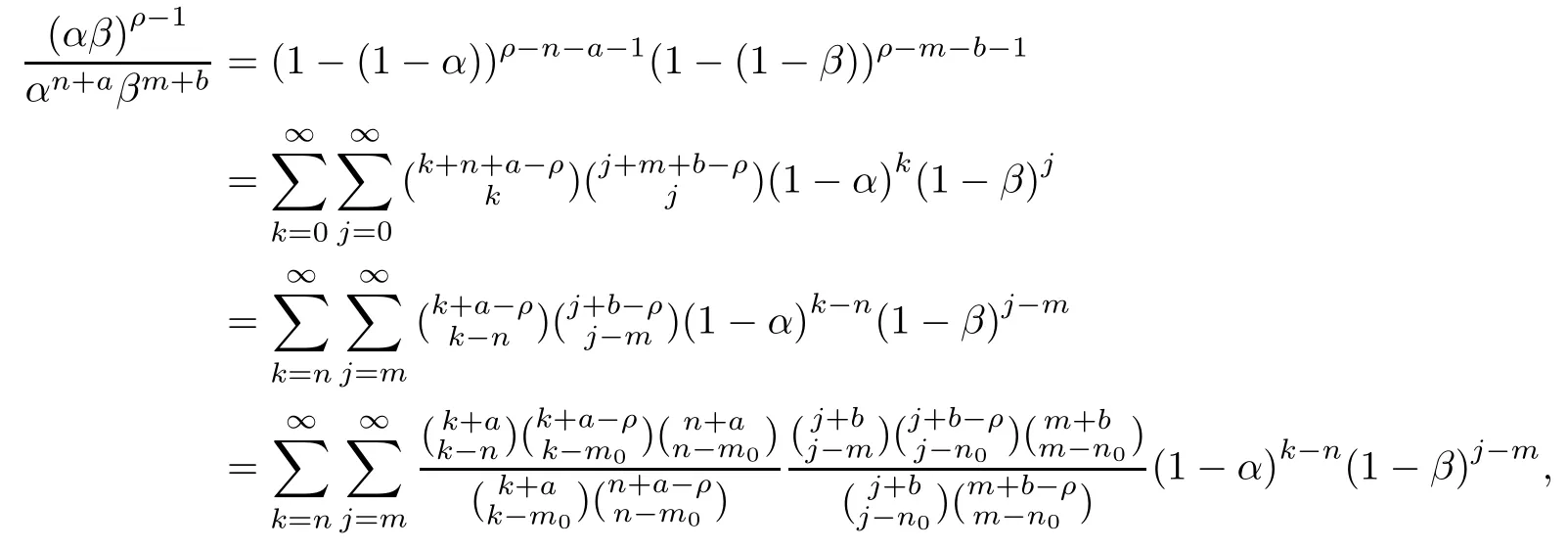
which implies that

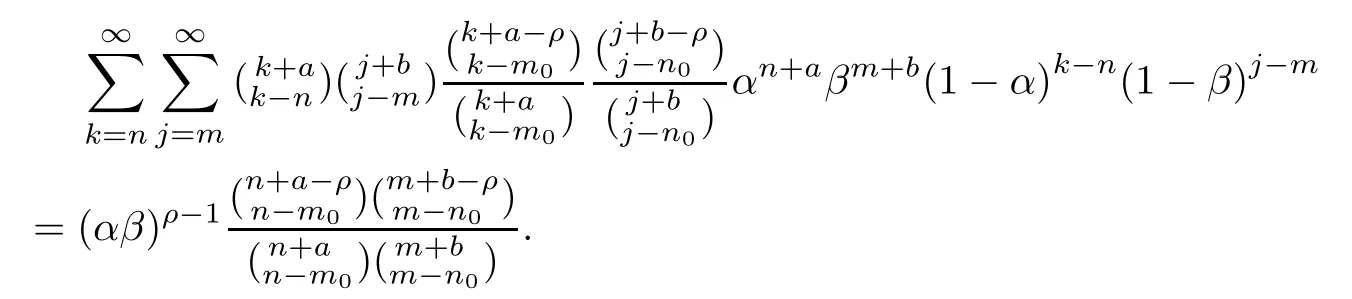
By integrating against dμ(α)×dλ(β)，we get

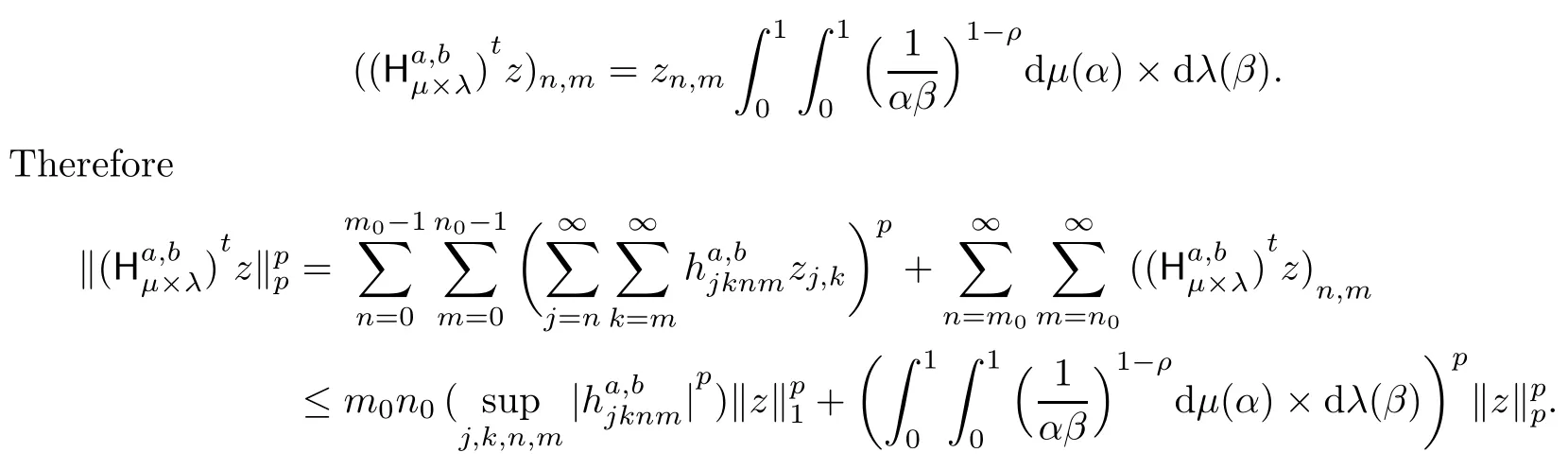
Now if ρ→1/p，then‖z‖p→∞，which gives us

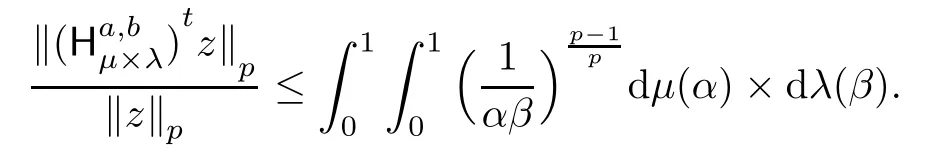
This shows that the constant in (3.1) is optimal and completes the proof. □

Example 3.2Let a，b＞0 and 0＜p≤1.Then for all α，β∈(0，1)，we have

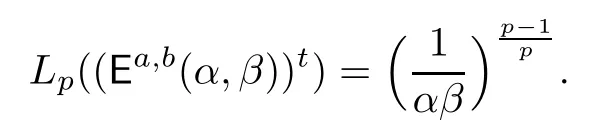
Example 3.3Let a，b＞0 and 0＜p≤1.Then for all α，β＞0，we have

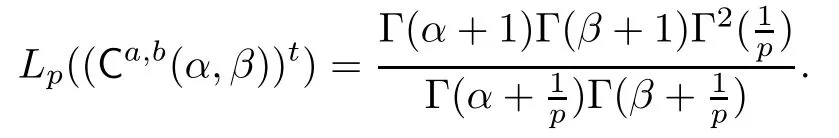
We observe that the inequality

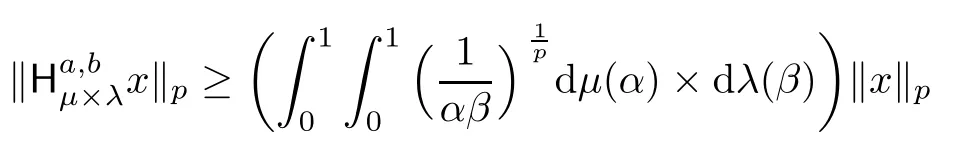
can be obtained in a similar way as in the proof of the proceeding theorem，and enables us to obtain the following generalization of Theorem 2.7 in[12].

Theorem 3.4Let a，b≥0，0＜p≤1.Then

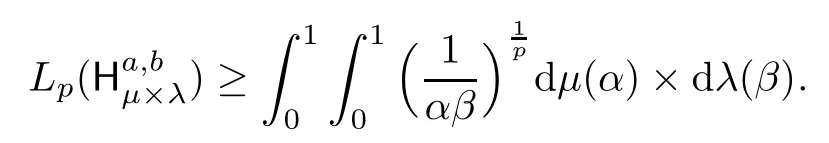
Example 3.5Let 0＜p≤1 and α，β∈(0，1).Then

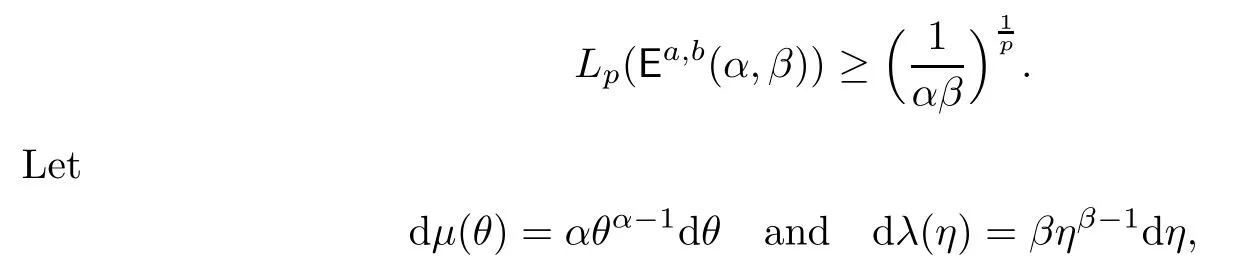
where α，β＞0.Then the associated generalized four-dimensional Hausdorffmatrix is called the generalized four-dimensional Gamma matrix Γa，b(α，β)，for which we have the following results.

Example 3.6Let a，b＞0 and 0＜p≤1.Then

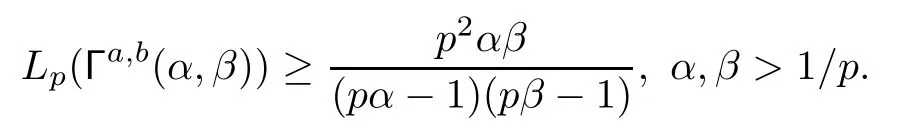
Example 3.7Let 1＜p＜∞.Then the generalized four-dimensional Gamma matrix is a bounded operator on Lpwith the norm

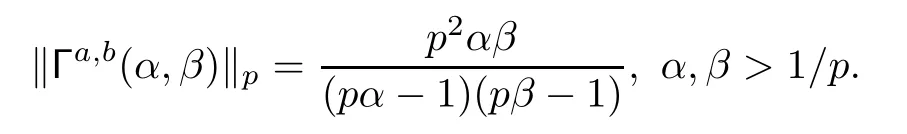
We note that if α or β is less than or equal to，the singularity of the integral (1.1) at the origin is non-integrable.So，in both Examples 3.6 and 3.7，we only consider the cases α，β＞1/p.

Example 3.8Let a，b＞0 and 0＜p≤1.Then

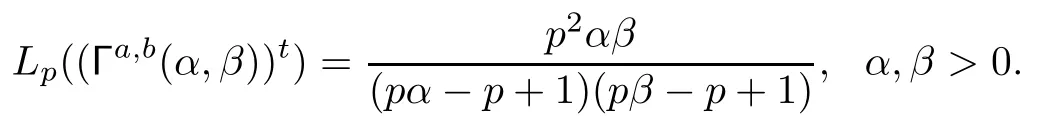
Example 3.9Let 1＜p＜∞.Then the transpose of the generalized four-dimensional Gamma matrix is a bounded operator on Lpwith the norm

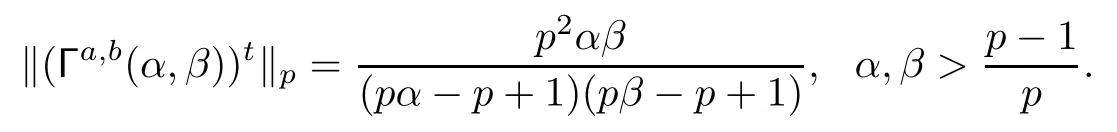
Again we note that if α or β is less than or equal to (p-1)/p，then the singularity of (1.2) at the origin is non-integrable.Therefore，in Example 3.9，we only consider the cases α，β＞(p-1)/p.

Remark 3.10For the four-dimensional Cesàro matrix C0，0(1，1)，since the singularity of (1.1) is non-integrable for 0＜p≤1，the estimate in Theorem 3.4 gives us somewhat strange.The constant in this estimate is in finite and writing the below estimate with in finite constant seems to be formally incorrect.

Remark 3.11For the case 1＜p＜∞，recently in Theorem 4.3 of[13]，we have obtaind the following results for The lower bound of the ordinary four-dimensional Hasudorffmatrix and its transpose，respectively;

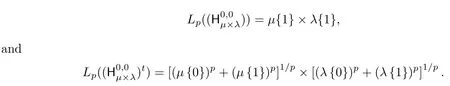
For the four-dimensional generalized Hausdorffmatrix and its transpose，using Theorem 6.1(ii) and Theorem 6.2(iii) of[5]together with Theorem 2.1 of[13]，we have the following results，respectively;

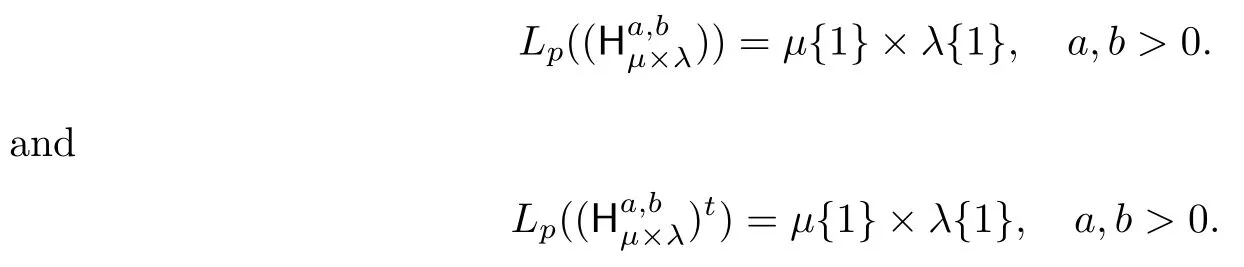
AcknowledgementsWe would like to thank Professor Graham Jameson and Professor Billy E.Rhoades for their technical assistance during the preparation of the present paper.