考慮成批供料的大規模下料問題

郝信燁 劉懋圻 張燦榮 鄭力

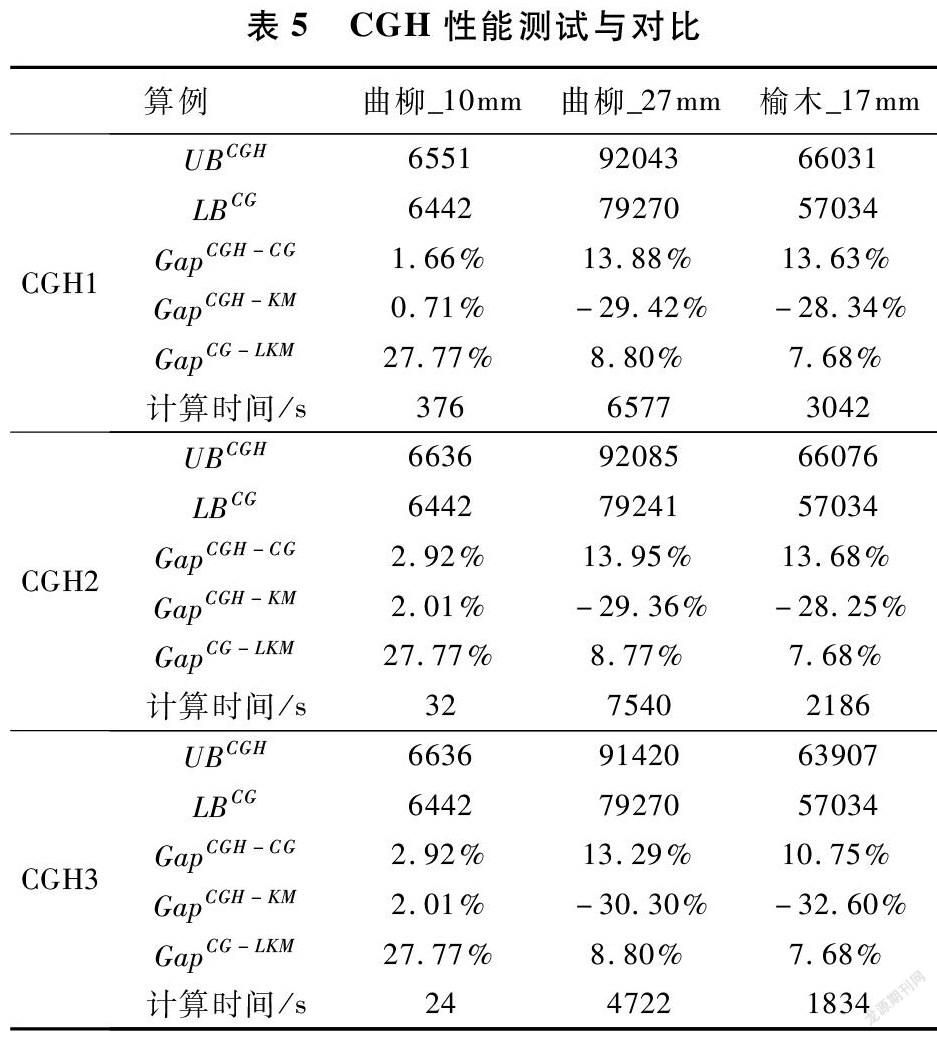
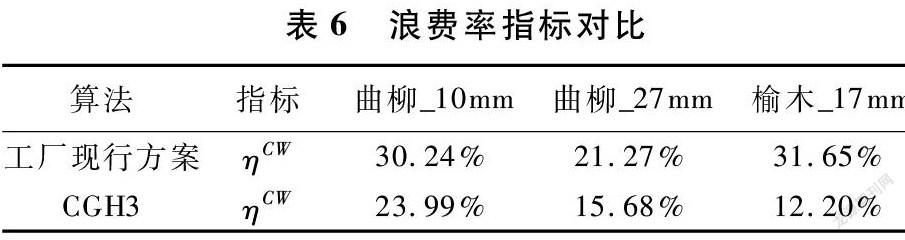
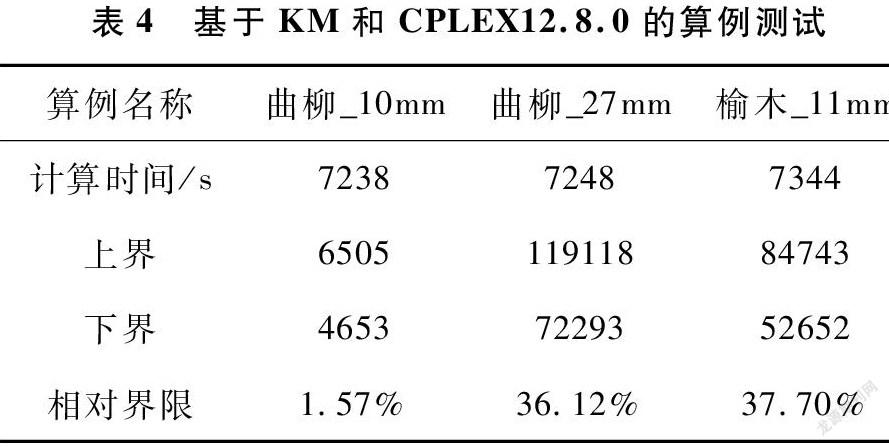
摘 要：本文基于某家具廠實際生產場景，在大規模下料問題中考慮了成批供料等現實生產因素。我們建立了Kantorovich模型，其對應的算例具有規模大、解空間對稱等特點，難以直接求解。為了解決計算困難，基于Dantzig-Wolfe框架將其分解，并通過列生成求解線性松弛主問題得到較緊的下界。通過對子問題的結構分析，將其分解為可獨立求解的二級子問題。基于歸并且還原設計了三種子問題求解方式，有效縮減了子問題求解規模，并克服了解空間對稱性，進而加速列生成迭代。基于工廠實際數據進行數值實驗，結果表明：本列生成啟發式算法優于商用求解器CPLEX，其在較短計算時間內得到高質量的解。相比于工廠現行算法，本算法降低10.43%的下料浪費。

關鍵詞：板材下料;成批供料;大規模混合整數規劃;列生成;歸并且還原

中圖分類號：TB114.1 文獻標識碼：A 文章編號：2097-0145（2022）01-0009-08 doi：10.11847/fj.41.1.9

Abstract：This paper stems from a real production research. It studies a large-scale cutting stock problem considering batch feed and some other constraints based on the real production. We establish a Kantorovich model， the instances corresponding to which are hard to solve due to the large scale and symmetry in the solution space. To tackle the computational difficulty， we decompose it based on the Dantzig-Wolfe framework， and solve the linearly-relaxed master problem by column generation in order to generate tight lower bounds. Based on the analysis of the structure， we decompose the sub-problems into second-level sub-problems which can be solved independently. Based on the idea of merge and recover， we develop three methods to solve the sub-problems， which reduce the scale of sub-problems and overcome the symmetry in the solution space， leading to accelerating the column generation process. We conduct computational experiments based on the real data from the factory. The experimental results indicate that， our approach outperforms CPLEX， a commercial solver. It can generate high-quality solutions in short computation time. Compared with the algorithm presently used in the factory， our approach reduces the cutting waste by 10.43%.

Key words：cutting stock; batch feed; large-scale mixed integer programming; column generation; merge and recover

1 引言

下料問題（Cutting Stock Problem，CSP）是眾多行業中（如造紙業[1]、造船業[2]）面對的一個重要問題，其以最小化成本為目標，通過對庫存板材的切割，來滿足不同尺寸類型的需求[3～5]。合理的下料方案會為實際生產減少浪費，帶來經濟效益。基于同某家具廠合作的實際生產項目，本文對該廠CSP進行研究。該廠拼合板產品生產過程如下，盛有不同規格板材的托盤被挑選并從倉庫中運到線上，工人將刀具預設為若干種標準寬度，并在板材寬度方向上進行水平切割（順沖工序），產生短條;之后，在垂直方向上切去影響美觀的木料疤痕（橫截工序），產生橫截小塊，并將橫截小塊指接成長條;最終，用從長條上切下的拼合塊進行產品拼合。……