毛竹管樁基坑支護可靠性研究

鄧友生，付云博，葉建軍，彭程譜，李令濤

(1.西安科技大學 樁承結構研究中心，陜西 西安 710054；2.湖北工業大學 土木建筑與環境學院，湖北 武漢 430068)

0 引 言

支護樁以良好的抵抗變形能力廣泛用于基坑建設中，完善的技術與高適應性保證工程支護的穩定性[1-2]。傳統混凝土樁用于支護有施工周期長、成本較大等缺點，倘若不滿足工程需要，容易產生工程事故[3-4]。尤在土質條件復雜時，基坑事故發生頻率最高，支護樁使用功能直接影響基坑穩定性[5]。

可靠度是評價支護樁使用功能的重要指標[6]。樁基工程中對可靠度的研究已取得了一些成果，JIANG等采用響應面法對傾斜場地橫向受荷樁可靠度分析樁頂位移變異性與荷載的關系[7]。MANISH等以最小二乘法和高斯回歸建立群樁支護可靠度指標公式對比一次二階矩法，新方法有更強的適應性[8]。邊曉亞等以樁基長徑比、容許沉降和沉降控制條件為影響因素，利用均值一次二階矩法計算群樁可靠度指標[9]。陳飛等針對離子型稀土礦山滑坡問題，以竹樁為主進行生態護坡，有效提高了邊坡穩定性[10]。基于Copula理論，唐小松等考慮參數不確定性提出基樁荷載—位移雙曲線概率分布方法[11]；辛軍霞等針對土體參數離散型過大問題，改進了CFG樁復合地基的可靠性評估[12]。鄧友生等使用竹樁對基坑進行支護試驗，利用有限差分法對比分析，基坑支護中使用毛竹管樁具有較好效果，表明環保支護體系的可行性[13-14]。戴自航等針對毛竹復合土釘墻支護變形預測與控制方面，建立有限元模型，分析認為竹樁長度對坡體水平位移影響較明顯[15]。JANUSZ等采用近似響應面法建立加載樁極限狀態函數，對嵌入垂直裂縫的非飽和基底單樁進行可靠性評價，結果與飽和度最相關[16]。郝騰結合JC法與一般分離法研究螺旋樁復合地基可靠度，結果表明樁端阻力變異系數和地基承載力折減系數對可靠指標影響較大[17]。JIANG等考慮土體參數的分布狀態，分析各參數對邊坡可靠指標的影響[18]。

目前多以極限狀態下最大荷載為失效準則，對承載樁進行可靠性評估。但在樁基受荷未達到極限承載力卻已經不滿足工程安全性需求時，計算的可靠度指標無法體現正常使用狀態下支護樁使用功能，導致工程事故頻發。毛竹管樁具有較好的承載能力，屬綠色建材，可有效降低能耗，綠色無污染符合可持續發展戰略，對毛竹管樁應用于基坑支護進行可靠性分析，為推進工程化提供理論基礎。針對此問題，引入中心點法分別以樁頂容許位移、計算位移和極限與容許位移比為基本影響因素，分析毛竹管支護樁正常使用極限狀態和承載能力極限狀態下各參數對可靠度指標的影響規律。

1 模型因子及變量

不確定因素對不同組樁頂位移數據的影響使無法直接進行可靠性對比，同種因素下難以收集足夠的數量進行統計，為增大樣本容量，消除不同組樁頂位移差異性，引入竹樁樁頂位移試計比λ

(1)

式中dm和dp分別為支護樁樁頂實測位移和計算位移。

防止基坑變形失控狀態發生，應在支護承載接近極限變形處設置警戒值。變形觸動警戒值應及時補強支護體系。警戒值設定應接近極限變形，并保證在基坑發生失穩前留足夠的反應時間[19]。受土質條件、施工方法等因素的影響，差異性無法定量分析，故設樁頂位移容許值為警戒值，表示為dtol，采用極限狀態方程建立功能函數Z

Z(dm)=dtol-dm

(2)

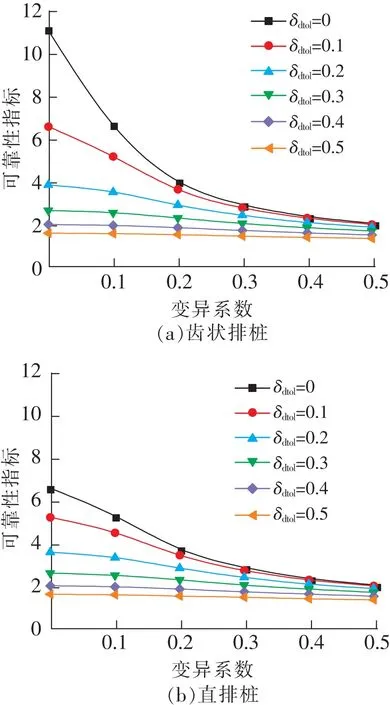
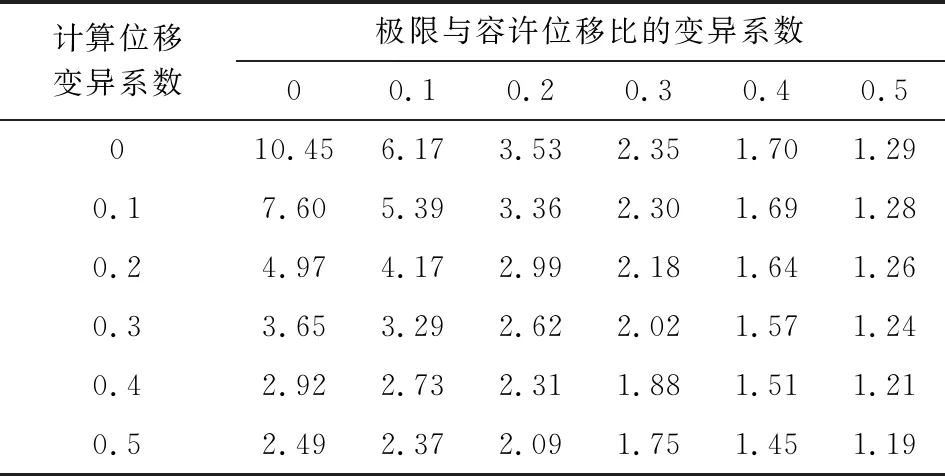
當Z=0時，表示竹樁支護能力在臨界狀態；當Z<0，即dtol

P=Pr(dtol

(3)

支護樁可靠度設計常引用安全系數K，定義為容許位移與計算位移的比值

(4)

式中μdtol為容許位移平均值；μdp為計算位移的平均值。

文獻[20]中樁基理論分析時，安全系數K取3.5，試驗設計時，K取值2.0。竹樁為天然毛竹制作而成，強度較混凝土略顯不足。設安全系數取2.0，2.5，3.0，3.5，利用中心點法分別計算得可靠性指標為2.16，3.00，3.69，4.28。當可靠度在2.5～3.5之間時，安全級別屬于中等。因此，為滿足正常使用極限狀態與承載能力極限狀態下可靠性及經濟性要求，安全系數取2.5。

在對支護樁進行可靠度分析時，應檢驗相關變量的分布特性，樁頂位移是重要的基本統計參數。程志和進行了分步開挖、加載過程下直排與齒狀毛竹管樁對基坑支護作用的足尺模型試驗[21]，支護結構體系如圖1所示。利用上述計算方法和收集的實測數據，計算支護樁的位移和試計比(表1)。

圖1 基坑支護結構體系

表1 樁頂位移偏差統計

在同為黏性土、毛竹管樁和靜壓加載條件下，2種布樁方式的λ差別不大，但λ的變異系數有較大差異，兩者相差0.06，齒狀排樁λ的變異系數較小，是直排樁支護體系的46%。試驗中直排樁樁頂前緣出現略微土塊脫落，齒狀排樁支護下基坑側壁未出現明顯變形，樁頂位移整體小于直排樁。表明齒狀排樁較直排樁能更好地支護基坑變形，減小樁頂位移的變異性。

采用Kolmogorov-Smirnov(簡稱K-S)檢驗法和Anderson-Darling(簡稱A-D)檢驗法，顯著性水平取0.05，分析在正態分布、對數正態分布和極值Ⅰ型分布下，樁頂位移偏差統計量的統計特性。由K-S檢驗和A-D檢驗結果(表2)得到試計比的統計值均小于臨界值，表明2種檢驗法對假定的3種分布均接受。對數正態分布統計值為0.15和0.23，3種分布中為最小值，樣本更收斂。

表2 試計比統計檢驗結果

2 正常使用極限狀態

根據中心點法，依據對數正態分布對基本變量進行設計計算，可靠度指標β

(5)

式中μZ為功能函數Z的均值；σZ為功能函數Z標準差。

BIAN等對受荷樁兩種極限狀態下的可靠指標進行了線性分析[22]。借鑒此線性關系，在正常使用狀態下，λ，dtol和dm服從對數正態分布。結合中心點法，竹樁支護失效概率及可靠度指標βsls

pfs=P(dtol

(6)

為考慮成樁方式在支護樁可靠度分析中的影響，以計算位移變異系數(δdp)與容許位移變異系數(δdtol)為基本變量，取值范圍0～0.5，對毛竹管支護樁進行可靠度計算。由圖2(a)，βsls隨著δdp從0遞增到0.5呈現明顯的下降趨勢，曲線則表現得愈加平緩，表明βsls值隨δdp的增大而減小，即計算位移變異系數的增大使得支護樁可靠性降低，但影響幅度逐漸減弱；δdtol從0至0.5所對應圖2(a)中的6條曲線整體依次降低，δdtol為0時βsls曲線整體最大且最為陡峭，最大值為11.07，最小值為1.46，陡峭程度隨δdtol的增大而降低，表明dtol的不確定性愈大，支護樁的可靠性越低。

依據小概率事件，失效概率5%，可靠指標大于1.65，判定支護能力滿足安全要求[23]。圖2(a)中，當δdtol=0.5時全部不符合安全要求，δdtol=0則全部滿足。δdtol=0.4時，δdp=0.2的可靠指標βsls為1.72雖然滿足要求，但其僅高于判別值0.07，風險較大。因此對支護樁進行可靠性分析時，相較于計算位移更要充分考慮容許位移的不確定性。

圖2 正常使用極限狀態下變異系數與可靠性指標關系

齒狀排樁與直排樁支護下βsls的變化情況類似，表明齒狀與直排兩種布樁方式在δdp與δdtol影響因素下支護樁可靠性趨勢并無明顯區別。兩種布樁方式下βsls的差值較小，且齒狀排樁支護下βsls略大。但在忽略計算位移與容許位移的影響時，即δdp與δdtol都為0，直排樁支護下βsls=6.54，是齒狀布樁方式下的60%。

齒狀布樁方式提高了可靠度評價結果。其原因在于齒狀排樁支護設計對樁頂位移有一定的抑制作用，對基坑的支護更加穩定，致使λ的變異系數較低，有效減少了樁頂位移試計比的變異性，提高了可靠性。

3 承載能力極限狀態

以樁頂容許位移與計算位移為基本變量的可靠度計算方程，屬正常使用極限狀態下穩定性設計。實際樁頂位移觸及警戒值時，整體支護結構未失效但未達到預期效果，在進行補強加固同時，相對于βsls，更需可靠度設計計算此極限狀態下的指標βuls。

支護體系穩定性分析中，極限狀態下的容許位移并不能完整映像基坑支護可靠度。依據不穩定因素影響，引入極限位移與容許位移的無量綱試計比(λu)，較傳統承載能力極限狀態可靠度設計，具有更高安全性、準確性。以下可靠指標設計時取λu作為主要變量，分析極限與容許位移比均值μλu及其變異系數δλu(0～0.5)、δdp(0～0.5)與βuls的關系。將收集的兩組試驗數據綜合處理，正常使用極限狀態試計比均值μλ為1.095，變異系數δλ為0.11(表3)。

表3 極限與容許位移比的變異系數對可靠性指標的計算結果

δλu和δdp以相同值變化，δλu隨βuls呈變化增大趨勢，因此δλu對βuls的影響高于δdp，變化率隨變異系數遞變而增大：將δλu=0,δdp=0，βuls=10.45設為定值組，當δλu和δdp分別取值0.5時，極限與容許位移比的βuls結果為1.29，計算位移變異系數的βuls為2.49，較定值組，二者的可靠指標變化值相差1.20。承載能力極限狀態下的可靠性設計中，極限位移與容許位移比的判定尤為關鍵。

隨著δλu和δdp遞變，βuls變化趨勢在0.2處轉變。變量小于0.2時，βuls值隨變異系數的增大而加速減少，曲線較大于0.2時更加陡峭。表明可靠性指標隨變量的增加呈先加速下降，經0.2后下降衰減趨勢。變量δλu和δdp對可靠度指標影響整體趨勢呈持續減弱。

考慮λu的變化，在研究極限承載能力對竹樁支護能力可靠度指標的作用時，將其分為三類討論(μλu取1.1，1.3，1.5)，分別計算可靠度指標，以探討在承載能力極限狀態下對支護竹樁可靠度指標的作用。

比較圖3不同極限與容許位移比下可靠性指標，隨著μλu的增大βuls逐漸增大。當δdp和δλu不斷增加時，不同極限位移與容許位移比的均值之間βuls差值開始縮小，且βuls的減少速率快于μλu增大速率。表明δdp對βuls的影響較為顯著，且影響程度大于μλu。因此，有效抑制干擾設計位移，降低變異性是提高支護體系可靠性的主要因素。

圖3 承載能力極限狀態下變異系數與可靠性指標關系

以安全級別不低于中等，即βuls≥2.5為目標可靠度[24-25]。當δλu=0.3時，μλu=1.1條件下的βuls全部不滿足目標可靠度，而μλu=1.5時，δdp=0.1下βuls=2.63滿足目標可靠度。在設計時先確定目標可靠度，然后根據現場土質情況等來設計并計算出極限與容許位移比。而土質參數和施工條件往往具有較大誤差，難以精確控制，此時需要提高極限預估量，即增大極限位移與容許位移比來滿足工程穩定性。

4 結 論

1)毛竹管樁樁頂位移承載能力極限狀態可靠度指標可由正常使用極限狀態可靠度指標線性表達。

2)樁頂容許位移與計算位移的變異系數對支護樁βuls呈負相關，在低變異性下影響較為顯著，轉折點為0.2；對支護樁進行可靠性分析時，相較于計算位移更要充分考慮容許位移的不確定性。

3)在正常使用極限狀態下，齒狀排樁較直排樁有更優的可靠度，隨著樁頂計算位移與容許位移的變異性增加，二者可靠度指標差異性逐漸減小。

4)毛竹管樁βuls隨μλu不確定性的增大而減少，隨μλu的增加而變大。樁頂設計位移定量時，為滿足目標可靠度，可適當提高極限位移與容許位移比或降低其變異性來滿足需要。