詳談導數處理函數性質難點問題
亢愛鋒
(山東省青島第九中學)
利用導數研究函數單調性是高考數學的重點、熱點和難點.因為導數涉及的知識能力和思維層次要求較高,學生運用好導數這個“工具”,對提升學生的分析問題、解決問題、邏輯思維等綜合能力都有很大的幫助.其中,利用導數討論函數單調性的核心是在定義域內判斷導函數的正負.而判斷導函數的正負,綜合考查學生觀察分析和綜合運用函數、不等式、零點等知識,配方、分離變量和因式分解等數學方法,考查學生對函數與方程、數形結合、等價轉化等數學思想掌握情況.高考在這一部分的考查可謂是“芝麻開花節節高”.根據多年對高考題的研究和教學的反思總結,筆者將積累下來的如下解題方法分享給讀者.
例1(2015 年全國Ⅱ卷理21,節選)設函數f(x)=emx+x2-mx.證明:f(x)在(-∞,0)單調遞減,在(0,+∞)單調遞增.

易知f′(x)=m(emx-1)+2x.
當x<0時,2x<0.
若m>0,則emx<1,emx-1<0,m(emx-1)<0,故f′(x)<0,因此f(x)在(-∞,0)上單調遞減.
若m<0,則emx>1,emx-1>0,m(emx-1)<0,從而f′(x)<0,因此f(x)在(-∞,0)上單調遞減.
故當x<0 時,函數f(x)在(-∞,0)上單調遞減.
當x>0時,2x>0.
若m>0,則emx>1,emx-1>0,m(emx-1)>0,故f′(x)>0,因此f(x)在(0,+∞)上單調遞增.
若m<0,則emx<1,emx-1<0,m(emx-1)>0,故f′(x)>0,因此f(x)在(0,+∞)上單調遞增.
故當x>0時,f(x)在(0,+∞)上單調遞增.
綜上,f(x)在(-∞,0)上單調遞增,在(0,+∞)上單調遞增.
例2求函數f(x)=-x+1的單調區間.

f′(x)=(x>0),因此判斷函數單調性的關鍵是判斷g(x)=1-lnx-x2(x>0)的正負,有以下幾種解法.
方法1圖像法
觀察可知g(x)是由基本初等函數構成的,所以可以將g(x)的正負轉化為函數g(x)的零點問題.
令g(x)=0,移項得1-x2=lnx,作出函數y=1-x2,y=lnx的圖像,如圖1所示.

圖1
由圖1可知,當0<x<1時,1-x2>lnx,所以f′(x)>0,故f(x)在(0,1)上單調遞增;當x>1時,1-x2<lnx,所以f′(x)<0,故f(x)在(1,+∞)上單調遞減.
方法2分組正負判斷法
因為1-x2,lnx的正負均取決于x與1的大小關系,所以將定義域分為0<x<1,x>1兩種情況分類討論1-x2,lnx的正負.
當0<x<1時,1-x2>0,lnx<0,所以1-x2-lnx>0,g(x)=1-lnx-x2>0,f′(x)>0,故f(x)在(0,1)上單調遞增.
當x>1 時,1-x2<0,lnx>0,所以1-x2-lnx<0,g(x)<0,f′(x)<0,故f(x)在(1,+∞)上單調遞減.
方法3二次求導法
構造決定導函數f′(x)正負的核心函數g(x)=1-lnx-x2(x>0),則g′(x)=--2x,顯然g′(x)<0恒成立,故g(x)在(0,+∞)上單調遞減.又g(1)=0,所以g(x)在(0,+∞)內有唯一零點為x=1.故當0<x<1時,g(x)>0;當x>1時,g(x)<0.因此,當0<x<1時,f′(x)>0;當x>1時,f′(x)<0,于是f(x)在區間(0,1)上單調遞增,在(1,+∞)上單調遞減.
例3已知f(x)=x-lnx,g(x)=當x∈(0,e]時,比較f(x),g(x)的大小.

比較f(x),g(x)的大小,即判斷f(x)-g(x)在x∈(0,e]的正負.令

例4證明:當x>0時,x2<ex.

即證f(x)=x2-ex<0在x>0時恒成立.f′(x)=2x-ex,g(x)=2x-ex(x>0),則g′(x)=2-ex,易知當0<x<ln2 時,g′(x)>0,g(x)單調遞增;當x>ln2時,g′(x)<0,g(x)單調遞減,所以gmax(x)=g(ln2)=2ln2-2<0,所以f′(x)<0恒成立,故f(x)在(0,+∞)上單調遞減,因此f(x)<f(0)=-1,顯然f(x)=x2-ex<0,從而x2<ex.
例5已知函數f(x)=(x>0).
(1)求函數f(x)在(0,+∞)上的單調性;
(2)當x>0時,f(x)>恒成立,求整數k的最大值.


因為x>0,所以x2>0,>0,ln(x+1)>0,則f′(x)<0,所以f(x)在(0,+∞)上單調遞減.
(2)方法1由已知得,當x=1 時,k<2(1+ln2)<4,因為k∈Z,故kmax=3,因此只需證當k=3時,f(x)>(x>0)恒成立,即證(x+1)ln(x+1)+1-2x>0(x>0)恒成立.
令g(x)=(x+1)ln(x+1)+1-2x(x>0),則g′(x)=ln(x+1)-1.當x>e-1 時,g′(x)>0,g(x)單調遞增;當0<x<e-1時,g′(x)<0,g(x)單調遞減,從而gmin(x)=g(e-1)=3-e>0,證畢.
方法2即證h(x)=k(x>0)恒成立,即hmin(x)>k.對h(x)求導得
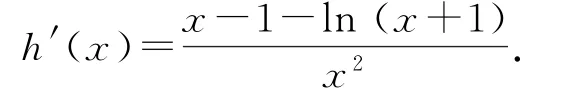
令φ(x)=x-1-ln(x+1)(x>0),則φ′(x)=>0,所以φ(x)在(0,+∞)上單調遞增.又φ(2)=1-ln3<0,φ(3)=2-2ln2>0,所以φ(x)=0有唯一實根,設為a,則a∈(2,3),a=1+lna+1.
根據單調性可知,當x>a時,φ(x)>0,h′(x)>0,h(x)單調遞增.當0<x<a時,φ(x)<0,h′(x)<0,h(x)單調遞減,從而hmin(x)=h(a)==a+1∈(3,4),因此正整數k的最大值為3.
例6已知函數f(x)=(k為常數,e=2.71828…是自然對數的底數),曲線y=f(x)在點(1,f(1))處的切線與x軸平行.
(1)求k的值;
(2)求f(x)的單調區間.


(2)由(1)可知f′(x)=.設g(x)=-lnx-1,則g′(x)=-<0,即g(x)在(0,+∞)上單調遞減.由g(1)=0 知,當0<x<1時,g(x)>0,從而f′(x)>0,當x>1時,g(x)<0,從而f′(x)<0.
綜上,f(x)的單調遞增區間是(0,1),單調遞減區間是(1,+∞).
通過以上例題可以看出,導數法研究函數性質的難點在于如何確定導數的正負,所以解決了導數正負的問題,也就解決了導數的根本.無論是高考題還是平時的模擬訓練,通過圖像法、逐項或分組判正負法、二次求導(三種不同解決渠道)這三種方法的不斷練習,均可以提高學生的邏輯思維能力.
(完)

