線(xiàn)性Boussinesq方程的色散量子化現(xiàn)象

張苗苗, 李茂華

線(xiàn)性Boussinesq方程的色散量子化現(xiàn)象

張苗苗, 李茂華*

（寧波大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 浙江 寧波 315211）

為研究線(xiàn)性Boussinesq方程的周期初邊值問(wèn)題解在大波數(shù)條件下的漸近行為, 通過(guò)將方程解表示成Fourier級(jí)數(shù)形式, 利用Matlab軟件進(jìn)行數(shù)值模擬. 結(jié)果表明: 方程色散關(guān)系的漸近行為對(duì)方程解在大波數(shù)條件下的漸近行為起決定性作用, 線(xiàn)性Boussinesq方程存在色散量子化現(xiàn)象.

線(xiàn)性Boussinesq方程; 周期初邊值問(wèn)題; 色散關(guān)系; 漸近行為; 色散量子化

20世紀(jì)90年代, Berry[1]在研究周期域上線(xiàn)性Schr?dinger方程時(shí)發(fā)現(xiàn)其解有明顯的動(dòng)力學(xué)行為, 進(jìn)一步研究得到: 初值條件為階梯函數(shù)的解在有理時(shí)刻為分段函數(shù); 在無(wú)理時(shí)刻呈現(xiàn)類(lèi)分形連續(xù)不可微狀態(tài). Talbot[2]發(fā)現(xiàn)這一現(xiàn)象在光學(xué)實(shí)驗(yàn)中也存在. 因此, Berry稱(chēng)這一現(xiàn)象為T(mén)albot效應(yīng). 緊接著B(niǎo)erry等[3-4]發(fā)現(xiàn)這種現(xiàn)象也存在光學(xué)和量子力學(xué)中. 隨后Kapitanski等[5]、Oskolkov[6-7]以及Taylor[8]對(duì)Talbot效應(yīng)進(jìn)行了分析. 2010年, Olver[9]研究了線(xiàn)性KdV方程在周期域上的初值條件為階梯函數(shù)時(shí), 發(fā)現(xiàn)其初邊值問(wèn)題的解滿(mǎn)足Talbot效應(yīng), 進(jìn)而將結(jié)論推廣到色散關(guān)系為整數(shù)多項(xiàng)式的線(xiàn)性色散方程中. Chen等[10]對(duì)初值條件為階梯函數(shù), 且具有一般色散關(guān)系的線(xiàn)性和非線(xiàn)性色散方程進(jìn)行了數(shù)值模擬, 從數(shù)值結(jié)果中得到對(duì)于線(xiàn)性色散方程, 色散關(guān)系的大波數(shù)漸近行為對(duì)周期域上的非光滑解的演化有決定性作用. 2021年, 尹子涵等[11]對(duì)二維線(xiàn)性KdV方程和Schr?dinger方程的周期初邊值問(wèn)題進(jìn)行了研究, 得出此類(lèi)方程的解存在色散量子化現(xiàn)象. 但對(duì)線(xiàn)性Boussinesq方程的研究鮮見(jiàn)報(bào)道.

本文基于文獻(xiàn)[10-11], 研究線(xiàn)性Boussinesq方程周期初邊值問(wèn)題解在大波數(shù)條件下的漸近行為. 首先研究色散關(guān)系為整數(shù)多項(xiàng)式和非整數(shù)多項(xiàng)式的一維線(xiàn)性Boussinesq方程的周期初邊值問(wèn)題; 然后研究二維線(xiàn)性Boussinesq方程的周期初邊值問(wèn)題. 給出存在色散量子化現(xiàn)象的線(xiàn)性Boussinesq方程的色散關(guān)系形式, 并研究在不同情況下方程周期解在大波數(shù)條件下的漸近行為.

1 一維線(xiàn)性Boussinesq方程

考慮定義在區(qū)間[0,2π]的Boussinesq方程的周期初邊值問(wèn)題:

方程的色散關(guān)系為:

將方程解展開(kāi)成Fourier級(jí)數(shù)形式:

式中:為奇數(shù).

進(jìn)一步研究色散關(guān)系為:

的Boussinesq方程的周期初邊值問(wèn)題.

考慮定義在區(qū)間[0,2π]的Boussinesq方程的周期初邊值問(wèn)題:

方程的色散關(guān)系為式(5).

將式(3)代入式(6), 得到方程:

求出色散關(guān)系式(5).

時(shí), 方程周期解的Fourier級(jí)數(shù)為:

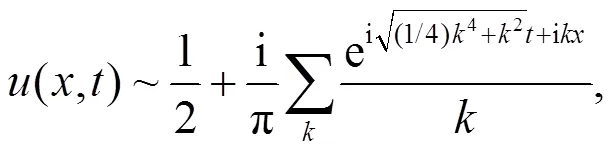
式中:為奇數(shù).

色散關(guān)系為:

時(shí), 方程周期解的Fourier級(jí)數(shù)為:

式中:為奇數(shù).

用Matlab軟件畫(huà)出色散關(guān)系為式(5)時(shí)方程解Fourier級(jí)數(shù)的實(shí)部和虛部前1000項(xiàng)和. 圖3和圖4是色散關(guān)系為式(7)時(shí)的結(jié)果; 圖5和圖6是色散關(guān)系為式(9)時(shí)的結(jié)果. 數(shù)值結(jié)果表明:在有理時(shí)刻方程解近似于分段常數(shù)函數(shù); 在無(wú)理時(shí)刻呈現(xiàn)分形化現(xiàn)象.

圖1

圖2

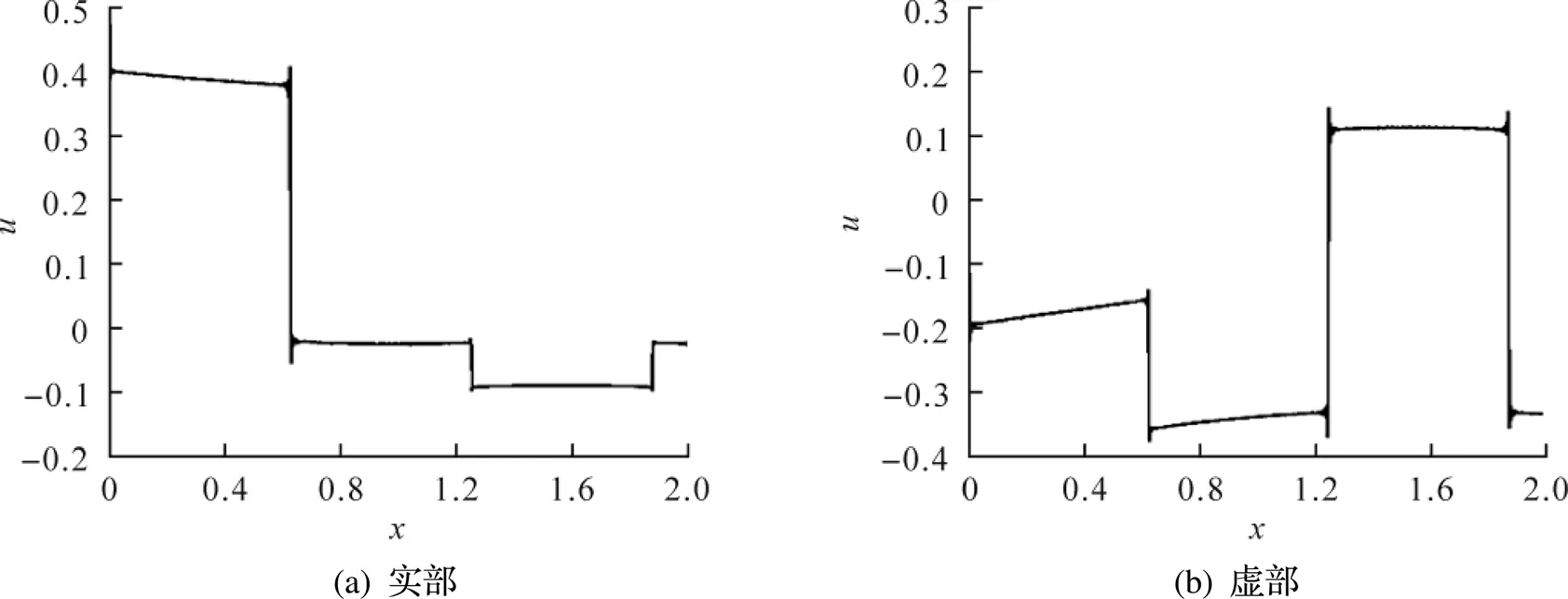
圖3

圖4

圖5

圖6

由于

從而在大波數(shù)條件下, 色散關(guān)系為式(5)方程解可以近似于色散關(guān)系為式(2)的方程解. 表明一維線(xiàn)性Boussinesq方程的周期解在大波數(shù)條件下的漸近行為由色散關(guān)系的漸近行為所控制. 這個(gè)結(jié)論可以推廣至二維線(xiàn)性色散方程的周期初邊值問(wèn)題.

2 二維線(xiàn)性Boussinesq方程

方程的色散關(guān)系為:

因?yàn)?/p>

將方程解展開(kāi)成二維Fourier級(jí)數(shù)形式:

將式(13)代入式(11)中, 得到方程:

求解式(14), 得到色散關(guān)系式(12).根據(jù)階梯函數(shù)得到色散關(guān)系為:

時(shí), 方程解的Fourier級(jí)數(shù)為:

式中:1和2為奇數(shù).

色散關(guān)系為:

時(shí), 方程解的Fourier級(jí)數(shù)為:

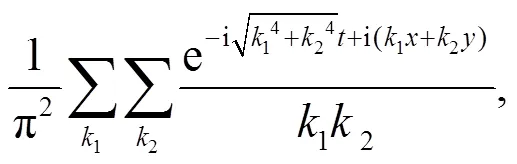
式中:1和2為奇數(shù).

用Matlab軟件畫(huà)出色散關(guān)系為式(14)的方程周期解Fourier級(jí)數(shù)的實(shí)部和虛部前100×100項(xiàng)和. 圖7和圖8為色散關(guān)系為式(15)時(shí)的結(jié)果; 圖9和圖10為色散關(guān)系為式(16)時(shí)的結(jié)果. 數(shù)值結(jié)果表明: 在有理時(shí)刻方程解為分片段常數(shù)形式; 在無(wú)理時(shí)刻方程解呈現(xiàn)分形化現(xiàn)象. 說(shuō)明色散關(guān)系為式(12)的二維線(xiàn)性Boussinesq方程存在色散量子化現(xiàn)象.

圖7

圖8

圖9

圖10

如果式(18)的色散關(guān)系為整數(shù)多項(xiàng)式, 則方程的周期初邊值問(wèn)題存在色散量子化現(xiàn)象.

方程的色散關(guān)系為:

將式(13)代入式(18)中, 得到方程:

求出色散關(guān)系式(19).

時(shí), 方程解的Fourier級(jí)數(shù)為:

式中:1和2為奇數(shù).

色散關(guān)系為:

時(shí),方程解的Fourier級(jí)數(shù)為:

式中:1和2為奇數(shù).

用Matlab軟件畫(huà)出色散關(guān)系為式(19)的方程周期解Fourier級(jí)數(shù)實(shí)部和虛部的前100×100項(xiàng)和. 圖11和圖12是當(dāng)色散關(guān)系為式(20)時(shí)的數(shù)值結(jié)果; 圖13和圖14是當(dāng)色散關(guān)系為式(21)時(shí)的數(shù)值結(jié)果. 數(shù)值結(jié)果表明:方程解在有理時(shí)刻近似為分片段常數(shù)函數(shù); 在無(wú)理時(shí)刻呈現(xiàn)分形化現(xiàn)象. 這與一維的情況相同.

類(lèi)似地, 因?yàn)?/p>

所以

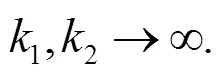
從而在大波數(shù)條件下, 色散關(guān)系為式(19)的方程解可以近似于色散關(guān)系為:

的方程解. 得到二維線(xiàn)性Boussinesq方程的周期解在大波數(shù)條件下的漸近行為由色散關(guān)系的漸近行為所控制. 這一結(jié)論可以推廣至二維線(xiàn)性色散方程的周期初邊值問(wèn)題.

圖11

圖12

圖13

圖14

3 結(jié)語(yǔ)

本文研究了線(xiàn)性Boussinesq方程的周期初邊值問(wèn)題解在大波數(shù)條件下的漸近行為, 首先計(jì)算出初值條件為階梯函數(shù)的線(xiàn)性Boussinesq方程解的Fourier級(jí)數(shù); 然后用Matlab軟件對(duì)不同色散關(guān)系的線(xiàn)性Boussinesq方程進(jìn)行數(shù)值模擬. 當(dāng)色散關(guān)系滿(mǎn)足整數(shù)多項(xiàng)式時(shí), 方程周期解存在色散量子化現(xiàn)象; 當(dāng)色散關(guān)系不滿(mǎn)足整數(shù)多項(xiàng)式時(shí), 方程周期解在大波數(shù)條件下的漸近行為存在色散量子化現(xiàn)象. 從而可知: 線(xiàn)性Boussinesq方程在大波數(shù)條件下的漸近行為受色散關(guān)系在大波數(shù)條件下的漸近行為控制.

[1] Berry M V. Quantum fractals in boxes[J]. Journal of Physics A: Mathematical and General, 1996, 29(20): 6617-6629.

[2] Talbot H F. Facts relating to optical science. No. IV[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1836, 9(56):401-407.

[3] Berry M V, Marzoli I, Schleich W. Quantum carpets, carpets of light[J]. Physics World, 2001, 14(6):39-46.

[4] Berry M V, Klein S. Integer, fractional and fractal Talbot effects[J]. Journal of Modern Optics, 1996, 43(10):2139- 2164.

[5] Kapitanski L, Rodnianski I. Does a quantum particle know the time?[M]//Emerging Applications of Number Theory. New York: Springer, 1999:355-371.

[6] Oskolkov K. Schr?dinger equation and oscillatory Hilbert transforms of second degree[J]. The Journal of Fourier Analysis and Applications, 1998, 4(3):341-356.

[7] Oskolkov K. A class of I. M. Vinogradov’s series and its applications in harmonic analysis[M]//Progress in Approximation Theory. New York: Springer, 1992:353-402.

[8] Taylor M. The Schr?dinger equation on spheres[J]. Pacific Journal of Mathematics, 2003, 209(1):145-155.

[9] Olver P J. Dispersive quantization[J]. The American Mathematical Monthly, 2010, 117(7):599-610.

[10] Chen G, Olver P J. Dispersion of discontinuous periodic waves[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2013, 469(2149):20120407.

[11] 尹子涵, 康靜. 二維線(xiàn)性色散方程的色散量子化現(xiàn)象[J]. 應(yīng)用數(shù)學(xué)和力學(xué), 2021, 42(7):741-750.

Dispersion quantization of linear Boussinesq equation

ZHANG Miaomiao, LI Maohua*

( School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China )

In this paper, we study the asymptotic behavior of solutions to periodic initial boundary value problem for linear Bousssinesq equation with large wave numbers. By expressing the solution of the equation in Fourier series, Matlab is used for numerical simulation. The simulation results show that the asymptotic behavior of the dispersion relation plays a decisive role in the asymptotic behavior of the solution of the equation on the condition of large wave numbers, which indicates that the dispersion quantization phenomenon exists in the linear Bousenisq equation.

linear Bousssinesq equation; periodic initial boundary value problem; dispersion relation; asymptotic behavior; quantization of dispersion

O29

A

1001-5132（2022）02-0027-08

2021?10?14.

寧波大學(xué)學(xué)報(bào)（理工版）網(wǎng)址: http://journallg.nbu.edu.cn/

國(guó)家自然科學(xué)基金（12111530003）; 寧波市自然科學(xué)基金（2018A610197）.

張苗苗（1995－）, 女, 甘肅天水人, 在讀碩士研究生, 主要研究方向: 可積系統(tǒng). E-mail: 3294140387@qq.com

李茂華（1973－）, 男, 浙江寧波人, 副教授, 主要研究方向: 可積系統(tǒng). E-mail: limaohua@nbu.edu.cn

（責(zé)任編輯 史小麗）