化難為簡數個數
秦浩然

周末,爸爸媽媽帶我去海邊玩。可是“天有不測風云”,臺風光顧,我們的游玩計劃泡了湯,只能窩在酒店里。
我百無聊賴地從酒店房間往外看,突然發現沙灘上有一塊巨大的電子屏幕。仔細一瞧,原來整個大屏幕是由一些長方形的小屏幕組成的。我趕緊把這一大發現告訴媽媽。媽媽問道:“如果把一塊小屏幕看成一個小長方形,你能算出這塊大屏幕里一共有多少個長方形嗎?”
這可難不倒我,我把這塊巨大屏幕的大概樣式畫在紙上。
數圖形要講究“不遺漏、不重復”的原則。我可以先數1個小長方形,再數由2個小長方形拼成的長方形,然后依次數由3個小長方形拼成的長方形、由4個小長方形拼成的長方形……細想一下,這樣一一列舉也太麻煩了,有沒有更加簡單的方法呢?
我仔細審視著紙上的圖形,發現圖形的第1行是由5個小長方形組成的。
這一行里一共有5個單個的小長方形、4個由2個小長方形組合成的長方形、3個由3個小長方形組合成的長方形、2個由4個小長方形組合成的長方形和1個由5個小長方形組合成的長方形,這樣第1行一共有5+4+3+2+1=15(個)長方形。大屏幕中一共有4行這樣的圖形,那就有15×4=60(個)長方形。
再把第1行、第2行合并看,如圖1。
忽略這個圖形中的虛線部分,那么和上述情況一樣共有15個長方形。而整個大屏幕中像這樣2行合并在一起的長方形有3個,即一共有15×3=45(個)長方形。
然后把第1行、第2行和第3行合并起來,如圖2。
同樣忽略圖形中的虛線部分,那么和上面一樣,也共有15個長方形。而整個大屏幕中像這樣3行合并在一起的長方形有2個,即一共有15×2=30(個)長方形。接著,把4行合并起來,如圖3。
同樣把圖形中的虛線部分忽略,數長方形的方法同上,共有15個長方形。這樣,整個大屏幕中長方形個數的總和為60+45+30+15=150(個)。
我激動極了,但是生怕出錯,想了想有沒有更好的方法。對了!其實在探究過程中我們不難發現,這個圖形每一行的長方形個數為15,正好是這些長方形的長的線段數。剛才我已經知道高為1行的長方形一共有4種,高為2行的長方形一共有3種,高為3行的長方形一共有2種,最后高為4行的長方形為1種。共有4+3+2+1=10(種)這樣的長方形,這正好是這些長方形的寬的線段數。最后,長方形的總個數就是長方形的長的線段數×長方形的寬的線段數=15×10=150(個)。
哈哈,這樣就更簡單了!不算不知道,一算嚇一跳,一個由20個小長方形組成的大長方形巨型屏幕竟然隱藏了這么多的長方形,真是太神奇了!這可能就是數學帶來的驚喜吧!
指導老師 陸 霞
李 軍? 3月4日? 11:19:32
浩然也太厲害了吧,去海邊玩也能從周邊的事物中發現一道數學題。果然,數學就是要靠仔細的觀察和嚴謹的思考,這樣才有機會像數學家那樣想出一個個厲害的數學定理。
劉朵朵? 3月4日? 14:18:10
浩然給出了2種數圖形的方法。一種是1行1行、2行2行……地數,另一種是利用線段的數量來數圖形。其中,數線段的重要規律是:單條線上線段的總數,都等于從1開始的幾個連續數的和(有幾條獨立線段就有幾個連續數)。這個數線段的規律,也可以擴展到數圖形上。
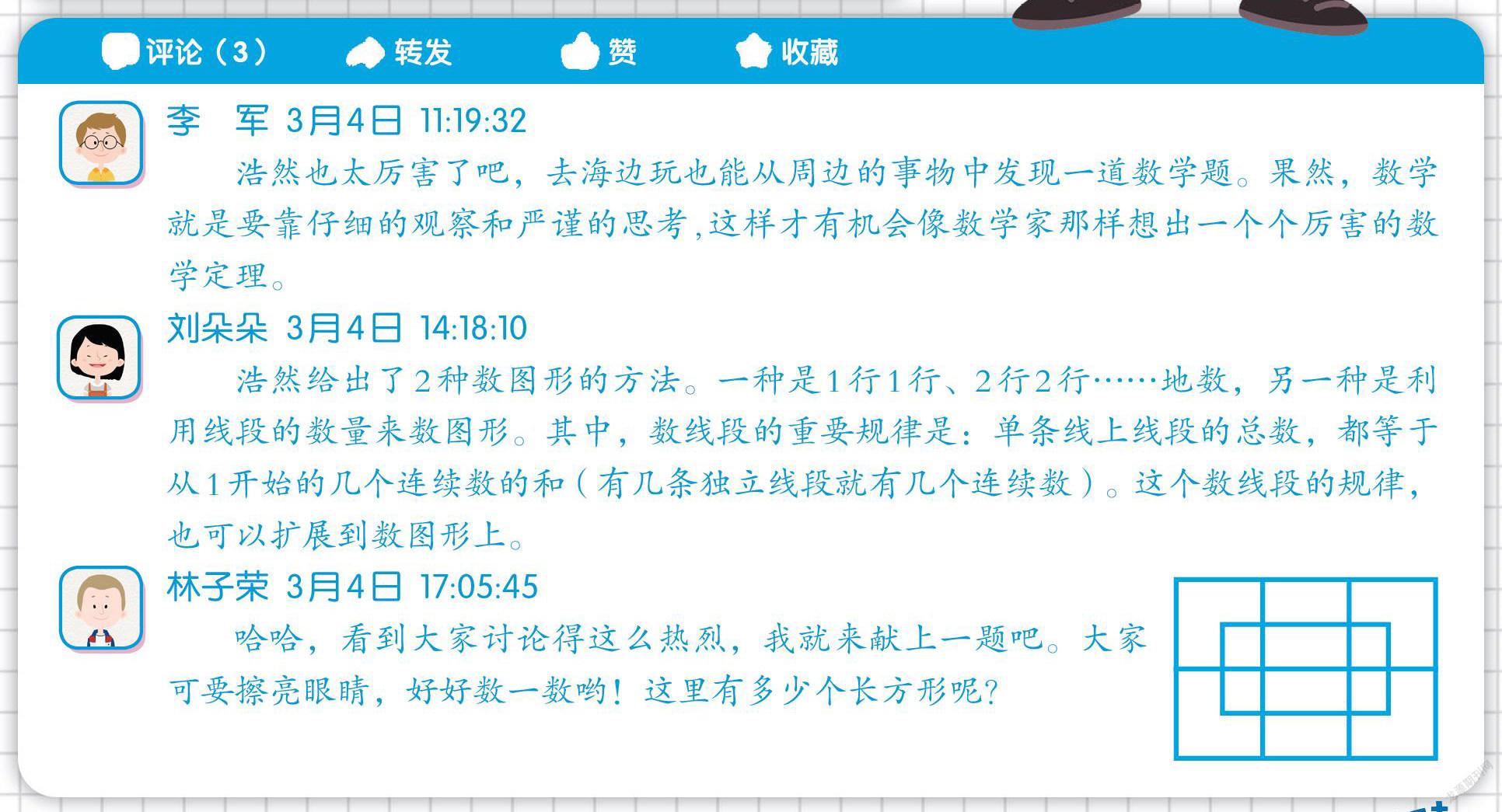
林子榮? 3月4日? 17:05:45
哈哈,看到大家討論得這么熱烈,我就來獻上一題吧。大家可要擦亮眼睛,好好數一數喲!這里有多少個長方形呢?
3025500316546

