基于貝葉斯參數優化的無模型自適應硅單晶直徑控制

林光偉，王 珊，張西亞，彭 鑫，高俊偉，高德東

(1.青海大學機械工程學院，西寧 810016； 2.陽光能源(青海)有限公司，西寧 810000)

0 引 言

直拉法硅單晶的制備直接推動了電子信息產業與光伏發電產業的飛速發展，但高新技術的突飛猛進對硅單晶提出了更高的品質要求，包括更大的晶體尺寸以及更均勻的直徑[1-2]。由于生產條件的限制，目前所生產的大尺寸硅單晶的有效直徑受到極大影響，因此解決這一問題是非常重要的。考慮到直拉硅單晶的生長過程涉及多場多相耦合與復雜的物理化學變化，有研究者發現在晶體生長過程中工藝參數不穩定容易引起硅單晶直徑波動，導致最終晶體的有效直徑減小。為此，研究人員進一步對影響硅單晶直徑波動的因素進行分析。Brown等[3]研究發現，坩堝上升速度以及籽晶棒的拉速不匹配會影響硅晶體的結晶速率，導致直徑不穩定。Gevelber等[4-5]提出，晶轉與堝轉速度差異較大，熔體渦流中心會與籽晶軸軸心偏離，導致硅晶體生長發生偏移，使硅晶體產生內部缺陷從而影響晶體直徑。Galazka等[6]通過分析直拉法制備硅單晶的熱傳導過程，發現不均衡的熱場溫度分布也會影響結晶速率，導致晶體的直徑大小受到一定的影響。國內學者劉丁等[7-8]總結提出，直徑均勻性與硅晶體內部的缺陷位錯有重要關系，直徑變化越大，晶體內部產生缺陷和位錯的可能性越大，導致硅晶體的品質下降，因此相對于追求更大尺寸的晶體，如何制備出均勻的直徑晶體更為重要。

直拉法制備硅單晶是在高溫高壓的環境中，持續通氬氣將高純度的多晶硅原料熔化，在單晶爐中完成引晶、放肩、等徑及收尾等過程[9]，最終形成硅晶體。但在具有多時變、大時滯、非線性及多場相互耦合的生長環境下，存在信息獲取難、測量難等問題，要制備出均勻的晶體直徑，就需要研究硅晶體生長過程中關鍵工藝參數的控制問題。因此，研究者分別從生長機理和PID控制原理出發，建立了晶體生長過程的控制基礎。生長機理控制是在對整個生長過程都研究分析透徹的基礎上建立的，因此Abdollahi等[10-12]就從基礎的晶體生長機理過程進行研究，建立了晶體生長過程中提拉速度影響晶體直徑變化的動力學幾何模型，并基于該模型設計了以提拉速度為輸入、晶體直徑為輸出的控制器，最后實現了通過調節提拉速度來控制晶體直徑的目的。而Winkler等[13-16]在分析前人提出的基于模型的多回路系統控制晶體直徑上，發現該系統用于控制時參數未知量太多，控制模型所達到的精度不夠，因此提出一種試圖克服這些局限性的控制系統，即通過忽略晶體生長過程中熱動力學過程的影響，僅主要考慮流體力學產生的重要作用，建立幾何模型，設計了針對晶體直徑和生長速度的雙閉環控制結構，通過控制工藝參數最終實現對晶體直徑的有效控制。但以上兩個具有重要影響力的學者所提出的控制過程及方法都涉及龐大的數學演算和推理，同時求解其中的數值解需要耗費大量的時間。而PID直徑控制是目前廣泛應用的控制手段，主要是通過控制加熱功率與提拉速度兩個工藝參數來實時調節晶體直徑。如圖1所示，當PID控制系統監測到設定直徑值與實際測量的晶體直徑值存在偏差時，會通過調節提拉速度控制晶體直徑，但在這個過程中響應速度會影響控制的精準性，因此利用溫度控制系統去對比實際溫度，適當彌補溫度之間的偏差進而與提拉速度共同控制晶體直徑[17-18]。但在實際的PID控制晶體生長過程中，監測的不準確以及反饋存在時滯是導致直徑控制效果降低的重要原因，因此學者們為提高最終的晶體品質，對PID直徑控制也進行研究分析。在使用CCD相機進行直徑檢測時存在較大的檢測誤差[19-20]，喬朝暉[21]將無味卡爾曼濾波技術應用于直拉法晶體生產過程中彎月面的高度估計，進而計算出晶體的直徑，并將此計算值用于替代CCD相機所反饋的晶體直徑，提高了控制精度。而張晶等[22]在利用熱場溫度進行PID控制的基礎上，設計廣義預測控制器重新對晶體的直徑進行控制，該控制器對直徑的檢測不準確方面有很好的改善。姜艦等[23]通過實驗分析不同PID控制參數對晶體生長的影響，并選取最優的PID控制參數進行實驗得到了更大更均勻的晶體直徑。以上學者對PID的直徑控制研究工作已經取得較大進展，但依然存在當硅單晶生長過程發生微小變動時，PID參數需要重新整定以及對生長過程復雜及參數眾多的硅單晶生長系統控制響應延遲的問題，因此，目前廣泛應用于直拉法制備硅單晶中的PID控制系統對直徑波動問題依舊沒有很好解決。

綜上，為實現均勻的晶體直徑所研究的直徑控制方法有基于機理模型的控制，也有在機理模型不準確、不確定性大時采用的PID直徑控制。然而硅單晶生長過程是一個集總參數的大系統，任何微小參數的波動都會影響晶體生長，導致最終的晶體直徑仍發生較大的波動。因此，針對生長機理控制以及PID直徑控制存在的缺陷，本文采用基于數據驅動的無模型自適應(model-free adaptive control, MFAC)方法進行直徑控制，通過分析晶體生長過程中復雜的生長環境及多參數共同作用的情況，將晶體生長過程中的工藝參數，即加熱器功率與坩堝上升速度作為輸入，晶體直徑數據作為輸出建立非線性系統，并在此基礎上實現晶體直徑的控制。雖然MFAC直徑控制能解決晶體生長模型未知以及大時變、大時滯的問題，但在控制模型的建立過程中引入的超參數也會影響直徑的控制過程，因此為實現硅單晶生長過程中直徑的準確控制，本文提出基于貝葉斯參數優化的MFAC直徑控制模型，并通過MATLAB仿真實驗結果證明了控制模型的有效性和優越性。

圖1 PID控制晶體生長系統演示Fig.1 Demonstration of PID control crystal growth system

1 硅單晶直徑控制模型建立

要實現對硅單晶直徑的控制，需要先明確控制的工藝參數。在硅單晶生長過程中，影響晶體直徑的工藝參數較多，在PID控制時常采用提拉速度與加熱器的功率作為控制參數，這是因為這兩個參數易于監測，如圖1所示，加熱器的功率輸出可以通過電壓電流控制，提拉速度可以通過伺服電機控制。但通過分析發現，提拉速度的監測裝置安裝在與籽晶軸連接的伺服電機上，在硅單晶生長過程中籽晶軸會受到氬氣吹拂從而影響監測數據，同時當籽晶軸提拉的晶體處于硅熔體中時，晶體旋轉中心與硅熔體的旋轉中心處于不同軸心時也會導致所監測的提拉速度發生偏差。因此，結合上述原因，考慮同樣易于監測與控制的坩堝上升速度來代替提拉速度。這是由于坩堝中的硅熔體在生長過程中會不斷轉化為固態而被籽晶提起，液面在坩堝中的位置也會不斷下降，所以當給予合適的堝升速度來保持液面在熱場中的相對位置不變時，能穩定固液界面處的溫度梯度，進一步實現硅單晶生長的平穩進行，避免硅單晶直徑出現大的波動，同時控制坩堝上升速度的伺服電機安裝在坩堝堝幫的底部，在伺服電機的工作中受到的影響相對提拉位置更小。因此在本文中為提高控制參數的準確性，選擇坩堝上升速度與加熱器功率作為控制參數，建立硅單晶直徑控制模型。

1.1 控制算法

硅單晶的生長是個復雜的非線性離散系統，通過機理控制以及PID控制都存在難題，因此，避開對硅晶體生長過程分析，考慮選取坩堝上升速度與加熱器的功率數據作為控制的輸入，硅單晶直徑作為輸出。根據侯忠生教授等[24-26]所提出的MFAC控制，引入偽雅克比矩陣(pseudo Jacobian matrix, PJM)將上述明確的以坩堝上升速度與加熱器的功率作為輸入、硅單晶直徑作為輸出的非線性離散系統等價轉化為虛擬的、動態的線性數值模型，進一步實現對硅晶體生長未知系統的MFAC控制。

首先，對雙輸入、多輸出非線性離散系統進行分析。

(1)

假設1：f(·)關于當前控制輸入信號u(k)的偏導數是連續的。

Δy(k+1)=ΦTΔU(k)

(2)

u(k)=u(k-1)+[y*(k+1)-y(k)]·ρΦ(k)/(λ+Φ2(k))

(3)

(4)

(5)

式中：ε為無窮小的數，表示該重置算法的引入能進一步保證在時變系統中依然保持很強的控制能力；u(k)為k時刻硅單晶生長中坩堝上升速度與加熱器的功率的輸入；y(k)為k時刻晶體直徑的輸出，通過設定初始時刻的工藝參數及晶體直徑數值可實現對晶體直徑的控制。

1.2 穩定性分析

對于硅單晶直徑控制模型，在滿足y(k+1)關于y(k)和坩堝上升速度與加熱器功率u(k)的偏導數連續且滿足廣義Lipschitz的條件下，當y*(k+1)和y(k+1)相等且為一個定值常量時，控制算法式(5)達到穩定，此時存在a>0保證系統的跟蹤誤差收斂且輸入輸出均有界，穩定性分析證明如下。

(6)

(7)

存在步長因子η∈(0,1]，μ>0，此時有

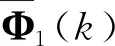
由e(k)=y*(k)-y(k)為控制輸出的誤差值，則

(8)

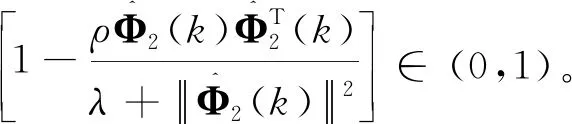
1.3 動態控制過程

式(5)建立了硅單晶直徑的控制算法，同時證明了該算法的穩定性，但在硅單晶生長中，對于控制的輸入輸出數據都要實時產生的，因此為了模擬實時控制的條件，在上述MFAC控制算法的基礎上需引入實時的硅單晶生長中直徑變化值。

考慮到直接采用實際拉晶過程中的直徑數據時，數據量過于龐大同時很難導入控制算法中，因此本文根據CL120-97爐的已有數據，建立了以堝升速度與加熱器功率作為輸入，晶體直徑作為輸出的擬合函數，該函數能為控制過程提供連續的直徑變化數據，并且將該擬合函數嵌入MFAC算法中更容易實現。本文中選取了1 200組實時生產數據，在表1中只顯示部分數據。由于擬合的精確度對控制過程沒有影響，對于2個自變量與1個因變量的擬合函數中常采用的是二次非線性擬合，因此，得到擬合函數表達式為：

(9)

式中：u1代表坩堝的上升速度；u2代表加熱器的輸出功率；y代表晶體直徑。通過該表達式，模擬出了在實際晶體生長中會出現的直徑變化情況。同時在結合式(3)的基礎上，將式(9)中模擬出的直徑值作為y(k)的變化值，進一步實現對實時硅單晶直徑的控制。

表1 晶體生長數據Table 1 Crystal growth data

因此，在式(5)MFAC控制算法的基礎上，令u=[u1u2]，Φ=[φ1φ2]T，得到雙輸入、單輸出MFAC動態控制算法為：

(10)

在硅單晶直徑控制過程中，用簡化的示意圖表示算法過程，如圖2所示。在給定初始k=1時刻的偽偏導數Φ(1)，控制輸入u1(1)u2(1)及k=1,2時刻硅單晶直徑y(1)y(2)的前提下，可以計算出k=3時刻的硅單晶直徑y(3)，此時對比設定的晶體直徑與控制輸出直徑的差值，即y*-y(3)的大小，來調節k=2時刻的偽偏導數Φ(2)與控制輸入u1(2)u2(2)，進一步計算下一時刻k=4時刻的硅單晶直徑y(4)，上述過程不斷迭代計算，最終計算到k時刻，y*-y(k)的值接近0或等于0時，晶體直徑達到設定值，此時控制算法穩定運行，實現了對晶體直徑的有效控制。

圖2 直徑控制算法動態演示Fig.2 Dynamic demonstration of diameter control algorithm

2 基于貝葉斯的超參數優化

2.1 超參數的影響

在硅單晶直徑控制模型中存在的超參數ρ、η、μ、λ需要進行初始設定，這些超參數對于控制模型的性能都有影響，并且不同的初始設定參數會帶來不同的計算量與時間成本，但滿足控制要求的合理設定范圍卻很難獲得。

在MFAC參數整定的研究[29-30]中發現四個超參數的敏感程度依次為λ>η>μ>ρ，因此為了降低超參數調整的復雜度，選取敏感程度較高的λ,η兩個超參數進行MATLAB仿真實驗，以驗證本文中超參數對硅單晶直徑控制的影響。

在進行仿真實驗前，設定目標晶體直徑為230 mm，并根據實際數據設定以下初始值：

y(1)=224.7,y(2)=223.1,u1(1)=0.161 0,Δu1(1)=-0.012,u2(1)=45.19,Δu2(1)=-0.05

而對于超參數的初始設定是根據參數整定研究中所得到的有效值并進行隨機組合，并且λ∈(0,2],η∈(0,1]，因此初始設定值為：

λ=0.5,η=0.5,μ=0.5,ρ=0.4,φ1=0,φ2=0.15;λ=1.0,η=0.2,μ=0.5,ρ=0.4,φ1=0,φ2=0.15;λ=1.1,η=0.8,μ=0.5,ρ=0.4,φ1=0,φ2=0.15;λ=1.3,η=0.2,μ=0.5,ρ=0.4,φ1=0,φ2=0.15;λ=1.5,η=0.3,μ=0.5,ρ=0.4,φ1=0,φ2=0.15

通過仿真實驗，得到實驗結果如圖3～5所示。圖3是在不同的超參數組合下，硅晶體直徑的控制結果，可以看出晶體直徑最終都達到均勻穩定的狀態，但超參數對整個控制過程有重要影響。同時從圖3中可發現，超參數不同的取值會影響直徑達到穩定的迭代次數，也會影響控制過程中的波動情況，也就是說用于實際晶體生長控制時，晶體達到穩定直徑的耗時較長，并且在晶體生長的初始階段，晶體的直徑變動范圍較大。

圖4是 MFAC控制模型對堝升速度與加熱器功率的控制結果。可以看出在160次迭代后，對于硅單晶生長過程中輸入的控制均達到了穩定狀態。但此時由于超參數的取值不同，最大的加熱器功率輸入達到了57.347 1 kW，最小的加熱器功率輸入為39.847 5 kW，兩者相差較大，表明超參數對生長過程中的輸入功率也有較大影響，用于實際生產時一定會影響成本的波動。同時從圖4中可以發現，最大的坩堝上升速度輸入在合理的范圍，但最小的坩堝上升速度輸入小于0，表明此時的控制效果很差，維持最小的坩堝上升速度輸入時對整個晶體生長過程都有負面影響。

圖3 控制晶體直徑的仿真結果Fig.3 Simulation results of controlling crystal diameter

圖5是直徑誤差結果，可以看出存在最大誤差與最小誤差的比值達到40倍的情況，也存在500次迭代過程中還沒收斂的情況。表明采用硅單晶直徑控制的效果與超參數的取值有密切關系，如何調整超參數會直接影響到硅單晶生長過程中的直徑波動范圍，以致影響最終的硅晶體品質。

圖4 控制輸入的仿真結果Fig.4 Simulation results of controlling input

圖5 控制晶體直徑的誤差結果Fig.5 Error results of controlling crystal diameter

從圖3～5中可以得出，MFAC硅單晶直徑控制模型達到了控制晶體直徑的作用，在數次迭代后都維持了穩定的控制，但也同樣得出超參數對控制的重要影響。總結以上結果，如表2所示。

表2 仿真結果數據Table 2 Simulation result data

從表2中可以得出，硅單晶直徑控制模型能夠實現對于晶體直徑的均勻控制，同時穩定硅晶體生長過程，但在實際的晶體生長過程中，坩堝的上升速度是0.1～0.3 cm/min，加熱器功率是44～48 kW，表明由于超參數的存在，控制輸入的數據已經超出合理的工藝參數范圍，必定會影響整個硅晶體生長過程。另外，直徑控制模型中超參數的取值不同，仿真過程的迭代次數太多，耗費的時間也會增加，導致在晶體生長的初始階段，晶體的直徑也會產生較大的波動從而影響最終的晶體品質。因此，在對MFAC硅單晶直徑控制模型進行仿真實現后得出，控制模型中涉及的超參數λ、η對整個硅單晶生長過程有重要影響。

2.2 貝葉斯參數優化

硅單晶直徑控制模型中的超參數是影響最終控制效果的重要因素，優化超參數λ,η來降低迭代次數并將輸入參數控制在一定范圍內，是實現硅單晶品質的提升過程中需要解決的問題。

在超參數優化的研究中，基礎的方法是手動調參、網格搜索及隨機搜索調參，其原理都是窮舉法，而在深度學習迅速發展后，許多研究者開始采用模擬退火算法、遺傳算法及粒子群優化算法等進化算法進行調優，另外還有基于梯度的參數優化算法等[31-32]。在本文中，采用以上優化方法迭代次數多、效率低，同時需要大規模的數據集，花費的代價太大。因此，選用迭代過程簡單、目標函數少、效率更高的貝葉斯優化對以上超參數進行調優。

貝葉斯優化的核心是先驗函數(prior function, PF)與采集函數(acquisition function, AC)。PF主要采用高斯過程回歸，利用高斯過程增加后驗概率的準確，而AC的函數中采用目前最為廣泛的EI(expected improvement, EI)，目的是探索方差最大的位置尋找最優[33]。

首先將上述5次仿真實驗的數據樣本擬合成高斯回歸模型，如式(11)所示：

f(x)=gp(0,k)

(11)

式中：k=(x,x′)為協方差函數，而x=[λη]是本文需要優化的λ,η兩個超參數。因此手動設置5次仿真實驗樣本值{(x1,y1),(x2,y2),…,(x5,y5)}，得到的協方差矩陣為式(12)：

(12)

Pm+1～N(μ,σ2)
μ=kTK-1fm(x)
σ2=k(xm+1,xm+1)-kTK-1k

(13)

根據上述高斯過程得到的后驗概率，再進一步通過采集函數EI決定下一個采樣點xm+1的選取。而EI函數依然采用explore和exploit兩種策略[34]，并求取未知點與f(x)差值的期望來評估是否進行選取該點。其準則函數表示為式(14)：

(14)

為更加直觀觀測整個優化過程，本文中采用三維視角，將需要優化的超參數λ、η設置為三維坐標系中的x軸與y軸，而目標位置與設定直徑差值f(x)-230設置為z軸。如圖7所示，每個已知點符合高斯過程的正態分布，進而通過計算方差與均值不斷接近理想的位置，最后尋找到最優的超參數范圍。

由于MFAC硅單晶直徑控制模型中需要優化的超參數λ∈(0,2],η∈(0,1]，因此該優化過程是連續的超參數尋優，可假定為二維平面內進行隨機的λ、η選取。然而在本文已經手動輸入一部分已知參數點的情況下，可以直接利用已知點的集合，并根據EI準則進行下一個點采樣。因此通過MTALAB軟件對上述貝葉斯優化過程進行仿真，最終得到的優化結果是λ∈[0.94,1.05],η∈(0,0.18]。

圖6 算法流程框圖Fig.6 Algorithm flow diagram

圖7 貝葉斯參數優化過程演示Fig.7 Demonstration of Bayesian parameter optimization process

3 硅單晶直徑控制的仿真實驗

在通過首次仿真實驗后發現，對超參數的優化是必要的，因此將貝葉斯參數優化得到的結果進行最終的硅單晶直徑控制的仿真實驗。

在進行仿真實驗前，設定目標晶體直徑為230 mm，并同樣根據實際數據設定以下初始值：y(1)=224.7,y(2)=223.1,u1(1)=0.161 0,Δu1(1)=-0.012,u2(1)=45.19,Δu2(1)=-0.05。

根據超參數優化的合理取值范圍，選取λ,η優化區間的最小值設定初始值，其他參數固定不變：λ=0.94,η=0,μ=0.5,ρ=0.4,φ1=0,φ2=0.15。

通過MATLAB軟件仿真得到優化后實驗結果對比如圖8、圖9所示。

圖8 貝葉斯參數優化后的直徑控制結果對比Fig.8 Comparison of diameter control results after Bayesian parameter optimization

通過貝葉斯超參數優化后的取值范圍，選取優化區間的最小值，得到直徑控制結果對比如圖8。可以發現在迭代4次后直徑就達到了設定的理想直徑，相對于沒有采用超參數優化前的迭代次數減少了250次以上，同時所耗費的時間成本也為優化前的1/100左右，達到了不錯的優化效果。

為了驗證貝葉斯優化后超參數取值范圍的有效性，進一步選取優化區間的最大值進行軟件仿真。同樣重新進行仿真實驗參數的初始化：y(1)=224.7,y(2)=223.1,u1(1)=0.161 0,Δu1(1)=-0.012,u2(1)=45.19,Δu2(1)=-0.05;λ=1.05,η=0.18,μ=0.5,ρ=0.4,φ1=0,φ2=0.15。

設定目標晶體直徑為230 mm，軟件仿真得到優化前后實驗結果對比如圖9。

圖9 貝葉斯參數優化后的直徑控制結果對比Fig.9 Comparison of diameter controlling results after Bayesian parameter optimization

通過圖9發現，選取超參數優化區間的最大值進行仿真，迭代次數在7次時，晶體的直徑也達到穩定，相對于沒有采用超參數優化前的迭代次數減少了245次以上。因此表明采用貝葉斯超參數優化后，MFAC硅單晶直徑控制模型降低了計算量，減少了直徑控制時間，達到了更好的控制效果。

同時采用貝葉斯優化超參數進行軟件仿真后的直徑誤差和控制輸入結果如圖10、圖11。從圖10可以發現，采用貝葉斯對超參數優化后，整個控制過程中的晶體直徑誤差值最大僅有1.227 6 mm，而最小只有0.168 6 mm，在實際的晶體直徑測量中都可以作為測量誤差忽略，達到了不錯的直徑控制效果。同時通過圖11對比分析優化前后的控制輸入結果發現，在晶體直徑達到穩定值之后，控制輸入參數u1的最大值為0.215 9 cm/min，最小值為0.161 0 cm/min，而控制輸入參數u2最大值為46.623 3 kW，最小值為45.407 2 kW，滿足實際晶體生長中坩堝的上升速度在0.1～0.3 cm/min，加熱器功率在44～47 kW的合理范圍要求，實現了晶體生長過程中工藝參數得到優化的提升，同時降低了生產過程的成本，以較低的加熱器功率和較低的坩堝上升速度生產出優質的硅單晶，表明整個控制模型在超參數優下，達到了最佳的直徑控制效果。對比貝葉斯超參數優化區間的最小值與最大值發現，晶體直徑控制的迭代次數有差異，即控制過程中穩定晶體直徑的時長存在差異，選取更小的超參數組合時花費的時間更少，達到穩定直徑的過程更快，而值更大的超參數組合達到穩定直徑的時間更長。同時超參數的值過小會降低坩堝的上升速度和加熱器功率，反之超參數的值更大會適當地增大坩堝的上升速度和加熱器的功率。然而，在晶體的生長過程中，更小的坩堝上升速度與加熱器功率會增加晶體生在的整體時長，對于批量生產晶體來說，會累計增加生產成本。因此對于不同的生產要求，在控制晶體生長時，應該采用不同的超參數組合里來滿足要求。

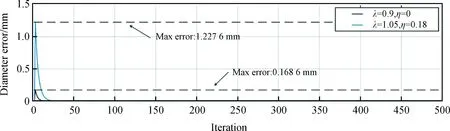
圖10 貝葉斯參數優化后的直徑控制誤差結果Fig.10 Diameter controlling error results after Bayesian parameter optimization

圖11 貝葉斯參數優化后的控制輸入結果Fig.11 Controlling input results after Bayesian parameter optimization

針對MFAC控制應用于直拉法硅單晶生長過程控制中存在的問題，通過采用貝葉斯參數優化將MFAC硅單晶直徑控制算法進行了優化，并重新進行軟件仿真，解決了控制過程中存在的計算量和迭代時間的問題，得到了更好的控制效果。表明基于貝葉斯參數優化下的MFAC硅單晶直徑控制模型應用于解決晶體直徑有不錯的效果，不僅將直徑控制誤差最小降低至0.168 6 mm，同時實現了生產成本的降低。

4 結 論

硅單晶直徑的均勻性是影響晶體品質的重要因素之一，如何更好地實現直拉法硅單晶生長過程的直徑控制，得到更加均勻的直徑一直是晶硅生長領域關注的熱點。因此通過分析已有的直徑控制方法后，本文提出了MFAC硅單晶直徑控制方法。并在根據此控制算法進行軟件仿真后發現，控制算法中涉及的超參數對整個控制過程有一定的影響，進而利用貝葉斯參數優化法對超參數進行了優化，確定了超參數的合理范圍。對基于貝葉斯參數優化下的MFAC控制算法重新進行軟件仿真，驗證優化后的超參數有效提高控制效果。MFAC硅單晶直徑控制模型解決了機理建模控制和PID控制存在的問題，表現出更好的直徑控制能力，而且能夠在算法優化后，提高硅單晶生長的穩定性，降低硅單晶生產成本，具有良好的應用前景。