借助于有效的教學模式構建和諧高效的課堂
繆樹模
[摘 ?要] 為了進一步突破應試教育的束縛,培養出具有獨創精神的新型人才,在初中數學教學中既要突出學生的主體作用,又要重視教師的主導價值,協調好“教”與“學”的關系,堅持“教”與“學”協同發展,實現教學相長.
[關鍵詞] 主體作用;主導價值;教學相長
在素質教育的影響下,初中數學教學模式、教師手段、教學方法日益豐富化、多樣化. “三環三學”的新型教學模式改變了以“傳授”為主的教學現狀,體現了教師為主導、學生為主體、訓練為主線的原則,其有助于提高教學有效性,促進師生和諧發展. 另外,為了使課堂更高效,在課堂教學中可以遵循“五步法”,即“溫故知新—自學質疑—細讀研學—拓展延伸—總結概括”,進而順著學生的思維脈絡,借助于循序漸進的引導,建構和諧高效的數學課堂. 筆者以“最大利潤”為例,展現了“三環三學”教學模式的優勢,并在研學環節堅持“以生為主”,借助于“五步法”喚醒了學生的主體意識,取得了較好的教學效果,現在將一些心得體會分享給大家,以期共鑒.
預習環節
預習環節顧名思義就是課前策劃,即教師依據教學目標和實際學情設計預習目標,制定預習導學單,根據導學內容既可以幫助學生鞏固舊知識,為探究新知識掃清思維障礙,又可以讓學生課前就可以對本節的教學重難點形成初步認識,有效提高聽課效率. 同時,在預習環節,教師可以鼓勵學生進行合作學習,這樣通過課堂爭辯、交流、合作,學生往往可以總結歸納出許多有價值的資源,不僅可以豐富課堂教學內容,而且有利于發現型、創新型課堂的建構. 可見,課前策劃在數學教學中具有重要的價值,是教學的重要組成部分之一,應引起一線教師的高度重視. 當然,要使課前策劃能夠發揮其特有的優勢,教師應以“三個理解”為基礎,設計具有針對性和前瞻性的預習內容,從而在明確目標的指引下開展有意義的教學,提升教學有效性.
研學環節
在“利潤最大”的研學環節,筆者結合教學內容和具體學情,通過“五步法”充分挖掘學生的內在潛能,引導學生學會自學、學會合作、學會探究,從而輕松地掌握了新知識,實現了新發展.
1. 溫故知新
本節內容與生活息息相關,因而在此環節教師可以采用情境引入法,借助于生活問題誘發學生聯系舊知識去思考新問題,從而拉近“新”與“舊”的距離,提升學生的學習信心.
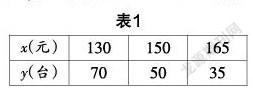
例1 ?某產品的成本價為120元/臺,在試營業階段,每件售價x(元)與日銷售量y(臺)的函數關系如表1所示. (日銷售量y是每件售價x的一次函數)
(1)寫出y與x的函數關系式;
(2)如果你是老板,你會如何給商品定價?
筆者出示第(2)問后,學生的探究熱情被迅速激發了,個個爭當聰明的老板,課堂氣氛活躍了起來. 在此過程中既復習了一次函數解析式的求法,又為接下來二次函數最值的探究做好了鋪墊. 這樣以生活情境引入新知識“利潤最大”的教學自然得體,同時借助于實際應用,更能彰顯數學學習的價值.
2. 自學質疑
為了引導學生能夠自己總結歸納出一些有價值的東西,在此環節教師可以列舉一些具體的題目,引導學生在解決問題的過程中理性地認識問題規律,培養學生自主發現、自主探究的優良學習品質.
例2 ?某商品的進價為10元/件,售價為15元/件,則每件商品的利潤是____元.
(1)若漲價2元,則售價為____元,利潤為____元;
(2)若漲價3元,則售價為____元,利潤為____元;
(3)若漲價x元,則售價為____元,利潤為____元;
(4)若降價x元,則售價為____元,利潤為____元.
設計意圖 ?借助于簡單的生活實例引導學生總結歸納出利潤與成本和售價的對應關系.
例3 ?某商品原來每天可賣出100件,為了獲得更高的利潤,經市場調研發現:若該產品每降價1元,則多賣出2件;若每漲價1元,則少賣出2件.
(1)若每降價2元,則多賣出____件,日銷售量為____件;
(2)若每降價x元,則多賣出____件,日銷售量為____件;
(3)若每漲價5元,則少賣出____件,日銷售量為____件;
(4)若每漲價x元,則少賣出____件,日銷售量為____件.
設計意圖 ?引導學生總結歸納出總利潤與銷售量和單件商品利潤的對應關系.
這樣通過簡單的、熟悉的問題引導學生總結歸納出了本節課兩個重要的等量關系,為后面“最大利潤”的探究做好了充足的準備.
3. 細讀研學
在此環節,先在教師的帶領下,借助于典型的例習題的示范功能幫助學生理清知識要點,解除心中疑惑,形成解題規范;接下來讓學生獨立完成一定量的基礎練習,通過“練”讓學生發現問題,并通過合作交流或教師點撥解決問題,以此既能引導學生獨立思考,又能讓學生在互幫互助中不斷提升自己、發展自己,從而讓每個學生都能有所收獲.
例4 ?某商品進價為40元/件,現售價為60元/件,每周的銷售量為300件,根據市場調研發現,若每漲價1元,則每周少賣10件.
(1)寫出銷售利潤y(元)與漲價x(元)的函數關系;
(2)當漲價x(元)為何值時,銷售利潤y(元)最大?最大利潤是多少?
(3)最終售價為多少元時,可以使得銷售利潤y(元)最大?最大利潤是多少?
有了前面例題的鋪墊,例4對于學生來說并不陌生,可以引導學生先獨立思考,這樣可以在“研學”的過程中滲透“驗學”. 學生的基本思路形成后,教師可以帶領學生共同完成問題的解決,在此環節要充分展示學生的思維過程. 為了使溝通更有效,教師可以將問題改編成問題組,使之轉化為學生熟悉的內容. 如先讓學生思考“漲價2元時,賣出的商品件數與銷售利潤的關系”,接下來按照這個思路探究“漲價x(元)時,銷售利潤y(元)與漲價x(元)的函數關系”,這樣通過循序漸進地引導幫助學生深化新知識的理解.
設計意圖 ?借助于例題趁熱打鐵,通過例題的精講幫助學生形成解題規范,加深學生對新知識的理解,同時引導學生學會用新知識去解決實際問題. 以上三個問題由易到難,層層遞進,是在學生原有認知基礎上的建構,符合學生的認知發展規律,有利于提升課堂有效性.
4. 拓展延伸
學生通過以上環節理解并應用了新知識,為了進一步強化理解,教師可以充分發揮變式練習的拓展延伸的功能,借助于“變”培養思維的靈活性,實現知識的融會貫通.
例如,對于例4,可以將“漲價”變為“降價”,將“少賣”變為“多賣”,讓學生在解決實際問題的過程中進一步理解“總利潤=銷售量×每件利潤”,進而將知識點有效地串聯起來,提升實際應用能力.
5. 總結概括
總結概括可謂是一節課的點睛之筆,在此環節引導學生將點滴的收獲總結歸納為學習經驗,這樣不僅可以幫助學生理清本節課的重難點,而且通過有效的回顧可以加深對知識的理解. 另外,在此環節還可以引導學生通過相似、相關問題的聯想,將新知識納入原有的知識體系,實現認知的完善與優化.
當然,“五步法”并非一成不變,在實際教學中還是需要教師結合具體的學情和教學內容進行適當的調整,不過無論如何調整都應協調好“教”與“學”的關系,要注意把握課堂的靈活性、創新性.
驗學環節
1. 回歸課本,總結升華
經歷了預習環節和研學環節,為了進一步幫助學生升華所學,教師可以隨堂進行檢測,當然題目的設計應遵循“低起點、小坡度”的原則,這樣既能驅動每個學生解決問題,又能讓學生提升不同程度的應用能力,實現“穩中求進、差中求異”的效果.
2. 優化知識,拓展提升
在學習中既要回歸課本,掌握“雙基”,又要跳出課本,帶領學生回歸生活,從而讓學生體驗“學以致用”的真諦,以此優化學生的知識結構,提升學生的數學應用能力. 在此環節,教師設計檢測試題或作業時不能拘泥于課本,而應結合學生的實際生活設計一些符合學生認知的問題,以此讓學生在“吃得飽”的基礎上“吃得好”,通過新拓展實現“優中求精”的目的.
3. 多元評價,激發熱情
在研學環節,教師應結合實際學情、教學內容、課堂表現給予學生準確的、及時的評價,側重發揮課堂評價的激勵作用,以此提高學生的自信心,提升其數學學習興趣. 其實,研學環節往往滲透于“預習”和“研學”中,貫穿教學始終,通過巧妙的“驗”可使“教”與“學”變得更高效.
總之,在實際教學中,要改變傳統的教學觀念的束縛,重視發揮學生的主體作用,讓學生在“活動”中學習,在“探究”中提升,在“合作”中成長,進而營造一個和諧高效的數學課堂.
3935501908210

