某山區(qū)人行廊橋三分力系數(shù)風洞實驗研究

王可峰，陳 濤，蘇 益

（1.中國市政工程西南設計研究總院有限公司，四川 成都610081；2.西南交通大學風工程試驗研究中心，四川 成都610031；3.西南交通大學風工程四川省重點實驗室，四川 成都 610031）

0 引言

長懸挑結構是現(xiàn)代建筑結構設計技術發(fā)展成果的重要組成部分，被廣泛應用于高層建筑、觀景平臺、體育場館等建筑。隨著設計理念及施工技術的進步與發(fā)展，建筑工程結構的功能、造型及技術越發(fā)復雜多樣，應用的設計方法及施工手段也與日俱進，山區(qū)風環(huán)境下各類新型建筑結構的抗風性能則需被特殊關注。其中靜力三分力系數(shù)研究是結構抗風性能研究中的基礎性工作。根據(jù)結構靜力三分力系數(shù)，可以算得作用于結構的三分力（升力、阻力、扭矩），進而研究靜風荷載作用下結構風致響應，并進行靜風穩(wěn)定性分析。

目前國內(nèi)對懸挑結構的研究方向普遍集中在懸挑結構的施工吊裝及卸載分析[1]、抗震性能分析[2-3]、舒適性分析與控制[4]和風荷載分析[5]，對于山區(qū)地帶懸挑式結構的研究則主要偏向于其對于道路擴寬的作用，而對于山區(qū)峽谷地帶懸挑式觀景橋的抗風性能及設計的研究極少[6]。

隨著特殊山區(qū)旅游事業(yè)的發(fā)展，最近幾年各地出現(xiàn)數(shù)座山區(qū)懸挑觀景廊橋正在設計、建造中或已使用，且懸臂長度不斷增大，結構形式越發(fā)新奇。根據(jù)對橋梁抗風性能的不斷研究，風致效應敏感的橋梁不單限于大跨度橋梁，諸如特殊人行橋等諸多形式的短、中跨橋梁亦列為風致效應敏感的結構中[7]。然而國內(nèi)外關于此類人行橋梁結構抗風性能的研究極少[8-9]，如某些山區(qū)高懸崖處長懸挑觀景廊橋結構，其結構形式及所處風環(huán)境與一般意義上的橋梁結構存在諸多差異，風荷載作用下風致響應情況更加復雜，導致相應的規(guī)范及標準中尚未規(guī)定及明確其設計參數(shù)，同時值得借鑒的類似研究成果極少，當前仍需要通過風洞實驗等方法進行分析。

考慮到山地地形復雜多變的特點，局部風環(huán)境的影響因素較多，深入研究橋位處風環(huán)境是山區(qū)橋梁抗風設計的基礎，諸如平均風速、風偏角、風攻角等各風特性參數(shù)均對三分力系數(shù)存在一定的影響。本文以遼寧蒲石河楓葉觀景橋為依托，進行剛性模型測力實驗。該廊橋結構建于730 m 懸崖，呈楓葉形狀，懸挑長達29 m，結構最寬處達35 m，設計風速為32.6 m/s。以此楓葉型廊橋為背景，基于風洞實驗著重分析山區(qū)風環(huán)境下結構在各風偏角及風攻角下的靜力三分力系數(shù)。鑒于近年來此類山區(qū)觀景橋梁不斷涌現(xiàn)且其跨度不斷增大，實驗結果對山區(qū)風環(huán)境下類似長懸挑結構的靜力抗風設計具有重要的意義。

1 風洞實驗

1.1 實驗設備

實驗在成都西南交大XNJD-3 風洞進行。實驗段尺寸36 m（長）×22.5 m（寬）×4.5 m（高），風速范圍1.0～16.5 m/s，通過被動模擬裝置模擬湍流場，可實現(xiàn)《建筑結構荷載規(guī)范》中要求的各湍流場特性。實驗段地面底板裝有可自由轉動的轉盤，用以實現(xiàn)風偏角在0°～360°范圍中的轉變。如圖1 所示，實驗采用的ATI 六軸力/ 力矩傳感器Gamma 天平測量懸挑和平臺的結合處與底座和山體的結合處的基底力和力矩。該Gamma 天平采用高精度加工的高強度航空鋁型材，單軸許用荷載是額定荷載的6.9～31.6 倍。

圖1 ATI 六軸力/ 力矩傳感器Ga mma 天平

風洞中湍流場被動模擬采用尖塔、擋板、粗糙元等裝置，可準確模擬規(guī)范中各類別湍流場風速剖面、湍流強度剖面及湍流脈動風速譜等。

結合實驗中結構模型幾何尺寸和細部構造、山地地形特點以及阻塞率的實驗條件，實驗最大限度還原了橋址處地形。模型幾何縮尺比為1∶80，模型長度0.36 m，最寬處為0.43 m，阻塞率小于5%，滿足實驗要求。

1.2 實驗工況

本實驗為剛性模型實驗，在均勻流場中執(zhí)行，可以獲得該廊橋結構的三分力系數(shù)。

考慮到結構的特殊性，本次實驗主要考察懸挑和平臺的結合處與底座和山體的結合處的力學性質(zhì)，將Gamma 測力天平搭設于這兩處位置，且對此兩處位置的天平連接方式進行合理處理以實現(xiàn)實驗所需風攻角的轉變，實驗模型及天平布置如圖2 所示。

圖2 模型及測力天平設置示意圖

將山體模型固定于風洞地面底板的轉盤上，通過人工旋轉該轉盤以改變實驗風偏角，在0°～360°風偏角內(nèi)分別進行多組實驗，并在不利風偏角范圍中增加實驗工況，角度間隔取為5°，同時在較為安全風偏角范圍中適當加大實驗角度間隔。該實驗中風攻角和風偏角的設置如圖3 所示。其中風攻角包含-3°、-1°、0°、1°、3°共5 個角度，風偏角包含0°～360°內(nèi)共33 個角度。實驗工況如圖3 所示。

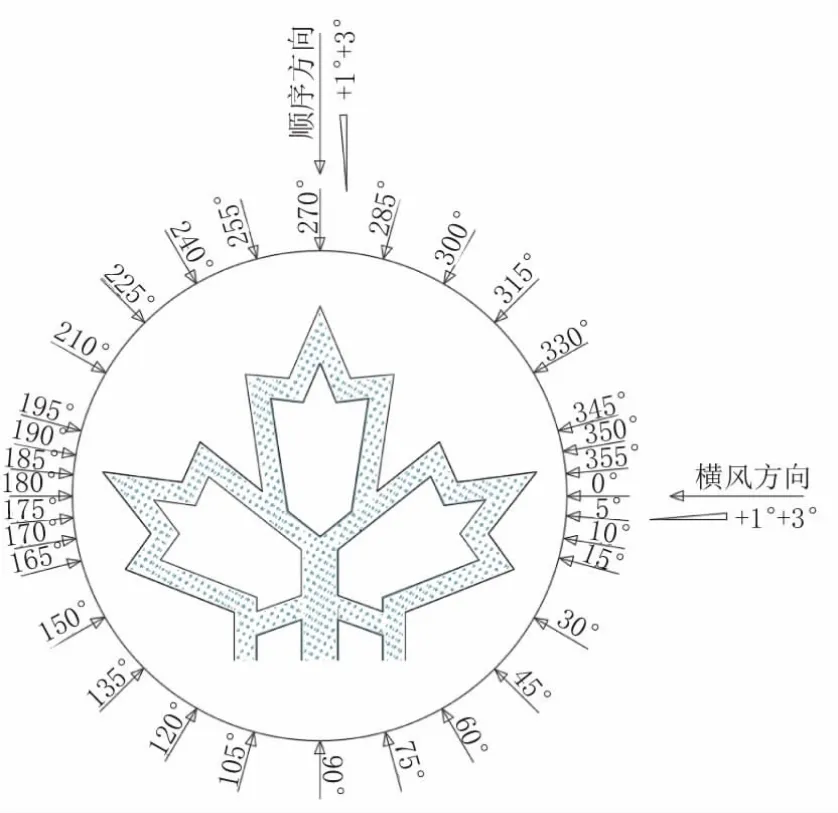
圖3 風洞實驗風偏角及風攻角示意圖

模型風洞實驗示意圖如圖4 所示。據(jù)圖4 可知，楓葉橋周圍山體雖然類似于懸崖，但存在一定起伏。在0°時，橋體被部分山體遮擋，對于來流風有一定的影響；在90°時，橋體與同一高度的山體平齊，山體從右至左逐漸下降；在180°時，橋體并未被山體遮擋，其受到的影響最小；在270°時，橋體正對來流方向，山體完全在后橋體后側。

圖4 模型風洞實驗示意圖

2 實驗結果

在速度U 為的來流風中，結構斷面將受到順橋向的力Fz和橫橋向的力Fx以及流動引起的靜力矩My，如圖5 所示，體軸坐標系中三分力系數(shù)主要是揭示結構斷面在平均風作用下受力大小的無量綱系數(shù)，反映風對結構的定常氣動力效應[10-11]。三分力系數(shù)的計算公式[12]如下：

圖5 作用在結構上的靜力三分力

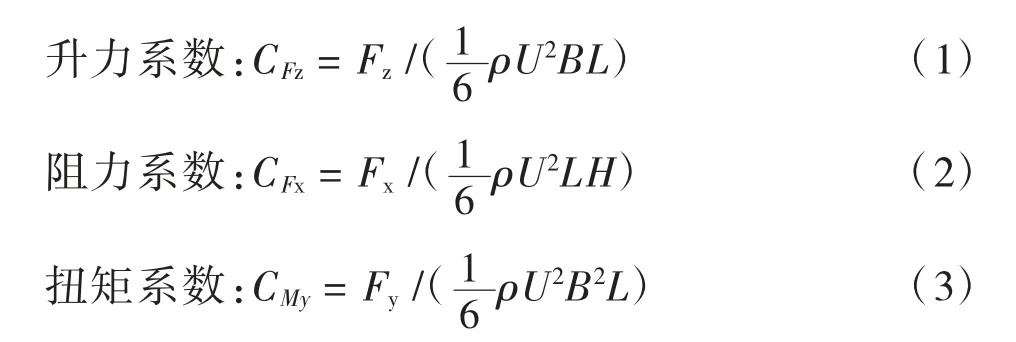
式中：CFz、CFx、CMy表示在結構體軸坐標系中的升力系、阻力、扭矩系數(shù)；Fz、Fx、My分別表示在體軸坐標系中的升力（N）、阻力（N）、扭矩（N·m）；ρ 為空氣密度（kg/m3）；U 為設計風速（m/s）；H、B、L 分別為模型的高度（m）、寬度（m）和 長度（m）（將廊橋結構順橋向定義為長度方向，橫橋向為寬度方向，本實驗采用的參考尺寸分別為0.026 m、0.43 m、0.36 m）。

根據(jù)實驗中所取得的數(shù)據(jù)，通過三分力系數(shù)公式，可以得到結構的兩處位置在體軸坐標系下的三分力系數(shù)，如圖6 所示，其中圖6（a）、圖6（b）、圖6（c）為天平位置1（懸挑和平臺的結合處）的三分力系數(shù)曲線，圖6（d）、圖6（e）、圖6（f）為天平位置2（平臺底座和山體的結合處）的三分力系數(shù)曲線。

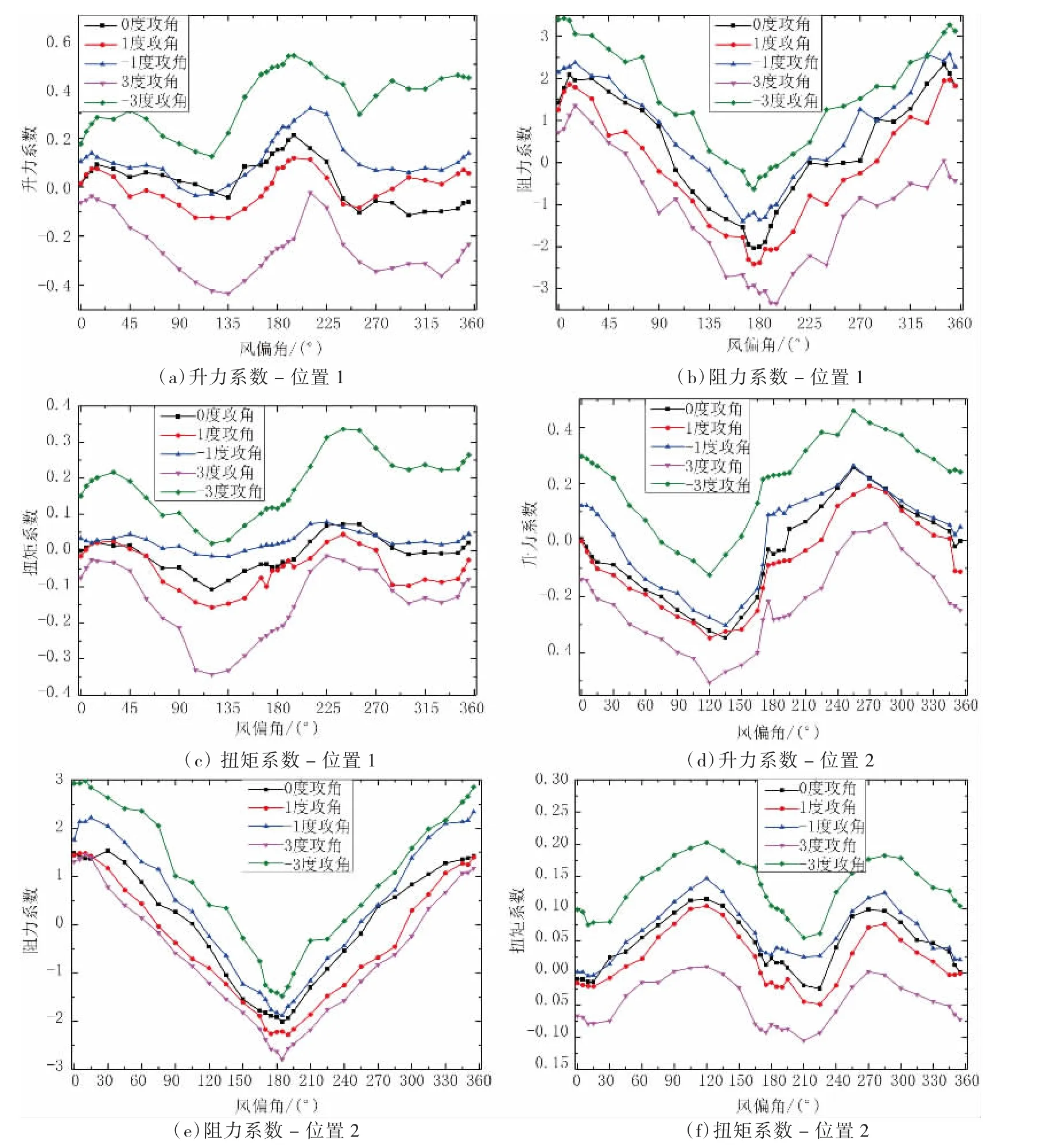
圖6 結構靜力三分力系數(shù)

3 實驗結果分析

根據(jù)三分力系數(shù)曲線可看出，山體對湍流場及三分力系數(shù)存在明顯影響。雖然隨著風偏角的變化，結構靜力三分力系數(shù)均展現(xiàn)出各不相同的規(guī)律性，但是由于場地模型的原因，在個別的風偏角下，其對應的結構三分力系數(shù)會出現(xiàn)與整體規(guī)律性不一致的突變。同時，可以看到在不同位置處的三分力系數(shù)在體軸系的同一方向上展現(xiàn)出一致的規(guī)律性。

在不同實驗風攻角下，隨風偏角的改變，結構三分力系數(shù)曲線走勢基本一致，且風攻角對三分力系數(shù)值的大小有明顯影響，風攻角越大，其偏移0°攻角的三分力系數(shù)范圍越大。

根據(jù)風洞實驗位置圖可知，橋體結構的位置是關于0°～180°和180°～360°這兩個風偏角對稱的，但由于地形不對稱因素的影響，可以看到根據(jù)實驗得到的三分力系數(shù)曲線在0°～180°和180°～360°這兩個風偏角范圍中并未呈現(xiàn)嚴格的對稱。

3.1 懸挑與平臺結合處

對于懸挑和平臺結合處，其升力系數(shù)大體呈現(xiàn)出單邊增大→減小→增大的對稱的趨勢，當風攻角為-3°，風偏角在210°附近時出現(xiàn)最大值0.536，當風攻角為3°，風偏角在135°和330°附近出現(xiàn)最小值-0.434；阻力系數(shù)曲線大體上呈現(xiàn)減小→增大的趨勢，當風攻角為3°，風偏角在180°附近時出現(xiàn)最小值-3.350，當風攻角為-3°，風偏角在5°和355°附近時出現(xiàn)最大值3.43；對于扭矩系數(shù)，當風攻角為3°，風偏角在120°附近出現(xiàn)最小值-0.343，當風攻角為-3°，風偏角在240°附近時出現(xiàn)最大值0.336。

升力系數(shù)曲線在風偏角從0°、360°向180°靠攏的過程中，其呈現(xiàn)出增大→減小→增大的走勢，考慮到山體地形形狀的因素，這是由崖壁對來流風的阻擋使得風的回流不斷增大，風沿崖壁向上折向橋體的回流致使結構升力系數(shù)增大。因此，考慮當?shù)斤L偏角在180°～270°范圍內(nèi)時，來流風被下部山體阻擋后沿著崖壁向上折向結構，造成升力系數(shù)增大，使得其最大值出現(xiàn)在210°風偏角附近。

阻力系數(shù)曲線呈現(xiàn)出減小→增大的走勢，不同攻角下阻力系數(shù)最大值均在15°和345°風偏角附近出現(xiàn)，根據(jù)測力天平位置可以得出，結構受到的阻力為橫橋向，隨風偏角的變化，來流方向與橫橋向之間的夾角逐漸變化，至90°和270°時，夾角達到最小值，阻力系數(shù)在90°、270°附近趨近于0°。在風偏角為0°及180°時，夾角達到最大值，但因山體地形的影響，阻力系數(shù)在15°和345°風偏角附近出現(xiàn)極大值，185°附近出現(xiàn)極小值。

扭矩系數(shù)曲線呈現(xiàn)出規(guī)律性的增大→減小→增大的反對稱的趨勢，在30°、240°附近出現(xiàn)極大值，在120°、330°附近出現(xiàn)極小值，同時隨著攻角的增大，其均方根也隨之增大。

3.2 平臺底座與山體結合處

對于平臺底座和山體結合處，其升力系數(shù)大體呈現(xiàn)單邊減小→增大的反對稱的趨勢，當風攻角為-3°，風偏角在255°附近時出現(xiàn)最大值0.458，當風攻角為3°，風偏角在120°附近時出現(xiàn)最小值-0.506；阻力系數(shù)曲線大體上呈現(xiàn)減小→增大的趨勢，當風攻角為3°，風偏角在180°附近出現(xiàn)最小值-2.793，當風攻角為-3°，風偏角在5°和355°附近時出現(xiàn)最大值2.929；對于扭矩系數(shù)，當風攻角為3°，風偏角在210°附近出現(xiàn)最小值-0.105，當風攻角為-3°，風偏角在120°和285°附近出現(xiàn)最大值0.203。

升力系數(shù)曲線在風偏角變化過程中，可看到其呈現(xiàn)出明顯的變化規(guī)律：減小→增大→減小。根據(jù)此處升力在體軸中的方向，考慮山體地形的影響，其在135°附近出現(xiàn)極小值，在正對來流方向，即風偏角270°附近出現(xiàn)極大值，同時由于山體的遮擋，可以發(fā)現(xiàn)升力在165°風偏角附近表現(xiàn)出明顯的上升變化。

4 結語

本文通過剛性模型風洞實驗對結構靜力三分力系數(shù)研究分析，可得出以下結論：

（1）隨著來流風偏角的變化，靜力三分力系數(shù)呈現(xiàn)出規(guī)律性的變化趨勢，山體地形對三分力系數(shù)的影響顯著。

（2）結構三分力系數(shù)隨風攻角的改變而變化，并且風攻角越大，其對應的結構三分力系數(shù)值也越大。

（3）對于結構不同位置處的三分力系數(shù)，在結構體軸系上的相同方向，其數(shù)值隨著風偏角的變化，表現(xiàn)出了一致的變化趨勢。

（4）因山體地形及結構外形的綜合影響，當風偏角在135°、210°和330°附近時，升力系數(shù)易出現(xiàn)極值；當風偏角在5°、180°和355°附近時，阻力系數(shù)易出現(xiàn)極值；當風偏角在120°和240°時，扭矩系數(shù)易出現(xiàn)極值，結構設計中應加以重視。