系梁對啞鈴型承臺基礎承載特性的影響研究

黃 潔

[上海市政設計研究總院（集團）有限公司，上海市200092]

0 引言

隨著交通流量的逐年增加，我國新建及擬建橋梁結構的橋面寬度逐漸加大。因此，橋梁基礎承臺的平面尺寸逐漸增大。為了保證承臺與樁基之間的相對剛度，減小承臺自身的重量，分離式的啞鈴型承臺逐漸成為目前大跨橋梁結構基礎常采用的一種形式。與整體式承臺不同，分離式的啞鈴型承臺是由兩個獨立的承臺之間通過一根系梁連接而成。國內外學者也對啞鈴型承臺基礎的受力性能進行了一定的研究。目前，系梁剛度及樁基布置對啞鈴型承臺基礎承載變形特性的影響研究不多。

在目前的實際工程中，承臺系梁一般采用鋼筋混凝土材料。系梁的截面尺寸如何設計對啞鈴型承臺基礎受力更有利，系梁底布置樁基是否合適等問題并沒有得到論證。因此，現將結合有限元方法、橋梁結構理論[1]及公路橋梁規范[2-3]，對上述問題進行研究，以期對啞鈴型承臺的設計和使用提供指導。

1 啞鈴型承臺群樁基礎計算模型

現以一實際橋梁工程的啞鈴型承臺基礎為背景，建立有限元分析模型。該橋主橋上部結構為漂浮體系斜拉橋。主墩承臺為啞鈴型承臺，主墩每側啞鈴型部分半徑18.7 m，其下布置28 根2500 mm 鉆孔灌注樁，樁長79 m，沖刷線以上樁長9.2 m。承臺圓柱形部分高11 m，園錐形部分高5 m。

現結合有限元法，使用MIDAS FEA 軟件進行建模。橋墩和承臺系梁采用有限元實體單元模擬，樁基采用梁單元模擬，轉換模型重量為集中質量。承臺與墩底、系梁和樁頂剛性連接，樁底固結。上部結構作用于橋墩頂部，上部結構傳遞的單個墩柱主要荷載如表1 所列，其中汽車荷載與上部結構恒載為對稱荷載，橫向風荷載為反對稱荷載；分析模型如圖1 所示。

表1 FEA 計算荷載匯總表（單個墩柱）

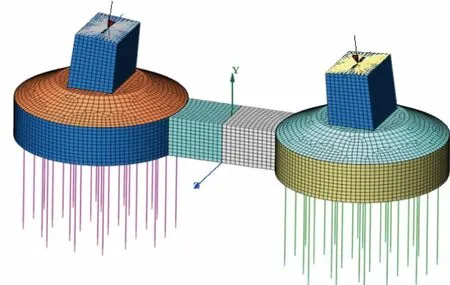
圖1 啞鈴型承臺基礎有限元模型

2 不同寬度系梁對啞鈴型承臺群樁基礎承載特性的影響

2.1 不同寬度系梁對系梁自身的內力影響

現建立不同寬度（B=12、16、20 m）系梁的有限元模型，系梁高H=11 m，分析不同寬度系梁在各類型荷載作用下對系梁中點內力的影響。系梁中點內力反應出系梁傳遞承臺間的內力，同時也控制著系梁本身結構承載力驗算。

表2～表5 分別為啞鈴型承臺在自重作用、上部結構恒載、橫向風荷載作用下，以及汽車荷載作用下系梁中點內力對比表。從表中可以看出，除了在橫向風作用下系梁中點內力幾乎為零。系梁寬度越寬，系梁抗彎剛度則越大。系梁寬度B=20 m 比系梁寬度B=12 m 的抗彎剛度增加66%，在自重作用下，系梁中點產生了很大的軸力，以及彎矩，軸力增加54.9%，彎矩增加112%。在橫向風作用、上部結構恒載，以及汽車荷載作用下，隨著系梁的增寬，系梁傳遞的軸力沒有變化，彎矩分別增加了39.79%、35%，以及37.31%。

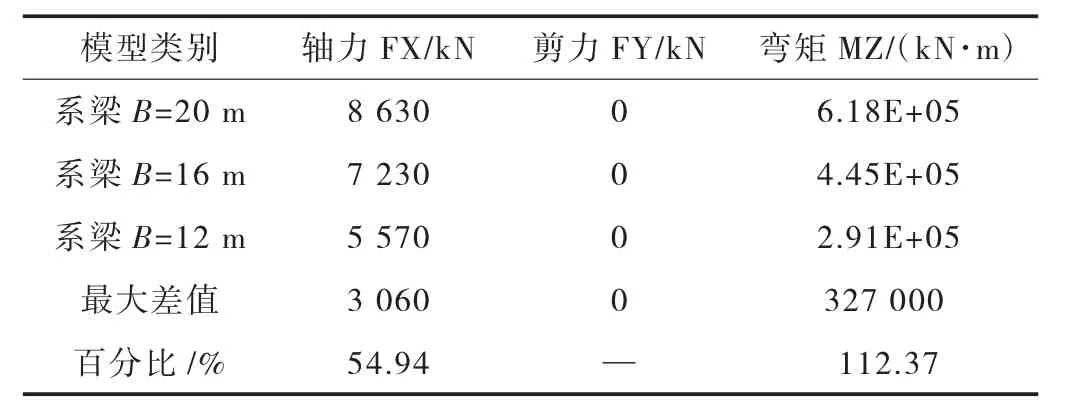
表2 自重作用下不同寬度系梁中點內力表

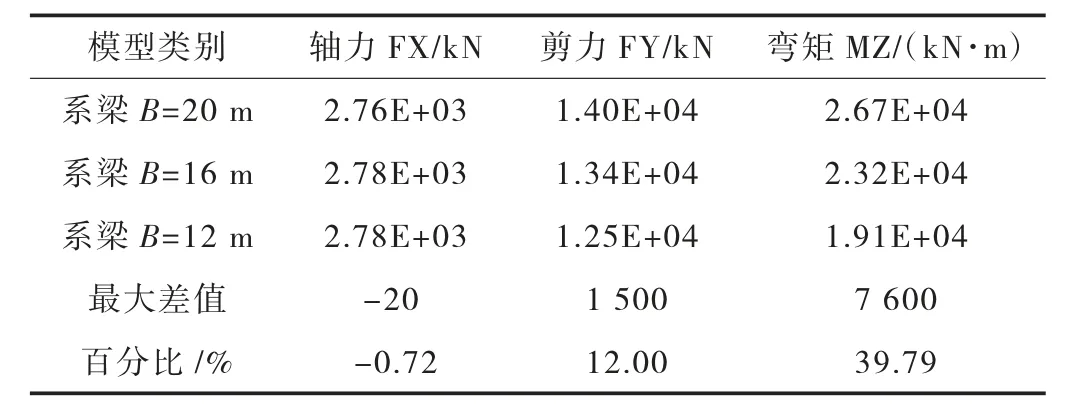
表3 橫向風荷載作用下不同寬度系梁中點內力表

表4 上部結構恒載作用下不同寬度系梁中點內力

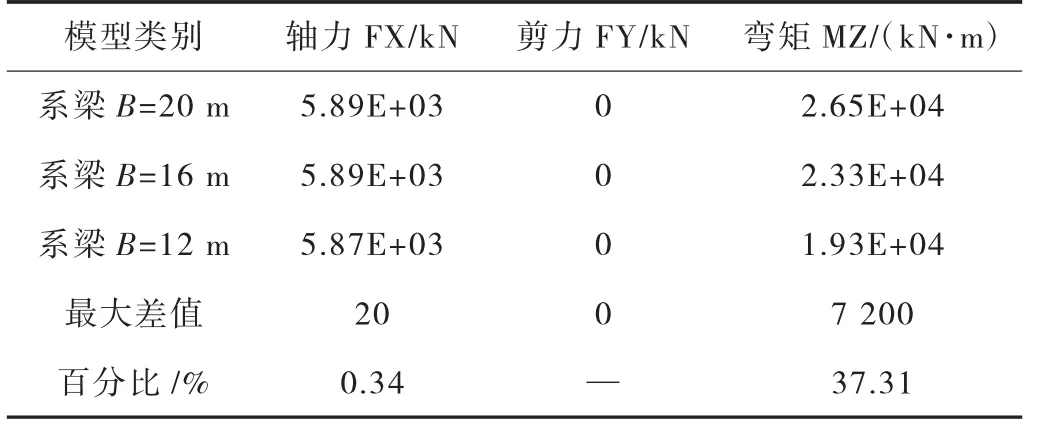
表5 汽車作用下不同寬度系梁中點內力

綜上所述，系梁寬度影響著系梁剛度，系梁剛度影響了系梁在承臺間傳遞的剪力與彎矩，但對系梁在承臺間傳遞的軸力影響很小。

系梁在自重作用時，主要向承臺傳遞系梁自身重力，隨著系梁寬度增加，自身重力的增量及百分比都很大，對結構不利；在橫向風荷載、上部結構恒載，以及汽車荷載作用下，隨著系梁寬度增加，剛度增大，傳遞的剪力或彎矩有較大增加，對結構有利。自重作用下增加的對承臺不利彎矩，要明顯大于其他荷載作用下對承臺傳遞的有利彎矩。

2.2 不同寬度系梁對樁頂反力分布的影響

在上述不同寬度（B=12、16、20 m）系梁的有限元對比模型的基礎上，分析不同系梁寬度對啞鈴型承臺群樁基礎樁頂反力分布的影響。

表6～表9 分別為啞鈴型承臺自重作用、橫向風荷載作用、上部結構恒載及汽車荷載作用下樁頂反力對比表。從表中可以看出，隨著系梁寬度增加，自重作用下樁頂最大軸力及最大彎矩都增加，對樁基結構受力不利。其他上部結構荷載作用下，隨著系梁寬度增加，樁頂最大軸力及彎矩都有所減小。其中，由于在橫向風作用下，系梁傳遞剪力，所以最大軸力減小的幅度最大。

表6 自重作用下樁頂反力表

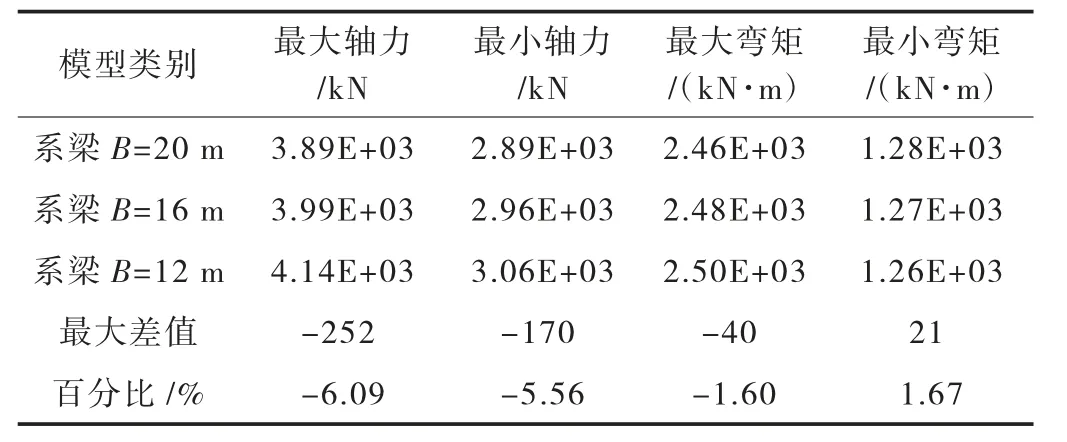
表7 橫向風荷載作用下樁頂反力

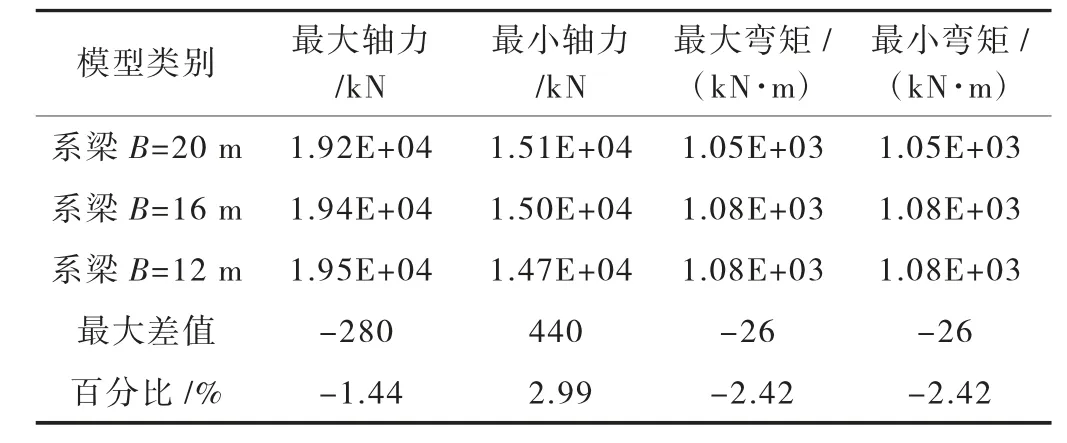
表8 上部結構恒載作用下樁頂反力

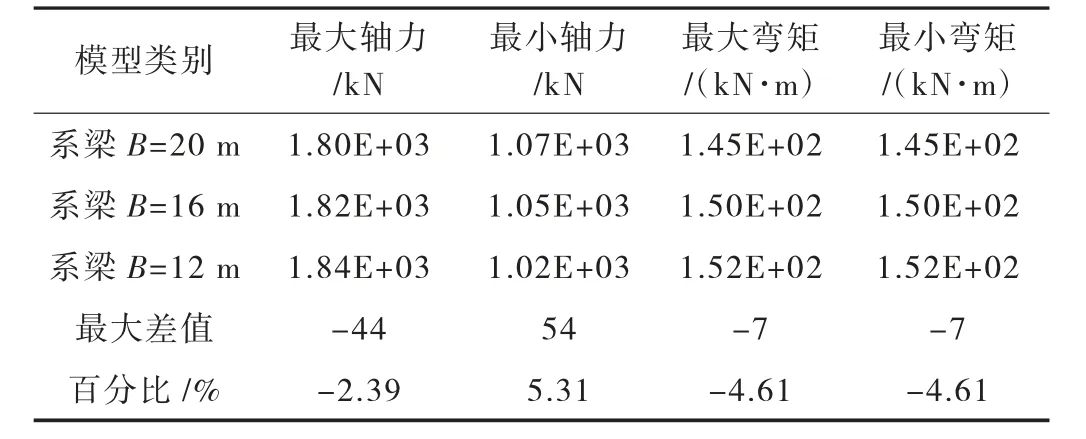
表9 縱向汽車荷載作用下樁頂反力

啞鈴型承臺隨著系梁寬度增加，系梁自重增加，向承臺傳遞很大的內力，從而導致樁頂反力增加很大。在其他荷載作用下，系梁向承臺間傳遞的軸力變化百分比很小，傳遞的彎矩有所增加，但彎矩一般均分至承臺底的眾多樁頂上，從而導致樁頂最大軸力及彎矩有所增加，但增加百分比很小。

3 不同高度系梁對啞鈴型承臺群樁基礎承載特性的影響

3.1 不同高度系梁對系梁自身的內力影響

建立了對比有限元模型，其系梁取不同高度H=11 m 及H=7 m，系梁寬度取B=12 m，對比分析系梁高度在各類型荷載作用下對系梁中點內力的影響。系梁中點內力反應出系梁傳遞承臺間的內力，同時也控制著系梁本身結構的承載力。

表10 為啞鈴型承臺在自重作用下系梁中點內力對比表。系梁高度越高，系梁抗彎剛度則越大。系梁高度H=7 m 比系梁寬度H=11 m 的抗彎剛度減小了74.2%，在自重作用下，系梁中點軸力減小16.52%，彎矩減小65.84%。同時通過研究表明：在橫向風作用、上部結構恒載，以及汽車荷載作用下，隨著高度的減小，系梁傳遞的軸力變化百分比很小，彎矩分別減小了67.64%、70.79%及69.53%。在橫向風作用下，系梁傳遞的剪力減小了27.8%。

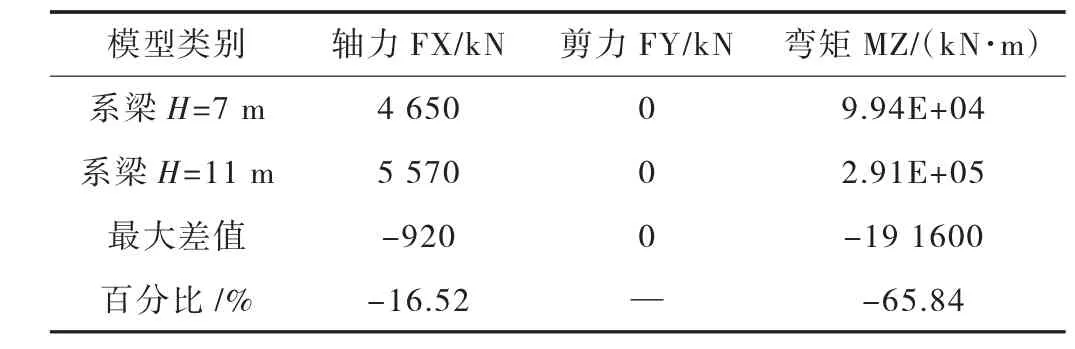
表10 自重作用下不同高度系梁中點內力對比表

綜上所述，由于系梁高度比寬度對系梁剛度的影響更大，系梁增加高度比系梁增加寬度，在系梁自重作用下對承臺不利影響更小；在其他荷載作用下，系梁傳遞的彎矩增加百分比也更大，對結構的有力影響也更大。不同高度系梁在其他荷載作用下在承臺間傳遞的軸力相近。

3.2 不同高度系梁對樁頂反力的影響

在上述不同高度的有限元對比模型的基礎上繼續分析系梁高度在各荷載類型作用下對樁頂反力的影響。

表11 為啞鈴型承臺自重作用下樁頂反力對比表。從表中可以看出，隨著系梁高度減小，自重作用下樁頂最大軸力及最大彎矩都減小，對樁基結構受力有利。同時通過研究表明，在橫向風荷載作用下，由于系梁傳遞剪力及彎矩，承臺底樁基最大軸力增加12.71%，對樁基結構不利。在上部結構恒載及汽車荷載作用下，樁頂反力變化不大。

表11 自重作用下樁頂反力對比表

綜上所述，系梁高度主要影響系梁剛度，系梁剛度影響了系梁在承臺間傳遞的剪力與彎矩，但對系梁在承臺間傳遞的軸力影響較小。

隨著啞鈴型承臺系梁高度減小，自重減小對樁基的有利影響要遠遠大于橫向風作用下對樁基的不利影響。

4 系梁樁基對啞鈴型承臺群樁基礎承載特性的影響

在工程實踐中，啞鈴型承臺往往在系梁底設置樁基。現通過分析系梁下樁基是否影響承臺整體的抗彎剛度，進而對啞鈴型承臺的基礎承載特性產生影響，從而建立MIDAS FEA 有限元模型對比模型，分析系梁底樁基的作用，其中系梁寬度B=12 m，高度H=11 m，樁基距對稱中心線8.0 m（見圖2）。圖3、圖4 為系梁下無樁（或有樁）在自重作用及上部恒載作用下樁頂軸力圖。

圖2 系梁下有樁啞鈴型基礎FEA 有限元模型

由圖3 及圖4 可以看出，在系梁自重及上部結構恒載作用下，系梁下設置樁基，其樁底最大軸力只減小0.017%。這是由于在自重作用下，系梁下樁基主要承受系梁的自重作用，承臺內側樁頂反力得以大幅度降低；在上部結構恒載作用下，由于系梁下樁基增加了承臺間的系梁的剛度，啞鈴型承臺最外側樁基承擔的樁頂反力更大。

圖3 系梁下無樁在自重作用及上部恒載作用下樁頂軸力圖（單位：kN）

圖4 系梁下有樁在自重作用及上部恒載作用下樁頂軸力圖（單位：kN）

同時，由圖3、圖4 可看出，在自重及上部結構恒載作用下，系梁下設置樁基時，啞鈴型承臺下樁基反力相差很大，樁頂軸力相差24.8%，樁基承載力利用率不高。

另外通過研究表明，在橫向風荷載及縱向汽車荷載作用下，啞鈴型承臺最不利樁頂反力的位置也為承臺最外兩側，且在橫向風荷載及縱向汽車荷載作用下，樁頂反力變化差值很小。

在此工程實例中，在橋梁結構上下部恒載作用下，系梁底設置樁基對整個承臺的最大樁頂反力影響有限；同時，系梁底樁基受力較小，其樁基承載力不能得到充分利用。所以得出結論，在系梁自身承載力驗算得到滿足的情況下，不需要設置系梁底樁基。

5 結論

以一座下部結構為啞鈴型承臺的漂浮體系斜拉橋工程為背景，提取上部結構主要荷載，建立有限元分析模型，主要研究系梁對啞鈴型承臺結構特性的影響，得出以下結論:

啞鈴型承臺基礎的系梁越寬或越高，系梁的剛度越大，在上部結構主要荷載作用下傳遞的軸力變化很小，傳遞的彎矩更大，在橫向風作用下能傳遞更大的剪力，對承臺結構的樁基反力有利。

啞鈴型承臺基礎的系梁越寬或越高，系梁自重越大，向承臺傳遞很大的剪力和彎矩，對承臺結構的樁基反力更為不利。系梁自重增大的不利影響要遠遠大于剛度增加的有利影響

啞鈴型承臺系梁底樁基主要承擔系梁的自重，系梁底樁基對整個承臺的最大樁頂反力影響有限。同時，系梁底樁基受力較小，其樁基承載力不能得到充分利用。

綜上所述，啞鈴型承臺的系梁的主要作用應為傳遞承臺間軸力，而非承擔剪力和彎矩。因此，系梁本身不需要過大的剛度。系梁的寬度及高度不必過大，從而簡化基礎受力途徑，減小系梁自重，提高基礎承載力特性，提高啞鈴型基礎經濟性。