Q-m-clean環(huán)及其推廣

李 瑩， 殷曉斌

(安徽師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院，安徽 蕪湖 241000)

1 引言與預(yù)備知識

本文中的環(huán)都是指含單位元的結(jié)合環(huán)。E(R)，U(R)分別表示環(huán)R中的冪等元和可逆元之集。

1977年Nicholson W K在文獻[1]中研究exchange環(huán)時提出clean環(huán)的概念。若環(huán)R中的每個元素都可以表示成一個冪等元和一個可逆元之和，則稱R是clean環(huán)。隨后很多學(xué)者對clean環(huán)做了更進一步的研究。

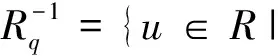
在文獻[2]中Ara P還定義了(Neumann)等價關(guān)系。設(shè)R是環(huán)，p,q∈E(R)，若存在u,v∈R使得1-p=uv，1-q=vu，則稱1-p與1-q是(Neumann)等價的，記作1-p～1-q。

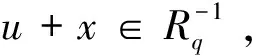
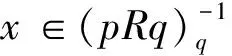
引理1.3[3]設(shè)R是環(huán)，元素p,q∈E(R)，且1-p～1-q，即存在u,v∈R使得1-p=uv，1-q=vu。如果u+x在R里是左可逆或右可逆的，那么對于任意的形式為u+x+(1-p)yq的元素也有相同的性質(zhì)。

2019年，Purkait S等在文獻[4]中給出了m-clean環(huán)的概念。若環(huán)R中的每一個元素都可以寫成一個m-potent元與可逆元之和的形式，則稱環(huán)R是m-clean環(huán)。若環(huán)R中的元素f滿足條件fm=f，則稱f是R中的m-potent元。本文中的m都是大于等于2的正整數(shù)。

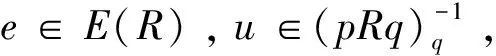
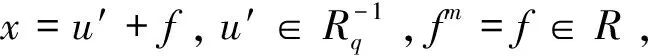
2 主要結(jié)論

定義2.1設(shè)R是一個環(huán)，若R中的一個元素x可以寫成x=u+f的形式，其中u是R中的擬可逆元，f是R中的m-potent元，則稱x為環(huán)R中的Q-m-clean元。如果R中的每個元素都是Q-m-clean元，則稱R是Q-m-clean環(huán)。進一步，若uf=fu，則稱x是強Q-m-clean元。如果環(huán)R中的每個元素都是強Q-m-clean元,則稱環(huán)R是強Q-m-clean環(huán)。

引理2.2由于E(R)都是m-potent元，根據(jù)定義我們有下面的結(jié)論成立。

(1)每個m-clean環(huán)是Q-m-clean環(huán)。

(2)每個Q-clean環(huán)是Q-m-clean環(huán)。

推論2.3如果環(huán)R中每個元素都是m-potent元，則R是Q-m-clean環(huán)。

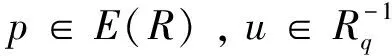
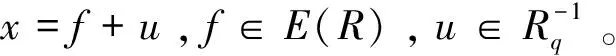
px=p(f+u)=pu，(p-1)(x-1)=(p-1)u。

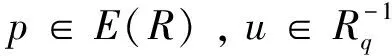
pu-u=(p-1)(x-1)=px-p-x+1。

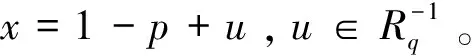
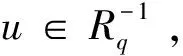
證明由f是R中的m-potent元可知fm-1是R中的冪等元，再由引理2.4即得證。

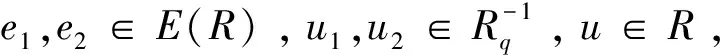
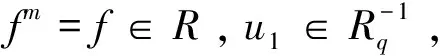
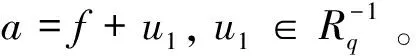
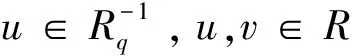
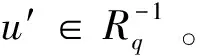
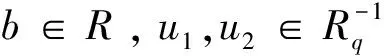
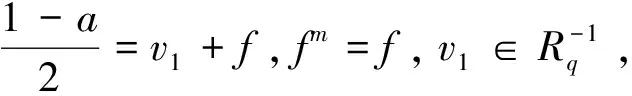
命題2.9設(shè)R是一個環(huán)，e∈E(R)，a∈eRe。若a是eRe中的Q-m-clean元，則a是環(huán)R中的Q-m-clean元。

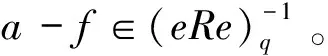
推論2.10設(shè)R是環(huán)，e∈E(R)，a∈eRe。若a是eRe中的Q-m-clean元，則對任意的c∈(1-e)Re，a+c是環(huán)R中的Q-m-clean元。

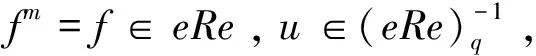
引理2.11設(shè)R是環(huán)，u,v∈R，p,q∈E(R)，且1-p=uv，1-q=vu。若x∈pRq是pRq中的Q-m-clean元，則u+x是R中的Q-m-clean元。

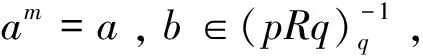
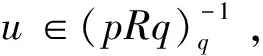
推論2.13設(shè)R是環(huán)，u,v∈R，p,q∈E(R)，且1-p=uv，1-q=vu。若pRq是Q-m-cleancorner，則u+pRq中的每一個元素均為Q-m-clean元。

推論2.14設(shè)R是環(huán)，0≠p∈E(R)。若pRq是R的Q-m-cleancorner，則1-p+pRq中的每一個元素均為Q-m-clean元。

引理2.15設(shè)R是環(huán)，e∈E(R)。如果eRe和(1-e)R(1-e)都是R的Q-m-cleancorner，則環(huán)R中的每個元素都可以寫成兩個Q-m-clean元之和。

證明設(shè)R=eRe+eR(1-e)+(1-e)Re+(1-e)R(1-e)為R的Pierce分解。則對任意r∈R，r=a+b+c+d，其中a∈eRe，b∈eR(1-e)，c∈(1-e)Re，d∈(1-e)R(1-e)。由推論2.10可得a+c，b+d是R中的Q-m-clean元。

引理2.16設(shè)R是環(huán)，e是R中的m-potent元。若em-1Rem-1是R的Q-m-cleancorner且(1-em-1)R(1-em-1)是clean環(huán)，則R是Q-m-clean環(huán)。

證明由e是m-potent元，可得em-1是冪等元。再由[3,定理2.5]的證明可得結(jié)論。

定義2.17[6]設(shè)R是環(huán)，如果環(huán)R中的冪等元均為中心冪等元，則稱環(huán)R是Abel環(huán)。

命題2.18設(shè)R是Abel環(huán)，e∈E(R)。則eRe和(1-e)R(1-e)都是R的Q-m-cleancorner當(dāng)且僅當(dāng)R是Q-m-clean環(huán)。

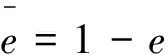
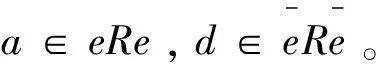
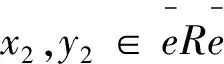
于是

(1-(u1+u2)(x1+x2))r(1-(y1+y2)(u1+u2))

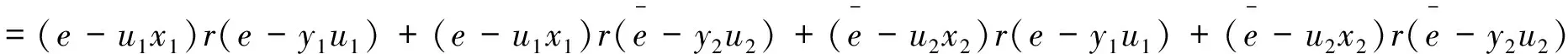
=0+0+0+0=0。

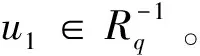
推論2.19若R是Abel環(huán)，則下列條件等價：

(1)R是Q-m-clean環(huán)；

(2)存在完全正交的冪等元集{e1,e2,…en}使得eiRei(i=1,2,…,n)(n≥2)都是環(huán)R的Q-m-cleancorner。

證明(1)?(2)由命題2.18易得。

(2)?(1)，對n用歸納法。

當(dāng)n=2時，1=e1+e2，由命題2.18，(1)顯然成立。

若(1)對n-1成立，即1=e1+e2+…+en-1，且每個eiRei(i=1,2,…n-1)是Q-m

cleancorner時，可得R是Q-m-clean環(huán)。下證結(jié)論(1)對n成立:若1=e1+e2+…+en

則1=e1+e2+…+(en-1+en)，(en-1+en)ei=0(i=1,2,…n-2)，(en-1+en)2=en-1+en。于是存在完全正交的冪等元集{e1,e2,…et}，其中et=en-1+en，且e1,e2,…et是n-1個冪等元，則容易得到R是Q-m-clean環(huán)。于是(1)對任意n均成立。

推論2.20設(shè)R是Abel環(huán)且e∈E(R)。若a是R中的Q-m-clean元，則ae是R中的Q-m-clean元。

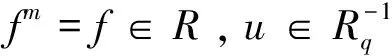
定義2.21[7]設(shè)R是一個環(huán)，若對任意的a∈R，存在x∈R使得axa=a，則稱R是正則環(huán)。

推論2.22設(shè)R是正則環(huán)，且a∈R。若EndR(aR)是Q-m-clean環(huán)，則元素a是R中的Q-m-clean元。

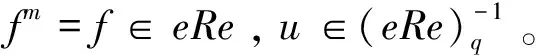
a=ae+a(1-e)=(f+1-e)+u-1+e+a(1-e)。

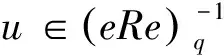
(e-uv)+(u-1+e+a(1-e))(v-1+e)=1-a(1-e)。

于是有

(e-uv)(1+a(1-e))+(u-1+e+a(1-e))(v-1+e)(1+a(1-e))=1。

從而

1-(u-1+e+a(1-e))(v-1+e)(1+a(1-e))=(e-uv)(1+a(1-e))。

同理有

1-(1+va(1-e))(v-1+e)(u-1+e+a(1-e))=(1+va(1-e))(e-uv)。

因此

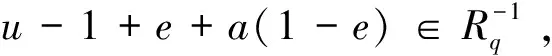
命題2.23根據(jù)Q-m-clean環(huán)的定義我們有下面的結(jié)論成立。

(1)Q-m-clean環(huán)的每個同態(tài)像是Q-m-clean環(huán)。

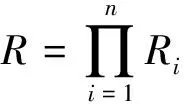
證明(1)和(2)的必要性是顯然的,下證(2)的充分性。