基于循環神經網絡的一種在線輔助CVT電壓誤差測量方法

陳文中， 陳俊杰， 許 侃， 張金麗

(國家電網上海市電力公司電力科學研究院， 上海 200437)

隨著科技水平的提高，我國配電網絡的覆蓋范圍越來越廣，電力用戶的規模也越來越龐大，同時電能計價的細微變化會直接影響大量電力用戶的日常生活，因此電能計價的公平性必須得到充分的保障，這對國計民生和國民經濟的穩固發展都有著重要的影響。保證電能計價公平性的前提是對電力系統中的電壓和電流大小進行精確測量。電容式電壓互感器(capacitor voltage transformer，CVT)[1-2]常被廣泛應用于100 kV及以上電壓等級的電力系統中，以實現一次電壓、電流的精確測量。CVT雖然具有絕緣性能好、經濟性高等優點，但相比傳統的電磁式電壓傳感器，CVT的電路結構較為復雜，容易受到周圍自然環境、電場等外界因素的影響，使其測量穩定性降低。CVT的測量穩定性直接關系到電能計價的公平性。因此，如何準確地評估CVT的計量誤差成了很多研究者的研究重點。昌云松等[3]提出一種基于滑動窗口原理和主成分分析的WMPCA(weighted multi-linear principal component analysis)誤差評估方法，相比傳統的CVT誤差評估方法，該方法準確度更高且能夠用于評估長期運行的CVT。李朝陽等[4]提出基于多元分析的互感器故障判別算法，該算法能夠在不增加額外測量設備的情況下，正確識別出存在故障的互感器。張秋雁等[5]利用前饋神經網絡建立數字電量計量系統的數字模型，從而達到正確評估系統誤差的目的。但上述文獻中提到的評估方法需要用到大量、多維度的離線數據，且需要花費大量的時間進行數據的預處理。

因此，本文提出一種基于RNN(recurrent neural network)[6]的在線輔助CVT電壓測量方法，該方法通過收集電力系統中電壓的歷史數據，利用RNN對電壓值的變化趨勢進行擬合和建模。完成RNN模型訓練之后，把當前時刻和過去幾個時刻的電壓值作為RNN的輸入值，以在線預測未來某個時刻的電壓值。將RNN的輸出值作為標準值并與CVT的實際測量數值進行誤差對比，對CVT的測量穩定性進行評估，從而幫助測量人員及時發現異常的測量值并更換CVT設備，保障電能計價的公平性。該方法不需要使用海量、多維度的離線數據，能夠利用RNN對CVT的實際測試值進行誤差評估。

1 模型與問題建立

基于RNN的在線輔助CVT電壓測量方法的主要流程如圖1所示。首先，需要收集以往電力系統中的電壓序列作為數據集，將電壓序列表示為V=(v1,v2, …,vn)，n表示總的序列長度，然后使用數據集來訓練RNN模型。簡單來講，訓練RNN模型的過程，即利用反向傳播算法和梯度下降算法來不斷地迭代更新RNN網絡中的權重系數，最終使得損失函數達到最小值。常用的梯度下降算法包括隨機梯度下降算法(SGD)[7]和Adam梯度下降算法[8]等。最后，利用訓練好的RNN模型來實時地預測下一時刻的電壓值，并與CVT得到的實測數據進行對比。訓練好的RNN模型如式(1)所示。

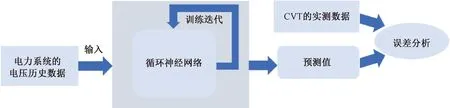
圖1 基于RNN的在線輔助CVT電壓誤差測量方法的示意圖

(1)

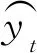
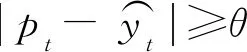
2 算法設計

2.1 RNN的網絡結構

RNN是在神經網絡的基礎上進行拓展得到的。神經網絡具有逼近任意一個函數的特點，因此該算法被廣泛應用在生物、醫療、計算機、通信等多個領域[9-10]。神經網絡的核心算法是向量乘法，并通過引入激活函數[11]來增加其擬合非線性函數的能力。

電力系統中的電壓值隨時間的變化趨勢可以看作是一個時間序列[12]，即當前時刻的電壓值和前一時刻(或前幾個時刻)的電壓值存在著某種函數映射關系。因此，選擇神經網絡來逼近這一映射關系。但由于在傳統的BP神經網絡[13]或者卷積神經網絡[14](convolutional neural network,CNN)中，當前時刻的輸入值與上一時刻的輸入值是相互獨立的，因此這兩者都不適合用來對時間序列進行建模。而RNN很好地彌補了BP神經網絡和CNN沒有“記憶能力”的缺點。

RNN簡易的示意圖如圖2所示。由圖2可知，RNN除了包含輸入層、隱藏層和輸出層以外，多了一個循環層，便于完成“記憶”的功能。

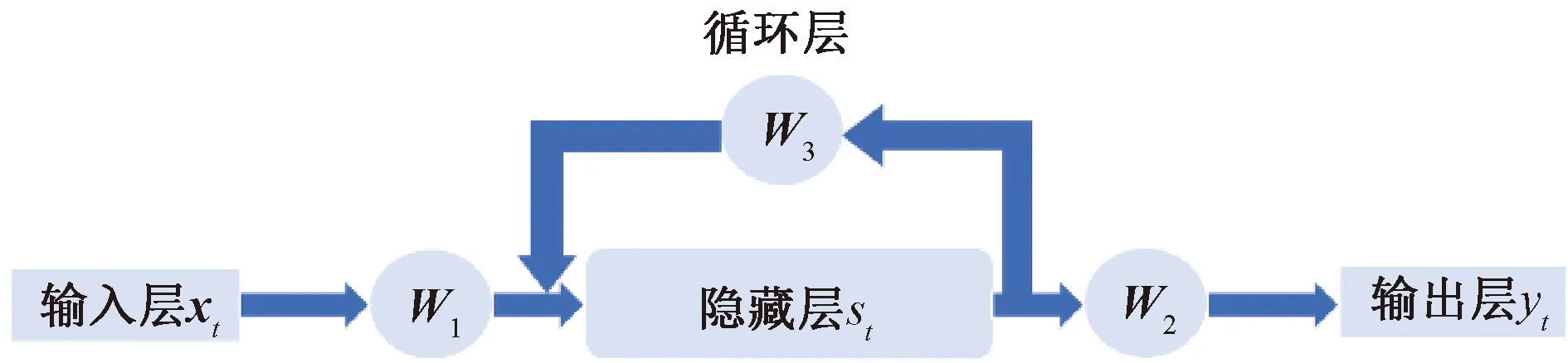
圖2 RNN的結構示意圖

其中:xt為RNN的輸入向量(下標t表示當前時刻)，其長度等于輸入數據的維度;yt為RNN的輸出向量;W1為輸入層到隱藏層這兩者之間的權重系數矩陣;st為隱藏層的值，其長度等于隱藏層神經元的個數;W2為隱藏層到輸出層這兩者之間的權重系數矩陣;W3為前一時刻的隱藏層st-1作為當前時刻的輸入信息時，要相乘的權重系數矩陣;yt和st分別如式(3)和(4)所示。

yt=g(st·W2)

(3)

st=h(xt·W1+W3·st-1)

(4)

式中：g(·)和h(·)是激活函數，能夠讓RNN更好地擬合非線性函數。

從式(4)中可以看到，隱藏層st不僅與當前時刻的輸入值xt有關，也取決于上一時刻的隱藏層st-1。接著，把式(4)不斷地代入式(3)中，可得

yt=g(h(xt·W1+W3·st-1)·W2)

(5)

yt=g(h(xt·W1+W3·h(xt-1·W1+W3·st-2))·W2)

(6)

yt=g(h(xt·W1+W3·h(xt-1·W1+W3·h(xt-2·W1+…)))·W2)

(7)

輸出層的值yt與當前時刻的輸入值xt，以及過去時刻的輸入值xt-1、xt-2、…都有一定的關系。式(5)非常直觀地體現了RNN具有“記憶”功能這一特點。

2.2 訓練RNN模型

首先，在使用電壓序列訓練RNN之前，需要對其進行數據清洗、歸一化等預處理操作，對電壓序列進行歸一化的主要目的是為了讓RNN模型更快地收斂。歸一化的具體方式可由式(8)表示。

(8)

式中：vi為某一時刻的電壓值；vmax為電壓序列中的最大值；vmin為電壓序列中的最小值；v′為歸一化后的值。

接著，需要從經過歸一化的電壓序列中生成訓練RNN所需的數據集。數據集中包含多行數據，每行數據由輸入值和對應的標簽兩部分組成。把每3個連續的序列值作為一行數據，其中(vi-2,vi-1)作為輸入值，vi則作為對應的標簽，下標i滿足2≤i≤n。得到的數據集需要進一步分成訓練集和測試集：訓練集用于訓練RNN，測試集用于評估RNN的性能好壞。然后，把RNN輸出層的預測值與標簽值的均方誤差作為損失函數來訓練RNN。RNN損失函數如式(9)所示。

(9)

式中：L代表損失函數，w表示RNN中所有的權重參數；yi表示第i條數據經過RNN后得到的預測值；K表示訓練集中樣本的個數。隨后，利用梯度下降算法不斷更新RNN網絡的權重系數以使損失函數L(w)的值最小化。權重系數的更新方式如式(10)所示：

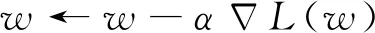
(10)

當模型訓練完成之后，需要使用測試集對模型的性能進行評估。當模型的性能較差時，則需要不斷地調整學習率、神經元個數等超參數。

3 仿真試驗

使用澳大利亞國家電力市場提供的2021年6月的電力負載數據集[16]進行仿真。原始的數據集中包含區域編號、采樣時間點、總的電力負載值和當時的電價，本次仿真試驗只使用其中的電力負載數據。該數據集包含了1 440個樣本點，每間隔30 min進行一次采樣。試驗選擇前400個樣本點進行測試。該數據集的特征如圖3所示。

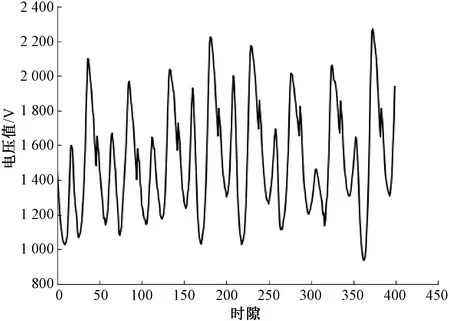
圖3 仿真數據集的特征圖

仿真使用的RNN模型包含1個輸入層、1個隱藏層(含32個神經元)、1個全連接層和1個輸出層。其中輸入層神經元的個數是2，包含t-1時刻和t-2時刻的負載值；輸出層的神經元個數是1，即t時刻的負載值。學習率α設為0.01，并以7∶3的比例將數據集分成訓練集和測試集兩個部分。此外，選擇Adam梯度下降算法來更新RNN模型中的權重系數。

3.1 不同的學習率對RNN收斂性能的影響

圖4展示了不同大小的學習率對RNN收斂性能的影響。從圖4可以看出，當學習率α的值越小時，均方誤差下降得越慢，因此需要更多的迭代次數才能讓RNN收斂。當迭代次數足夠多時，RNN模型最終都能成功收斂。但當α過大時(α=0.900時)，則損失函數達不到最低點，導致最終的均方誤差過大。因此，要適當地調整學習率α的大小才能使RNN的性能達到最優，α過小則收斂速度較慢，α過大則均方誤差較大，導致RNN最終的性能較差。

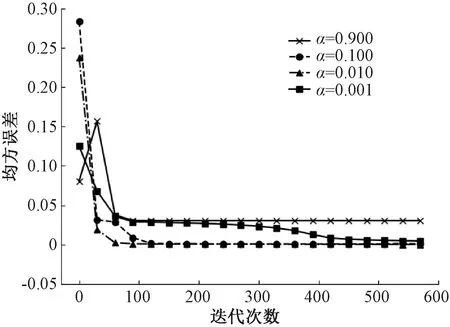
圖4 均方誤差與迭代次數之間的關系

在4種不同學習率下訓練得到的RNN模型上，利用測試集來檢驗RNN的擬合效果，并與數據集中的原始數據進行比較。圖5為不同學習率下的預測電壓值。由圖5可以看出：當學習率α為0.900時，得到的RNN性能非常差，幾乎沒有學習到電壓序列的相關特征；當α為0.010時，RNN的性能最優，得到的預測值基本上與原始的電壓序列相互重合。表1列出了在不同學習率下的測試集的均方誤差。從表中能清楚地看到，當學習率α為0.900和0.001時，均方誤差較大。前者是由于α偏大，導致權重系數在最優解的附近反復橫跳，始終無法到達損失函數的最優解。而后者是由于α過小，學習速度較慢，經過600次迭代仍無法到達損失函數的最小值。圖5和表1再次說明了學習率對RNN模型性能的重要性。

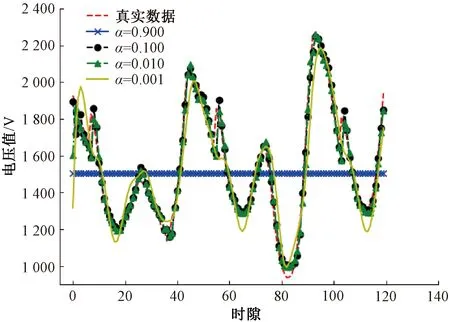
圖5 不同學習率下的預測電壓值

表1 不同學習率下的均方誤差

3.2 神經元個數對RNN收斂性能的影響

圖6為不同神經元個數下的均方誤差和訓練時長，總訓練時間為RNN模型迭代600次所需要的時間。隨著神經元個數的增加，最終得到的均方誤差會逐漸減少。這是因為神經元個數越多，RNN的結構就更復雜，擬合非線性函數的能力就越強。此外，訓練時長整體上也隨著神經元個數的增加而增加。這是因為隨著神經元個數的增加，RNN模型需要更新的權重系數的數量也會增加，導致訓練時間變長。但通過仔細觀察可以發現，當神經元的個數為32時，相比神經元個數為8這一情況，RNN模型訓練所需的時間顯著增長，但最終的均方誤差并沒有顯著減少。這就說明在訓練RNN模型的過程中，要綜合考慮均方誤差和訓練時間這兩方面的因素來選擇合適的神經元個數。

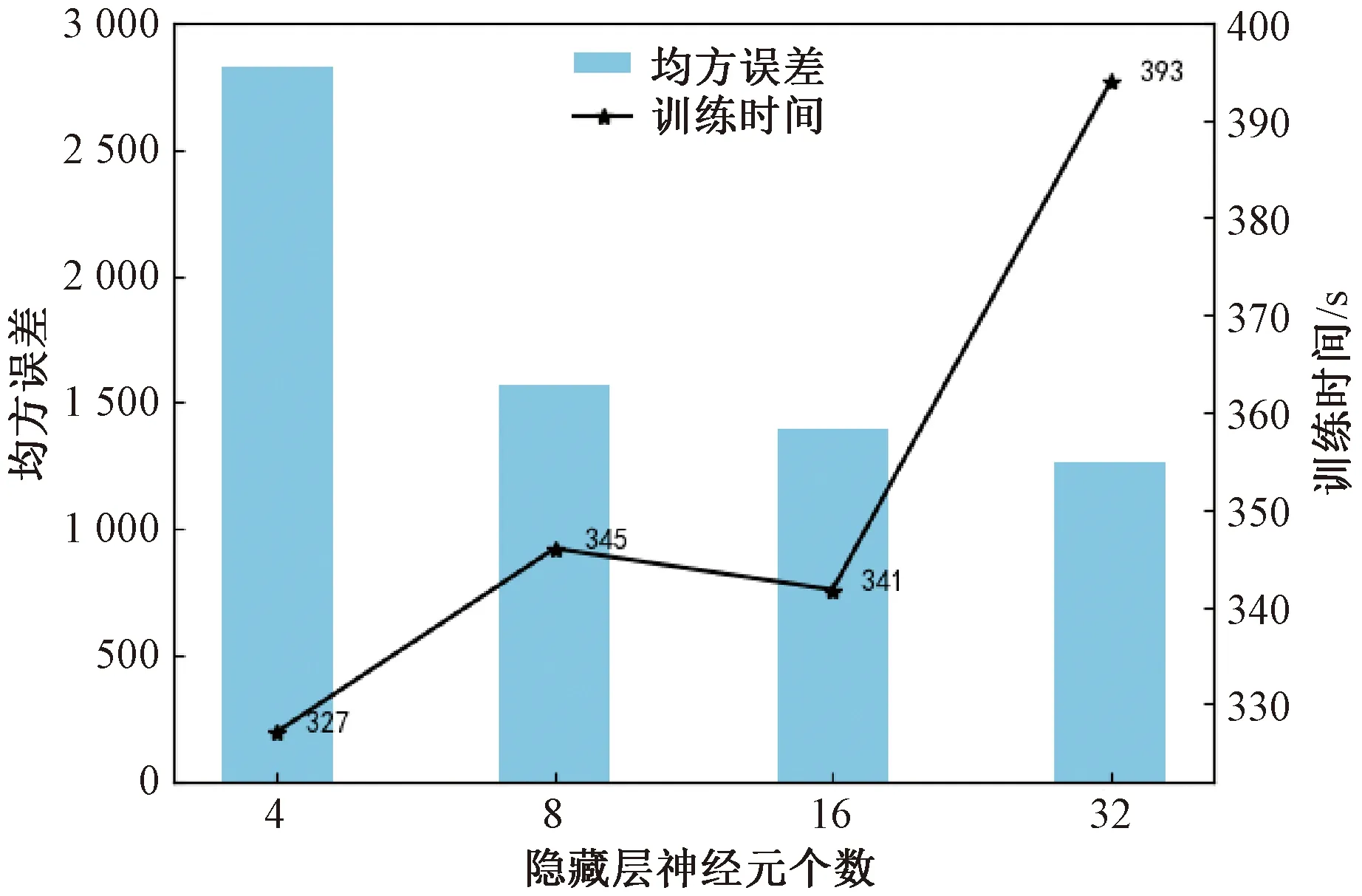
圖6 不同神經元個數下的均方誤差和訓練時間

3.3 RNN算法與ARIMA算法的比較

ARIMA(autoregressive integrated moving average)是一種常用的時間序列預測模型。該模型中需要確定3個參數的大小，即自回歸項數p、差分次數d、滑動平均項數q。在本次仿真中，針對所使用的數據集，最終確定了一組比較合適的參數值(p=1，d=1,q=2)。RNN算法與傳統的ARIMA算法[15]的性能比較如圖7所示。從圖7可以看出：RNN模型預測得到的電壓值與原始數據幾乎完全重合；但ARIMA算法的預測結果不太理想，與原始數據相差較大。這是因為ARIMA模型較為簡單，只能夠擬合線性函數，并不能很好地捕捉復雜時間序列的規律。此外，ARIMA要求預測的時間序列是穩定的，或者能夠通過取對數和差分等手段使其變成穩定的，但大部分復雜的時間序列并不滿足這一要求。RNN本身則可以擬合復雜的線性和非線性函數，也不要求時間序列具有穩定性，因此其預測的準確度遠高于ARIMA算法，適用范圍也比ARIMA算法廣。

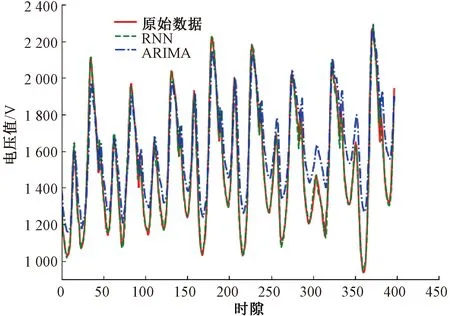
圖7 RNN與ARIMA的性能比較

表2為RNN算法和ARIMA算法的均方誤差。為了保證公平性，在計算RNN算法的均方誤差時，使用測試集上的均方誤差，并沒有考慮訓練集上的均方誤差。從表2可以看出，RNN的預測效果遠遠優于ARIMA算法，其準確度比ARIMA算法高83%。

表2 RNN和ARIMA的均方誤差

4 結 語

本文提出了一種基于RNN的在線輔助CVT電壓測量方法,該方法不需要使用海量多維度的數據，只需要使用電力系統中過去的電壓序列作為數據集。利用循環神經網絡RNN對電壓序列進行擬合和建模，把RNN的輸出作為標準值來判斷CVT的實際測量數據是否存在誤差。通過實際的數據集進行仿真和對比試驗，發現相比傳統的時間序列算法ARIMA，本文方法的性能提升了83%，證實了該方法的有效性和準確性。