基于VMD 多尺度熵與BP 神經網絡的液壓設備故障診斷

徐啟勝，江 水，李 軍，李 巖

（安徽三禾一信息科技有限公司，安徽 合肥 230123）

1 引言

液壓設備是指一系列液壓裝置的總稱，一般由動力部分、執行部分、控制部分等控制閥件和輔助部分、管路等組成，具有響應速度快、輸出平穩、功率密度大、易實現無級調速以及對復雜工況的適應性強等優點，使其在工程建設、國防、冶金礦山、材料加工等工況復雜的裝備中被廣泛采用。此類大型設備的狀態監測與故障診斷問題，不僅關乎企業的經濟效益，更關系到操作人員的人身安全與健康問題，因此對于液壓設備進行故障診斷極為重要[1]。

國內外專家學者從20 世紀80 年代起，就開展了液壓設備的狀態監測和故障診斷等機械設備健康管理研究。Aiwina Heng 等人建立一個綜合考慮失效分布的總體特性和狀態監測的個體特征模型，實現對設備的運行安全智能預測，并基于液壓泵采集到的振動信號數據驗證了該模型預測精度[2]；Jegadeeshwaran R 等人基于設計決策樹算法對液壓制動系統的突出故障特征指標進行選擇，并使用模糊分類器對不同的典型故障進行分類[3]。以上研究表明，當前國內外學者在液壓設備的故障診斷方面做出廣泛研究，基于采集的振動信號，建立相關診斷模型，可以實現液壓設備故障診斷，但依然存在相關問題。

對于振動信號進行特征提取的目的在于將原始信號中表征液壓設備實際狀態的特征準確提取，這對于液壓設備狀態評價和故障診斷具有重要意義。針對液壓設備振動信號的非線性、非平穩性和強噪聲性，常采用小波變換（Wavelet Transform，WT）、經驗模態分解（Empirical mode decomposition，EMD）等時頻分析方法進行分析[4-5]，WT 為非自適應分解算法，依靠經驗性結論選取參數以得到準確分析結果；EMD 可依據振動信號自身特性進行分解，有效避免小波基函數及分解層數人工設定，但端點效應及模態混疊問題較為明顯。變分模態分解（VMD）克服了EMD 方法存在端點效應和模態分量混疊的問題，并且具有更堅實的數學理論基礎，可以降低復雜度高和非線性強的振動信號非平穩性，分解獲得包含多個不同頻率尺度且相對平穩的子序列，適用于非平穩性的序列[6-7]。

基于熵理論的特征提取方法近年來在非線性非平穩信號特征提取中多有應用[8]，熵說明信號的復雜程度，將信號的包含的信息轉化為統計學指標，更直觀地表征信號特征。將時頻分析方法與熵理論結合的信號特征提取，對于液壓設備復雜運行環境中所采集的非平穩、非線性信號，具有良好的應用效果。王濤等[8]將EMD 與排列熵方法相結合，對于EMD 分解后的多個IMF，計算排列熵值和相關系數，根據聯合系數最大化原則對篩選出的分量進行信號重構，并利用快速譜峭度對重構信號進行濾波分析，相較于傳統的包絡解調具有更好的效果。茍先太等[9]對高速列車橫向減振器振動信號進行VMD 分解，計算互信息指標篩選的模態多尺度熵（Multi-scale entropy，MSE）特征值，采用支持向量機有效進行了故障判別。

隨著計算機技術的發展，深度學習在故障診斷領域得到了快速發展，BP（Back Propagation）神經網絡已被證明是一種非常可靠的診斷技術，具有良好的學習能力[10-11]。BP 神經網絡在故障診斷的應用是利用非線性映射的BP 網絡對非線性相關的故障進行信息收集。神經網絡的輸入參數是故障原因，輸出是故障類型，BP 神經網絡由神經元組成，通過權重系數將各個神經元相互聯系，使其具有較強的自學習能力。

因此，本文提出了一種基于VMD 多尺度熵與BP 神經網絡的液壓設備故障診斷方法。對于采集到的液壓設備振動信號，利用VMD 分解效果將信號分解到不同尺度IMF，計算有效IMF 的多尺度熵特征值并構建特征向量集，進一步輸入建立好的BP 網絡，輸出液壓設備故障分類，實現故障診斷。使用相關數據集進行驗證，本文提出的方法具有普適性且應用效果較好。

2 基本原理

2.1 VMD 算法原理

VMD 是一種新的自適應時頻分析算法。基于變分問題完全非遞歸的方式，使復雜信號分解得到多個IMF，每個具有自主中心頻率，以及有限帶寬它有堅實的數學基礎，本質上是一種特殊變異模型的迭代求解過程。VMD 理論由變分模型的建立和變分模型的求解兩部分組成。

2.1.1 變分問題構造

在EMD 理論中，固有模函數被定義為信號分量，其特征是其極端點和零交叉點的數量等于或最多不同一個，其上包絡和下包絡的平均值由任何時間點的局部最大點和局部最小點決定。為了建立信號分解的變分模型，VMD 放棄了上述定義，將IMF重新定義為調頻（AM-FM）信號uk（t），即：

Ak（t）是關于uk（t）的瞬時幅值，且Ak（t）≥0；φk（t）是uk（t）瞬時相角。對φk（t）進行求導，得到φk（t）瞬時頻率：

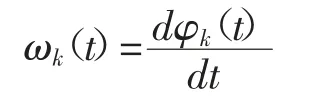
其中：ωk（t）≥0

由k 個IMF 合成一個信號f，進而針對信號f 進行變分問題構造：

（1）針對模態函數ωk（t），對其單邊頻譜進行Hibert 變換，獲得對應解析信號，即：

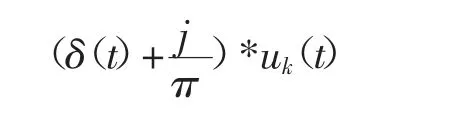
（2）基于模態函數頻譜，進行調制解調，期間加上修正系數e-jwkt即：

（3）最后計算該公式的梯度平方L2范數，算出各個模態函數uk（t）的帶寬，構建相應約束變分問題。該變分問題表示為：

式中，{uk}為分解出k 個IMF，即{uk}={u1，u2…uk};{wk}為各IMF 中心頻率，即 {wk}={w1，w2…wk}；*表示卷積；?t為函數時間導數；δ（t）為單位脈沖函數。

2.1.2 變分問題求解

為了得到變分模型的最優解，利用二次懲罰因子和拉格朗日乘數，對約束問題變換為不受約束的問題從而構造的變分問題求出最優解。

（1）上式可以看做對非約束變分問題求解，于是使用二次懲罰因子α；進一步基于Lagrange 算子λ，其為了在求解過程中，也可以確保約束條件嚴格性。從而生成增廣Lagrange 函數，公式如下：

（2）繼續求解，計算得出非約束性變分問題，即采用相互交替的方式，不斷更新ukn+1、wkn+1和λn+1，從而得到最優解，模態分量ukn+1公式如下：

（3）利用傅里葉變換定理，從而轉換至頻域處理，可以將非負頻率積分，最后計算出二次優化解，進行更新，具體表達式如下：

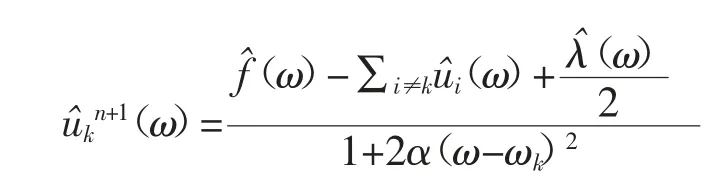
同理，也在頻域中，處理中心頻率問題，對分量中心頻率更新，具有按下式進行：

2.1.3 VMD 算法流程

對于VMD 分解求解過程，便是將模態轉換至頻域內，直接在頻域持續不斷更新，最后，采用uk（ω）傅里葉逆變換，逆轉換得到時域實部uk（t），具體流程如下：

VMD 算法流程如圖1 所示。

圖1 變分模態分解算法的流程圖

2.2 多尺度熵原理

多尺度熵算法最先由Costa 等提出，該算法基于樣本熵，從不同尺度描述信號不規則程度。通過對原始數粗粒化處理，計算得到數據序列在多個尺度下的樣本熵。對于相同尺度下的不同數據序列，樣本熵值高的序列具有更高的復雜性，由此體現數據序列之間的差異性。對于給定原始數據序列X=[x1,x2,…,xL]，L 為序列長度，其多尺度熵的由以下步驟計算得到。

（1）采用粗粒化算法處理原始序列，得到新的時間序列：

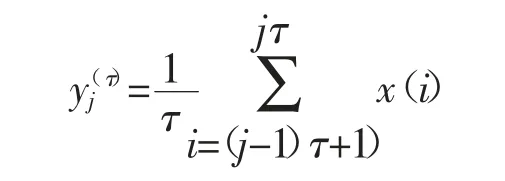
式中：j=1,2…，N，τ 為尺度因子，每一個粗粒化后的時間序列的長度N=L/τ，τ=1 時即為原始序列。

（2）將粗粒化序列組成一組m 維矢量：

式中：ij=1,2…，N-m+1，i≠j。

（4）給定閾值r（r 稱作容差，r＞0），對于每個i≤N-m+1 的值，統計的數目H 與距離總數N-m+1 的比值，記作，其平均值記作：

（5）增加維數至m+1，重復步驟（2）～（4），從而得到尺度為τ，嵌入維數為m+1 時的，求其平均值得到Cτ,m（r）；

（6）當N 為有限數，尺度為τ 時，定義樣本熵為：

多尺度熵由不同尺度的樣本熵組成集合，表示為：

多尺度熵的計算需確定嵌入維數m、相似容限r和尺度因子τ 三個參數，一般情況下，m=2，r=0.1～0.25δ（δ 為原始數據序列的標準差），τ≤20。本文選取m=2，r=015δ，τ≤16。

2.3 BP 神經網絡原理

BP（Back-Propagation）神經網絡是一種以誤差反向傳播算法訓練的多層前饋神經網絡。整體結構如圖2 所示。

圖2 BP 神經網絡結構圖

xi（i=1，2，3，…，12）為輸入向量；l 為隱含層節點數；wi為輸入層與隱含層之間的連接權值；wjk為隱含層與輸出層之間的連接權值；γj為隱含層閾值；f（x）為隱含層激活函數，激活函數使用sigmod 函數。

實現步驟如下：

（1）網絡參數初始化。網絡權值wij、wjk和閾值γj、θk的初始值取為零附近的隨機數值。

（2）計算隱含層輸出hj的公式如下：

（3）計算輸出層輸出Ok的公式如下所示：

式中：θk為輸出層閾值。

（4）誤差計算。選用交叉熵代價函數代替二次代價函數，使得訓練收斂速度更快。誤差E 計算公式如下所示。

式中：yk為期望輸出；d 表示一次輸入的樣本總數。

當E 小于期望誤差ε 或達到預設的學習次數則訓練終止，輸出訓練好的神經網絡參數模型，否則進行參數更新。

（5）輸出層權值及閾值更新。采用梯度下降法進行更新,公式如下所示：

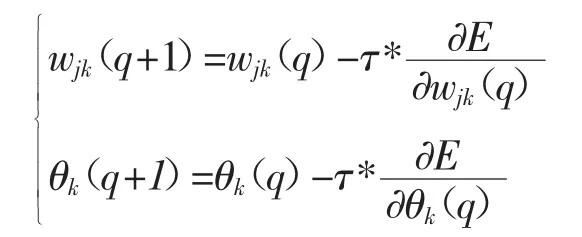
式中：q 為訓練次數。

（6）隱含層權值及閾值更新公式如下所示：

（7）網絡參數調整后，返回步驟（2）。

3 基于VMD 多尺度熵與BP 神經網絡的故障診斷

基于上述理論基礎，對于液壓設備采集的振動信號，本文將VMD 和多尺度熵的信號特征提取方法相結合，采用VMD 對原始信息進行分解，對于分解后的多個IMF，計算有效IMF 的多尺度熵特征值構成特征矩陣，劃分訓練集與測試集，將訓練集數據搭建的BP 神經網絡模型，將測試集輸入訓練完成的模型，從而獲得測試集分類結果，并計算故障分類準確率，該液壓設備故障診斷方法流程如圖3 所示。

圖3 故障診斷方法流程圖

4 實驗驗證

為驗證診斷方法的有效性，采用液壓數據進行驗證，溢流閥故障、減壓閥故障以及液壓泵故障這3種故障是液壓設備的主要故障。首先對采集到的這3種故障振動信號以及正常振動信號進行歸一化預處理，然后使用VMD 進行信號分解，VMD 參數設置如表1 所示。

表1 各類狀態信息VMD 分解參數

每個IMF 分量都包含了原始數據在不同時間尺度上的特征值信息，選擇分解后前4 個IMF 計算多尺度熵作為故障信號特征據集，其中包括4 類狀態（正常、溢流閥故障、減壓閥故障以及液壓泵故障），每類狀態都有500 個樣本，每個樣本長度為4096，共計2000 個訓練樣本。對特征數據集進行劃分：70%訓練集（1400 個訓練樣本）、30%測試集（600 個訓練樣本），在數據集種，針對液壓設備4 類狀態，分別選取其中3 個多尺度熵特征向量，如表2 所示。

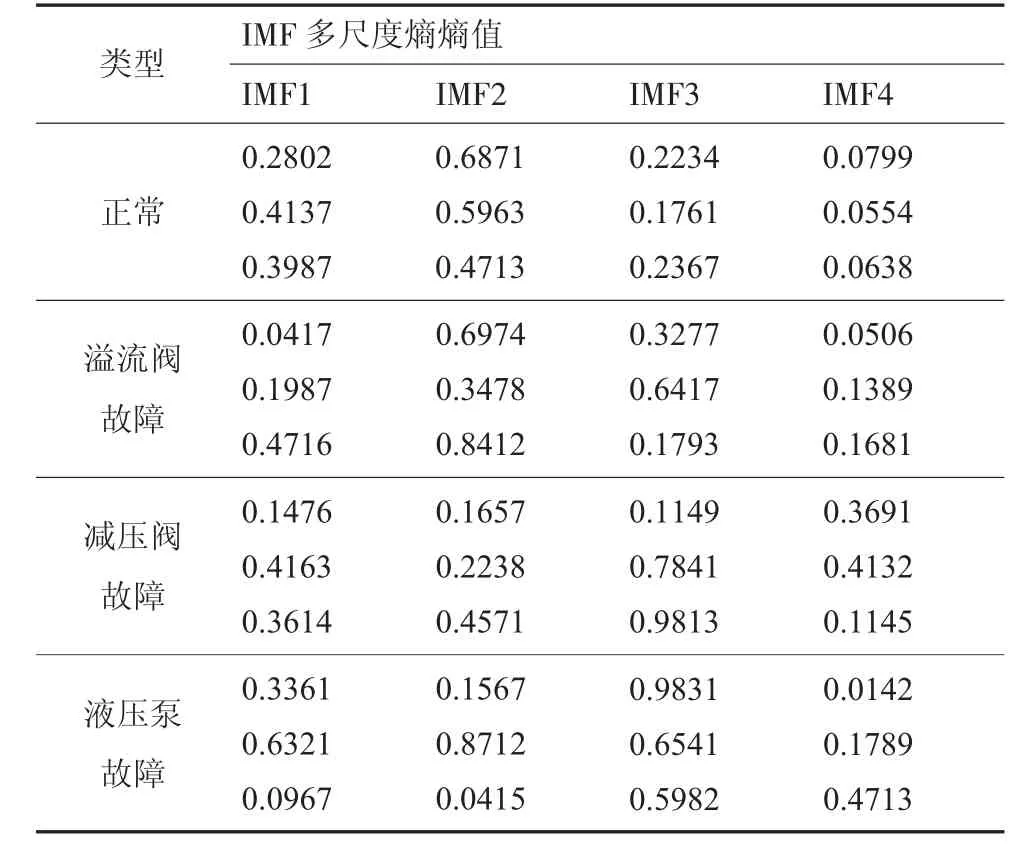
表2 數據樣本特征向量

將訓練集輸入BP 神經網絡進行訓練，實驗迭代達到最大訓練次數或者達到訓練精度，則算法終止。本方法對應所建模型參數設置如下：1 個輸入變量和1 個輸出變量，神經網絡應有1 個輸入節點和1 個輸出節點。根據Kolmogorov 定理，確定隱含層層數為2層，隱含層神經元個數為7 和13 個，激活函數為Sigmoid 函數，輸出層為Softmax 函數，最大迭代次數為1000 次，訓練均方誤差為0，訓練速率為0.005。將測試集輸入訓練好的BP 模型輸出最終診斷結果如表3 所示。從表中可以發現，在液壓設備故障診斷過程中在正常運行狀況中出現1 次誤診斷情況，其余故障在每種故障150 樣本的情況下出現小于次的誤判，故障準確率達到了96%以上。整體故障診斷準確率達到97.66%，說明該方法用于液壓設備故障具有較高診斷精度，滿足液壓設備診斷需求。

表3 液壓設備故障診斷結果

5 結論

本文提出了一種基于VMD 多尺度模糊熵與BP神經網絡的故障診斷方法，并運用于液壓設備故障診斷。VMD 具有更好的分解效果，避免模態混疊等不良表現，同時使用多尺度熵能夠有效表征不同液壓設備故障類型，為更好地進行故障診斷，使用深度學習中的BP 神經網絡，具有較高的故障診斷精度，為液壓設備故障診斷提供新的思路。