基于支持向量機理論的短期負荷預測
鄒超,盧霽明
(1.中國電建集團昆明勘測設計研究院,云南 昆明 650000;2.云南能投電力設計有限公司,云南 昆明 650000)
0 前言
電力系統短期負荷預測是電力系統安全和經濟運行的重要依據。隨著價格競爭機制引入電力系統形成電力市場后,對短期負荷預測的精度和響應速度都提出了更高的要求。雖然電力系統負荷預測的研究已有多年,形成了很多負荷預測的理論和方法[1-3],但是隨著負荷預測新理論和新技術的發展,對負荷預測新方法的理論研究仍在不斷地發展[5-6]。支持向量機理論作為數據挖掘的一項新技術,應用于模式識別[4,7]和處理回歸問題等領域。本文利用支持向量機理論良好的非線性學習及預測特性,針對電力系統短期負荷預測的各種影響因素的非線性[8-9]特點,研究基于支持向量機理論的電力系統短期負荷預測方法[10-11],具有重要的理論意義和實用價值。
1 負荷預測的樣本選擇及預處理
基于SVM的電力系統負荷預測問題的核心是尋找一個具有廣泛適用性的從影響負荷的因素到負荷的映射。實際上利用智能算法構造的負荷預測模型的性能取決于歷史負荷數據的數量和質量[12]。基于機器學習方法的SVM需要先對訓練樣本進行訓練,然后用訓練好的網絡進行預測,而預測模型的精度和泛化能力極易受樣本輸入變量的影響,因此,輸入變量的選擇問題成為電力系統負荷預測數據預處理的關鍵[13]。數據的全面性對預測的效果至關重要,本文數據選擇East-Slovakia Power Distribution Company提供的電網運行數據作為研究對象,即該數據包括1995—1998年這4年及1999年1月份每天的日平均氣溫。根據1997、1998年及1999年1月份每天24h內30min等間隔負荷采樣數據,將1997、1998年歷史數據作為訓練樣本,將1999年1月份數據視為未知數據,進行1999年1月份的日最大負荷預測。
1.1 樣本的特征選擇
電力系統短期負荷預測是一個多變量預測問題,它被作為函數回歸問題研究。預測負荷值y為函數的輸出值,而相應的影響負荷的因素如:歷史負荷、溫度信息、氣象信息等,作為函數輸入值x。訓練數據的每個成分即是SVM的特征量(樣本集(x,y)的輸入向量x中的每一個元素稱作一個特征)。不同的數據序列影響模型的方案,從而結合相關性的大小和數據決定輸入樣本的模型。本文選擇的數據特征量為:負荷時間序列、時間因素以及氣溫對負荷的影響等。
1.2 訓練和測試樣本的確定
針對基于SVM的電力系統短期負荷預測算法中特征選擇問題,許多的研究者做了很多的工作并運用多種方法來確定樣本的特征量。主成分分析(principle component analysis,PCA)作為目前常用的解決輸入變量選擇問題的方法[14],在理論和應用上都相對簡單易懂。不僅可以壓縮樣本空間和提升預測的效率,也能消除由于變量間存在相關性導致的預測模型泛化能力的降低,從而有效提高模型的預測精度。
本文根據以前的研究者所做的工作,在對歷史數據進行分析后,確定如下樣本輸入量:
1)預測日之前7天每日日最大負荷數據L={l1,l2,l3,l4,l5,l6,l7};
2)預測日的日平均氣溫T;
3)預測日的周屬性W=(1,2,3,4,5,6,7),其中的數值對應于周一到周日;
4)預測日的節日屬性F=(1.0,0.0),其值為1表征預測日為重大節假日。
輸入樣本為10維的向量{l1,l2,l3,l4,l5,l6,l7,T,W,F},對歷史數據進行平滑和歸一化處理,構成包含723個樣本的樣本集。
1.3 負荷預測步驟及預測評判標準
1)將歷史樣本進行歸一化處理,構成SVM訓練樣本集;
2)根據訓練樣本集建立如式(1)的目標函數[15];
對偶最優問題:

引入核函數解上式得:

閾值b可通過下式計算得到:

3)將數不敏感損失參數ε、懲罰系數c和核函數中的寬度參數σ2代入式(1),并求解αi、α*i;
4)將αi、α*i代入式(4),用預測樣本完成對次日日最大負荷的預測;

5)預測完成后,將次日負荷真實數據視為已知數據,依次完成全月的負荷預測。為驗證算法的有效性,本文取平均相對誤差作為預測效果評判依據,即:

式中:A(i)和F(i)分別表示實際值和預測負荷值。
2 負荷數據的歸一化問題
在獲取所有的訓練樣本和測試樣本后,由于以下因素,通常要對輸入的樣本數據進行歸一化處理:
1)避免較大范圍變化的數據淹沒較小范圍變化的數據。
2)避免計算中出現數值困難,原因是核值計算中需要計算特征向量的內積,如線性核和多項式核等,大的特征值可能會引起數值困難。
本文中歸一化是按照維來進行的,即將10維輸入向量的每一維都歸一化到所需的區間內。假設當前維在所有樣本上的最大值是max,最小值是min,則可以作如下線性變換:
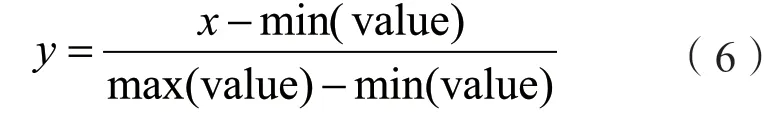
x、y分別為變換前、后的值max(value),和min(value)分別為樣本的最大值和最小值,這樣就把[min,max]區間映射為[0,1]區間了;同理,也可以將數據通過規范化的映射到區間[-1,1],此過程可由matlab的歸一化函數完成。
3 核函數選取及參數優化方法
核函數的選擇對負荷預測的精度有很大的影響。根據相關研究,本文選擇RBF作為SVM的核函數。通過大量實驗研究發現,核函數中的寬度參數σ2和懲罰系數c,對SVM的性能表現起著非常重要的作用[16]。
SVM的參數選擇對模型性能有很大的影響,目前SVM的參數選擇還沒有公認有效的結構化方法。本文由于訓練樣本的數據量較大,只對對SVM的性能表現非常關鍵的兩個參數進行尋優,即核函數中的寬度參數σ2和懲罰系數c。為確保計算的效率和實用性,本文采用網格搜索(Grid-search)和交叉驗證法(Grid-search)對核函數中的寬度參數σ2和懲罰系數c進行選擇。
交叉驗證(Cross Validation,CV)是用來驗證分類器的性能的一種統計分析方法,基本思路是把在某種意義下將原始數據(dataset)進行分組,一部分做為訓練集(train set),另一部分做為驗證集(validation set),先用訓練集對分類器訓練,再利用驗證集來測試訓練得到的模型(model),以此作為評價分類器的性能指標。常用的CV方法為k倍交叉驗證(k-fold Cross Validation),記為k-CV。交叉驗證和參數尋優是兩個步驟,它們的關系是,在參數尋優的過程中,每次得到一個新的參數值,都需要用交叉驗證去驗證。
本文的思路是在寬度參數σ2和懲罰系數c組成的二維均勻劃分的網格上確定最優值。在用SVM進行負荷預測的參數尋優和交叉驗證過程如圖1、圖2所示。

圖1 交叉驗證的第一次迭代過程

圖2 交叉驗證的第二次迭代過程
運用SVM對本文實例分別對選擇參數后和未選擇參數兩種情況下進行負荷預測,其結果如圖3和圖4所示。
由驗算結果可以得出結論,使用優選參數后的預測精度顯著提高,參數的選擇對負荷預測效果有較大的影響。現將基于SVM的電力系統負荷預測結果與真實結果繪于圖4,經計算eMAPE=1.8937%,精度較高。

圖4 未選擇參數預測結果比較
4 結束語
本文著重研究了SVM方法負荷預測模型中非常關鍵的樣本選擇及預處理問題。通過對所選歷史負荷數據與預測負荷數據相關性的研究,為樣本輸入特征量的選擇提供依據,并給出了樣本集選擇方案。此外,本文還研究了數據預處理、核函數構造及選取、參數優化的方法、數據歸一化的處理等其他問題,并采用實例分析各樣本處理情況下基于SVM的短期負荷預測的結果。研究表明,應用SVM進行電力系統負荷預測,具有精度高、速度快等優點,顯著提高了負荷預測的效果。

