50 kW雙透平氣浮轉子系統動力學特性研究

楊 維，翟曉宇，賈 華，王 雨，張 理，吳永鵬，劉延俊,

（1.山東大學海洋研究院，山東 青島 266237； 2.山東大學機械工程學院，高效潔凈機械制造教育部重點實驗室，山東 濟南 250061； 3.南方海洋科學與工程廣東省實驗室（湛江），廣東 湛江 524000）

海洋作為一個藍色經濟體，儲藏著巨大的能源。溫差能是其中一種儲量巨大、能量穩定的清潔能源，發展海洋溫差能對實現海洋強國戰略具有重大意義[1-3]。海洋溫差能發電基于有機朗肯循環發電原理：表面溫海水在蒸發器中加熱工質使其蒸發，工質氣體推動透平轉動，從而帶動發電機旋轉發電；深層冷海水在冷凝器中對乏氣進行冷凝，使得氣體工質冷凝成液態，如此循環[4]。透平是有機朗肯低溫發電系統的關鍵部件，其所使用的氣體軸承具有剛度低、阻尼小的特性，在高速運行過程中，系統可能會產生旋轉失穩，因此有必要對整個氣浮轉子系統進行動力學分析。

目前國內外學者開展了很多對轉子系統動力學特性的相關研究。譚峰等[5]對微型數控車床主軸進行了動力學特性研究，將軸承等效成彈簧單元，得出主軸的模態參數并驗證了設計的安全性。巫少龍等[6]以高速電主軸為研究對象進行模態分析，振型分析結果表明，前支承剛度對電主軸系統的影響非常明顯，提高前支撐剛度能夠提高系統的臨界轉速，避開共振區，同時能有效地提高主軸的動態性能。李文龍[7]對向心透平軸系進行了模態分析，根據模態振型確定了危險面，并對其進行了諧響應分析，得出系統的幅頻特性曲線以及最大應力隨頻率的變化曲線，確定了透平的安全轉速范圍。李健[8]建立了氣體軸承-轉子系統的動力學數學模型，采用縮減法求解了氣浮轉子系統的動力學特性，并驗證了系統能夠滿足低溫、高速旋轉的需求。許文芳等[9]基于向心透平轉子系統，利用ANSYS軟件分析得出，軸承支撐剛度對系統的臨界轉速影響較大，而軸承跨距對其影響不明顯；同時得出軸端伸長量應該保持在一定范圍內。蔣雷等[10]以采用空氣靜壓軸承為支撐的小型氣浮主軸為研究對象，利用Fluent軟件分析了氣膜壓力分布，研究軸承結構參數對其承載能力的影響規律，并對氣浮轉子系統進行了模態分析，驗證了主軸滿足設計要求。李樹森等[11]在ANSYS中建立了氣浮主軸的動力學模型，通過模態分析和對氣體軸承壓力分布仿真分析，驗證了軸承參數值的合理性，并得出主軸不會發生共振、能保持穩定運行的結論。喻麗華等[12]建立了高速電主軸氣浮轉子系統數學模型并分析了系統的不平衡質量力和磁拉力所產生的不平衡激勵；同時通過諧響應分析得出，系統在不平衡激勵下能保持穩定運行，對系統的影響較小。張楠等[13]建立了高速泵轉子系統動力學模型，研究了系統不平衡響應的影響因素，分析得到通過控制動平衡、增大轉子剛性、改變支承位置等手段可以減小系統的振幅。

目前國內外學者進行的相關研究基本是基于單透平轉子的動力學分析研究，而基于雙透平轉子系統的研究少之又少，因此雙透平轉子系統的動力學分析研究具有重大的研究意義和工程價值。本文基于50 kW雙透平轉子系統，建立了氣浮轉子系統動力學模型，首先對雙透平轉子系統進行模態分析求解出系統的臨界轉速以及固有頻率；然后基于模態分析進行諧響應分析，得到了透平葉輪徑向幅頻響應曲線；最后對葉輪進行離心應力分析，驗證了透平能保持穩定安全運行。本研究可為氣浮轉子系統的試驗、進一步的動力學分析以及優化分析提供一定的理論依據。

1 向心透平及轉子系統結構

轉子系統結構如圖1所示。透平葉輪及轉軸的材料參數見表1,透平的一維設計參數見表2。

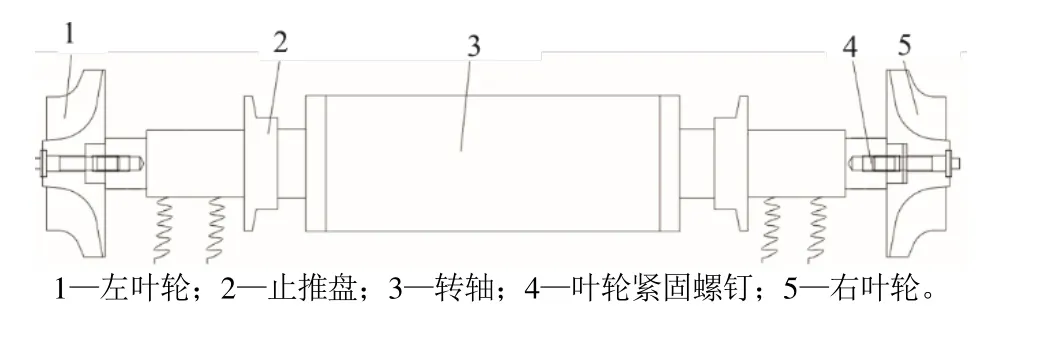
圖1 轉子系統結構Fig.1 Structure of the rotor system

表1 葉輪和轉軸材料參數Tab.1 Material parameters of the impeller and rotating shaft

表2 透平一維設計參數Tab.2 One-dimensional design parameters of the turbine

2 氣浮轉子系統模型建立

2.1 系統模型建立

氣浮轉子系統的運動方程可表示為：

式中：M為系統質量矩陣；C為系統阻尼矩陣；K為系統剛度矩陣；ft為系統所受外力；分別為系統運動的加速度、速度、位移。

對氣體軸承-轉子系統進行臨界轉速以及固有頻率分析時，應該忽略轉子系統所受外力的影響，只考慮系統自身特性[14]。而氣體軸承具有阻尼小、氣體黏度低的特點，因此可以忽略阻尼對轉子系統的影響。氣體軸承-轉子系統忽略外力、忽略阻尼影響的運動方程式為：

假定轉子系統在各個方向上作簡諧振動，即

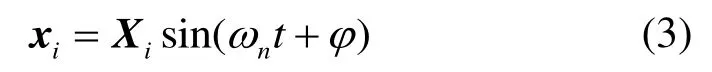
式中：Xi為振動幅值，與時間無關，反映了轉子系統的振動型態；ωn為系統的固有頻率；xi為系統自由振動時的振幅向量；t為時間；φ為初相位。

式(3)對時間進行二次求導之后代入式(2)中可以得到：

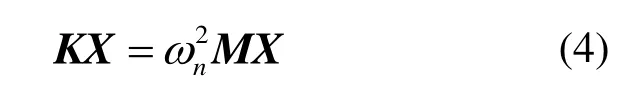
式中：X為與時間無關的振動向量。

求解式(4)系數矩陣的行列式，即

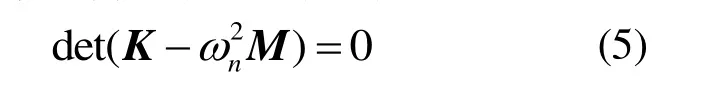
求解得到ωn的n個值，其值從小到大的排序即表示轉子系統的各階固有頻率[15]。

2.2 氣體軸承等效物理模型建立

雙透平轉子系統采用的是2個雙排供氣的靜壓氣體軸承，每排供氣孔數為8個。通過給氣體軸承的供氣孔供氣，形成氣膜支撐使得軸與軸承分離，從而支撐主軸的高速旋轉運動。氣體軸承結構示意如圖2所示。

圖2 氣體軸承結構示意Fig.2 Schematic diagram of the gas bearing structure

由于只考慮了靜壓氣體軸承的徑向剛度，而忽略了軸承的交叉剛度以及軸向剛度；并且因為氣體介質的黏度低，因而也忽略了阻尼的影響：因此，將氣體軸承支承特性等效成彈簧單元。等效后的物理模型如圖3所示[16]。其中轉軸的質量為m，每個等效彈簧的剛度為k。

通過上述兩種手段，伊朗的石油出口量大幅降低。在2012年開始的美國對伊朗制裁過程中，伊朗石油出口量由每天250萬桶降低到80萬桶，對伊朗經濟造成巨大打擊。數據顯示，2017年，中國從伊朗進口的石油約占伊朗石油出口總量的1/3，約占中國原油進口總量的11%。美國對伊朗實行制裁以來，中國已開始減少伊朗的石油進口量。雖然近日美國宣布豁免8個國家進口伊朗石油180天，其中，中國的進口量為36萬桶/日，但該項豁免是暫時的，美國的目標是將伊朗石油出口量降至零。面對美對伊制裁的步步緊逼，我國石油企業的貿易渠道將不得不進行重新布局。

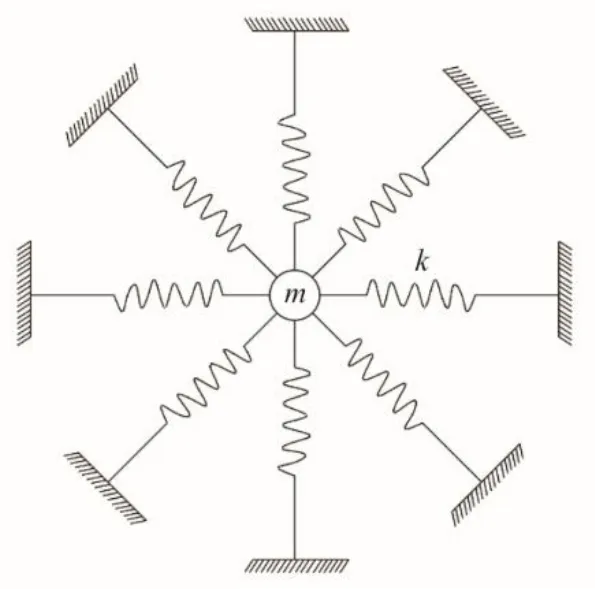
圖3 系統等效物理模型Fig.3 The equivalent physical model of the system

2.3 模型邊界條件設置及網格劃分

本文將靜壓氣體軸承等效為沿圓周雙排布置，位于氣體軸承供氣孔位置的彈簧單元來模擬氣體軸承的支承特性。每個等效彈簧單元的剛度等于氣體軸承的徑向剛度[17]，對軸系施加軸向位移約束；其余為自由態。

2.4 臨界轉速分析

利用ANSYS分析軟件，采用BlockLanczos法求解出雙透平轉子系統的模態參數。在ANSYS求解過程中，對轉子系統進行多載荷步模態分析，可得到各階渦動曲線及轉子系統的Campbell圖，如 圖4所示。

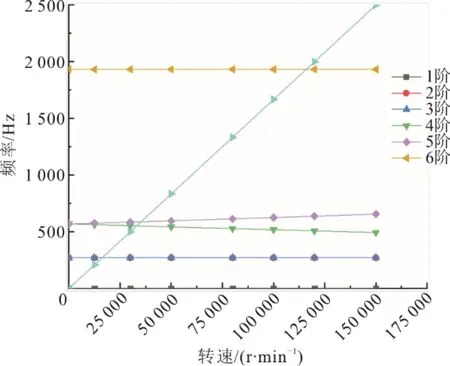
圖4 轉子系統Campbell圖Fig.4 The Campbell diagram of the rotor system

系統臨界轉速與固有頻率的關系為：

式中：nc為臨界轉速，r/min；f為固有頻率，Hz。

由于本文設計的雙透平工作轉速為12500.0 r/min，高階固有頻率對于分析系統的動態特性意義不大，故僅選取了前6階臨界轉速。雙透平轉子系統前 6階臨界轉速及固有頻率見表3。由表3可知：隨著雙透平轉子系統階次的升高，其固有頻率也隨之升高；轉子系統的1階固有頻率值接近0，為主軸繞軸心旋轉模態；2階、3階臨界轉速分別為16241.0、16242.0 r/min，固有頻率值幾乎一致，原因是透平葉輪是一種循環對稱結構，故轉子系統有重頻。2階臨界轉速高于透平設計轉速的23%，符合不低于20%的安全裕度要求[18]。當系統處于高速運轉狀態時，轉子系統會出現旋轉預應力，使得系統發生變形，對轉子系統的固有頻率造成一定的影響，因此要將旋轉預應力的影響考慮在內，不能忽略其對系統的影響[19]。

表3 雙透平轉子系統前6階臨界轉速及固有頻率Tab.3 The critical speed and natural frequency of first-6-order of the dual-turbine rotor system

考慮轉子系統高速旋轉產生的離心力后，轉子系統的2階、3階、6階固有頻率基本無變化；然而系統在旋轉預應力的作用下，4階固有頻率增加，而5階固有頻率下降。

圖5為臨界轉速與氣體軸承支承剛度的關系曲線。由圖5可知，當氣體軸承剛度取值在10～ 120 N/μm時，隨著剛度的增大，系統的2階臨界轉速隨之增大。針對12500.0 r/min這一設計工作 轉速，選取合理的軸承剛度不僅可以避免共振，而且對整個雙透平轉子系統安全穩定高效的運行尤為重要。

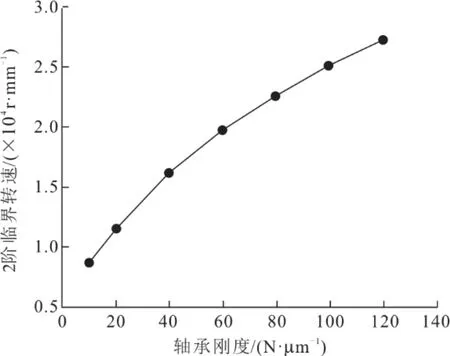
圖5 臨界轉速與氣體軸承支承剛度關系曲線Fig.5 The relationship curve between critical speed andsupporting stiffness of the gas bearing

3 諧響應分析

諧響應分析是一種分析系統在受到周期性載荷時得出系統的峰值響應特性的仿真分析方法[20]。通過仿真分析可以得到系統的幅頻特性曲線，找到峰值響應點。避開此頻率值，從而能夠避免系統產生共振及其他受迫振動而帶來的影響。

由于葉輪在實際工作中，透平葉片會受到氣流激振力的沖擊，當沖擊激振力的頻率與轉子系統的固有振動頻率相同時會導致系統發生共振，嚴重時會直接導致葉輪發生破壞，因此必須對雙透平轉子系統進行諧響應分析。激振力載荷主要是指透平工作時葉輪所受到的扭矩。通過對透平進行CFX仿真計算，可以得到扭矩的大小為32.2 N·m。假設葉輪受到的扭矩按正弦形式（圖6）發生變化，幅值為32.2 N·m，仿真分析時將扭矩直接加載在葉輪上，根據轉子系統的前6階固有頻率，取激振力頻率的范圍為0～2000 Hz。

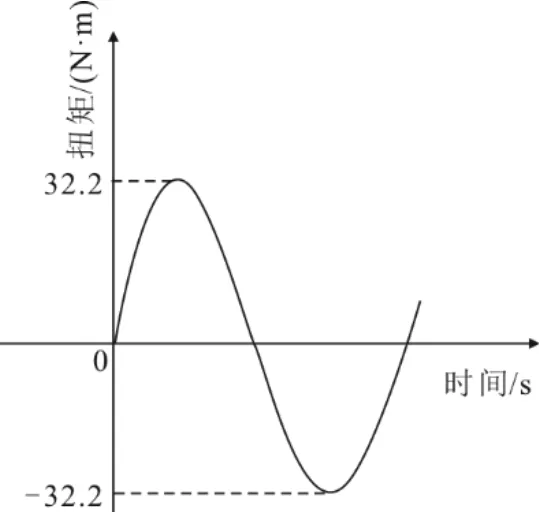
圖6 葉輪所受扭矩變化形式Fig.6 The variation of torque on the impeller

圖7為葉輪徑向振幅隨頻率變化曲線。由圖7可見：葉輪徑向振動幅值在外界激振力頻率為10、1380 Hz下時出現極大值，分別為0.0245、0.0125 mm；而在其他頻率下，葉輪能保持穩定運行。由表2可知，葉輪與噴嘴之間的裝配間隙為1 mm。葉輪在受到上述激振力頻率時產生的最大振幅遠小于裝配間隙，因此不會與噴嘴發生碰撞現象。

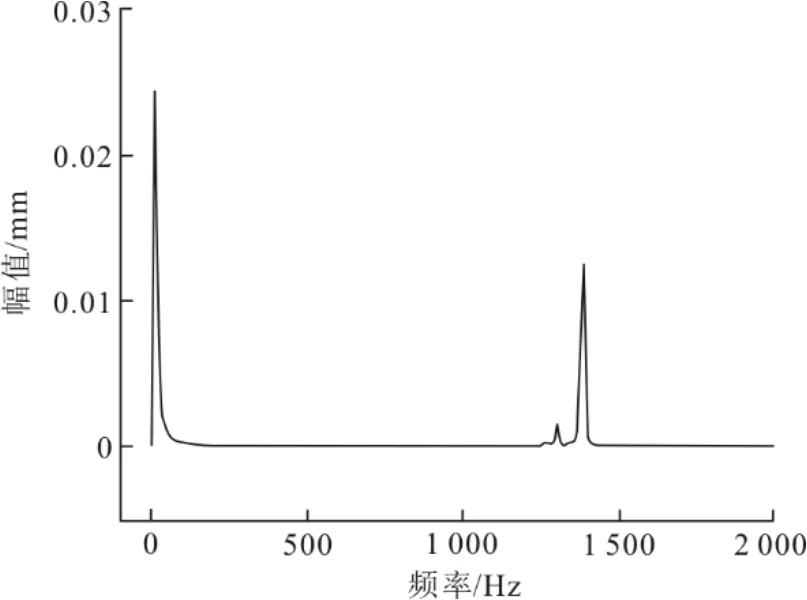
圖7 葉輪徑向振幅隨頻率變化曲線Fig.7 The variation curve of the impeller radial amplitude with frequency

4 離心應力分析

4.1 網格劃分及定義約束條件

葉輪采用四面體網格進行劃分，劃分的網格尺寸為2 mm。劃分后的節點數為308322，單元數為196814，網格質量良好。

葉輪添加的載荷為12500.0 r/min。根據葉輪在軸上的裝配關系，實際運行過程中對葉輪定義的約束為：對透平葉輪的軸孔面處添加徑向位移約束，前端面、背面添加軸向位移約束，其余方向為自由態。

4.2 結果分析

圖8為透平葉輪變形。由圖8可知，葉輪最大變形發生在葉片出口的葉尖位置，大小為0.0326 mm，且從葉片頂部到根部逐漸減小。

圖8 葉輪變形Fig.8 The impeller deformation

圖9為透平葉輪等效應力。由圖9可知，葉輪最大應力發生在葉片出口端靠近軸孔的根部，大小為12.481 MPa，低于LD5材料的屈服極限（215 MPa），故葉輪不會產生疲勞破壞。圖10為透平葉輪徑向應力。由圖10可知，葉輪最大徑向應力發生在葉片出口端靠近軸孔的根部，大小為11.9 MPa。圖11為透平葉輪環向應力。由圖11可知，最大環向應力發生在葉輪軸孔底部靠近邊緣的位置，大小為9.73 MPa。

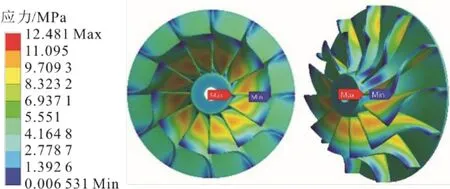
圖9 葉輪等效應力Fig.9 The equivalent stress on the impeller

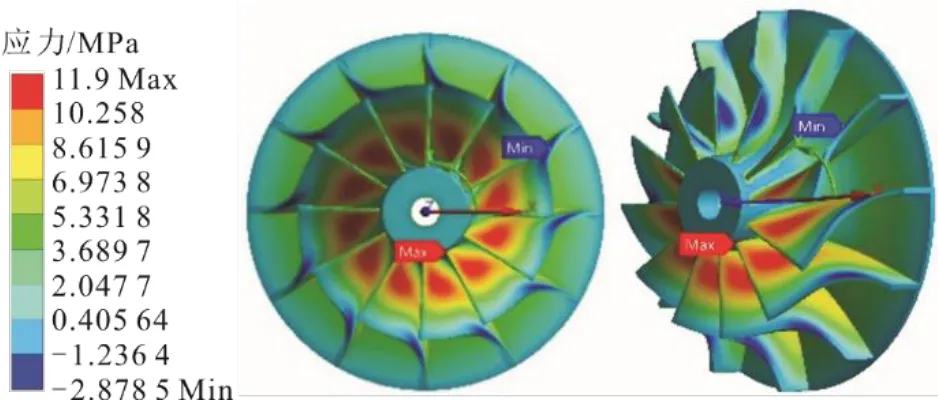
圖10 葉輪徑向應力Fig.10 The radial stress on the impeller

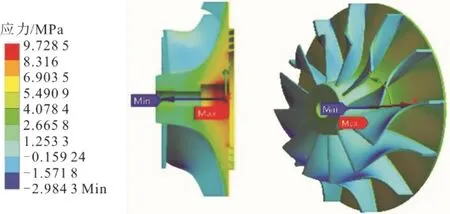
圖11 葉輪環向應力Fig.11 The circumferential stress on the impeller

5 結論

1）轉子系統采用雙透平結構，基于ANSYS仿真得到，轉子系統的2階臨界轉速為16241.0 r/min，而設計的工作轉速為12500.0 r/min，符合安全裕度。

2）雙透平轉子系統2階臨界轉速隨氣體軸承支承剛度的升高而升高，故選取合理的氣體軸承至關重要；由于離心力而產生的旋轉預應力對系統的固有頻率造成一定的影響，分析得出轉子系統的 4階、5階固有頻率隨之發生了變化。

3）對雙透平轉子系統進行諧響應分析，仿真得到了透平葉輪徑向振動幅值隨頻率的變化曲線，得到葉輪振動幅值最大時所對應的頻率值。分析可知，葉輪在受到此激振力時不會發生葉輪和噴嘴之間的碰撞，透平轉子系統能保持穩定的運轉。

4）葉輪作為透平的核心部件，對其進行離心應力分析，找到葉輪可能發生破壞的薄弱點，并分析得出葉輪在此工作轉速下不會發生破壞。