干濕循環作用下土質邊坡穩定性分析
李紅曉,李朝暉
(河南省水利第一工程局,鄭州 450000)
邊坡工程是工程界常見的基礎性工程結構,其安全性至關重要。大多數邊坡均由飽和與非飽和土組成,非飽和土由三相構成,力學性質復雜。目前,工程計算中常忽略非飽和土的氣相,只考慮固液兩相,這樣會使計算結果產生較大的偏差。通過地表的蒸發作用,土體中的液相會以蒸汽的形式運移,而土體含水率的變化直接影響著巖土體結構的穩定性,如土質路基的不均勻沉降和邊坡的失穩等[1]。生活中邊坡穩定倍受廣大工程人員以及科研工作者的關注,近年來因土質邊坡失穩造成的重大災害常常出現。隨著計算機的發展,數值計算可考慮的因素也越來越多,在邊坡穩定分析時,將水氣運移而引起的土體含水量變化考慮在內可大大提高仿真計算的精度,為工程設計和施工提供了精度較高的邊坡穩定安全系數計算結果。降雨給土體補水,土體通過吸濕作用使體積含水率增加,而大氣蒸發使表層土體含水率降低。入滲和蒸發作用帶來的干濕循環使邊坡的穩定性處于動態變化之中,應對安全系數的變化進行量化計算。韋杰等[2]使用數值方法計算了大氣-陸地交互作用對滲流場的影響;劉金龍等[3]建立了土坡在入滲條件下的數值計算模型。
本文基于考慮蒸氣項的非飽和土滲流控制方程、非飽和土抗剪強度理論以及極限平衡法,建立干濕循環作用對土質邊坡穩定影響的數值分析模型,對某土質邊坡安全系數進行量化分析,計算結果可為同類工程提供相關借鑒。
1 基本理論
1.1 考慮蒸氣項的非飽和土滲流控制方程
傳統的滲流場控制方程忽略水氣運移,只考慮固液兩相。WILSON[4]給出了考慮水氣運移的二維飽和非飽和滲流控制方程:
(1)
式中:uw為孔隙水壓力;kx和ky為滲透系數;t為時間;Q為邊界流量;mw為比水容重;ρ為水的密度;Dv為氣體擴散系數;Pv為蒸氣壓。
考慮水氣運移的滲流過程需另外考慮熱的傳遞,相應熱傳導方程[5]如下:
(2)
式中:Lv為汽化潛熱;T為溫度;Qt為熱量源匯項。
1.2 非飽和土滲透系數模型
非飽和土的滲透系數是負壓的函數,常使用數學模型來描述。本文使用Van Genuchten模型來擬合非飽和土的土水特性參數,相關函數表達式如下:
(3)
式中:θr和θs分別為殘余和飽和含水量;α、m、n為曲線特征參數。
(4)
式中:K(ψ)為負壓為ψ時的滲透系數。
1.3 蒸發邊界條件
本文使用Penman-Wilson提出的蒸發模型作為表層土體蒸發的邊界條件[6-7],該模型表達式如下:
(5)
式中:E和Ea分別為實際與潛在蒸發強度;Γ為飽和蒸汽壓-溫度曲線的斜率;Q為凈輻射量;v為濕度常數;Ea=f(u)Pa(B-A);f(u)為風函數。
2 實例分析
現以某簡單邊坡為例,分析干濕循環作用對邊坡穩定的影響。圖1為邊坡的有限元模型,共剖分1 469個節點、1 380個單元。地下水位埋深距坡腳深度10 m。

圖1 計算模型示意圖
2.1 計算參數的選取
2.1.1 土體參數
邊坡土體主要為砂質黏土,數值分析過程中土體的相關物理力學及熱力學參數見表1,土體的土水特征則用VG模型來表征,吸濕曲線和脫濕曲線相同,見圖2。土體的熱學模型參考文獻[8]選取,體積比熱系數為2.24×103kJ/(m3·℃),熱傳導率系數為0.006 kJ/(s·m3·℃),邊坡土體的初始溫度全部預設為20℃。

圖2 滲透系數與土水特征曲線

表1 土體物理力學參數匯總表
2.1.2 氣候參數
氣候參數使用實測數據,數據取自南京某年7月份的氣象監測數據,見圖3。并以此作為Penman-Wilson蒸發模型的輸入參數,從而計算表層土體的實際蒸發強度[9]。
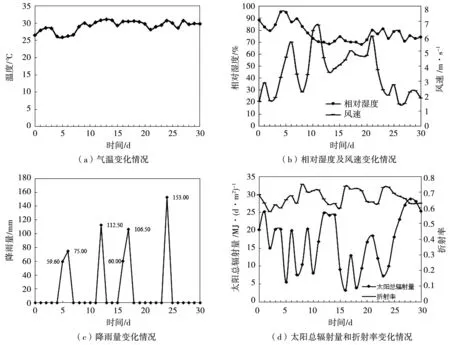
圖3 實測氣候數據
2.2 計算結果及分析
2.2.1 坡腳含水率變化
選取一個降雨周期(前11天)對坡腳處土體的含水率變化進行分析。從圖 3(c)可以看出,前5天均為晴天,主要為地表蒸發作用;第6天第一場降雨,日降雨量59.6 mm;第7天持續降雨,日降雨量75 mm;第8-11天無降雨,以蒸發作用為主。
邊坡坡腳及以下5 m土體的含水率隨時間的變化見圖4。從圖4中可以看出,前5天均以蒸發為主,表層土體隨蒸發逐漸變得干燥,并接近殘余體積含水量;第6、第7天有降雨,坡腳土體含水量增加并接近飽和;第8-第11天以蒸發為主,坡腳淺層土體因為蒸發作用逐漸變干。地面以下1.25 m內的土體含水量變化呈現出相似的規律,但相較于表層土體具有一定的滯后性,更深層土體的含水量受氣候作用影響不大。
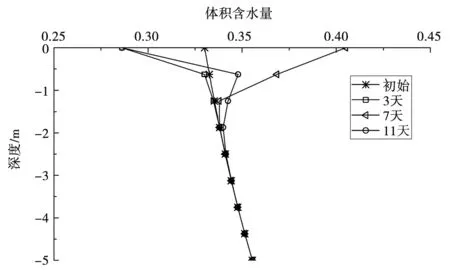
圖4 坡腳土體體積含水量變化情況
2.2.2 滲流場變化
圖5為邊坡初始時刻、第3天、第7天以及第11天的滲流場云圖。從圖5中可以看出,數值計算剛開始的時候邊坡孔隙水壓力均勻分布,自由水面以上土體孔隙水壓力為負值,隨著表層土體水分的蒸發,土表負孔壓逐漸增大。第6天降雨后,表層土體吸濕,負的孔壓減小,第8-第11天規律與前5天類似。從計算結果可以看出,蒸發降雨作用對邊坡的瞬態滲流場分布具有重要的影響,考慮水氣運移可大大提高邊坡滲流場的計算精度。

圖5 坡腳土體體積含水量逐日變化云圖
2.2.3 邊坡安全系數變化
在邊坡瞬態滲流場結果的基礎上,使用極限平衡方法來獲得邊坡的抗滑穩定安全系數。數值計算時,第6、第7、第13、第18、第25天有降雨,其余各天均以地表蒸發為主。圖6為邊坡安全系數變化情況,圖7為第5天和第7天的邊坡安全系數和滲流場分布云圖。從計算結果可以看出,土體蒸發可在一定程度范圍內提高邊坡穩定性,而降雨入滲則有相反的作用。主要原因是蒸發引起的水氣運移使土體非飽和區的含水率大大降低,非飽和區負壓增大,從而使邊坡安全系數增加,而降雨則作用相反。在數值模擬的一個月內,邊坡安全系數在干濕循環的作用下,整體上呈現下降趨勢,最小值1.655出現在第25天。
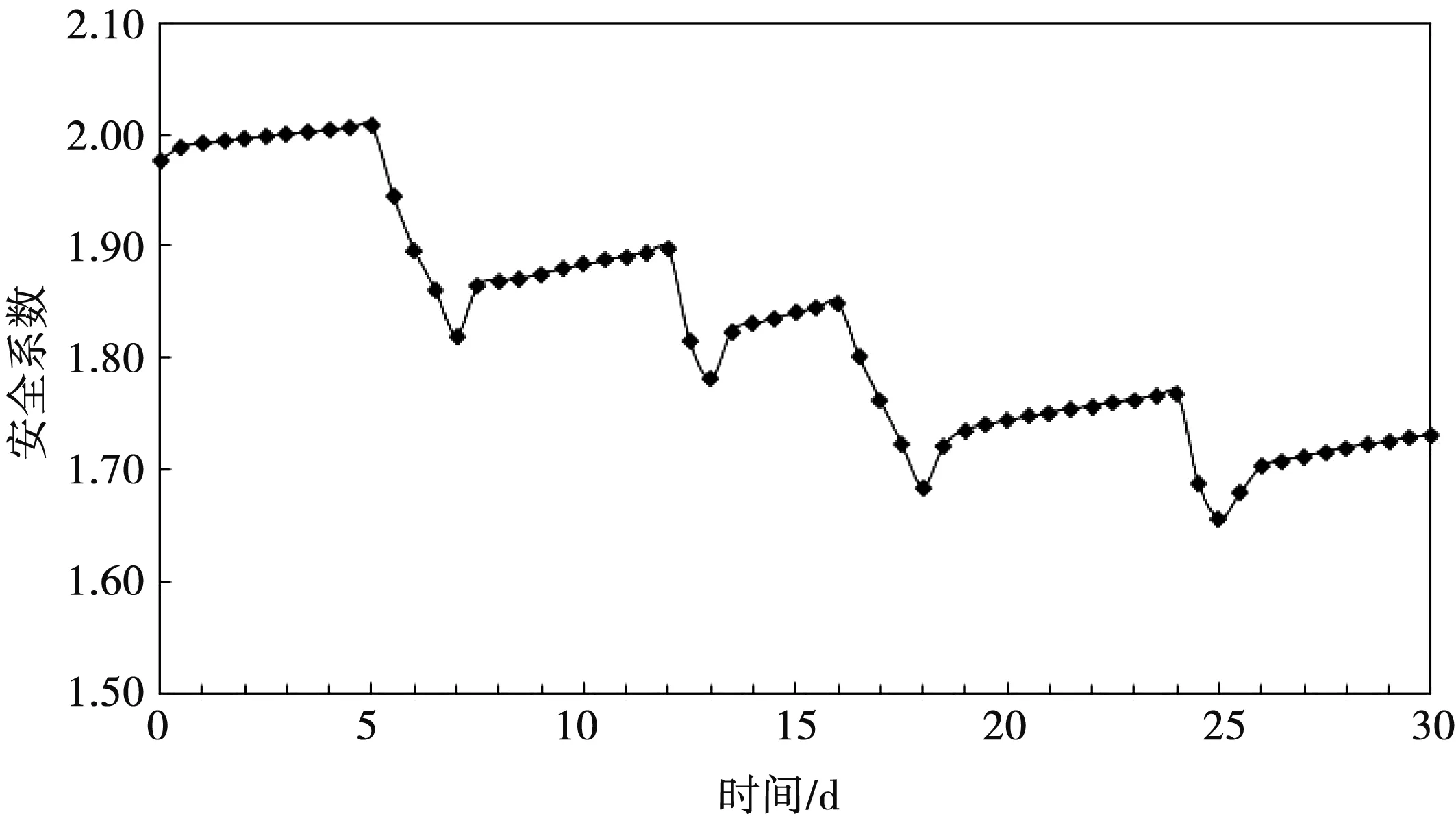
圖6 邊坡安全系數逐日變化情況
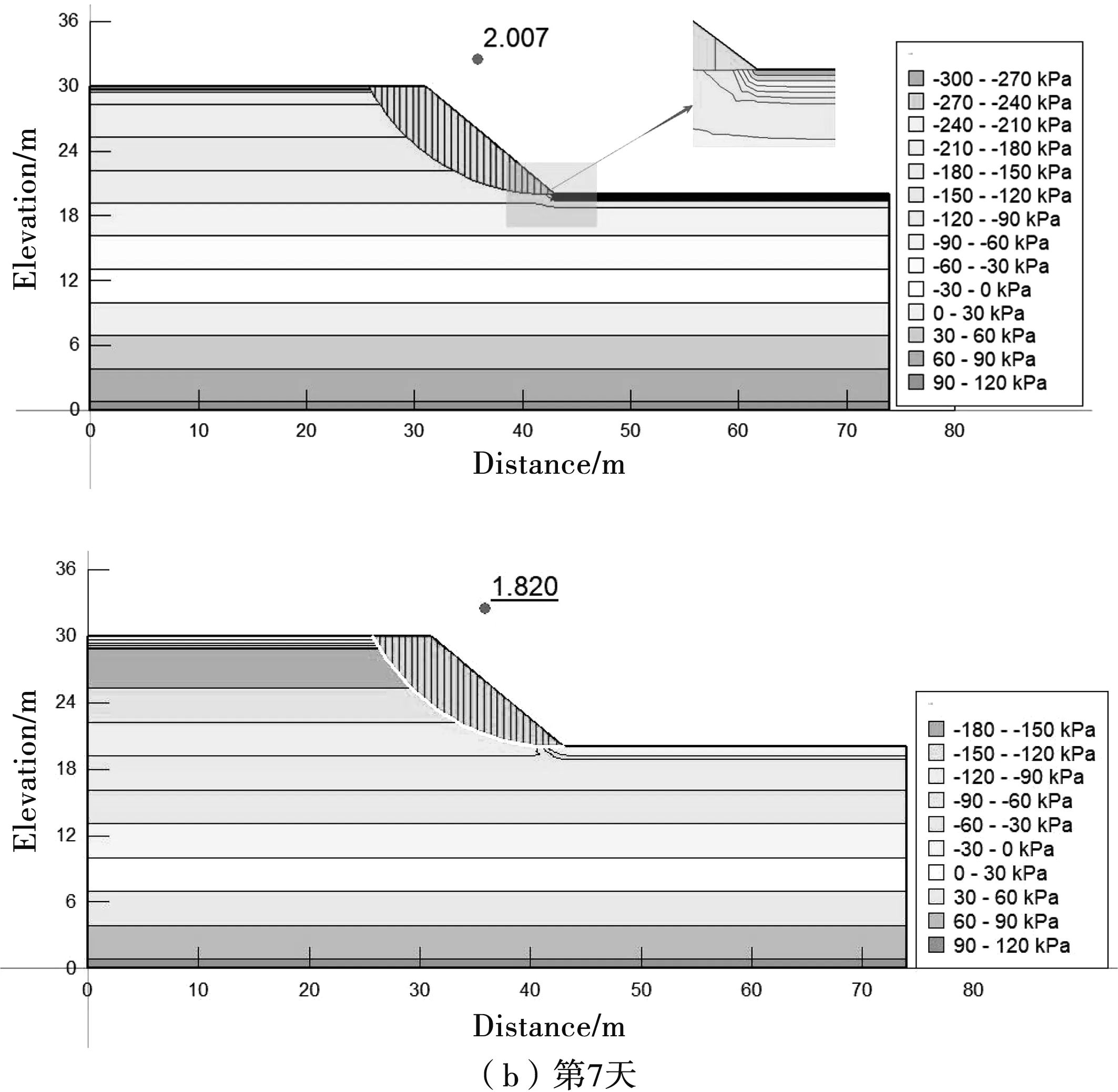
圖7 第5、第7天邊坡安全系數
3 結 論
1) Penman-Wilson蒸發模型將氣溫、風速、土體含水率等諸多因素考慮在內,可以較好地模擬土體表層的實際蒸發過程。
2) 地表蒸發作用使非飽和區土體含水率減小,負的孔隙水壓力增加,而降雨入滲則表現出相反的作用。干濕循環作用對邊坡的穩定性具有重要影響,干濕循環使非飽和土體負的孔隙水壓力發生循環往復,安全系數也隨之往復變化,但從模擬結果可以看出,邊坡安全系數在整體上呈現下降趨勢。

