百千瓦級空間鋰冷快堆系統熱工安全特性研究

金 釗，王成龍，劉 逍，代智文，田文喜，秋穗正，蘇光輝

(西安交通大學 核科學與技術學院，陜西 西安 710049)

隨著空間探索任務要求的不斷提高，空間探測器將面臨更為極端的空間環境，傳統太陽能供電難以滿足深空探測的需要，大功率空間核反應堆已成為未來太空能源的主要發展方向[1]。

空間核電源的能量轉換方式可分為動態能量轉換和靜態能量轉換。對于大功率空間核電源，靜態能量轉換效率低，提高功率輸出時將極大增加輻射散熱器的質量。動態能量轉換由于轉換效率高，輻射器面積相對較小，由太陽熱流引起的系統功率波動也極為有限。目前，動態能量轉換如斯特林循環、布雷頓循環等已成為大功率空間核反應堆設計采用的主要能量轉換方式。斯特林循環結合液態金屬冷卻反應堆可實現百千瓦級的功率輸出，如SP-100型空間反應堆系統設計方案[2]。

本文針對百千瓦級鋰冷快堆耦合斯特林循環的空間核電源系統，開發系統熱工水力分析程序，對特定事故工況進行安全分析，并為此類空間核電源的設計提供參考。

1 百千瓦級空間鋰冷電源

SP-100型空間核反應堆電源是美國最初為“星球大戰”(SDI)開發的軌道電源，任務可用軌道為2 000 km、傾角為28°的圓形軌道，而后也考慮將其作為星表能源，設計目標是提供100～1 000 kW功率輸出[3-7]。SP-100將主要部件及子系統模塊化，其反應堆和屏蔽散熱系統可與動態轉換裝置連接，滿足使用者的體積限制及功率水平[8]。

SP-100的斯特林動態轉換系統主要由堆芯、斯特林電機、電磁泵和熱管式輻射器組成[9]。系統由兩回路組成，一、二回路分別采用鋰(Li)和鈉鉀合金(NaK)作為冷卻工質。一回路Li工質經過堆芯加熱后與斯特林熱端換熱。斯特林機組采用冗余設計，以確保動力安全。

二回路NaK工質與斯特林冷端換熱后通過三級輻射器排放廢熱。熱管輻射器中，工質首先與鉀熱管蒸發段對流換熱，最終熱量通過與熱管冷凝段連接的C-C翅片輻射至宇宙空間。堆芯由燃料棒和安全棒組成，燃料棒芯塊采用氮化鈾(UN)。堆芯通用布置如圖1所示，可改變燃料組件數量實現不同等級的功率輸出。針對SP-100，大多研究集中于單一部件的分析建模[10]，對其系統整體建模研究以及瞬態分析較少。本文開發了可應用于大功率鋰冷快堆耦合斯特林電機的系統程序，以SP-100為對象進行建模仿真，研究其熱工安全特性。

圖1 SP-100堆芯通用布置Fig.1 SP-100 core general layout

2 數學物理模型

圖2 堆芯區域劃分示意圖Fig.2 Schematic of core area division

系統由堆芯、管道、斯特林發電機以及熱管輻射器組成。為簡化計算，堆芯沿徑向劃分分區，各分區計算1個平均通道(圖2)，忽略各分區之間換熱。通道由冷卻劑、芯塊、反射層及氣腔組成，沿軸向劃分控制體。忽略芯塊軸向導熱，考慮反應性反饋。對各部件控制體建立微分方程，求解采用改進吉爾算法，對斯特林模型采用四階龍格庫塔公式求解。

2.1 堆芯物理熱工模型

堆芯的功率瞬變計算采用點堆中子動力學方程[11]。考慮各通道流量以及燃料元件功率各不相同，采用并聯多通道模型，每個通道代表中子物理特性、熱工水力特性相似的一類元件。

對于燃料元件，考慮內熱源、芯塊導熱，能量方程如下：

(1)

對于氣隙及包殼，能量方程如下：

(2)

式中：ρ為密度，kg·m-3；c為比熱容，J·kg-1·K-1；T為溫度，K；λ為熱導率，W·m-1·K-1；r為徑向坐標，m；q為內熱源，W·m-3；t為時間，s-1；下標u表示燃料芯塊。

對于各通道內液態金屬工質，將其簡化為一維不可壓縮流動換熱模型，方程組如下。

質量方程：

(3)

動量方程：

(4)

能量方程：

(5)

式中：z為軸向坐標，m；W為質量流量，kg·s-1；A為通道流通面積，m2；f為摩擦阻力系數；De為通道水力直徑，m；h為冷卻劑對應比焓，kJ·kg-1；q為熱流密度，kJ·m-2；U為加熱周長，m。

2.2 斯特林發電機模型

斯特林發電機模型包括冷熱端壁面、氣體工質、回熱器等部分。對于氣體工質采用理想氣體絕熱微分方程組進行計算。斯特林冷熱端壁面有如下熱平衡方程：

(6)

(7)

式中：ρIn、ρOut分別為熱、冷端包殼材料密度，kg·m-3；TIn、TOut分別為熱、冷端包殼內壁溫度，K；Tf為氣體溫度，K；AIn、AOut分別為熱、冷端截面面積，m2；λIn、λOut分別為熱、冷端材料熱導率，W·m-1·K-1；δIn、δOut分別為熱、冷端包殼壁面厚度，m；cIn、cOut分別為熱、冷端包殼材料比熱容，J·kg-1·K-1；ΠIn、ΠOut分別為熱、冷端換熱周長，m；TH為熱源溫度，K；TC為熱阱溫度，K；Hf為氣體與壁面的換熱系數，W·m-2·K-1；ηST為斯特林效率。

加熱器、冷卻器與回熱器為有限溫差傳熱，具有相似控制方程，循環換熱量如下：

Qi=hiAw,i(Tw,i-Tg,i)(1/n)

(8)

式中：Q為循環換熱量，W；h為工質與壁面換熱系數；Tw為內壁面溫度，K；Tg為氣體溫度，K；n為機軸轉數；i為所劃分的控制體編號。

實際回熱器有回熱損失，定義有效度ε，ε為實際循環回熱量與理想循環回熱量之比。忽略回熱器導熱熱阻，有：

(9)

式中：Awg為換熱面積，m2；A為工質自由流動面積，m2；St為斯坦頓數，對于工質氦氣，St=0.46Re-0.4Pr-1。

回熱器軸向熱損失Qloss可由下式計算：

(10)

式中：λr為回熱器外殼處熱導率，W·m-1·K-1；Ar為回熱器橫截面積，m2；lr為回熱器長度，m；Th、Tc分別為熱、冷側平均溫度，K。

2.3 輻射散熱器模型

輻射散熱器模型分為回路管網模型及熱管輻射單元模型。管網結構如圖3所示，管網模型中假設流體不可壓縮，忽略散熱。

圖3 回路式輻射器管網結構Fig.3 Pipe network structure of loop radiator

根據守恒關系可得如下方程：

(11)

(12)

(13)

圖4給出典型輻射單元結構。輻射單元由熱管及焊接在熱管上的翅片組成，排出熱量有3部分：翅片兩側輻射換熱(Q1)，熱管翅片散熱(Q2)，裸露的熱管散熱(Q3)。

圖4 輻射單元示意圖Fig.4 Schematic of radiator unit

熱管模型包括管壁導熱、吸液芯內工質流動傳熱、蒸汽流動3部分。忽略吸液芯流動影響，采用純導熱模型求解吸液芯及管壁區域，假設蒸汽區域溫度均勻。

管壁區域控制方程如下：

(14)

吸液芯區域控制方程如下：

(15)

(16)

式中：C為體積熱容，J·m-3·K-1；x為徑向坐標，m；K為導熱系數，W·m-1·K-1；y為軸向坐標，m；下標w及ws分別表示管壁及吸液芯，eff指折算后的吸液芯參數，l及s分別表示工質及吸液芯。

翅片模型參考文獻[12]。

3 結果與分析

RE-1000為美國Sunpower公司為NASA設計的1 kW原型樣機[13]，利用RE-1000的實驗結果對斯特林模型進行驗證。RE-1000的主要參數參考文獻[14]。表1列出計算結果與實驗數據對比，最大相對誤差為17.1%。由表1可見，該模型可準確分析斯特林模型的性能。

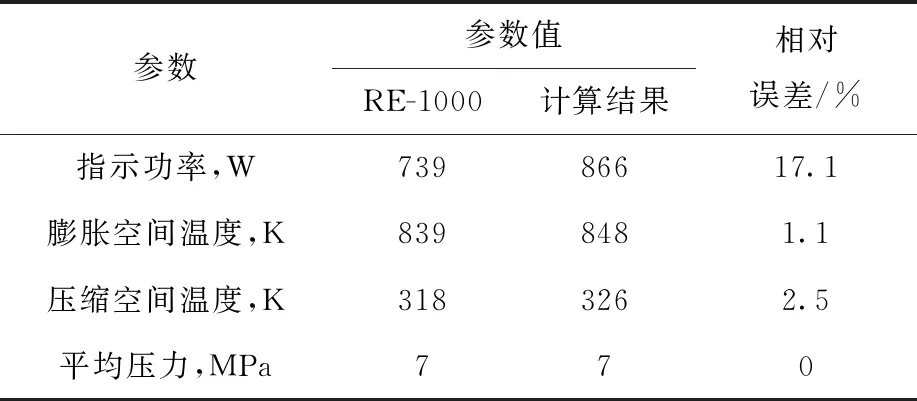
表1 參數模型計算結果與實驗數據對比Table 1 Parameter comparison of model calculation result with experimental data

3.1 穩態結果分析

根據文獻[7]給出的堆芯及輻射器進出口溫度設計值，考慮堆芯在實際熱功率輸出為455 kW時，系統穩態計算結果列于表2，計算值與設計值誤差較小，并將作為后續瞬態計算的初始條件。

3.2 事故工況分析

1) 反應性引入事故

本計算中，1 s內向堆芯引入0.1 $反應性，保護系統不動作。圖5示出堆芯及斯特林功率瞬態響應特性，堆芯功率在200 s內迅速升高至880 kW。由于功率升高引起堆芯溫度升高(圖6)，整體的負反應性反饋(圖7)使得堆芯功率逐漸下降(圖5)，最終穩定在470 kW，斯特林功率也逐漸升高至穩定。由于堆芯功率的劇烈升高，熱點溫度迅速升高，200 s內增加約110 K，并未超過芯塊熔點3 120 K[15]，具有較大的安全裕度。

表2 穩態計算結果Table 2 Steady state result

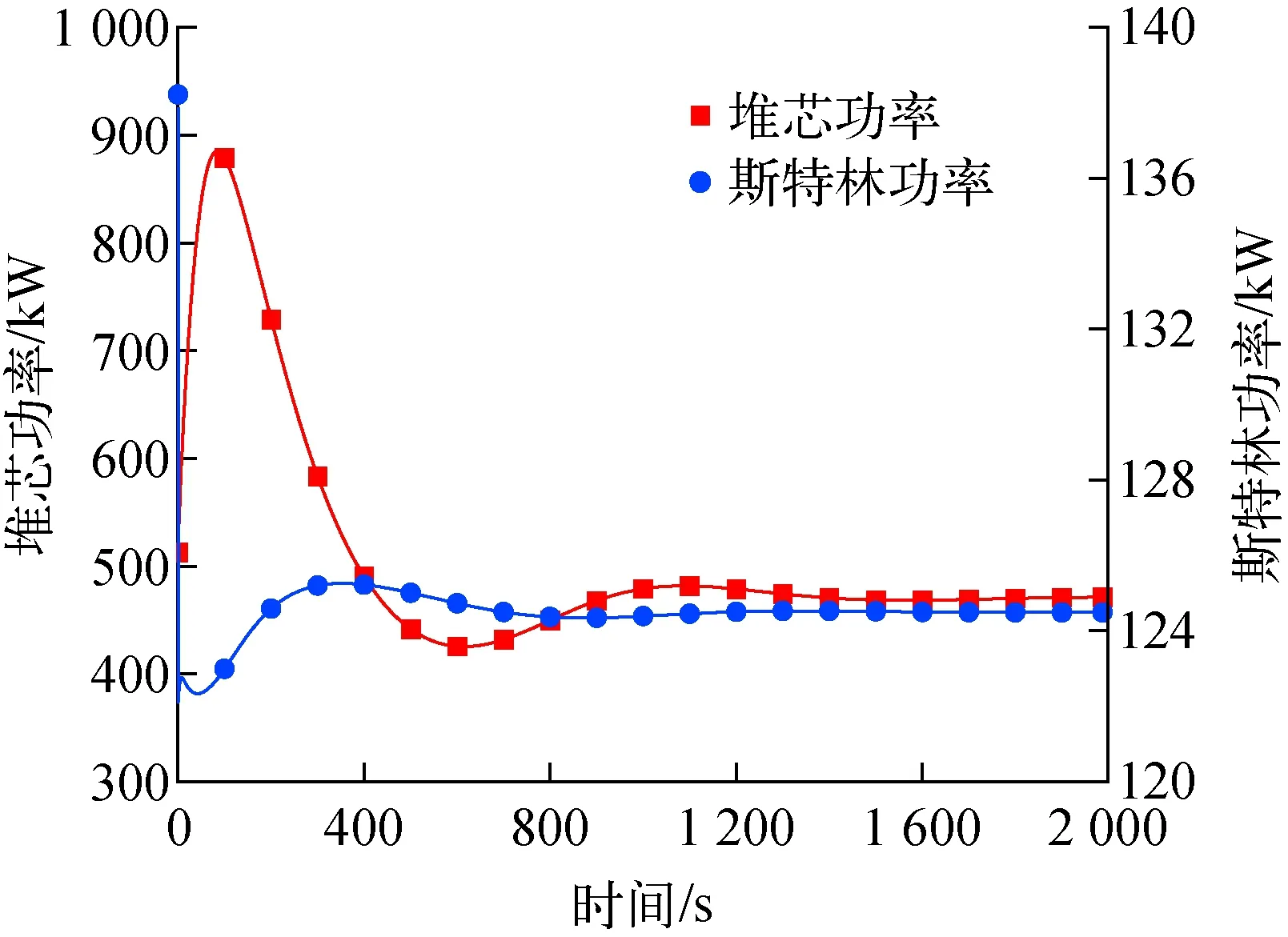
圖5 反應性引入事故下斯特林及堆芯功率的變化Fig.5 Change of Stirling and core power under reactivity insertion accident

對于二回路，堆芯額外正反應性的引入導致對熱量排出能力的要求提高，輻射器平均溫度迅速上升(圖8)，排出多余熱量為一回路提供足夠冷卻。雖然系統特性可將堆芯熱量有效移除，但額外反應性引入導致堆芯熱點溫度迅速上升，對于更高的反應性引入，可能產生冷卻劑局部沸騰，因此仍需額外防護以減少此類事故的發生。

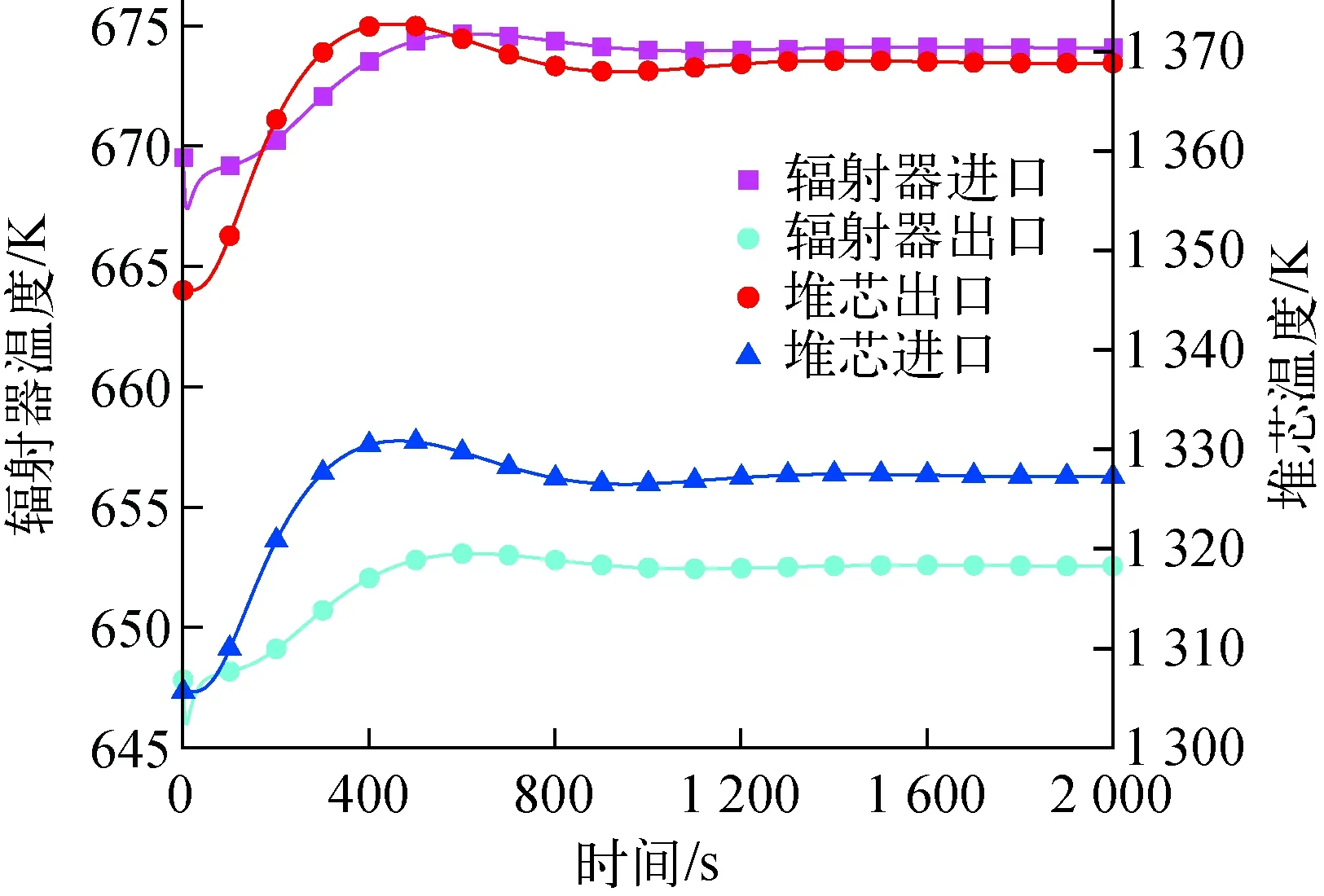
圖6 反應性引入事故下輻射器及堆芯進出口流體溫度的變化Fig.6 Fluid temperature change of radiator and core inlet and outlet under reactivity insertion accident

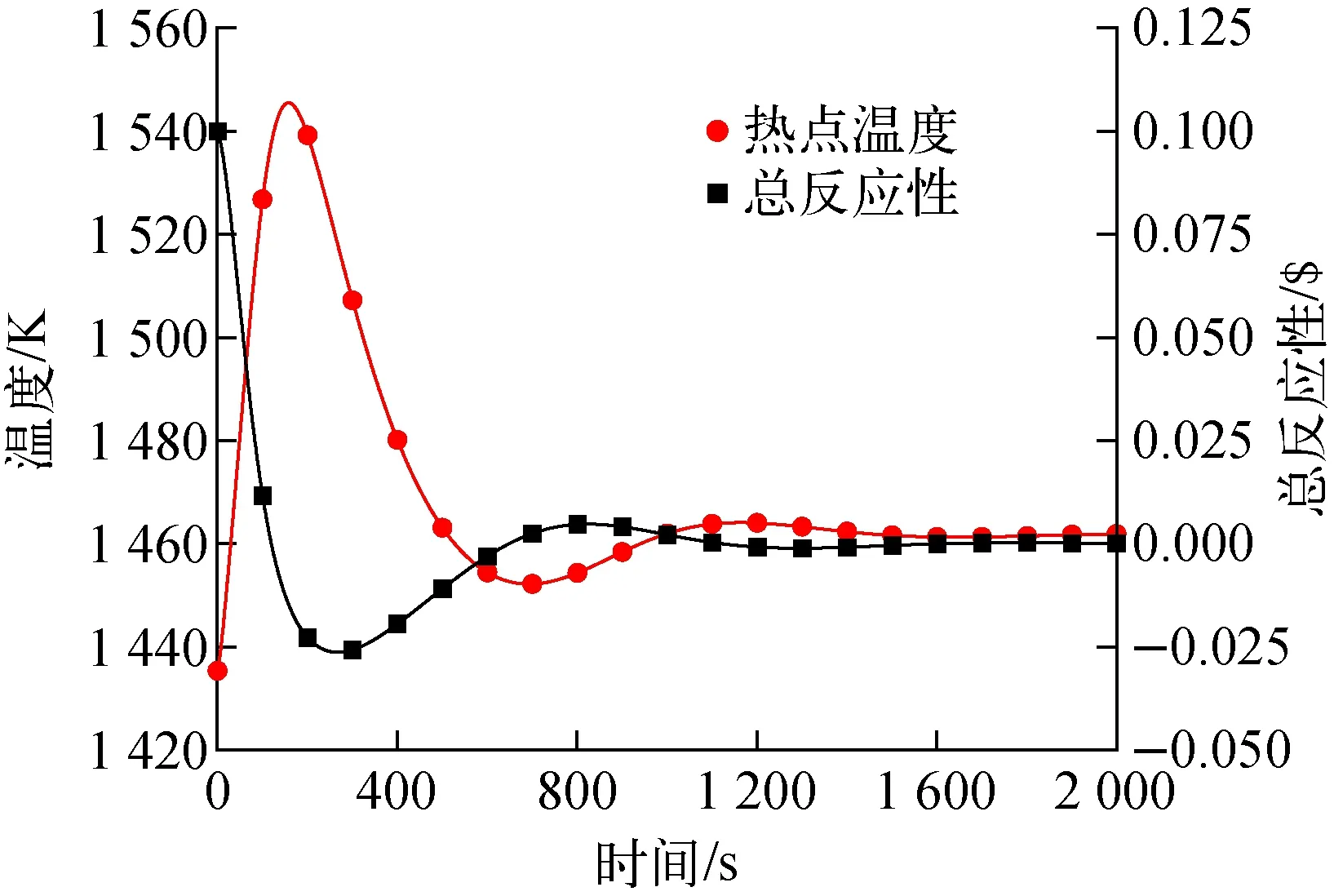
圖7 反應性引入事故下熱點溫度及堆芯總反應性變化Fig.7 Change of hot point temperature and total core reactivity under reactivity insertion accident

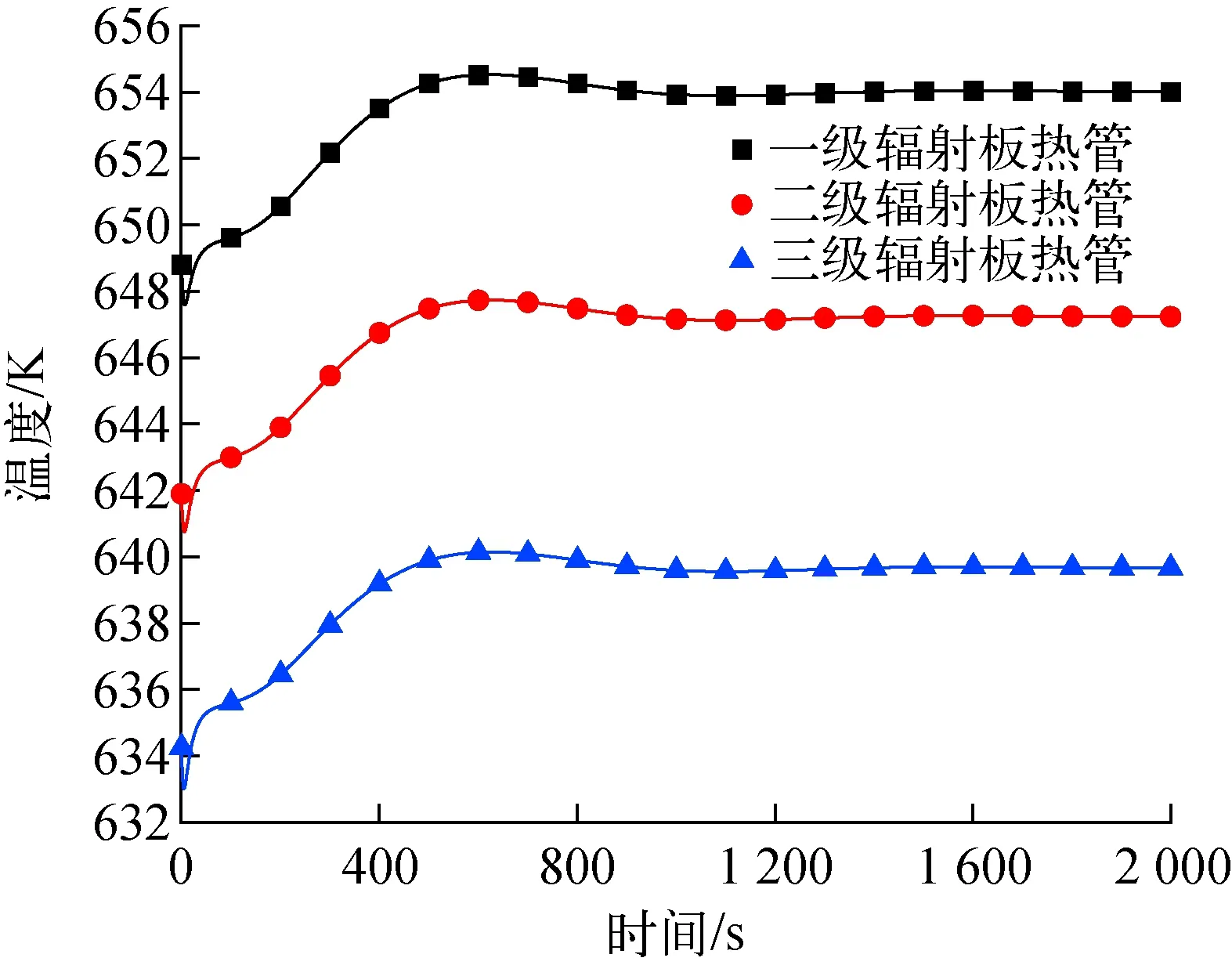
圖8 反應性引入事故下輻射器熱管冷凝段溫度的變化Fig.8 Temperature change in condensation section of radiator heat pipe under reactivity insertion accident

2) 熱阱喪失事故

若二回路輻射器發生部分熱管失效，將導致系統熱阱喪失。計算中考慮30%的熱管破裂失效，系統無保護動作。

熱點溫度的變化與反應性變化趨勢一致，如圖9所示。受到二回路熱阱喪失影響，一回路平均溫度升高，燃料元件及堆內結構的負反應性反饋使得總體反應性下降，最低可降至-0.005 $，反應堆及斯特林功率也隨之下降(圖10)。最終，總反應性與堆芯功率逐漸震蕩至穩定，堆芯功率穩定在410 kW。

圖10 熱阱喪失事故下斯特林及堆芯功率變化Fig.10 Change of Stirling and core power under loss of heat sink accident

圖11示出輻射器及堆芯進出口溫度的瞬態響應特性。事故發生前期，二回路側溫度迅速升高。輻射器進出口溫度迅速增加，約在450 s后達到穩定，平均溫度增加約50 K。在部分熱管破裂后，其余部分熱管溫度升高(圖12)，承擔多余的熱量排出，體現了系統安全特性。

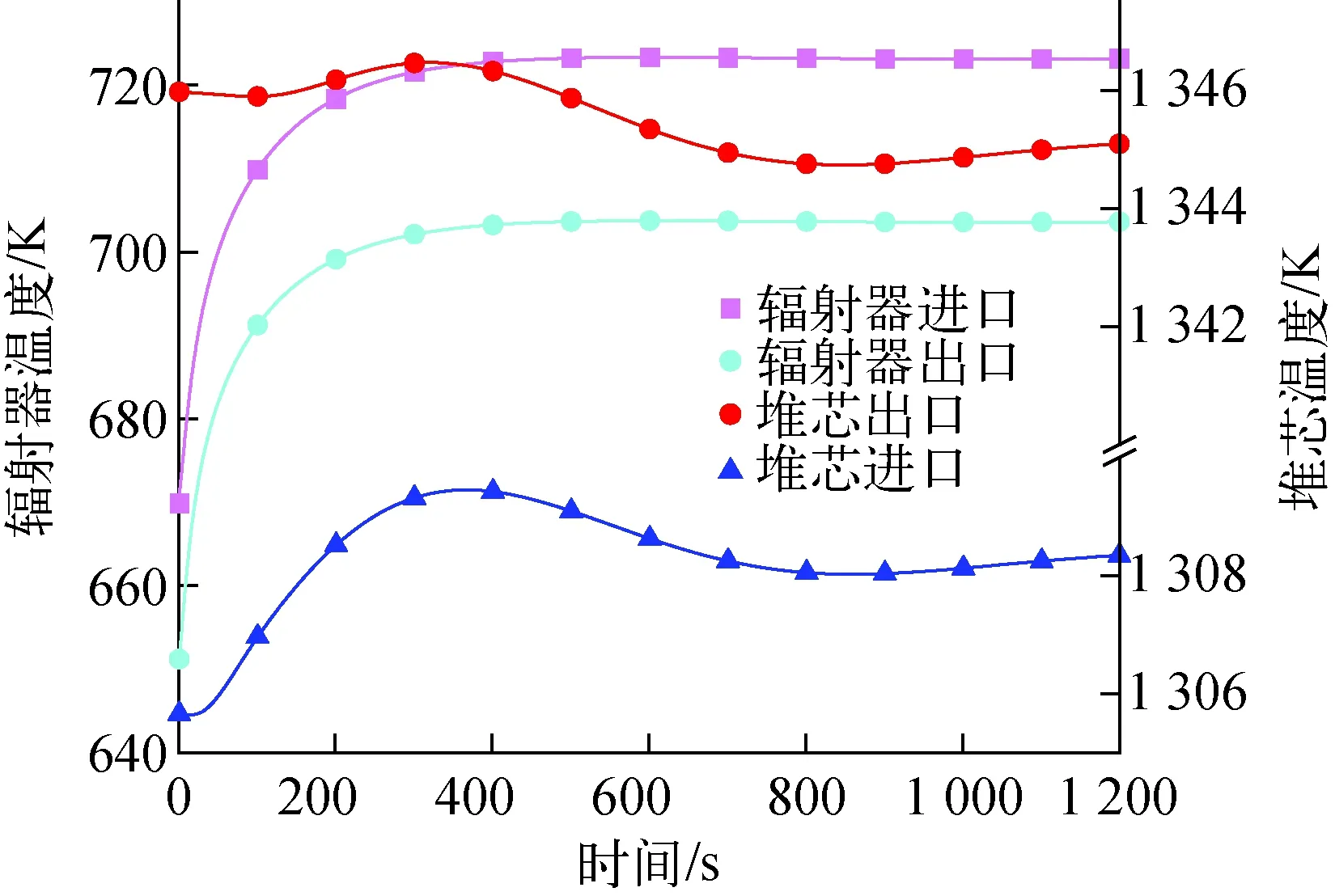
圖11 熱阱喪失事故下輻射器及堆芯進出口流體溫度變化Fig.11 Fluid temperature change of radiator and core inlet and outlet under loss of heat sink accident

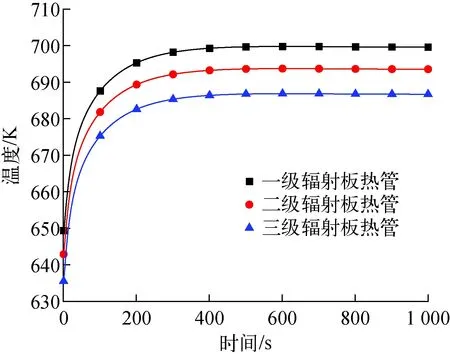
圖12 熱阱喪失事故下輻射器熱管冷凝段溫度變化Fig.12 Temperature change in condensation section of radiator heat pipe under loss of heat sink accident

整體來看，事故發生時一回路溫度有一定上升趨勢，出口溫度變化相對于進口溫度有一定延遲(圖11)，堆芯總體反應性受溫度負反饋效應的影響，導致堆芯功率及熱點溫度降低，熱點溫度最低降至約1 423 K。因此部分熱阱喪失且無額外保護動作時，系統仍可維持正常運行，具有較高的安全特性。

4 總結

本文針對百千瓦級鋰冷快堆空間核電源系統建立數學模型，并對SP-100進行了模擬仿真，得到如下結論。

1) 本文開發了空間鋰冷快堆瞬態熱工分析程序，利用RE-1000實驗數據對斯特林模塊進行校核，最大相對誤差為17.3%，驗證了模型的合理性。利用所開發程序針對采用斯特林循環的SP-100進行建模，進行了反應性引入事故及熱阱喪失事故的計算。

2) 熱阱喪失事故中，由于熱管的固有安全性以及堆芯負反應性反饋的影響，可在事故發生時有效排除熱量，降低堆芯功率，維持系統的正常運行，體現出系統安全特性。在反應性引入事故中，熱點溫度迅速升高，低于安全限值并有極大安全裕度。但仍需防止此類事故的發生，熱點溫度的急劇上升可能產生局部沸騰。

本文結果證明了所開發程序可準確分析大功率鋰冷快堆空間核電源系統的熱工安全特性，為此類系統設計優化奠定理論基礎。對于更高反應性引入，可能導致鋰冷卻劑出現局部沸騰，此類事故分析將在后續工作中繼續進行。