基于線控電子液壓制動系統的車輛減速度控制

唐派，熊璐，李軍，舒強，冷搏

(1.重慶交通大學機電與車輛工程學院， 重慶 400074;2.上海同馭汽車科技有限公司， 上海 201800;3.同濟大學汽車學院，上海 201804)

0 引言

隨著當前車輛的電動化、智能化發展不斷加深，毫無疑問對車輛行業提出了更高的要求。對于我國汽車行業而言機遇和挑戰并存，在眾多難點中制動系統的電動化轉變至關重要。

傳統車輛使用真空助力器提供制動助力，但是新能源車型沒有能夠直接提供真空度的發動機,所以需要額外的真空泵、儲氣罐等設備,此方案存在工作噪聲大的問題影響整車舒適性。并且在制動能量回收方案設計上，真空助力器方案只能在液壓制動上疊加電助力，降低了制動能量回收率，同時存在著影響駕駛員制動踏板感的問題。

此外,自動緊急制動(autonomous emergency braking,AEB)、自適應巡航控制(automatic cruise control,ACC)等各類高級駕駛輔助功能(advanced driver assistant system,ADAS)也對車輛縱橫向控制性能提出了更高的要求。傳統制動系統采用真空源提供制動助力的方案存在連續建壓能力不足的缺點。同時線控建壓響應較難滿足緊急制動的響應時間要求。

基于傳統執行器開展的減速度控制研究較少，多數利用高壓蓄能器的主動建壓能力實現AEB功能。馬國成等基于ESC執行機構，以減速度作為控制目標，對液壓力進行控制。根據電磁閥開閉的非線性特性，基于分段設計的思想在不同特性下采用不同的PID參數以期實現對壓力的準確控制。但重點在壓力控制部分，車輛減速度控制并未過多體現。

當前也有部分學者基于線控制動系統開展減速度控制研究。張東利用相關執行器，根據行車過程中自車與前車安全距離作為控制目標，設計AEB觸發時機。但是僅設計了緊急制動工況的減速度控制，缺乏對減速度控制精度、超調特性、響應時間的研究，也沒有考慮道路坡度因素對減速度控制的影響。

為了盡量消除道路縱向坡度對于車輛動力學控制的擾動，雍文亮等利用車輛動力學和加速度傳感器兩個信息源，采用基于Kalman濾波器的融合算法對道路坡度進行估計。

綜上所述，當前學者對于新型制動系統的研究重點集中于壓力控制。此外，在設計用于整車減速度控制的動力學模型時，并未考慮坡度因素對減速度控制的影響。鑒于此，文中基于EHB優異的液壓控制性能，設計考慮道路坡度因素的減速度控制模型,并采用模糊PID控制方法提升了減速度控制魯棒性。

1 線控電子液壓制動系統介紹

線控電子液壓制動(electro-hydraulic braking,EHB)系統由電機、控制器、減速機構、制動主缸等部件組成，如圖1所示。電機扭矩經過蝸輪蝸桿、齒輪齒條傳動副實現減速增扭,并且將電機的轉動轉化為齒條的平動,從而推動主缸活塞完成建壓。

圖1 EHB總成

EHB使用機械解耦的方案，駕駛員通過制動踏板輸入-液壓力輸出關系解耦，可以實現更高自由度的制動能力回收的同時保持整車減速度。同時，利用踏板感覺模擬器使得駕駛員制動腳感與傳統真空助力器制動腳感保持一致。

當前量產車型的各類高級駕駛輔助系統功能多使用車身穩定控制系統作為線控液壓執行器。由于ESP主動建壓依靠柱塞泵，而EHB通過永磁同步電機建壓，在建壓速度、最大建壓能力、最大保壓時間、循環使用壽命等方面的關鍵指標均優于ESP。EHB與ESP建壓性能對比見表1。

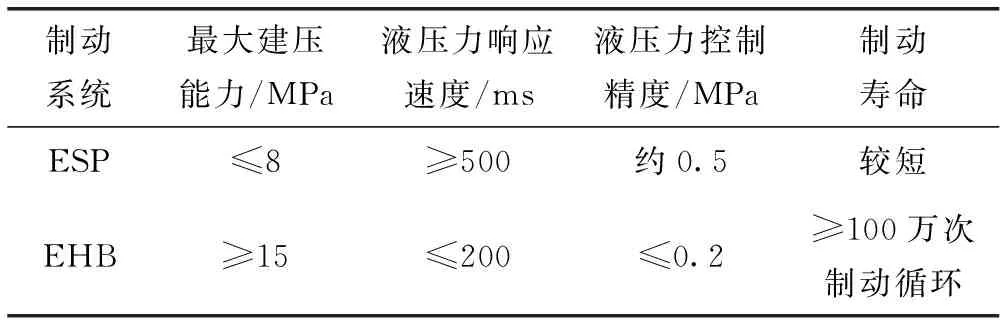
表1 EHB與ESP建壓性能對比

2 車輛動力學建模

本文所建立的車輛縱向制動減速度控制策略如圖2所示。

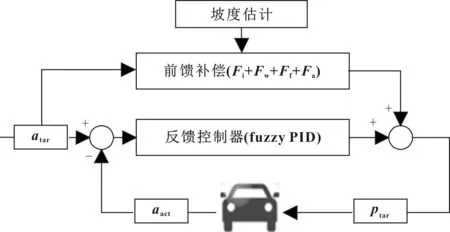
圖2 減速度控制策略

圖中：為坡度阻力;為空氣阻力;為滾動阻力;為加速阻力;為目標減速度;為實際加速度;為目標液壓力。

汽車行駛驅動力-阻力平衡方程為:

=+++;

(1)

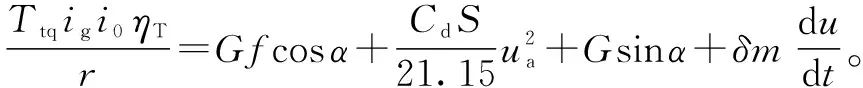
(2)

式中：為驅動力；為發動機輸出扭矩；為變速器傳動比；為減速器傳動比；為機械效率；為重力；為道路坡度；為空氣阻力系數；為迎風面積；為車速;為旋轉質量等效系數;為車輛質量。

以下對道路阻力、制動器模型以及EHB建壓特性進行分析。

2.1 車輛道路阻力求解

實車測試中，空氣阻力和滾動阻力可以通過實測空擋滑行測試直接求解。使用表示此兩項的值，則=+。通過在不同初始車速下掛入N擋滑行，得到道路阻力MAP，如圖3所示。

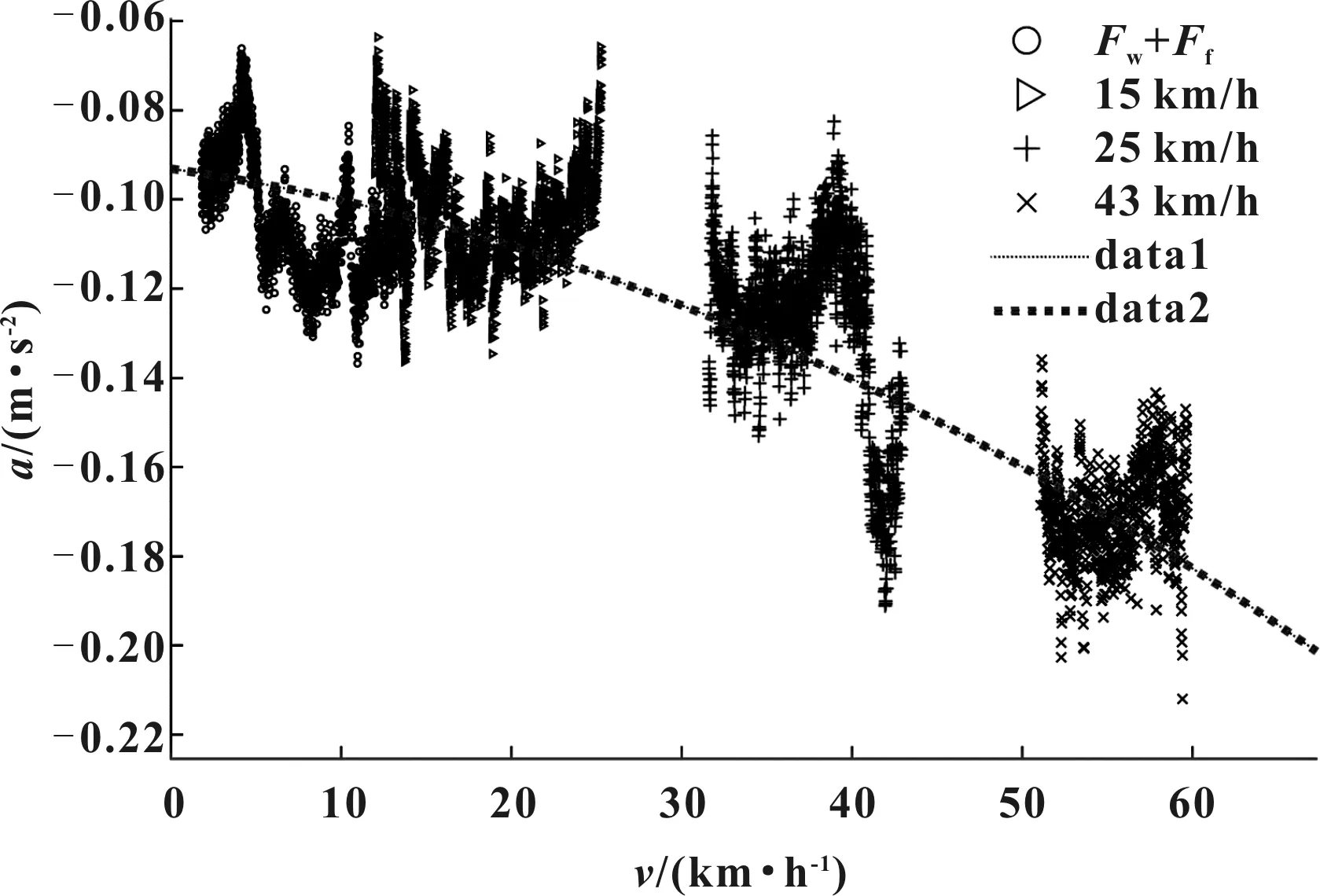
圖3 道路阻力MAP

擬合方程為：

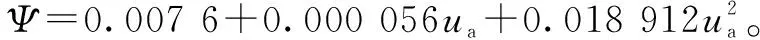
(3)

2.2 制動器建模

試驗車輛基礎制動器部分參數見表2。

表2 制動器部分參數

根據以上參數利用式(3)可以計算出制動扭矩

=2π4。

(4)

式中：為制動力矩；為摩擦因數；為系統液壓力；為輪缸直徑；為輪缸數量；為制動半徑。

通過計算，同時采用實際測試的方法進行驗證：以60 km/h初速度建壓，施加固定液壓制動到車速為零，從0.5 MPa開始每間隔0.5 MPa測試1次，每組測試3次。減去所求解的道路阻力產生的減速度，求解得到液壓力-減速度的對應關系，如圖4所示。

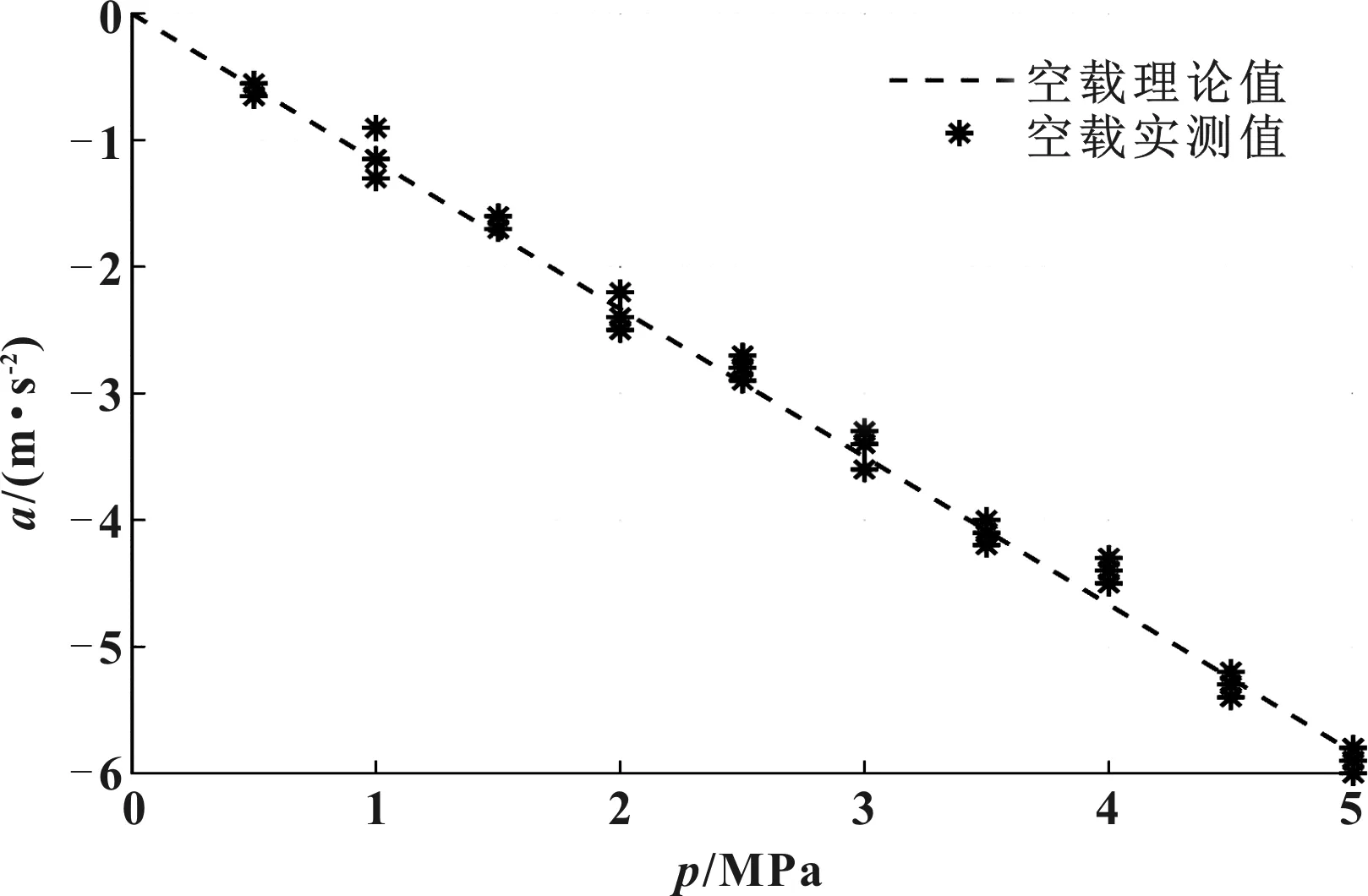
圖4 液壓力-減速度的對應關系

由圖4可知，實際測試結果和理論計算結果是一致的，驗證了試驗結果的可靠性。

2.3 EHB液壓力控制性能分析

在各種液壓力控制工況中，階躍響應是對EHB液壓力控制性能要求最為嚴格的工況，在要求響應時間的同時，不允許系統存在過大超調。但圖5中高液壓階躍響應下存在的“超調”是由于管路節流特性所決定，并非真實系統超調。

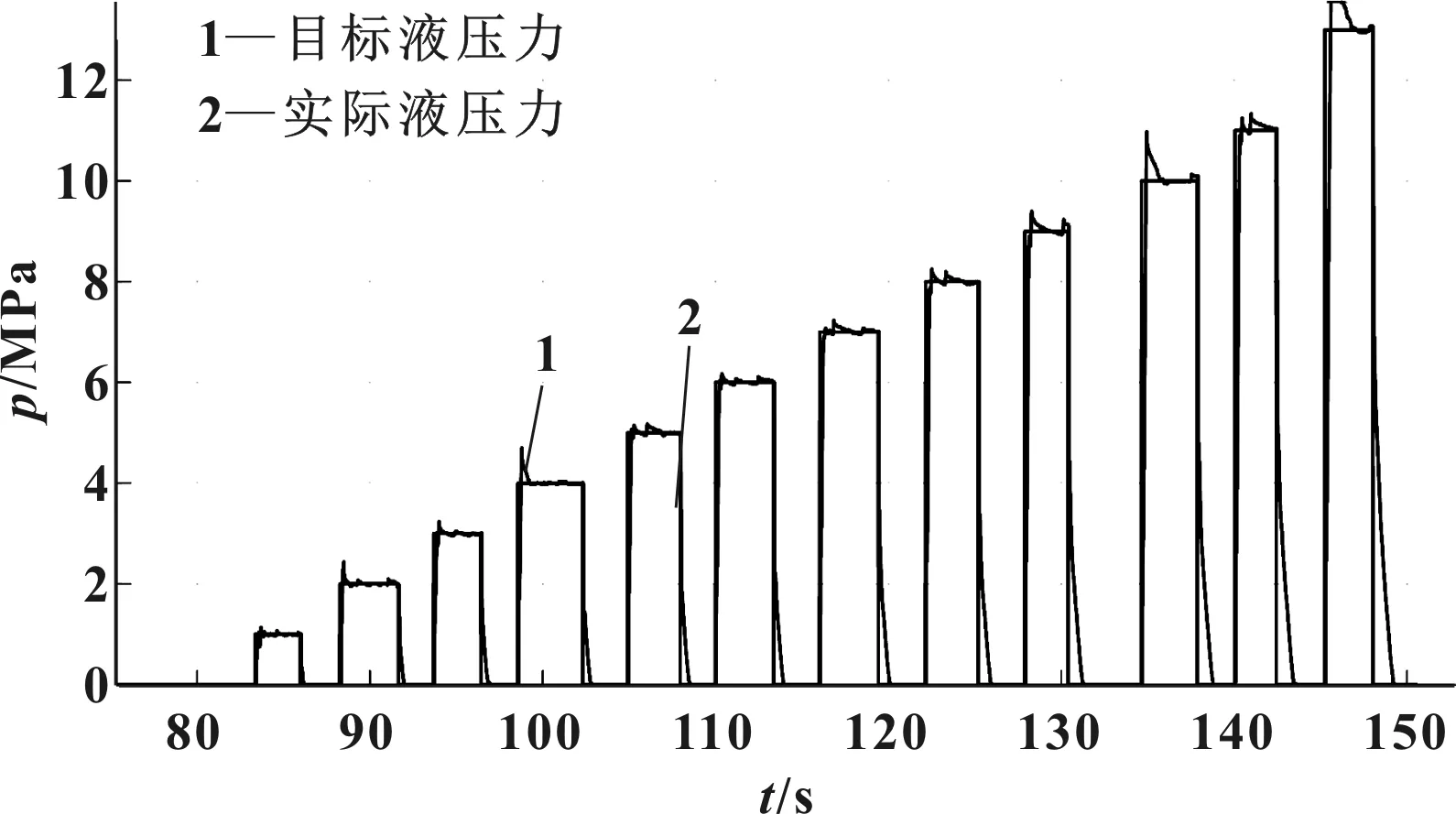
圖5 EHB線控階躍液壓測試

測試結果表明，EHB階躍液壓力10 MPa下響應時間小于200 ms。在階躍測試下通過參數辨識將液壓力控制系統認為是二階系統，求得EHB建壓性能傳遞函數為：

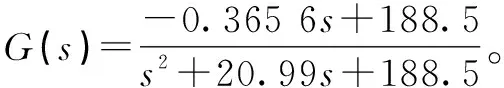
(5)

2.4 仿真與實測結果對比

采用液壓力開環測試，給定單位階躍目標液壓，測試整車減速度響應。實際測試中記錄加速度傳感器信號，并且使用輪速信號差分求解輪減速度，利用Garsim得到仿真和實際測試對比結果，如圖6所示。

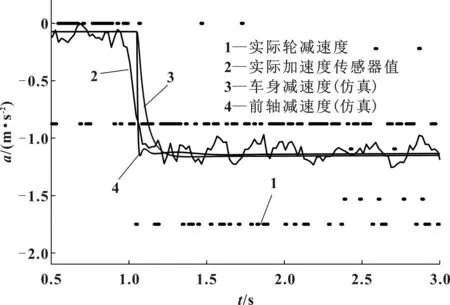
圖6 階躍減速度仿真實測對比

由圖6可知，受總線通信速率以及傳感器精度影響，實際計算的輪減速度誤差較大，在穩態情況下存在1 m/s的誤差。通過對比Carsim模型仿真結果和真實測試結果，可以確認所建立的車輛動力學模型的準確性。

3 基于Kalman的坡度估計

坡度會在很大程度上影響減速度控制精度，有必要對此進行估計。當系統為線性系統，并且噪聲具有獨立性時，可以使用Kalman進行參數估計。

離散Kalman公式如下：

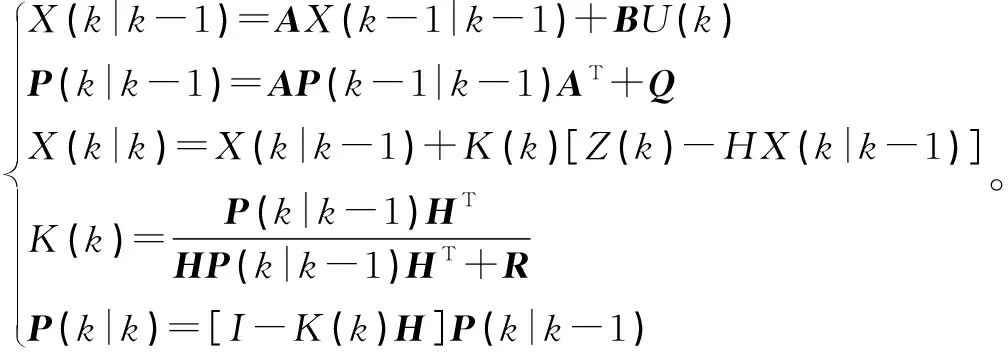
(6)

式中：(|-1)為先驗估計值；為狀態轉移矩陣；(-1|-1)為上一時刻最優估計；為控制矩陣；()為系統控制參數；(|-1)為協方差矩陣;(-1|-1)為協方差矩陣更新；為系統建模誤差；為觀測誤差；()為Kalman增益；()為系統觀測參數；為系統觀測矩陣。

利用加速度傳感器信號原理可知，得到車輛實際加速度后便可以獲得坡度信息：

=+sin。

(7)

由此建立Kalman過程方程(8)和觀測方程(9)：

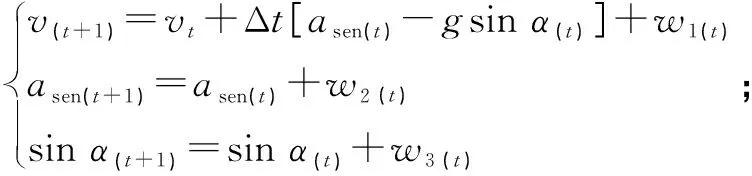
(8)

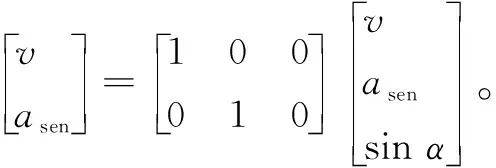
(9)

根據真實傳感器模型構建和矩陣分別為：

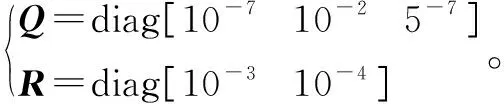
(10)

與一階低通濾波器進行坡度計算的結果進行對比，低通濾波器計算公式為：

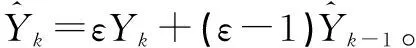
(11)

圖7為坡度估計結果對比，其中Raw值為原始數據直接求得的結果。為方便觀測，選取縱坐標為gsin,即重力在坡道方向的分量，表示坡度。

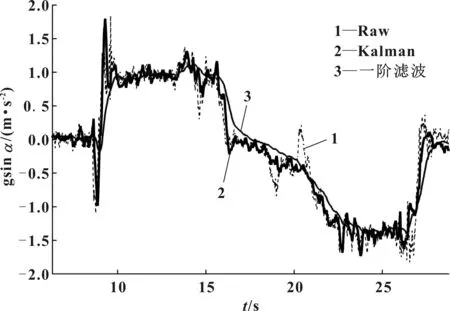
圖7 坡度估計結果對比

由圖7可以看出，使用基于Kalman的坡度估計方法在保證坡度估計準確性的情況下，相比于采用一階濾波方法，可以提高響應速度。由曲線1可以看出，采用傳統一階濾波方法，必須采取極高的截止頻率才能過濾掉此類噪聲，但會引入較大的延遲。

4 減速度閉環控制方法

傳統PID控制方法計算公式為：

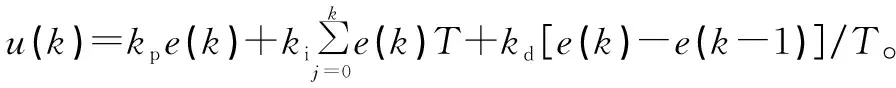
(12)

式中:為比例系數；為微分系數；為積分系數；為采樣周期;()為誤差;為積分周期值。

采用傳統控制方法無法滿足車輛在不同目標減速度下響應的一致性要求，由此文中采用模糊PID控制方法。模糊控制將輸入量模糊化，通過已知特性得到的經驗規則計算得到模糊化的輸出量，最終通過求解模糊方程得到精確的控制輸出量。

使用減速度控制量()=-和減速度變化率Δ()=()Δ作為模糊控制器的輸入,求解目標液壓力。

根據實車標定測試，確定()為：

[-0.2 -0.5 -1 -2 -3 -4 -5]。

Δ()范圍為：

[-15 -10 -5 -3 0 3 5 10 15]。

兩者的模糊域都設置為[]，構建模糊控制規則，最終轉化為MAP圖，如圖8所示。

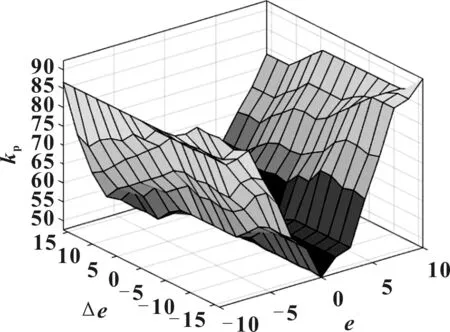
圖8 模糊PID MAP圖

仿真試驗驗證采用階躍減速度測試，結果如圖9和圖10所示。

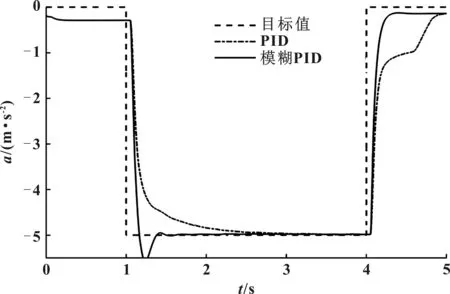
圖9 PID-模糊PID減速度控制對比

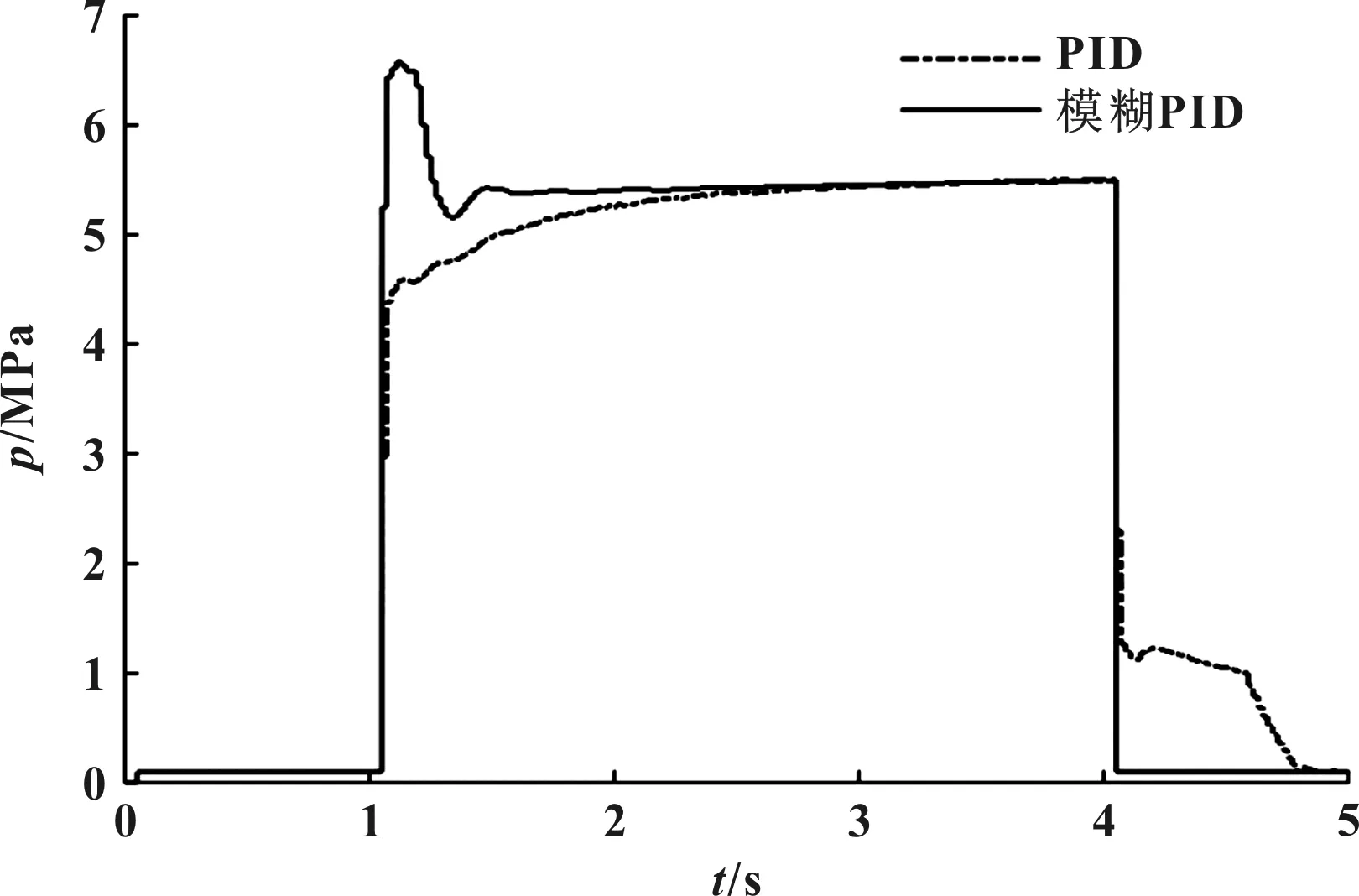
圖10 PID-模糊PID液壓控制對比

由圖可以看出采用模糊PID后，在對于響應要求更為嚴苛的階躍減速度測試下，由于模糊PID能夠有效利用反饋信息，所以使得減速度響應時間得到有效提升。PID-模糊PID性能對比結果見表3。

表3 PID-模糊PID性能對比

5 結語

文中基于EHB優異的液壓力控制性能，設計了用于車輛減速度控制的車輛動力學模型。并且在PID控制基礎上，設計了適用不同減速度控制工況下的模糊PID控制器，得出了以下結論：

(1)基于理論和實際測試互相參考，對車輛行駛過程中的道路阻力進行了精確的計算，并通過了試驗驗證。

(2)利用Kalman進行道路坡度估計降低了坡度估計的延遲。

(3)采用模糊PID的控制方法，相比于傳統PID控制方法，提高了減速度控制的響應時間。