帶有深度學習的多特征選擇組合算法燃氣輪機參數建模

張寶凱

(中國大唐集團科學技術研究總院有限公司華東電力試驗研究院，合肥 230031)

煤炭發電以低廉的經濟成本占據著我國能源結構的主要部分，發電過程中釋放的NOx污染物危害自然社會系統。與煤炭發電相比，燃氣-蒸汽聯合循環電廠以天然氣為燃料，發電產物清潔，NOx排放濃度僅為煤炭電廠的1/10[1]。

燃氣輪機NOx排放濃度能夠間接反映機組的燃燒健康水平，是建立燃燒調整模型的重要變量[2]。異常的排放特性影響機組的燃燒效率，使燃燒脈動不穩定，觸發負荷超馳機制。準確地預測NOx可以對異常工況進行預警，消除安全隱患。

構造預測模型的第一個關鍵步驟是針對研究問題找到適合的建模方法。在已有研究中，建模方法以機理方法[3]、統計學方法[4]和數據驅動的智能方法[5]為主要三類。趙雄飛等[6]結合統計學方法得到了燃氣輪機數學建模特性方程最佳擬合次數，確定了擬合曲線，減小了與對象實際曲線運動規律間的建模誤差。曹軍等[7]利用APROS軟件對燃氣輪機熱力過程進行質量、動量分析，遵循能量守恒法則對F級燃氣-蒸汽聯合循環機組全范圍過程進行實時動態仿真。然而，以上方法在建模精度方面都有提升空間。廠級數據監控系統(supervisory information system，SIS)作為智慧電廠建設平臺實現了過程控制中大量參數數據狀態的監測記錄與實時訪問，為數據驅動智能建模控制策略提供了技術支持[8]。李景軒等[9]設計了一種以智能算法作為機理模型誤差補償的混合模型控制器方法，并對不同組合方式的設計進行了基于分布式控制系統(distributed control system，DCS)數據的驗證實驗，提高預測精度。liu等[10]將基于正交試驗的模糊優化方法應用于傳感器建模過程中，提高了傳感器建模效率與傳感器精度。以上研究在參數建模方面取得了成功，然而均為淺層機器學習方法，不能夠捕捉數據底層的深層次有用信息且建模精度有提升空間。

構造預測模型的另一關鍵步驟是找出更能解釋內生變量非線性邏輯關系的代表性解釋變量。燃氣輪機變量建模過程中極強的關聯性增加了模型的學習時間，產生的共線性問題也會使模型精度不高。與之相反，缺失變量則會泛化模型的解釋性。因此，通過對解釋變量進行特征約簡，剔除與內生變量不相關、弱關聯以及冗余的建模解釋變量可以整體改進預測模型的魯棒性、精度及學習速度。Zhang等[11]基于偏互信息(partial mutual information,PMI)算法解決了解釋變量間的關聯關系對建模精度的影響，在選擇出的最佳輸入量集的基礎上構建有效高精度預測模型。該方法在極短時間內，憑借對自身數據的度量規則處理大量高維維數下的無關特征，且算法在進行選擇特征時獨立于后續學習器，計算效率大大增強。Zhang等[12]針對LASSO算法在變量選擇時沒有將協變量之間的相互作用考慮在內，設計出一種利用特征超圖與多維互動信息技術相融合的新正則化項，通過約束有效評估特征特性。吳笑研等[13]對煤電鍋爐效率相關生產數據進行CART分析，選擇出重要性高于5%的動態建模特征，滿足了鍋爐燃燒控制生產運行需求精度的要求。二種嵌入式方法在特征選擇時可認為是將算法與學習器一同作為優化整體，參與學習訓練過程，挖掘了數據結構中的內在相關性，檢測數據冗余。以上研究在特征選擇方面效果表現突出，憑借自身算法特性均能實現對變量特征的選取。

與已有研究構建模型時輸入特征采用單一、分步特征選擇[14]方法的淺層機器學習機模型不同，本文設計了一種基于深度置信網絡非線性組合多特征選擇方法，具體工作在于三個方面：(1)結合專家機理分析CART、PMI、LASSO算法，對NOx預測模型的輸入參數進行選取；(2)采用深度DBN網絡對建模參數進行建模；(3)采用DNN算法對不同特征選擇下的預測模型進行非線性組合，得到最終MFNDBN預測模型，并且設計實驗驗證所提出算法的有效性。

1 聯合循環系統分析

燃氣-蒸汽聯合循環系統主要由燃氣輪機、余熱鍋爐以及汽輪機間相互協調，快速響應電網AGC控制，并且由于占地體積小、機組啟停快、發電效率高以及CO2、SO2、NOx排放量少而逐漸被關注。工作狀態下，空氣經前置過濾器后由進口導葉IGV進入壓氣機形成壓縮的高壓空氣，并通過進氣加熱模塊IBH將空氣的預混燃燒范圍進一步擴大。天然氣通過前置站模塊將品質合格的天然氣經速比閥、燃料閥后以環管分布的噴嘴送入燃燒室與高壓空氣混合燃燒，膨脹的高壓高溫燃氣帶動透平葉輪經負荷齒輪箱將機械能傳遞給發電機，而尾端的高溫燃氣繼續進入余熱鍋爐，通過輻射換熱，將給水加熱至指標合格的工質驅動汽輪機缸體內動葉片，帶動發電機發電。圖1經燃燒室燃燒后的燃氣中含有的NOx濃度間接反映了機組其他關聯參數的運行狀態是否在合理的設計值范圍內，NOx參數建模為機組燃燒穩定與安全設計下的其他關鍵參數優化提供決策指導。

1—余熱鍋爐；2—壓氣機；3—燃燒室；4—透平；5—發電機；6—汽輪機；7—凝汽器；8—凝結水泵；9—負荷齒輪箱。圖1 燃氣-蒸汽聯合循環系統流程簡圖

2 基于深度置信網絡的多特征選擇算法NOx排放建模

2.1 數據預處理

離群點是一種在數據挖掘過程中偏離正常監測下的數據數值，它的產生均由突發事件下的內部機制變化、測量等錯誤行為而引發，會對模型預測增加難度。DBSCAN異常點檢測方法是一種可以利用數據特征分布密度程度不同而檢測離群點的高效聚類算法[15]，它不需要對簇的數量進行提前指定，而是通過密度來確定相似屬性簇。其中，算法將所有樣本點劃分為核心點、邊界點以及不同于前二者的異常點，核心點和邊界點被劃分在同一個簇中，而后者則在簇中心ε-領域(Epsilon)內。ε-領域計算如式(1)和式(2)所示：

Nε(Xj)={Xi∈D|dist(Xi,Xj)≤ε}

(1)

(2)

式中:dist(Xi,Xj)定義為馬氏距離；D∈{X1,X2,…,Xn}；ε為小的正數；Nε(Xj)代表與個體Xj距離不超過小正數的所有個體集合，也稱ε-領域。

系統時滯特性造成穩態工況下參量調整的目標值與現場實際反饋測定值存在較大延時，時間響應與超調量的關系很難衡量而產生隨機信號。這種信號普遍存在于測量中，因此需要信號進行基于最小二乘原理的Savitzky-Golay(S-G)平滑濾波處理，并保存原始信號的形狀和寬度，以此得到真實數據狀態，計算公式如式(3)所示：

(3)

式中:Xj′為濾波后數據；Xj+1為原始測量數據；ci為濾波系數；N為滑動窗口數據個數2m+1；m為窗口寬度。

以天然氣溫度為例計算異常值剔除與平滑濾波前后信號變化情況，如圖2所示。其中上圖表示原始數據，下圖表示預處理后的數據。

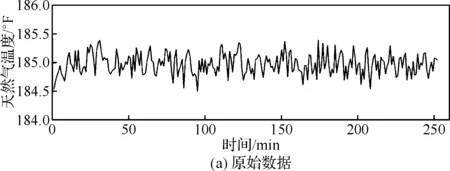
圖2 預處理前后數據對比結果

建模所需31個變量為：燃氣輪機負荷(DW)、壓氣機排氣壓力(Cp)、IGV角度(Cs)、氣體燃料進氣壓力(Fpg1)、氣體燃料閥間壓力(Fpg2)、氣體燃料溫度(Ftg)、燃燒脈動F1～F18、壓氣機入口溫度(tti)、壓氣機排氣溫度(ttd)、壓氣機壓比(Cr)、環境溫度(tati)、排氣溫度(txxtm)、天然氣流量(Fqg)、NOx濃度(Ppm)。將所列變量進行數據量化至[0,1]區間，去除單位限制，須要說明的是在一段時間內由于燃料流量一直保持不變，所以在建模時，將該變量剔除。

2.2 輸入變量特征選擇

偏互信息是在互信息(mutual information，MI)基礎上改進而來的特征選擇方法，它通過消除已選輸入集下待選變量的條件期望值，剔除已選變量集影響的待選變量的殘差，以此消除因子間的相關性對互信息的影響。定義xi為輸入因子，z為已選輸入因子集，yi為輸出因子，xi與z之間存在耦合關聯，則xi與yi之間的偏互信息計算公式如(4)至(6)所示：

(4)

xi′=xi-f(xi|z)

(5)

yi′=yi-f(yi|z)

(6)

式中:xi、yi之間的偏互信息用V(xi,yi)表示；f為條件期望函數；xi′、yi′分別為剔除因子z影響之后的殘差，通過赤池信息準則Taic值作為衡量模型復雜度和模型擬合泛化性能的收斂終止條件，當值隨著變量個數增加而不斷減少達到最低點時，篩選出的變量集為最優集合。定義公式如(7)所示：

(7)

式中:ei為已選因子集z的回歸殘差；p為已選變量個數。

決策樹CART以基尼系數Ggini為指標,根據分類后子集Ggini最低為最優分類規則，設計評價函數。計算現有樣本對原始數據樣本集合H的Ggini系數，如式(8)所示：

(8)

式中:pj為數據集中各類別概率；k為樣本類別。

然后計算相應屬性劃分后的Ggini系數，計算公式如式(9)所示：

(9)

式中:H1、H2為樣本劃分的二個子集，基于Ggini原則找到最小Ggini系數對應的切分特征。

LASSO回歸算法對變量特征進行選擇的主要思想是基于參數正則化，通過對系數增加懲罰函數的約束條件，而實現某些回歸系數趨于0的稀疏壓縮，達到“變量選擇”的目的。一般情況下，LASSO回歸算法采用L1范數懲罰，與L2范數相比，特征選擇更嚴格，更能使回歸系數嚴格接近于0，同時避免模型過擬合。其目標函數定義如公式(10)所示：

(10)

式中:β∈Rp×1為回歸系數向量；X∈Rn×p為特征矩陣；y為目標變量；λ為懲罰因子；‖‖為L1-懲罰項。

分別用3種特征選擇算法(PMI、CART、LASSO)對建模輸入特征進行特征選擇并得到重要性排序結果。實驗所得重要性排序由大到小的前5個變量的結果為偏互信息PMI：ttd、Fpg1、txxtm、tati、tti；套索回歸LASSO：txxtm、tati、Cs、F17、DW；決策樹CART：txxtm、tati、ttd、Cs、Fpg1。從排序結果可以看出，采用不同的特征選擇方法對輸入特征進行相關重要性分析得到的結果并不相同。

2.3 深度置信網絡

典型的深度置信網絡(deep belief network，DBN)由多個疊加的受限玻爾茲曼機構成的底層無監督網絡和上層有監督反向網絡組成。受限玻爾茲曼機(restricted boltzmann machine,RBM)的可見層v與隱含層h之間權重全連接，同層無連接，訓練時，前一個RBM輸出作為下一RBM輸入并完成前一層RBM參數θ的粗調，直至訓練到網絡頂層，之后通過頂層邏輯回歸網絡進行誤差反向傳播的參數細調優化，同時頂層網絡接受最后一個RBM的特征輸出，完成網絡預測。圖3為頂層網絡為BP與4個RBM底層網絡構成的DBN拓撲結構。

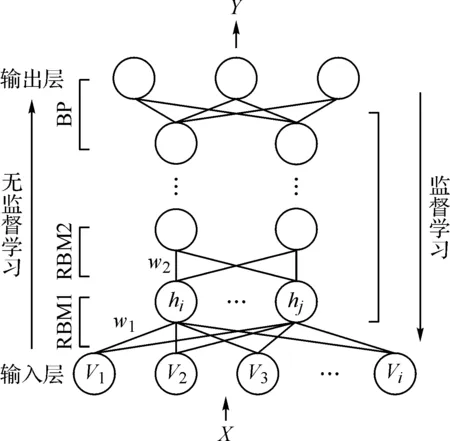
圖3 深度置信網絡結構

其中，單個RBM的能量函數如公式(11)所示：

(11)

式中:ai、bj分別是可見層vi與隱層hj的偏置；wij為可見層vi與隱層hj的連接權重；θ={wij,ai,bj}。由公式(11)可得vi與hj的聯合概率分布如公式(12)所示：

(12)

(13)

式中:Z為—歸一化因子；f為條件期望函數。公式(14)與公式(15)為獨立的vi與hj節點的激活概率：

(14)

(15)

(16)

式中:σ為sigmoid激活函數。

wij、ai、bj更新規則可按照公式(17)～(19)進行更新[16]：

wij=wij+η(fdata(vihj)-frecon(vihj))

(17)

ai=ai+η(fdata(vi)-frecon(vi))

(18)

bj=bj+η(fdata(hj)-frecon(hj))

(19)

式中:η為學習率;fdata為訓練樣本期望;frecon為模型定義期望。本文中η為0.09，frecon為0.06，隱層結構為4層，輸入特征Xi個數為i=10，分別為各自特征選擇算法選擇后的變量，輸出Y為燃氣輪機NOx排放濃度。

2.4 基于深度學習的多特征選擇組合預測算法

單一的特征選擇算法根據自身的評價標準來對表現出不同特征屬性的特征進行選擇，選取的建模輸入最佳子集有所區別，并且單一的特征選擇方法由于算法的局限性所得到的模型精度也是有限的。本文以PMI、CART、LASSO特征選擇算法對同一預測問題進行建模的結果分析，提出了一種MFNDBN方法。算法流程如圖4所示，實施步驟如下。

圖4 建模流程圖

步驟1：基礎建模模型。將原始樣本數據經過數據預處理后分別用PMI、CART、LASSO進行特征選擇并劃分模型預測的訓練、測試集、驗證集Pj={xi,y},i=1,…,N，j=1,2,3。將PMI、CART、LASSO算法下得到的特征重要性評分由大至小的順序進行標簽排序，結合實驗法與專家知識選取各自特征選擇算法前10個特征作為DBN建模輸入X，輸出特征為NOx，然后通過訓練集分別進行DBN建模訓練。

步驟2：非線性組合。根據步驟1訓練的模型得到PMI、CART、LASSO預測模型的測試集與驗證集預測值。假設3種特征選擇建模訓練模型為fp、fc、fl，則第g個樣本的預測值結果分別為y1、y2、y3，將3個模型驗證集和測試集的預測結果重新劃分新的數據集。最后，采用DNN算法將fp、fc、fl模型進行非線性組合，得到最終更精確的MFNDBN預測模型，具體公式如下：

y1=fp(Xp,w1,b1)

(20)

y2=fc(Xc,w2,b2)

(21)

y3=fl(Xl,w3,b3)

(22)

yg=f(y1,y2,y3,w,b)

(23)

式中:yg為以非線性組合方式得到的最終MFNDBN模型NOx排放預測值；Xp、Xc、Xl分別為PMI、CART、LASSO算法選擇的前10個輸入特征；w、b為模型權值與偏置，更新規則如公式(17)～(19)。

3 實驗結果與分析

本研究數據來自某燃氣-蒸汽聯合循環電廠燃氣輪機TCS數據采集系統，采集了2021年1月15日 17:12至 21:23時間段內與NOx排放濃度相關的參數特征30個，采樣頻率為1 min，共252組樣本，表1給出了建模實驗數據信息。

表1 實驗數據信息

3.1 評價指標

為了比較驗證各算法的性能，將平均絕對誤差(Mmae)、平均相對誤差(Mmape)、均方根誤差(Mrmse)、相關系數(R2)4個評價指標作為標準，具體公式如(24)～(27)所示。

(24)

(25)

(26)

(27)

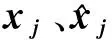
3.2 結果分析

3.2.1 DBN建模預測效果分析

圖5為采用相同LASSO特征選擇算法下不同建模模型(DBN、BP、SVR)的NOx排放預測結果的相對誤差箱型圖。其中，對比建模模型分別為BP算法與SVR算法。從線型圖可以明顯看出，深度網絡DBN的預測能力比其他傳統淺層機器學習算法BP與SVR更好，預測值相對誤差上下四分位數更接近0附近。

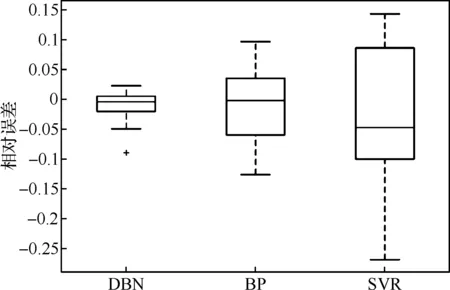
圖5 不同建模模型預測結果

3.2.2 組合特性選擇建模預測效果分析

為了驗證MFNDBN方法性能，與PMI、CART、LASSO三種特征選擇算法進行比較，為不失一般性，均采樣DBN作為建模模型。圖6為各方法在驗證集下的預測值折線圖。

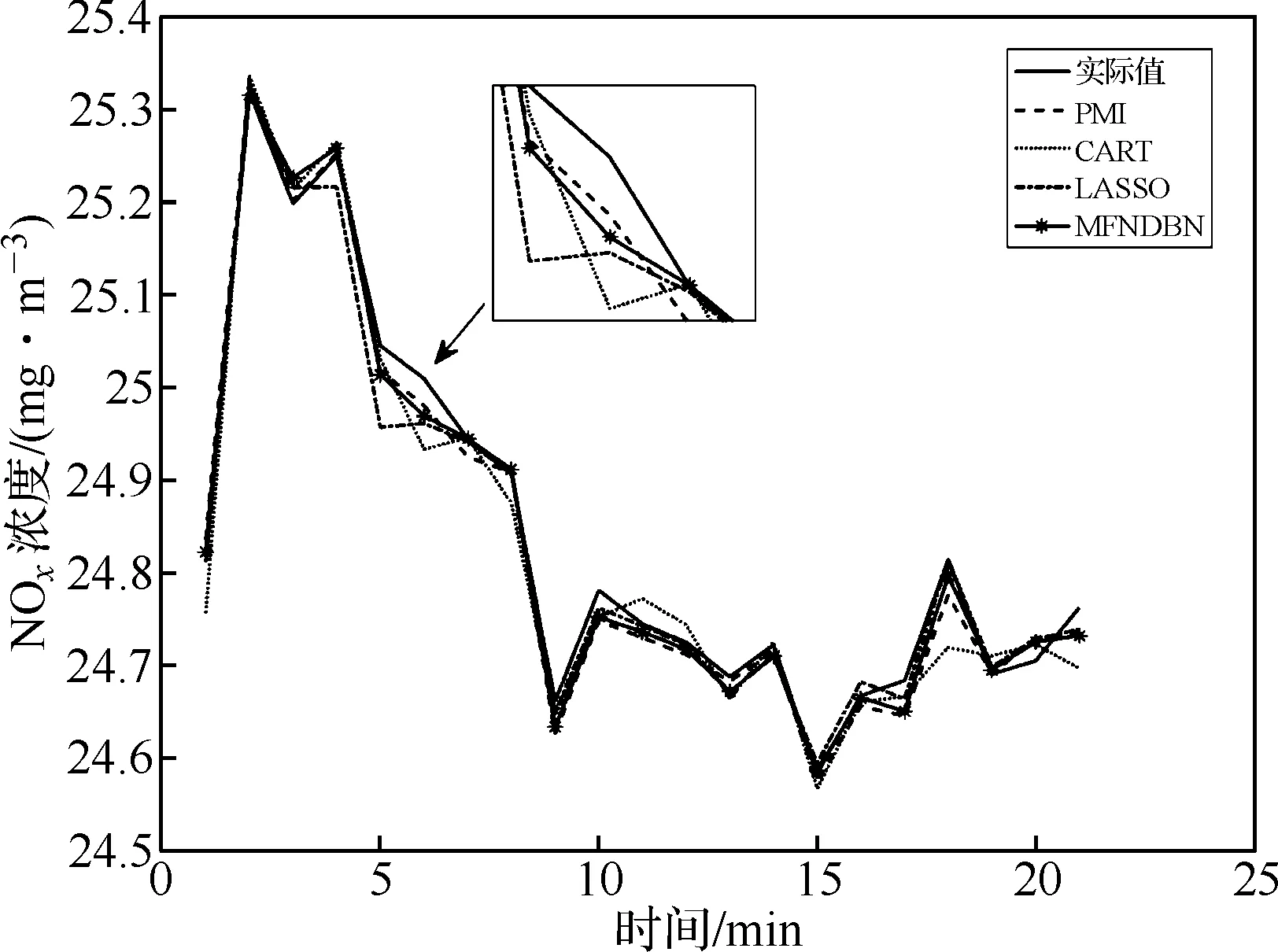
圖6 不同算法預測結果

從圖中可以看出三種特征選擇算法與經過非線性組合預測的特性選擇算法均對實際NOx排放有很高的預測能力，但組合方法更能真實反映排放量的變化趨勢。表2為各算法評價指標對比。

從表2可以看出MFNDBN算法的三種指標值均比其他算法有所提高，采用MFNDBN算法比次優的PMI算法的Mmape、Mrmse、Mmae精度分別提高了10%、4.76%、11.76%，擬合效果R2提高了0.1%，說明MFNDBN算法達到了提高特征選擇精度的要求，算法適用。

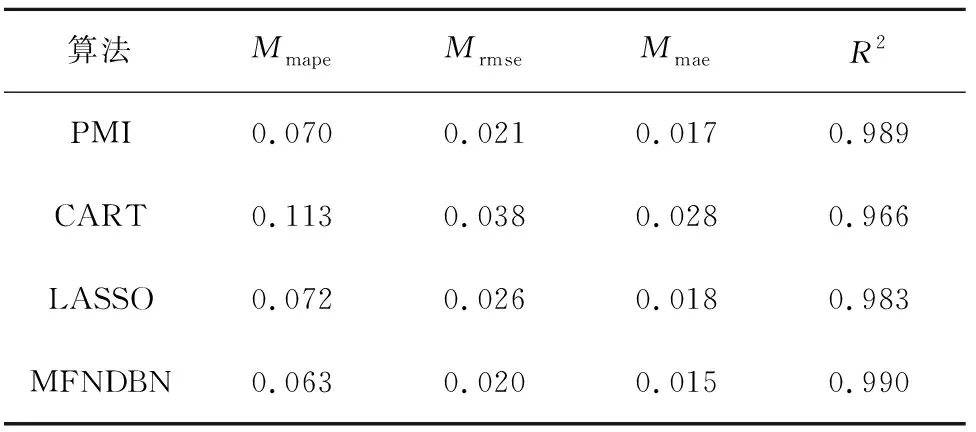
表2 不同算法評價指標結果

圖7中(a)、(b)、(c)、(d)表示的是3種特征選擇算法與MFNDBN方法對比的NOx排放預測值擬合實際測量值的散點圖對比。其中黑色星號代表擬合分布；黑色實對角線為理想分布線；R2代表測量值擬合預測值的程度，值越大，模型預測精度越高。

(a) PMI預測結果

從圖7可以看出圖7(d)的R2值最大并且預測值均勻地集中在理想曲線附近，實驗結果說明所提算法能提高模型的預測精度。

4 結論

燃氣-蒸汽聯合循環機組的燃燒過程是復雜的物理過程，而燃氣輪機NOx排放濃度能夠反映燃氣輪機的燃燒健康水平，是建立燃燒調整模型的重要變量，NOx濃度作為燃氣輪機運行的一個狀態參數耦合其他多參數，導致建立的模型很難實現準確的預測。針對這一問題，提出了一種基于PMI、CART、LASSO算法的多特征組合選擇算法。實驗從數據預處理、特征選取以及建模模型方面進行研究，基于燃氣輪機TCS生產數據建模結果分析，所提出的組合特征選擇算法能夠提高單一特征選擇下的建模模型預測精度。