Rosenau-KdV方程初邊值問題的一個高精度線性守恒差分格式

李貴川, 張芝源, 胡勁松, 章皓洲

(1.西華大學土木建筑與環境學院， 成都 610039； 2.西華大學理學院， 成都 610039； 3.四川大學數學學院， 成都 610064)

1 Introduction

In the study of the dynamics of compact discrete systems, wave-wave and wave-wall interactions cannot be described by the well known KdV equation. To overcome this shortcoming of KdV equation, Rosenau proposed the following Rosenau equation[1,2]

ut+uxxxxt+ux+uux=0

(1)

The existence and uniqueness of solution of (1) were proved by Park[3]. As the further consideration of nonlinear wave,Zuo[4]added a viscous termuxxxto (1) and discussed the Rosenau-KdV equation

ut+uxxxxt+ux+uux+uxxx=0,x∈R,t>0

(2)

Accordingly, the solitary wave solution and periodic solution of Rosenau-KdV of (2) are also investigated. As a more general case, Esfahani[5], Razborova and coworkers[6]discussed the solitary solution of the generalized Rosenau-KdV equation with usual power nonlinearity[7]. Moreover, the two invariants quantities of the Rosenau-KDV equation are also presented. In this paper, we consider the follwing initial-boundary value problem of the Rosenau-KdV equation

(3)

As the solitary wave solution of (2) is[5]

(3) is as the same as Cauchy problem of (2) when -xL?0,xR?0. It is easy to verified that (3) satisfies the following conservative laws[5, 6, 8]

(4)

(5)

whereQ(0) andE(0) are constants depend only on initial data.

It is difficult to obtain the analytic solution of a Rosenau-KDV equation, thus many studies consider the numerical methods. Since the Rosenau-KDV equation is a conservative physical system, numerical schemes with conservation properties are particularly necessary. As Li and Vu-Quoc[9]pointed, in some areas, the ability to preserve some invariant properties of the original differential equation is a criterion to judge the success of a numerical simulation. Similarly, Zhang and coworkers[10]show thata conservative difference scheme can simulate the conservative law of initial problem well and avoid the nonlinear blow-up. Hu and coworkers[8]proposed a three-level linear conservative difference scheme for (3) with theoretical accuracy isO(τ2+h2).Wongsaijai and Poochinapan[11]proposed a three-level average finite difference scheme by coupling the Rosenau-KdV and the Rosenau-RLW equations. A three-level average implicit finite difference scheme is proposed by Mohebbi and Faraz[12]and stability and convergence ofO(τ2+h2) are proved. Using cubic B-spline functions, Ucar and coworkers[13]discussed a Galerkin finite element method. Based on subdomain method, Karakoc and Ak[14]use sextic B-spline functions to simulate the motion of single solitary wave and derive the numerical solution of the Rosenau-KdV equation. Meanwhile, the invariants of motion verify the conservation properties. Kutluay and coworkers[15]studied the operator time-splitting techniques combined with quantic B-spline collocation method for the generalized Rosenau-KdV equation in which conservative properties of the discrete mass and energy are considered.

On the other hand, most second order accuracy schemes are not satisfactory in practical computations, in particular due to the large time scale. Hence, in this paper, by using the Richardson extrapolation technique[16], we propose a three-level linear difference scheme with theoretic accuracy ofO(τ2+h4) and without refined mesh. Furthermore, the proposed scheme can simulate the two conservative laws (4) and (5) well. Mean while, some numerical analysis such as the prior estimate, the existence and uniqueness of the difference solution, the convergence and stability of the scheme are studied.

The rest of this paper is organized as follows. The conservative difference scheme is proposed in Section 2. The existence and uniqueness of numerical solutions are proved in Section 3. Section 4 is devoted to the prior estimate, convergence and stability of the difference scheme. InSection 5, we verify our theoretical analysis by numerical examples.

2 The difference scheme

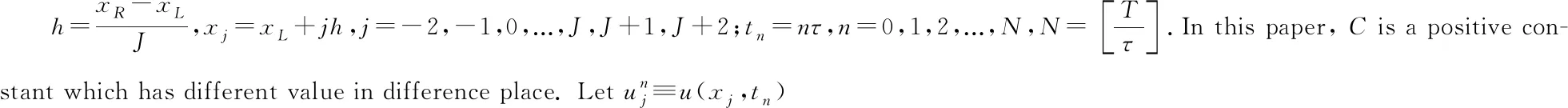
Define

UJ+1=UJ+2=0,j=-2,-1,0,1,...,J,

J+1,J+2}

and

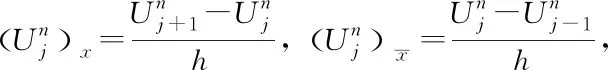
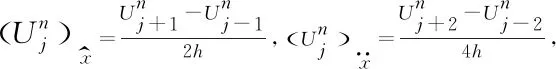
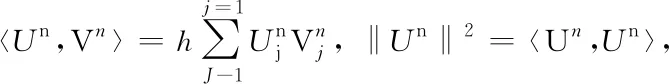
Consider the following difference scheme for (3):

j=1,2,...,J-1;n=1,2,...,N-1

(6)

(7)

(8)

(9)

The discrete boundary condition (9) is reasonable from the homogeneous boundary condition in (3). Define the following two bilinear functions:

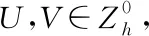
Therefore,

-〈Ux,Ux〉=-‖Ux‖2

(10)

The following theorem shows how the difference scheme (6)～(9) simulates the conservative law numerically.

Theorem2.3The difference scheme (6)～(9) is conservative for discrete energy, that is

(11)

(12)

ProofMultiplyinghon both sides of (6) and taking summation ofj, we obtain from (9) and Lemma 2.1 that

(13)

On the other hand,

Substituting them into (13), we obtain (11) by deducing.

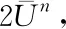
(14)

Note that

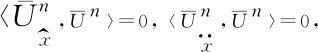
and

So one can obtain by taking them into (14) that

(15)

By the definition ofEn, we obtain (12) by deducing (15) aboutn.

3 Solvability of the difference scheme

Theorem3.1The difference scheme (6)～(9) is uniquely solvable.

ProofWe will use the mathematical induction to prove the result. It is easy to see thatU0andU1are determined uniquely by (7) and (8), respectively. LetU0,U1,…,Un-1,Un(n≤N-1) be the unique solution of difference scheme (6)～(9). Now we considerUn+1in (6). We have

(16)

Taking the inner product of (16) withUn+1, it follows from the boundary condition (9) and Lemma 2.1 that

(17)

Noticing that

〈ψ(Un,Un+1),Un+1〉=

and

〈ξ(Un,Un+1),Un+1〉=

by substituting above results into (17), we get

Then, from Lemma 2.2, we have

that is to say,

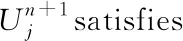
In this seetion we study the convergence and stability of the difference scheme (6)～(9) by using the discrete functional analysis method. The truncation error of the difference scheme (6)～(9) is defined as follows.

j=1,2,...,J-1;n=1,2,...,N-1

(18)

(19)

(20)

(21)

Suppose that the solution of (3) is smooth sufficiently.By using the Taylor expansion, we know that

(22)

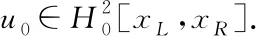
‖u‖L2≤C,‖ux‖L2≤C,‖uxx‖L2≤C,

‖u‖L∞≤C,‖ux‖L∞≤C.

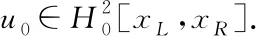
ProofFrom Lemma 2.2 we have

It follows from Theorem 2.3 that

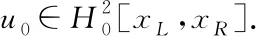
ProofSubtracting (6)～(9) from (18)～(21), we get

j=1,2,...,J-1,n=1,2,...,N-1

(23)

(24)

j=1,2,...,J-1

(25)

(26)

Taking the inner product on both sides of (24) withe1, we obtain from boundary condition (23) and Lemma 2.1 that

From Lemma 2.2, we have

(27)

Again, from (22) the Cauchy-Schwarz inequality and (27), one concludes that

(28)

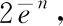
(29)

Similar to (14), we get

(30)

From Lemma 4.1, Theorem 4.2, Lemma 2.2 and the Cauchy-Schwarz inequality, we have

C(‖en+1‖2+‖en‖2+‖en-1‖2+

(31)

C(‖en+1‖2+‖en‖2+‖en-1‖2+

(32)

and

‖en+1‖2+‖en-1‖2

(33)

Substituting (30)～(33) into (29), one gets

C(‖en+1‖2+‖en‖2+‖en-1‖2+

(34)

Similarly, we have

(35)

As a result, (34) can be rewritten into

C(‖en+1‖2+‖en‖2+‖en-1‖2+

(36)

Let

Multiplying 2τon both sides of (36) and taking summation from 1 ton, we get

(37)

From (22), we have

T·(τ2+h4)2.

On the other hand, it follows from (24) and (28) thatB0=O(τ2+h4)2.Similar to the proof of Theorem 4.2, we have

It follows from inequality (37) that

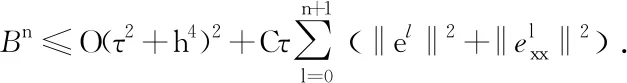
We can prove the following theorem in a similar way of Theorem 4.3.

Theorem4.4Under the hypotheses of Theorem 4.3, {Un} is stable in the sense of norm ‖·‖∞.

5 Numerical examples

For some different value ofτandh, we list errors at several time in Tab.1 and verify the accuracy of the difference scheme in Tab.2. The numerical simulation of two conservative quantities (4) and (5) is listed in Tab.3. The stability and convergence of the scheme are verified by these numerical examples. It shows that our proposed scheme is effective and reliable.

Tab.1 The error estimates of the numerical solution at different time

Tab.2 The numerical verification of the theoretical accuracy O(τ2+h4)

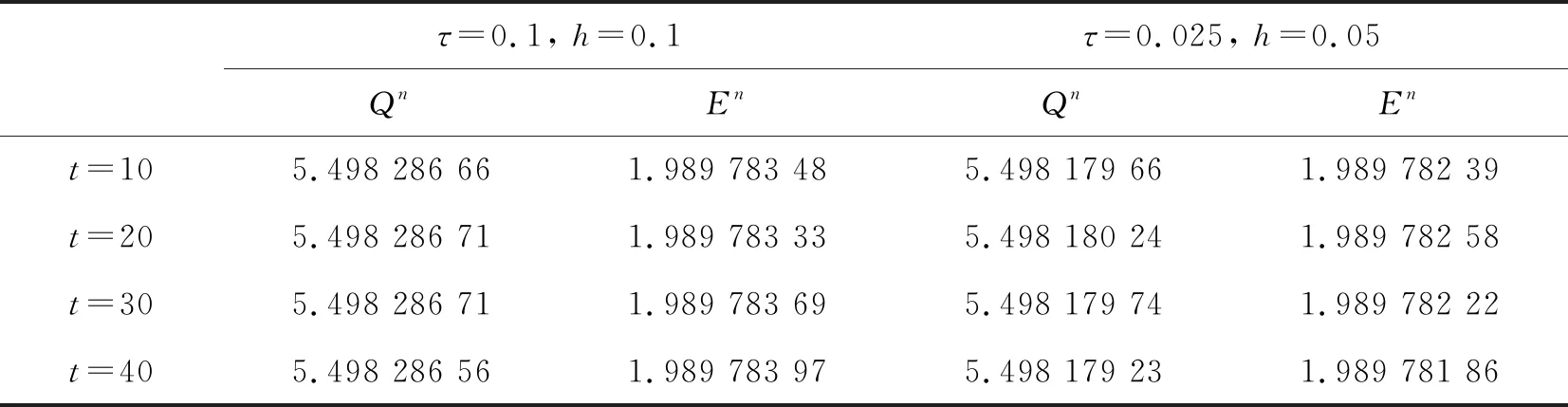
Tab.3 The numerical conservative quantities Qn and En

6 Conclusions

The purpose of this paper is to study the conservative difference scheme for the initial-boundary value problem of Rosenau-KDV equation. By using the Richardson extrapolation, this scheme can improve the spatial accuracy to the fourth order. At the same time, due to the three-layer framework, the scheme does not require any nonlinear iteration, and thus greatly improves the computational efficiency. Theoretically, the energy stability, existence and uniqueness of the numerical solution are given, and the convergence and stability of the numerical scheme are also proved. Finally, numerical examples also verify the theoretical analysis of the proposed scheme.