一類一階常微分系統(tǒng)周期邊值問題正解的存在唯一性
何 婷
(西安電子科技大學數(shù)學與統(tǒng)計學院, 西安 710126)
1 引 言
本文研究如下一階常微分系統(tǒng)

(1)
的周期邊值問題的正解的的存在唯一性,其中a,b:[0,1]→[0,∞)連續(xù)且在[0,1]的任何子區(qū)間上不恒為0,f,g:R→R連續(xù),f(0)≥0,g(0)≥0,且f(t),g(t)關(guān)于t∈[0,∞)是單調(diào)遞增的.
近年來,一階常微分方程(組)正解的存在性得到了廣泛研究[1-9].其中,2001年Zhang 等[7]運用 Krasnoselskii 不動點定理,在一定條件下得到了問題
y′(t)=-a(t)y(t)+λh(t)f(y(t-τ(t)))
(2)
正周期解的存在性.其中a(t),h(t),τ(t)是連續(xù)的T-周期函數(shù),a(t),h(t),f(t)非負, 存在t0∈[0,T]使得a(t0)>0.同時, 諸多學者致力于研究相應(yīng)于問題(2)的微分系統(tǒng)[10-12],如2012年Chen等[11]討論了問題
ui′(t)=-ai(t)ui(t)+
λbi(t)fi(u),i=1,2,...,n
(3)
正周期解的存在性,其中u=(u1,u2,...,un)∈Rn,得到如下結(jié)果:
定理A 設(shè)
(i)ai,bi∈C(R,[0,∞))是ω-周期函數(shù)且



則存在正數(shù)λ*,使得當0<λ<λ*問題時(3)至少存在兩個正周期解;當λ=λ*時問題至少存在一個正周期解;當λ>λ*時問題不存在正周期解.
然而,就我們所知,多數(shù)文獻都只是研究了問題的正周期解的存在性、多解性及不存在性,而少有得到正解的唯一性.一個自然的問題是:什么條件能保證一階常微分系統(tǒng)(1)正解的存在性及唯一性?本文試圖在f于0和∞處超線性(次線性),g于0和∞處次線性(超線性)條件下對研究問題(1)正解的存在性及唯一性進行探討.
本文總假定:
(H1)a,b:[0,1]→[0,∞)連續(xù)且a,b在[0,1]的任何子區(qū)間上不恒為0;
(H2)f,g:R→R連續(xù);
(H3)f(0)≥0,g(0)≥0,f(t),g(t)關(guān)于t∈[0,∞)單調(diào)遞增.
本文的主要結(jié)果如下:
定理1.1設(shè)(H1)~(H3)成立且
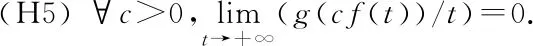
則問題(1)至少有一個正解(u,v)∈(C1[0,1])2.
定理1.2設(shè)(H1)~(H3)成立且
(H6)f(t)在t∈(-∞,0]單調(diào)遞減;

則問題(1)至少有一個正解(u,v)∈(C1[0,1])2.
定理1.3設(shè)(H1)~(H3)成立且
(H9) 存在p,q>0且pq<1使得對任意τ∈(0,1)有f(τt)≥τpf(t)及g(τt)≥τqg(t),t>0.則問題(1)至多有一個正解(u,v)∈(C1[0,1])2.
2 預(yù)備知識
引理2.1[13]設(shè)G1(x,y),G2(x,y)分別為邊值問題
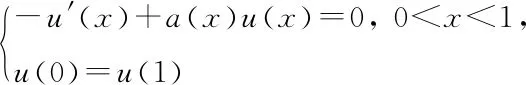
(4)
和
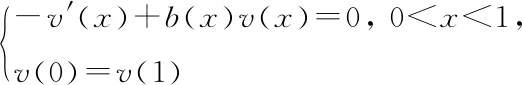
(5)
的格林函數(shù).計算可得
寡日照天氣對設(shè)施內(nèi)輻射、溫度和相對濕度均有影響,其中對輻射的影響要大于對溫度和相對濕度的影響。本研究建立的寡日照條件下番茄生長模型可用于模擬分析不同程度寡日照條件對設(shè)施番茄生長的影響。相對于番茄葉面積指數(shù)和株高,寡日照天氣對生物量的影響程度最為顯著。
易見存在m,M>0,使得
0 引理2.2設(shè)(H1)~(H3)及(H6)~(H7)成立.則存在常數(shù)G>0,使得對于δ∈[0,1],問題 的所有解有 max{‖u‖∞,‖v‖∞}≤G, 證明 由引理2.1,問題(6)等價于如下積分方程組: (7) 設(shè)(u,v)是問題(6)的解.根據(jù)假設(shè)(H3),(H6)和Gi(x,y)>0,i=1,2得u,v≥0.由假設(shè)(H7),存在A>0,使得 (8) 如果‖u‖∞≤A, 則‖v‖∞≤Mf(A).同理,如果‖v‖∞≤A則‖u‖∞≤Mg(A).若‖u‖∞>A,‖v‖∞>A則有 ‖u‖∞≤Mg(‖v‖∞) (9) 和 ‖v‖∞≤Mf(‖u‖∞) (10) 結(jié)合(8)~(10)式可得 所以‖u‖∞>A,‖v‖∞>A不成立.綜上,令 G=max{A,Mf(A),Mg(A)}. 引理得證. Z={u∈C[0,1]:α≤u(x)≤β,x∈[0,1]}. 顯然Z為X的有界閉凸集. 定義算子T:Z→X, Tu(x)= x∈[0,1]. 對于任意u∈Z, Tu(x)= mg(mf(α))≥α. 另一方面,又有 Tu(x)= Mg(Mf(β))≤β. 因此,Tu∈Z.根據(jù)Arzèla-Ascoli定理,T:X→X為全連續(xù)算子.由Schauder 不動點定理,至少存在一個u∈X滿足Tu=u.再令 v(x)∈C1[0,1]滿足 從而u(x)∈C1[0,1]滿足 定理得證. 定理1.2的證明 設(shè)Y=(C[0,1])2,其范數(shù)定義為‖(u,v)‖=max{‖u‖∞,‖v‖∞}.則問題(7)的解等價于積分方程 的解(u,v)∈Y. 定義映射Lδ:Y→Y, 顯然,任意δ∈[0,1],Lδ是緊算子.從而求解問題(1)等價于找映射L1在Y中的一個不動點. 設(shè)BG是Y上的一個球域, BG={(u,v)∈Y:‖(u,v)‖ 根據(jù)引理2.2可知,Lδ在邊界?BG上沒有不動點.令I(lǐng):Y→Y為單位映射.根據(jù)Leray-Schauder度的緊同倫不變性,任意δ∈[0,1],有 deg(I-L1,BG,0)=deg(I-Lδ,BG,0)= deg(I-L0,BG,0)=deg(I,BG,0)=1. 則L1在BG內(nèi)有一個不動點(u,v).結(jié)合Gi(x,y)>0(i=1,2)和假設(shè)(H2),(H3),(H6),(H8),有u(x),v(x)>0,?x∈[0,1].證畢. 定理1.3的證明 設(shè)(uj,vj),j=1,2是問題(1)的兩個正解.定義 Λ={λ∈(0,1]:u1-θu2,v1-θv2≥0, x∈[0,1],θ∈[0,λ]} (11) 顯然,Λ≠?.令τ=supΛ并假設(shè)τ<1.則對于x∈[0,1]有 u1(x)-τu2(x)≥0,v1(x)-τv2(x)≥0. 由式(3)和假設(shè)(H2), (H9), 對于任意x∈[0,1]有 同理有v1(x)≥τpv2(x),x∈[0,1].進而有 -(u1(x)-τu2(x))′+a(x)(u1(x)-τu2(x))= g(v1(x))-τg(v2(x))≥(τpq-τ)g(v2(x)) 和 -(v1(x)-τv2(x))′+b(x)(v1(x)-τv2(x))= f(u1(x))-τf(u2(x))≥ (τpq-τ)f(u2(x)). 若對任意x∈(0,1)有f(u2(x))≡0,g(v2(x))≡0,那么這與u2(x),v2(x)是問題(1)的正解矛盾.從而一定存在x1,x2∈(0,1)滿足f(u2(x1))>0,g(v2(x2))>0.又因為τpq-τ>0可以推出任意x∈(0,1), u1(x)-τu2(x)≥0,v1(x)-τv2(x)≥0, 則存在μ>λ使得μ∈Λ.這與τ=supΛ矛盾.因此,τ=1,且對于任意x∈[0,1], u1(x)-u2(x)≥0,v1(x)-v2(x)≥0. 同理,對于任意x∈[0,1],有 u1(x)-u2(x)≤0,v1(x)-v2(x)≤0. 從而u1=u2,v1=v2.定理得證. 當問題(1)變?yōu)?/p> 時,同樣也可以得到問題正解的存在性及唯一性,即下面的條件結(jié)果. 假設(shè) (H1′)a,b:[0,1]→[0,∞)連續(xù)且a,b在[0,1]的任何子區(qū)間上不恒為0; (H2′)f,g:[0,1]×R→R連續(xù); (H3 ′) 對于任意x∈[0,1],f(x,0),g(x,0)≥0,且f(x,t),g(x,t)關(guān)于t∈[0,∞)單調(diào)遞增. 定義 及 定理4.1設(shè)(H1′)~(H3′)成立且 則問題(12)至少有一個正解(u,v)∈(C1[0,1])2. 定理4.2設(shè)(H1′)~(H3′)成立且 (H6′) 對于任意的x∈[0,1],f(x,t)在t∈(-∞,0]單調(diào)遞減的; (H8′) 存在x,y∈[0,1],f(x,0)>0且g(y,t)>0,t>0. 則問題(12)至少有一個正解(u,v)∈(C1[0,1])2. 定理4.3設(shè)(H1′)~(H3′)成立且 (H9′) 存在p,q>0且pq<1使得對任意τ∈(0,1)有f(x,τt)≥τpf(x,t)及 g(x,τt)≥τqg(x,t),t>0,x∈[0,1]. 則問題(12)至多有一個正解(u,v)∈(C1[0,1])2. 定理4.1的證明 定義算子T′:Z→X, T′u(x)= x∈[0,1]. 對于任意u∈Z,有 mk(mh(α))≥α. 另一方面,有 MG(MF(β))≤β. 后面的證明與定理1.1的證明過程一樣,略.證畢. 定理4.2和定理4.3的證明分別與定理1.2和定理1.3的證明過程類似. 考慮方程組 其中0 容易驗證假設(shè)(H1)~(H3)成立.此外,?c>0,有 從而假設(shè)(H4)成立,同理,假設(shè)(H5)成立.另外,當τ∈(0,1)時,有 同理,當τ∈(0,1)時有g(shù)(τv)>τpg(v).假設(shè)(H9)成立.因此,結(jié)合定理1.1和定理1.3,問題存在唯一正解(u,v)∈(C1[0,1])2.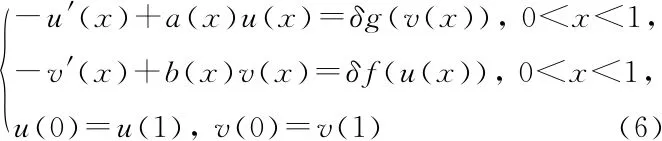



3 主要結(jié)果的證明









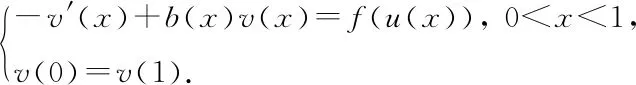








4 主要定理的推廣

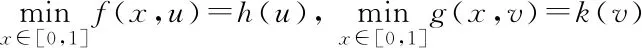

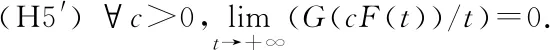
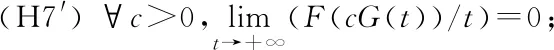









5 應(yīng) 用

