基于復雜網絡的三維CAD裝配模型模塊單元發(fā)掘

韓周鵬 劉 永 巴 黎 史慧帆西安理工大學機械與精密儀器工程學院，西安，710048

0 引言

隨著計算機輔助設計(CAD)系統(tǒng)在工業(yè)界的廣泛應用，企業(yè)積累了大量的三維CAD裝配模型，它們是企業(yè)新產品開發(fā)時可借鑒、可重用的重要知識資源[1]。相對于零件模型，三維裝配模型蘊含有豐富的設計信息，通過零件裝配所體現(xiàn)的結構信息，不僅體現(xiàn)了設計者的設計意圖、設計經驗等知識，也能更好地與用戶需求、產品功能、產品設計方案等問題對應和銜接。在借助CAD系統(tǒng)進行復雜機械產品結構設計過程中，設計者通常是根據(jù)產品功能、性能、參數(shù)等需求，進行產品三維CAD模型的結構設計的。產品原有設計者在產品設計過程中的設計意圖、設計公理、功能、關鍵結構、模塊結構等知識不能通過三維CAD裝配模型直接體現(xiàn)[2]，導致企業(yè)設計經驗不足或缺少原有產品知識儲備的設計者較難理解、重用原有三維CAD裝配模型，特別是對于企業(yè)引入的三維產品模型，模型相關信息可能存在丟失、不完整情況以及設計者自身設計知識與經驗不足，僅僅通過三維裝配模型信息較難理解三維裝配模型的原有設計意圖，進而制約著三維裝配模型重用質量與效率。因此，對復雜機械產品的三維CAD裝配模型進行知識發(fā)掘，捕獲三維裝配模型所蘊含的關鍵零部件、關鍵裝配結構[3]、通用設計結構[4-5]、模塊結構[6]等知識，可以有效還原產品的設計意圖，有助于其他設計者對原有設計知識的理解，啟發(fā)設計者創(chuàng)造性思考，促進產品設計創(chuàng)新[7]。

復雜三維CAD裝配模型作為一種特殊的、蘊含著潛在可重用模塊結構的模型資源，零件數(shù)量繁多且裝配約束關系也相對復雜，所蘊含的具有重用價值的潛在結構知識僅僅通過三維CAD裝配模型難以顯性體現(xiàn)。三維CAD裝配模型的模塊識別可以彌補產品模塊設計意圖缺失、不完整的缺陷。王延平等[8]利用屬性鄰接圖表示三維CAD裝配模型，通過分析零件的拓撲結構、功能、材料相關性建立了零件間的綜合相關度矩陣，給出了面向圖分割的蟻群聚類算法，該聚類算法較為繁瑣，無法定量地評價模塊劃分質量。LI等[9]通過提取CAD裝配模型中裝配約束信息，獲得了零件間的連接關系，然后利用零件間相對自由度來評價零件間的依賴強度，將其表達為設計結構矩陣，通過設計結構矩陣聚類實現(xiàn)了三維CAD裝配模型的模塊劃分，但該方法缺少對零件間功能關系的考慮。

在產品設計階段，通過分析產品設計中零件、部件之間的功能、結構等關聯(lián)關系，將產品劃分為一系列功能獨立的模塊結構以滿足市場不同需求，不僅可以提高產品設計效率，縮短產品設計周期，還可以降低生產與維護管理成本[10]。產品的功能與結構通常為模塊劃分考慮的主要因素[11]。目前已有的模塊劃分方法主要可分為基于圖的模塊劃分[12-13]、基于矩陣的模塊劃分[14-15]和基于智能算法的模塊劃分[16-17]，基本可以滿足產品設計不同階段的個性化需求。

為了能夠從復雜三維CAD裝配模型中獲得易于重用的模塊化結構單元，提高三維CAD裝配模型的重用水平，本文提出一種基于復雜網絡的三維CAD裝配模型模塊單元發(fā)掘方法。本文方法在前期研究工作的基礎上，融合裝配零件的多源關聯(lián)信息綜合評價裝配零件的關聯(lián)強度，構建三維CAD裝配模型的關聯(lián)關系網絡，并借助復雜網絡的社區(qū)發(fā)現(xiàn)思想，設計一種基于CNM(Clauset-Newman-Moore)的三維CAD裝配模型模塊單元發(fā)掘算法，可以自動柔性地發(fā)掘三維裝配模型所蘊含的模塊單元知識。

1 三維CAD裝配模型的關聯(lián)關系網絡

1.1 裝配零件關聯(lián)強度評價

裝配體是指零件按照一定的裝配約束組合在一起，使每個零件在裝配體中具有特定的空間位置及拓撲形式，以滿足產品設計的功能與性能的組合體。復雜機械三維CAD裝配模型可能由多個不同的模塊結構構成，同一模塊的裝配零件之間具有緊密的物理連接關系，并且能夠共同實現(xiàn)產品的某些功能。復雜機械三維CAD裝配模型模塊知識發(fā)掘過程中綜合考慮了零件之間的物理連接、功能關聯(lián)關系及材料相似性關聯(lián)，能夠更加客觀、定量地評價裝配零件之間的關聯(lián)強度[18]。

1.1.1裝配結構關聯(lián)分析

零件之間的連接與配合方式影響著裝配結構的關聯(lián)程度，以零件結構的可拆卸性與穩(wěn)固性作為關聯(lián)依據(jù)進行評價[16]，可實現(xiàn)零件之間裝配結構關聯(lián)強度Is(i，j)的評價，如表1所示。

表1 裝配結構關聯(lián)強度評價準則

1.1.2功能關聯(lián)分析

裝配產品的某一功能可能由一個或多個零件組合共同完成。三維裝配模型模塊知識可以是具有某種或多種功能的裝配結構單元。通過分析零件之間的功能關聯(lián)，可以將功能聯(lián)系比較緊密的零件劃分在同一模塊單元內。零件之間的功能關聯(lián)主要體現(xiàn)在任意兩個裝配零件在完成同一功能時的協(xié)同程度上[16]。例如，軸與鍵一起共同完成傳遞動力的功能時是缺一不可的，一般被認為具有較強的功能關聯(lián)關系。為了有效評價零件之間的功能關聯(lián)強度If(i，j)，給出零件之間的功能關聯(lián)強度評價準則，如表2所示。

表2 功能關聯(lián)強度評價準則

1.1.3材料相似性分析

材料類型影響著零件的設計與制造，材料相同的零件可能會采用相同的制造工藝或制造設備，所構成的裝配結構模塊更有利于制造與維護[8]，因此，材料相似性可以作為三維裝配模型模塊單元發(fā)掘的影響因素之一。材料相似性度Im(i，j)可表達為

(1)

1.1.4綜合關聯(lián)強度評價

從結構、功能、材料三個方面對三維裝配模型中零件之間關聯(lián)關系進行分析，并考慮三維裝配模型中結構、功能、材料在模塊單元中的重要程度，可以將零件之間的綜合關聯(lián)強度I(i，j)表達為

I(i，j)=ω1Is(i，j)+ω2If(i，j)+ω3Im(i，j)

(2)

式中，ω1、ω2、ω3分別為裝配結構關聯(lián)、功能關聯(lián)與材料相似度的權重，且滿足ω1+ω2+ω3=1。

由上可建立綜合關聯(lián)強度矩陣M：

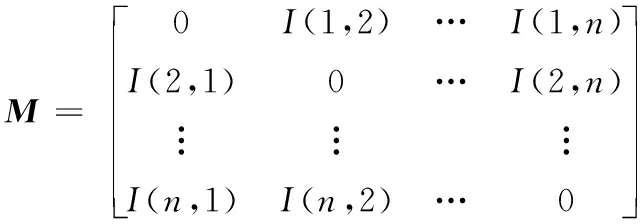
(3)

式中，n為三維裝配模型中裝配零件數(shù)量；M為n×n階對稱矩陣，此矩陣可為三維裝配模型的關聯(lián)關系網絡構建提供輸入。

1.2 三維裝配模型的關聯(lián)關系網絡構建

將三維CAD裝配模型中裝配零件作為網絡節(jié)點，零件之間關聯(lián)關系以網絡邊的形式描述，其本質上可以看作一種復雜網絡系統(tǒng)。依據(jù)裝配零件之間的綜合關聯(lián)矩陣M，運用復雜網絡理論與方法，可以構建成一個無向加權網絡N。裝配零件之間的關聯(lián)關系網絡N可以表示為

N={V，E，W}

(4)

式中，V為關聯(lián)關系網絡N的節(jié)點集合，即裝配零件集；E為該網絡的邊集合，即裝配零件的關聯(lián)關系；W為網絡中邊的權重集合，即綜合關聯(lián)強度。

關聯(lián)關系網絡N作為無向加權網絡，能夠較好地描述三維裝配模型中零件之間的關聯(lián)情況。利用復雜網絡中社區(qū)發(fā)現(xiàn)算法可以對該關聯(lián)關系網絡進行社區(qū)發(fā)現(xiàn)，每個社區(qū)結構代表三維裝配模型中一個子裝配體或模塊單元，進而實現(xiàn)三維裝配模型中模塊單元知識的發(fā)掘。為了方便理解社區(qū)發(fā)現(xiàn)算法，下面將引入鄰接矩陣與模塊度函數(shù)Q兩個概念。

1.2.1鄰接矩陣A

若關聯(lián)關系網絡N具有n個節(jié)點，則對應的鄰接矩陣A的元素可表達為

(5)

式中，ωij表示節(jié)點i與j之間邊的權重，即零件i、j的綜合關聯(lián)強度I(i，j)。

1.2.2模塊度函數(shù)Q

模塊發(fā)掘結果的好壞需要一定的標準衡量，模塊度作為模塊劃分的一個有效指標，可以用來評價三維裝配模型模塊單元發(fā)掘是否合理。模塊度函數(shù)Q是復雜網絡中社區(qū)發(fā)現(xiàn)質量的評價指標，可以用來評價關聯(lián)關系網絡N社區(qū)結構發(fā)現(xiàn)質量。關聯(lián)關系網絡N的模塊度Q[19]可表達為

(6)

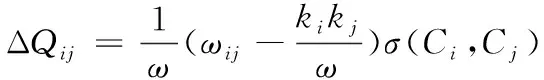
(7)

(8)

(9)

(10)

式中，ω為關聯(lián)關系網絡N所有邊的權重之和；ki為節(jié)點i的所有邊權重之和；Ci、Cj為節(jié)點i、j所在社區(qū)結構；ΔQij為節(jié)點i與j合并時模塊度增加量。

2 基于CNM社區(qū)發(fā)現(xiàn)的三維裝配模型模塊單元發(fā)現(xiàn)算法

以三維裝配模型的關聯(lián)關系網絡模型為基礎，借助復雜網絡的社區(qū)發(fā)現(xiàn)算法，可以發(fā)現(xiàn)關聯(lián)關系網絡中的社區(qū)結構，進而實現(xiàn)三維CAD裝配模型模塊單元知識的發(fā)掘。

Fast Newman社區(qū)發(fā)現(xiàn)算法是一種基于凝聚的貪婪算法[20]，其算法過程是將網絡N看成n個獨立的社區(qū)結構，隨后將n個社區(qū)結構不斷兩兩合并，每次合并選擇模塊度增量最大的新社區(qū)結構，直到社區(qū)合并為一個社區(qū)；最后，根據(jù)模塊度函數(shù)Q(k)(k=1，2，…，n)最大值確定最佳的社區(qū)結構數(shù)量，從而得到該網絡的最佳社區(qū)結構。CNM算法以Fast Newman社區(qū)發(fā)現(xiàn)算法為基礎[21]，采用堆的方式進行計算、更新網絡的模塊度，額外增加3個輔助數(shù)據(jù)結構，包括模塊度增量矩陣、最大堆和輔助向量來提高算法效率，該算法的時間復雜度為O(nlog2n)，其中，n為網絡的節(jié)點總數(shù)。基于改進CNM社區(qū)發(fā)現(xiàn)的三維裝配模型模塊單元發(fā)現(xiàn)算法步驟如下。

輸入：關聯(lián)關系網絡N，鄰接矩陣A；

輸出：C(社區(qū)結構),Q(模塊度函數(shù))；

步驟(1)：初始化網絡N中的n個節(jié)點作為獨立的社區(qū)結構，令模塊度Q=0；

步驟(2)：利用式(8)、式(9)計算網絡N中邊的總權重ω、社區(qū)結構中每個節(jié)點的邊權重之和ki；

步驟(3)：合并具有鄰接關系的任意2個社區(qū)結構，利用式(7)計算對應的模塊度增量矩陣ΔQ；

步驟(4)：從最大堆中選取最大的模塊度增量，將對應的兩社區(qū)合并為一個社區(qū)并更新模塊度矩陣等輔助數(shù)據(jù)結構；利用式(6)計算模塊度函數(shù)Q(k)，k=n-1；

步驟(5)：判斷社區(qū)數(shù)量k，若k=1，執(zhí)行步驟(6)；反之，則執(zhí)行步驟(2)～步驟(4)；

步驟(6)：以模塊度函數(shù)Q(k)的最大值確定最佳的社區(qū)數(shù)量k，輸出對應的社區(qū)結構與三維裝配模型模塊單元。

模塊度本質上為某一社區(qū)結構內的所有邊權重之和減去與該社區(qū)結構相連的邊權重之和，模塊度函數(shù)Q值越大，說明社團結構越明顯。在實際網絡社區(qū)發(fā)現(xiàn)中Q的最大值范圍在0.3～0.7。模塊度函數(shù)值隨社區(qū)發(fā)現(xiàn)數(shù)量而變化，所以通過模塊度函數(shù)可以確定最佳的社區(qū)結構數(shù)量，避免人工的主觀干預。根據(jù)三維裝配模型自身的裝配拓撲結構、功能、材料等關聯(lián)強度來自動實現(xiàn)模塊單元知識的發(fā)掘，更能反映模塊單元的內外規(guī)律與特性。

3 實例分析

以某蝸輪蝸桿減速器三維CAD裝配模型為例，提取該三維CAD裝配模型的裝配關系信息，構建對應的關聯(lián)關系加權網絡模型，利用社區(qū)發(fā)現(xiàn)CNM算法進行蝸輪蝸桿減速器三維CAD裝配模型模塊單元知識發(fā)掘。圖1為某蝸輪蝸桿減速器的三維CAD裝配模型示意圖，表3所示為該裝配模型的零件信息。

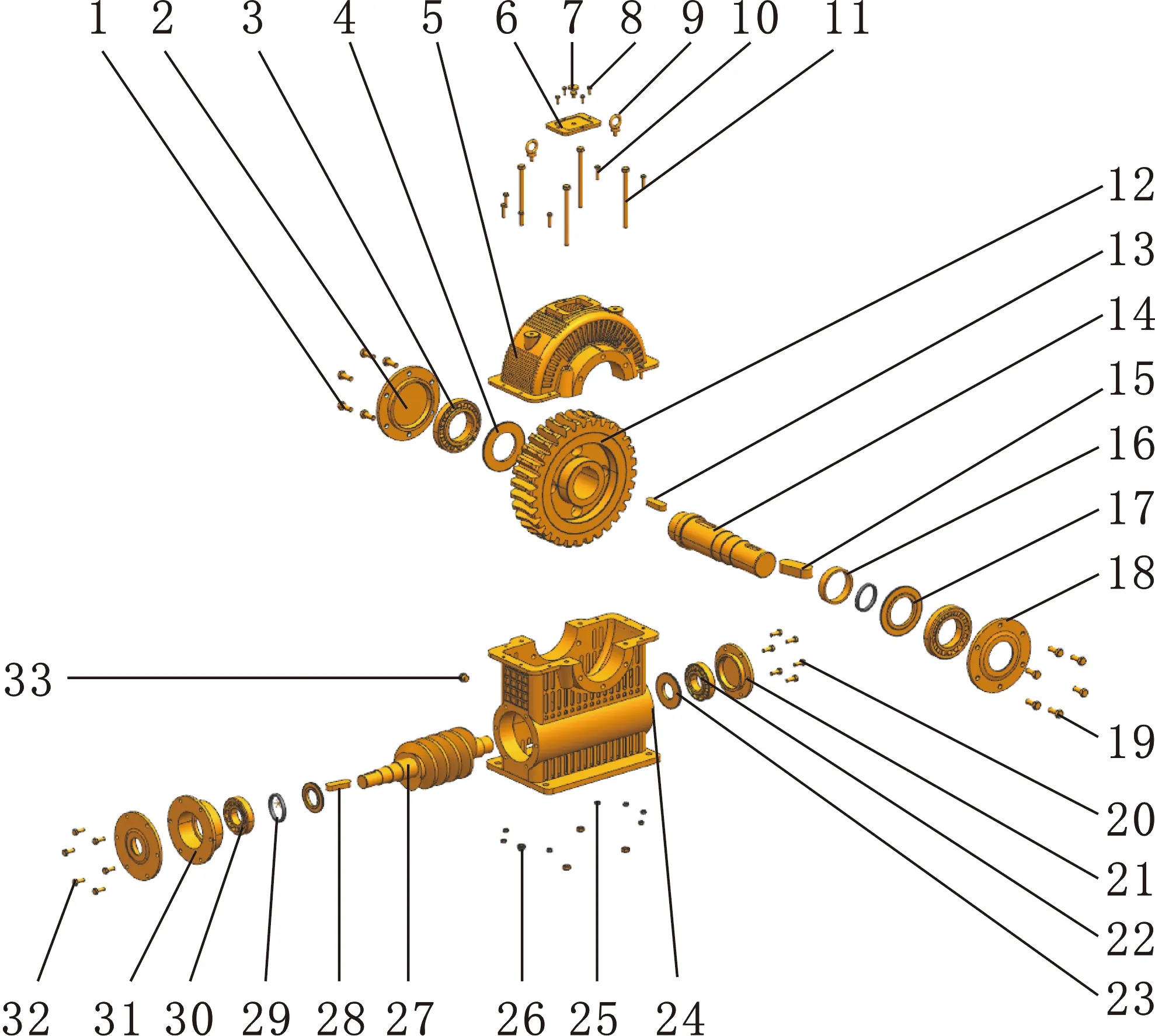
圖1 蝸輪蝸桿減速器三維裝配模型示意圖Fig.1 3D CAD assembly of worm reduction box

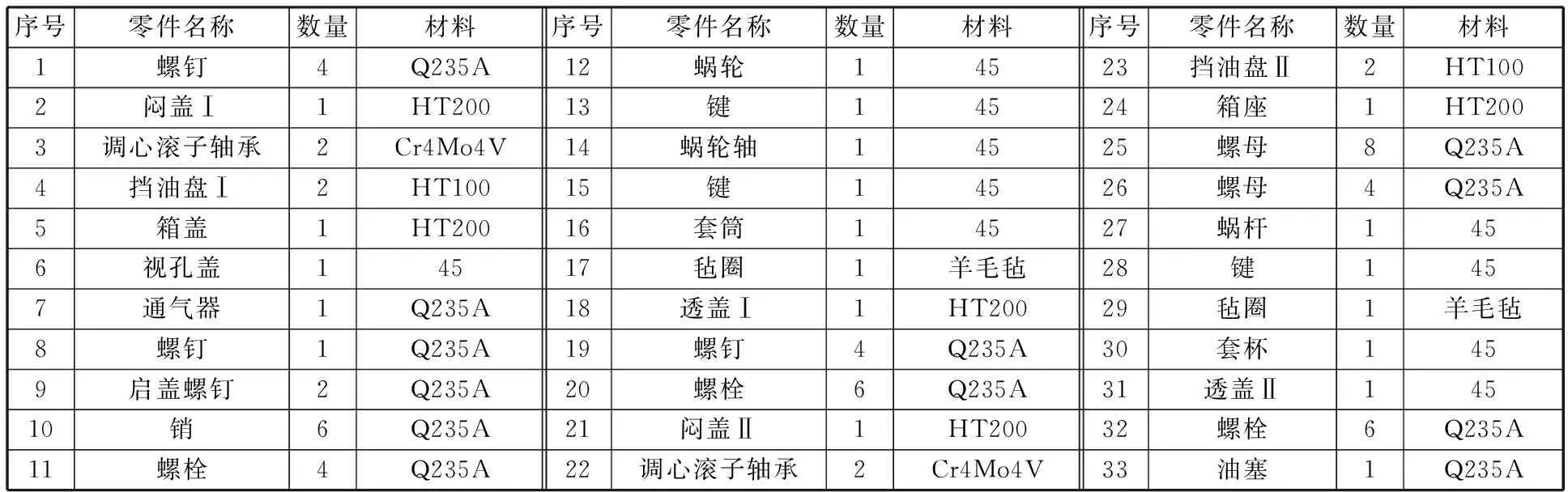
表3 蝸輪蝸桿減速器的零件信息

通過提取蝸輪蝸桿減速器三維CAD裝配模型的裝配約束、零件屬性信息，可獲得零件之間的連接關系信息，如表4所示。

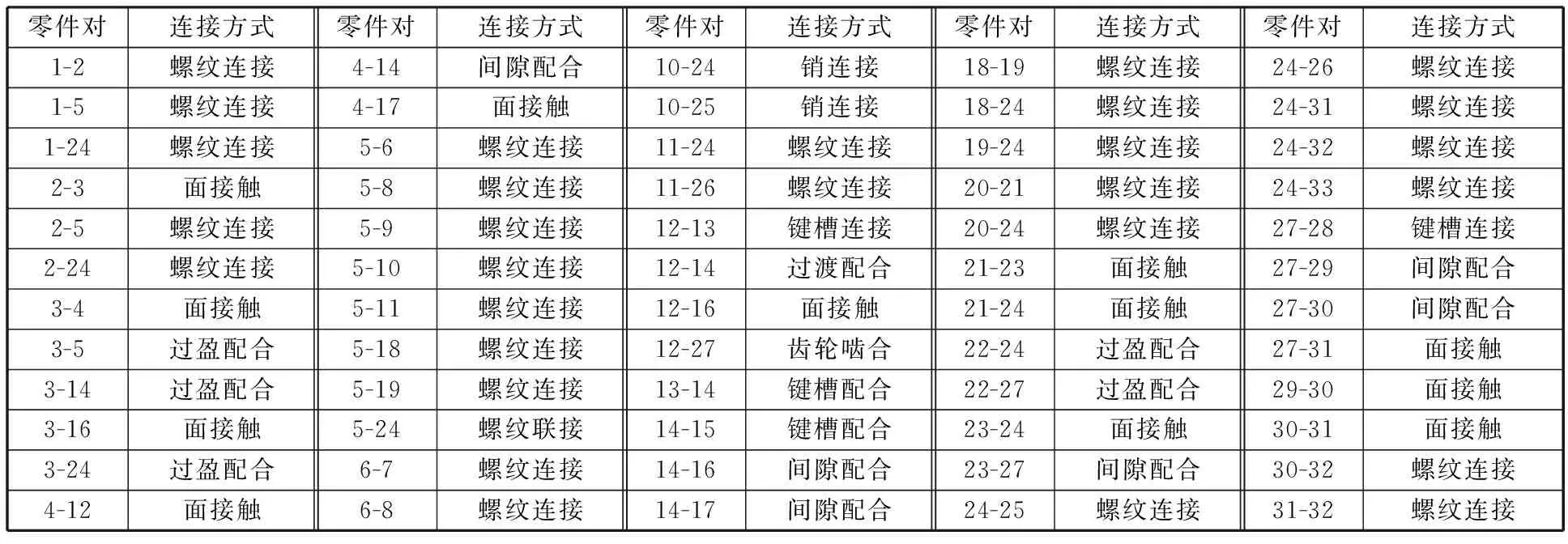
表4 零件連接信息

3.1 零件關聯(lián)強度評價

利用表1、表2、式(3)關聯(lián)強度評價準則可對蝸輪蝸桿減速器三維裝配模型中零件之間結構、功能及材料相似度的關聯(lián)強度進行評價。蝸輪蝸桿減速器通過蝸輪齒輪嚙合主要起到降速、轉換力矩的作用。該三維裝配模型的結構、功能信息對模塊單元知識發(fā)現(xiàn)相對重要，材料可作為輔助參考因素。因此，對該類三維裝配模型模塊單元知識發(fā)掘時，可將結構、功能、材料相似度的權重設置為ω1=0.45，ω2=0.45，ω3=0.1。零件之間的綜合關聯(lián)強度I=0.45Is+0.45If+0.1Im。利用式(2)、式(3)可得到綜合關聯(lián)矩陣，如圖2所示。

3.2 裝配零件之間的關聯(lián)關系網絡

利用1.2節(jié)中關聯(lián)關系網絡構建流程，以綜合關聯(lián)強度矩陣M為基礎，通過Gephi可視化工具建立蝸輪蝸桿減速器三維裝配模型的關聯(lián)關系網絡N，如圖3所示，其中每個節(jié)點編號代表零件序號，節(jié)點邊線性的粗細程度表示邊的權重大小。

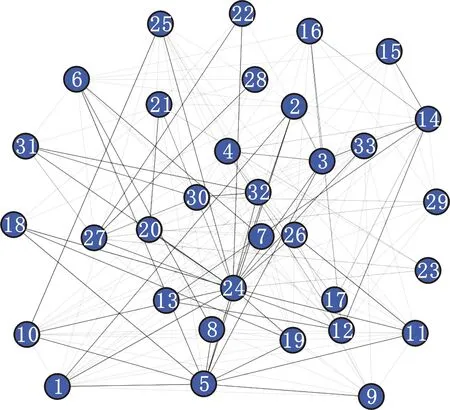
圖3 蝸輪蝸桿減速器的關聯(lián)關系網絡NFig.3 Correlation relationship network N of worm reduction

3.3 模塊單元發(fā)掘

以MATLAB軟件為平臺實現(xiàn)了基于CNM社區(qū)發(fā)現(xiàn)算法編程，可以對蝸輪蝸桿減速器三維裝配模型的零件關聯(lián)關系網絡N進行社區(qū)發(fā)現(xiàn)。社區(qū)發(fā)現(xiàn)過程如圖4所示，其中，圖4a表示關聯(lián)關系網絡N社區(qū)發(fā)現(xiàn)過程；圖4b為CNM社區(qū)發(fā)現(xiàn)的模塊度函數(shù)曲線。由模塊度函數(shù)曲線可知，當社區(qū)結構數(shù)量k=4時，模塊度Q取得最大值0.3642，從而可以確定蝸輪蝸桿減速器三維CAD裝配模型模塊單元發(fā)掘的最佳結果為4個模塊單元，對應的模塊單元零件集合為C1={v10，v11，v20，v21，v23，v24，v25，v26，v33}，C2={v1，v2，v5，v6，v7，v8，v9，v18，v19}，C3={v3，v4，v12，v13，v14，v15，v16，v17，v29}，C4={v22，v27，v28，v30，v31，v32}，模塊單元發(fā)掘的最終結果如表5所示。表5中蝸輪蝸桿三維裝配模型的模塊單元發(fā)現(xiàn)結果，由于在關聯(lián)強度評價時考慮了結構、功能、材料因素，所發(fā)掘的模塊知識在設計-制造-裝配過程中具有較高的實用性，與實際模塊劃分結果也比較吻合。如蝸輪-蝸輪軸模塊，不僅在設計時考慮模塊內零件(O形密封圈、軸套、鍵)的尺寸、參數(shù)信息，而且在制造、裝配環(huán)節(jié)也可作為同一模塊考慮其材料、采購、裝配等指標；模塊單元內所蘊含的設計、制造、裝配相關知識能夠幫助設計人員更好地理解、重用該三維裝配模型。

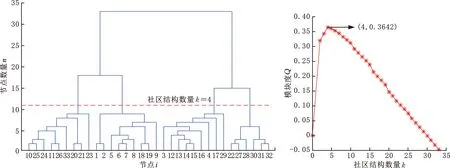
(a)基于CNM的社區(qū)發(fā)現(xiàn)結果 (b)模塊度Q函數(shù)

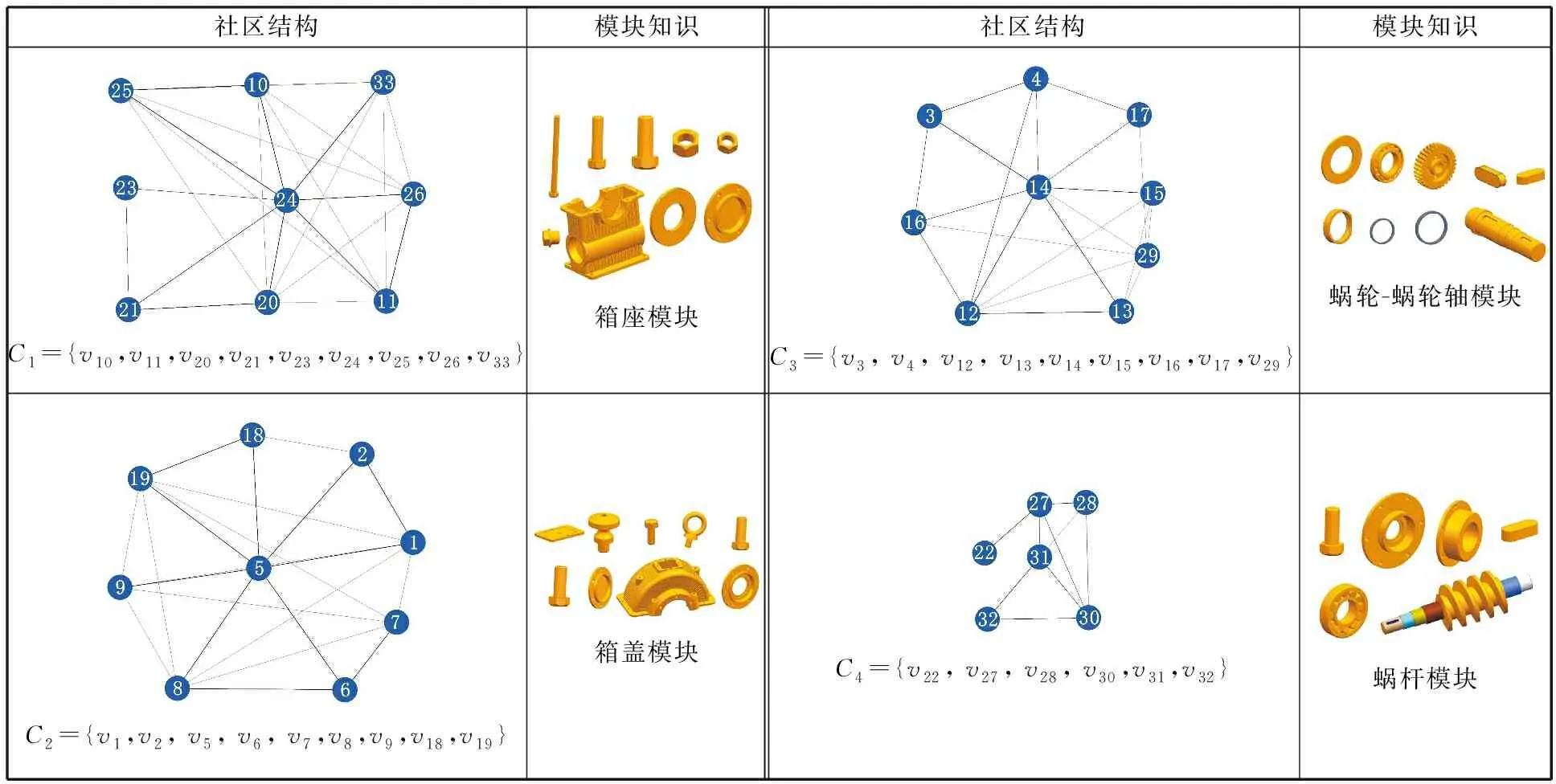
表5 模塊知識發(fā)掘結果

為了進一步分析表2中強度指標與式(2)中權重因子對模塊發(fā)掘結果的影響，分別對關聯(lián)強度指標If與權重ω的數(shù)值調整，權重變化后模塊發(fā)掘結果如表6所示。由表6可知，調整強度指標值If后模塊發(fā)掘結果未變化，而調整權重ω后模塊發(fā)掘結果發(fā)生了變化。強度指標值If對功能關聯(lián)強度評價準則而言僅僅是數(shù)值上的差異，僅僅影響綜合關聯(lián)強度M的相對值，對模塊劃分結果影響不敏感。權重ω則直接影響綜合關聯(lián)強度M，對模塊劃分結果較為敏感。式(2)中權重因子的確定是模塊劃分的關鍵，影響著模塊劃分結果的準確性，因此對于權重ω來說需要主觀歷史經驗與客觀評價兩者綜合考慮來確定，以便能夠更加準確地發(fā)掘三維裝配模型中模塊結構知識。本文權重ω的確定主要由設計者經驗與層次分析法(AHP)來確定。

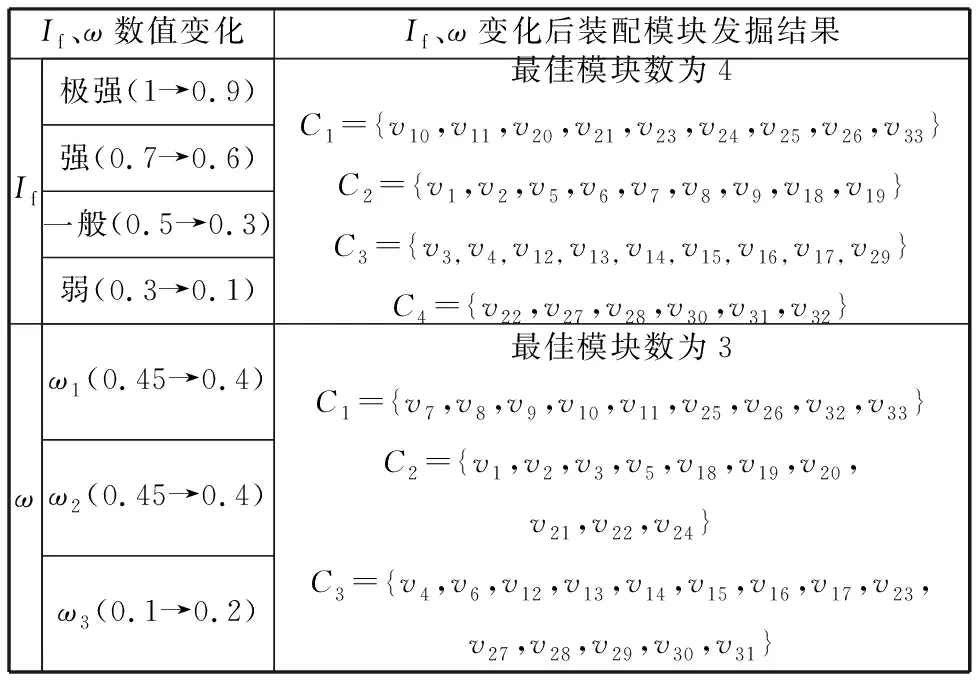
表6 強度指標If與權重ω對模塊發(fā)掘的影響

3.4 方法比較

文獻[18]Fast Newman算法時間復雜度為O((m+n)n)，其中，n為關聯(lián)網絡節(jié)點總數(shù)，m為網絡總邊數(shù)，本文所給算法時間復雜度較之有所降低，執(zhí)行效率較高。文獻[8]蟻群聚類方法將襟翼三維裝配模型劃分為6個模塊，且蟻群算法時間復雜度為O(n2)，其中，n為關聯(lián)關系網絡中節(jié)點總數(shù)量；而通過本文方法發(fā)掘的最佳模塊數(shù)量為3時模塊度函數(shù)取得最大值，表明此時襟翼裝配模型的模塊內部具有更高的內聚度，模塊間有較弱的耦合。兩種方法運行結果對比如圖5所示。

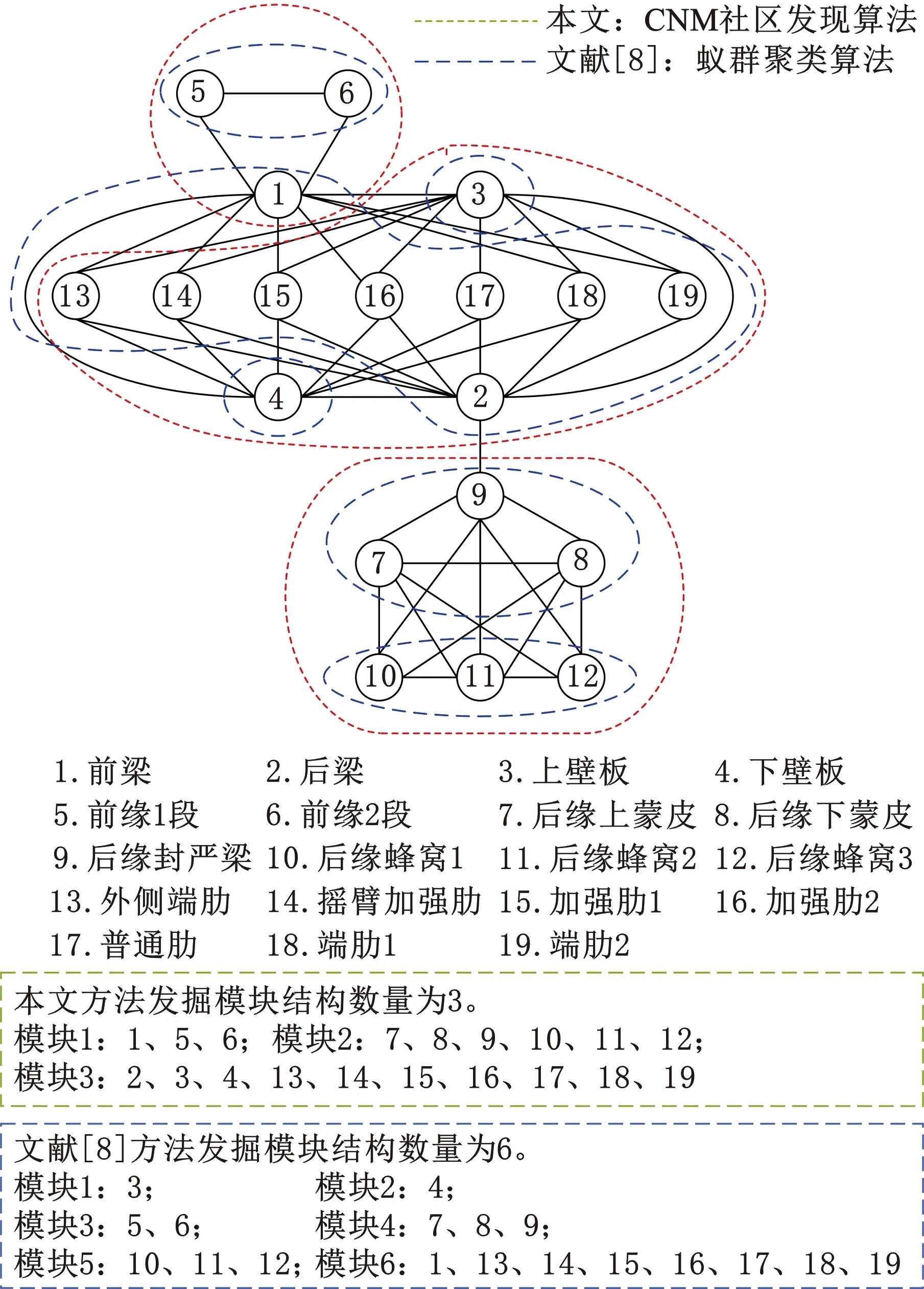
圖5 本文方法與文獻[8]方法對比Fig.5 Comparison between proposed method & reference[8]

為了進一步驗證本文方法的普適性，以文獻[16]中的柱塞泵為對象，利用本文方法對該柱塞泵三維裝配模型模塊單元進行發(fā)掘。該三維裝配模型模塊單元發(fā)掘過程如圖6所示，由圖6可知，柱塞泵三維裝配模型模塊單元發(fā)掘最佳模塊數(shù)量為5，各模塊所包含的零件分別為模塊C1={1，2，17，20，25，40}，C2={3，5，8，14，23，35，37，38，39，41，42}，C3={4，6，11，12，15，16，36}，C4={7，9，10，13，18，19，26，29，30，34，43，44}和C5={21，22，23，24，27，28，31，32，33，39}。該模塊發(fā)掘結果與文獻[16]中模塊劃分結果相比，雖然模塊1和模塊5有部分零件存在差異，但整體來說比較吻合，本文與文獻[16]中實例計算結果對比如表7所示。利用本文方法可以有效地發(fā)掘三維裝配模型中的模塊單元，還原三維產品模型的原有模塊設計信息。

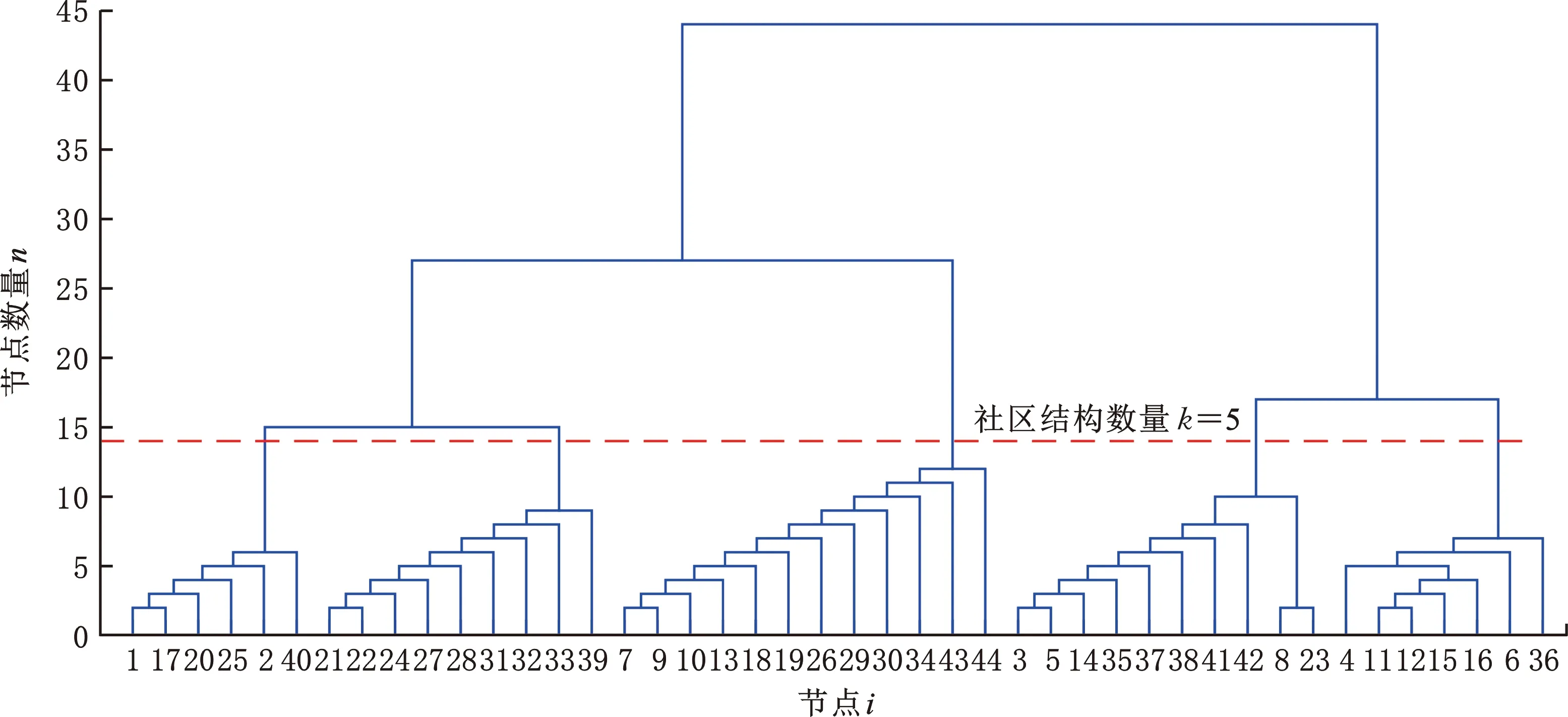
圖6 柱塞泵三維裝配模型模塊單元發(fā)掘過程Fig.6 Modular units knowledge discovering process of 3D assembly model of piston pump

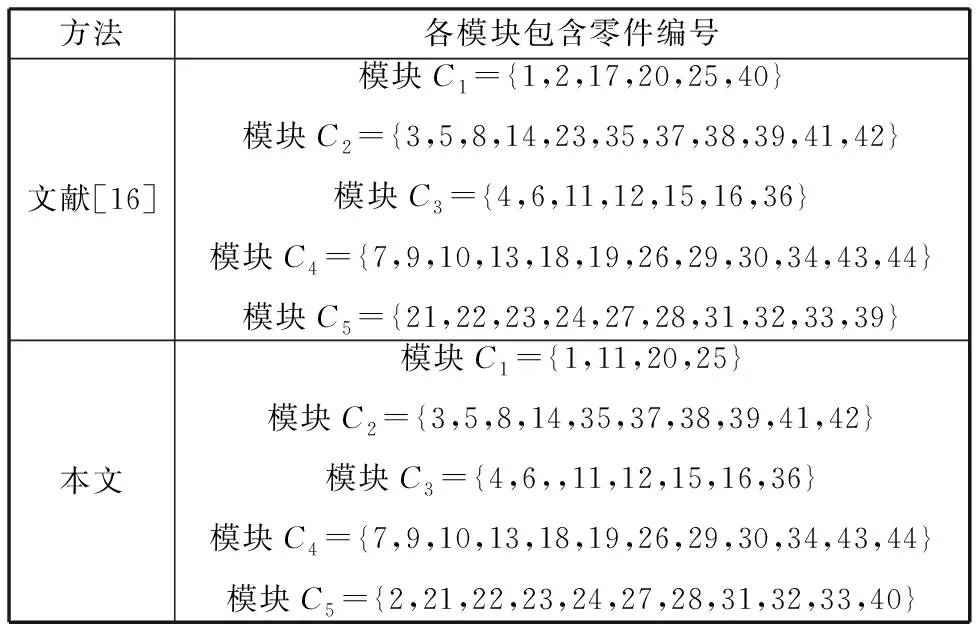
表7 本文方法與文獻[16]中實例計算對比

總體而言，本文方法綜合考慮了零件之間的物理關系、功能關系與材料相似度因素，符合產品設計-制造-裝配過程中的實際操作需求，所提CNM社區(qū)發(fā)現(xiàn)算法易于編程實施，時間復雜度較低，可以滿足設計者在產品設計不同階段中三維裝配模型模塊單元知識發(fā)現(xiàn)與重用需求。

4 結論

(1)融合裝配零件的結構、功能、材料關聯(lián)信息，給出了三維CAD裝配模型零件之間關聯(lián)強度綜合評價方法。

(2)基于復雜網絡構建了三維CAD裝配模型的關聯(lián)關系網絡；提出了一種基于CNM社區(qū)發(fā)現(xiàn)的三維裝配模型模塊單元發(fā)掘方法，該方法編程簡單且易于實施，時間復雜度為O(nlog2n)。

(3)所提方法可以有效地發(fā)掘三維裝配模型所蘊含的高質量模塊單元知識，有助于提高設計者對三維裝配模型模塊知識的理解和重用水平。